Morh-Coulomb近接交叉隧道围岩塑形叠加区分析

贾宝新，姜　明，赵　培，贾志波

(1.辽宁工程技术大学　土木与与交通学院，辽宁　阜新　123000；2.中国地震局地质研究所，北京　100000)



Morh-Coulomb近接交叉隧道围岩塑形叠加区分析

贾宝新1,2，姜明1，赵培1，贾志波1

(1.辽宁工程技术大学土木与与交通学院，辽宁阜新123000；2.中国地震局地质研究所，北京100000)

摘要：为定量确定交叉隧道相邻硐室塑性叠加区域半径, 并分析其对交叉隧道围岩稳定性的影响, 以工程力学中应用最广的Morh-Coulomb强度准则为依据，经理论推导，得到了在上下隧道小净距影响下的塑性区范围及其相应解析解。并在此基础上对影响近接围岩稳定性的因素进行了探讨。 结果表明交叉隧道塑性区叠加半径大小与内聚力、支护抗力、内摩擦角、原岩应力、近接距离等因素相关。通过Morh-Coulomb强度方程计算出的结果与实测数据对照，结果相吻合，表明本文提出的塑性区计算公式能较好地反映出交叉隧道围岩的稳定性情况。

关键词：隧道工程，围岩稳定；Morh-Coulomb准则；交叉隧道；小净距；塑性叠加区

0引言

目前，隧道、边坡、桥梁等岩土工程的围岩稳定性分析中，岩体的塑性区半径的计算有着举足轻重的作用，并且模型试验、现场测试和理论分析中都给出了塑性区范围的求解方法。现场可采用围岩钻孔窥探[1]对塑性范围进行测量，但利用窥探试验来获取硐室塑性区半径参数，时间较长且费用较高[2]；用隧道围岩理论公式法进行塑性区计算时，Morh-Coulomb公式应用较为广泛，可用来计算基于Morh-Coulomb屈服条件的理想弹塑性体[3]，长期的工程实践证明了该公式的合理性，通过理论公式定量确定围岩塑性区半径的方法将对围岩稳定分析有着积极的指导作用[3]。但利用经验公式法求解隧道围岩力学参数涉及参数较多，在应力场复杂的情况下，单纯依赖经典力学理论公式无法给出适合的理论解。为寻求获取隧道塑性区半径的普遍方法，对国内外隧道变形、应力的相关资料进行研究，结果表明，将室内岩石三轴试验得到的岩体力学参数代入Morh-Coulomb给出的强度公式后，经过推导便可以求出我们关心的塑性区半径。国内外有大量对围岩硐室塑性区的研究资料，但是在交叉隧道围岩复杂空间条件下塑性区计算方面的研究却很少。本文为探究交叉隧道硐室周边岩体塑性区相互作用对隧道交叉段围岩稳定性的影响，以草莓沟1#线上跨盘道岭隧道交叉工程为例，对交叉隧道围岩塑性区半径及其相关的影响参数进行分析，并从数值上分析岩体质量好坏与支护强度对围岩塑性区域及稳定性的影响，为交叉隧道施工参数优化提供依据。

1Morh-Coulomb塑性区求解

隧道围岩在长期应力重分布作用下处于稳定状态。当在其上方或下方再次开挖一隧道并产生过大的应力释放，则会造成承载能力降低引发塑性变形。若两隧道近接距离很小，其塑性区将发生重合，形成塑性叠加区域。塑性叠加区域的形状和岩石主应力状态可能发生改变，进而改变围岩的内聚力和内摩擦角等岩石参数，造成岩体抗拉和抗压强度的降低，严重时会使既有或在建隧道近接部位围岩发生破碎松动、剪切破裂滑移等失稳破坏。在进行隧道塑性区计算时，由于隧道硐室长度较大，在隧道轴线方向的应力应变可忽略不计，仅仅考虑隧道纵断面的应力应变，因此可将铁路、公路隧道及矿山巷道等作为平面应力应变问题进行处理[4]。当存在塑性区半径分别为R1和R2的两小净距隧道时，我们可以先假设两隧道的塑性区域能够发生重叠[5-8]，计算各部分的塑性区域，然后通过几何关系求得复杂条件下的塑性范围。在不进行初始地应力测量的情况下，根据国内地下岩土工程相关设计经验，侧压力系数一般取0.8～1.2之间，λ取值为1比较合适，两圆形隧道产生的塑性区叠加场如图1阴影部分所示。

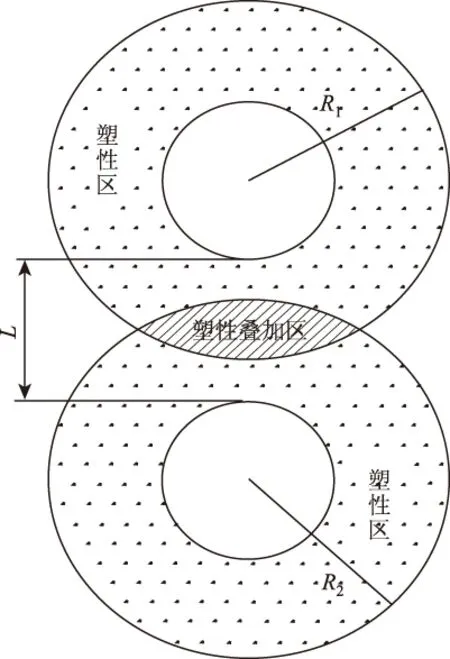
图1　圆形隧道塑性区叠加Fig.1　Superposition of plastic areas in circular tunnel

根据Mohr-Coulomb屈服准则，其屈服平面产生破坏岩体线性方程：

(1)

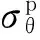
(2)

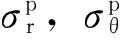
由式(1)和式(2)综合得到：

(3)

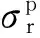
(4)

式中,R0为圆形洞室的半径;Rp为塑性区半径;Pi为作用在隧道临空面围岩的支护力;P0为围岩初始地应力。

由等代圆半径计算方程[9-14]可以计算出较为接近实际的隧道半径：

(5)

式中,B为隧道跨度；α为圆拱对应的圆心角。

为简化计算，计算时令两隧道半径相同，在理想弹塑性岩体中存在R1=R2=Rp,通过式(5)可以得到两隧道半径为5 m。根据《隧道近接交叉施工指南》提出的隧道近接交叉施工影响范围分类以及交叉隧道相互影响范围的划分，见表1。结合草莓沟1#隧道与盘道岭隧道净间距4.24 m小于1.0B(B=10 m)的具体情况，可知两交叉隧道近接距离都在限制范围，属于超小净间距交叉隧道。

表1　交叉隧道相互影响范围的划分

因此，为探讨塑性叠加区域的形状和范围及其影响因素需对相关参数进行分析，塑性区及其影响区域范围为表1中所定的一倍隧道跨度，因而塑性叠加区域范围可认为是两隧道间距与两隧道塑性区范围的差值，即：

(6)

根据塑性区半径方程的表达式，影响围岩塑性区半径的因素主要有：原岩应力P0、支护阻力Pi、内摩擦角φ、黏聚力c、隧道半径R及两隧道结构间距L。下面将其中一个参数作为自变量(自变量的取值可根据参数的取值范围进行变化)，其余作为常量(常量取值可根据所测得的真实数据)，利用绘图软件作出曲线来说明P0,Pi,C,φ,L这几个主要参数对塑性区范围的影响，并结合施工给出最优的围岩支护措施。

1.1黏聚力c对塑性区的影响

令：φ=34°，L=R0=5 m，P0=5.2 MPa。通过产生的图像可以看出，在无支护的情况下内聚力c对塑性区半径的影响近似于平移后的指数方程曲线。随着内聚力的增大塑性区半径减小，在0～3 MPa范围内，下降比较快，而在c大于3 MPa情况下，下降速率减缓，并且随着内聚力不断增大塑性区域趋近于0。这表明完整性越好的围岩所产生的塑性区域的范围越小，围岩越稳定。

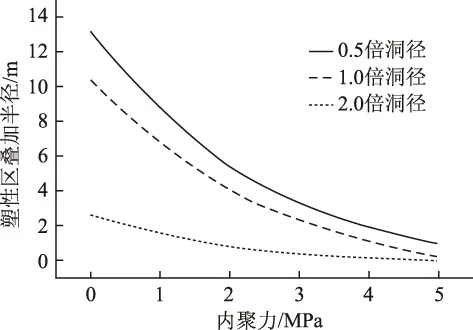
图2　内聚力对塑性叠加区影响曲线Fig.2　Curves of influence of cohesion on plastic overlay area

1.2支护力Pi对塑性叠加区影响

令：φ=34°，c=1.9 MPa，P0=5.2 MPa，代入公式通过绘图软件绘制方程曲线见图3。从图中可以看出，支护力对塑性叠加区域的影响与内聚力相似，当Pi在0～3 MPa范围内时随着支护力的提高，塑性叠加区半径有明显的减小趋势；当Pi大于3 MPa，曲线下降速率变小，说明有支护和无支护下的围岩稳定性差距较大。而随着支护强度增加，其对塑性叠加区加固的效果越来越不显著，并且在近接距离较大的条件下，支护抗力对围岩稳定性提高作用不大。

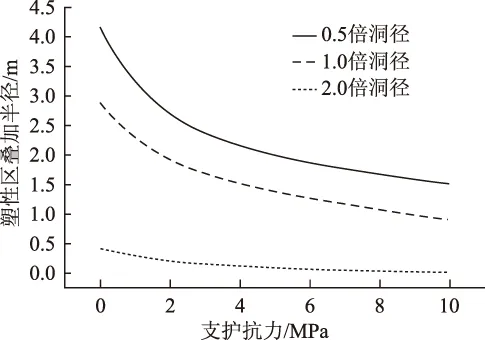
图3　支护抗力对塑性叠加区影响曲线Fig.3　Curves of influence of supporting resistance force on plastic overlay area

1.3内摩擦角对塑性叠加区的影响

令c=1.9 MPa，P0=5.2 MPa，通过绘制方程曲线(图4)可以看出，在无支护的情况下，φ对塑性叠加区半径的影响呈抛物线变化趋势，塑性叠加区半径先减小后增大，呈现出反弯现象；在2倍洞径下，塑性叠加区不存在反弯，并且呈平滑下降趋势,表明颗粒摩擦越大的岩体，其稳定性越好。

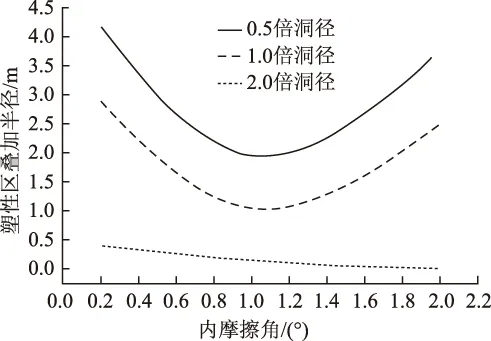
图4　内摩擦角对塑性叠加区影响曲线Fig.4　Curves of influence of internal friction angle on plastic overlay area

1.4原岩应力P0对塑性叠加区的影响

令：φ=34°，c=1.9 MPa，通过绘制方程曲线(图5)可以看出，P0对塑性叠加区半径的影响呈线性变化，并且净间距越小，线性越明显。随着原岩应力增大，塑性叠加区域的范围增大，围岩稳定性降低。

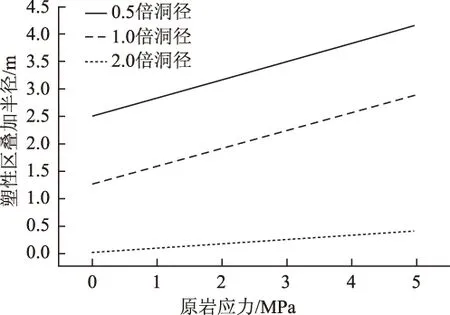
图5　原岩应力对塑性叠加区影响曲线Fig.5　Curves of influence of original rock stress on plastic overlay area

1.5近接距离L对塑性叠加区的影响

令φ=34°，c=1.9 MPa，P0=5.2 MPa，通过绘制方程曲线(图6)可以看出，在无支护的情况下，塑性叠加区随着L的增加呈线性递减趋势，在L大于2倍洞径时，塑性叠加区为0。这表明近接距离越大，近接围岩稳定性越好。

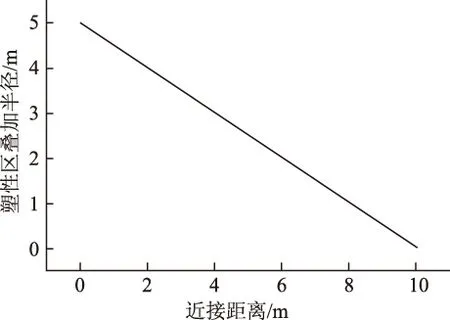
图6　近接距离对塑性叠加区影响曲线Fig.6　Curves of influence of proximity distance on plastic overlay area

2工程实例

新建丹大正线草莓沟1#隧道于DK250+890上跨盘道岭隧道，净距为4.24 m，该交叉段隧道围岩等级为Ⅲ级，岩性主要为混合岩和混合花岗岩成分,弱风化，节理较发育。上部草莓沟1#隧道和下部盘道岭隧道半径各为5 m，交叉段示意图如图7所示。由于交叉隧道埋深为200 m，岩层重度为γ=26 kN/m3，可根据公式P0=γZ求得初始地应力为5.2 MPa。为了得到符合现场实际的岩体力学参数，对交叉段围岩进行取样分析，通过对现场花岗岩试件进行反复加载试验，经计算得到该花岗岩试件的弹性模量E=5.9 GPa，泊松比v=0.25，φ=34°，c=1.9 MPa。所获得的围岩力学参数如表2所示。

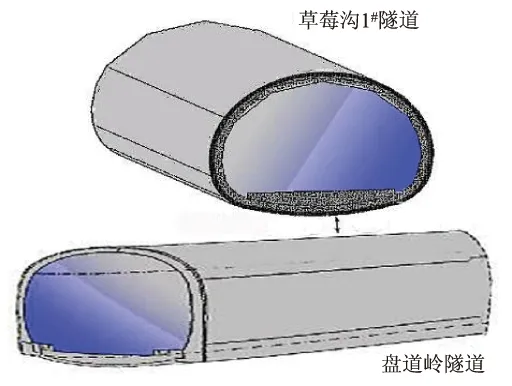
图7　隧道交叉示意图Fig.7　Schematic diagram of tunnel crossing

E/GPavϕ/(°)c/MPaP0/MPaγ/(kN·m-3)5.90.25341.93.926

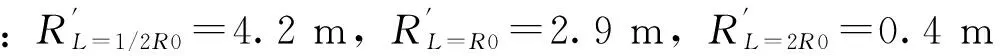
由于两隧道以20°角交叉，因此在立面状态下考虑时本文采用Flac3D有限差分软件对隧道交叉段围岩净空变形进行数值模拟，两隧道交叉部位的竖向剖面可近似为两圆形洞室。在无支护情况下计算交叉断面不同位置围岩塑性叠加区半径模拟结果，如图8所示，其中围岩塑性区剪切应变值在5×10-3以上，数值较大，变形量依次增大；弹性区剪切应变量值在 5× 10-3以下；塑性叠加区位于两隧道近接部位，塑形叠加区呈近似圆形，此部分围岩内部将产生微裂隙，随围岩裂隙持续发展，围岩极有可能产生整体的渐进破坏而造成坍塌失稳。而一般情况下的塑性区产生于隧道临空面上，在力学行为上主要发生围岩向临空面的收敛变化，因此塑形叠加区与一般的塑性区有所差异。如表3所示，当L=0.5R0=2.5 m时，塑性叠加区叠加半径约为4.2 m，其影响范围较大，其相应的剪切应变量范围是10.00～17.50 mm；当L=R0=5 m时，塑性叠加区半径约为2.9 m，其剪切应变量范围是5.00～10.00 mm；当L=2R0=10 m 时，塑性叠加区半径非常小，其相应的剪切应变量范围是2.00～7.00 mm，模拟结果与改进后的Morh-Coulomb准则计算结果吻合。

图8　不同洞径无支护条件下塑性叠加半径Fig.8　Plastic overlay radii of different tunnel diameter without support

3结论

(1)在众多岩体力学参数换算方法中，Morh-Coulomb准则考虑因素比较全面，发展比较完善，可用于山岭立体交叉近接隧道情况下的塑性叠加区半径的计算。

(2) 通过对盘道岭与草莓沟1#线交叉隧道围岩变形进行研究，发现随着两隧道近接距离越小，塑性叠加区范围越大。越靠近塑性叠加区域，围岩变形越大。

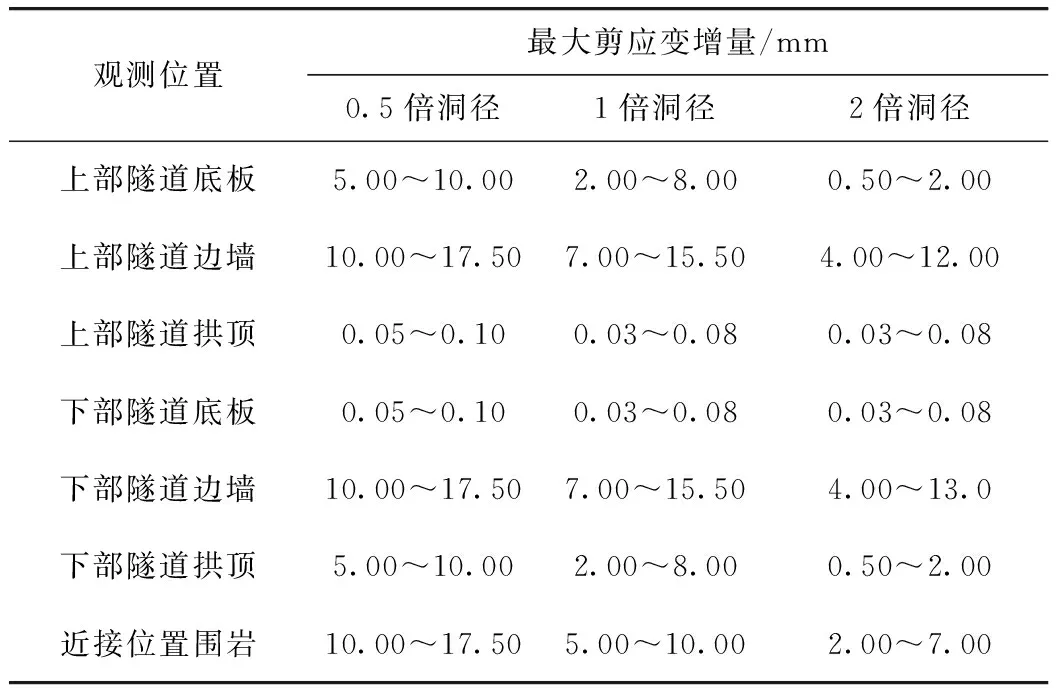
表3　不同位置围岩塑性剪切应变增量

(3)岩石内聚力、支护抗力、岩石内摩擦角、岩石初始应力、近接距离共同决定着交叉隧道围岩塑性叠加半径的大小。

(4)数值模拟结果与改进后的Morh -Coulomb准则计算结果吻合，表明改进后的塑性叠加半径公式能较好地反映交叉隧道围岩稳定程度。

参考文献：

References:

[1]肖同强,李化敏，杨建立，等.超大断面硐室围岩变形破坏机理及控制[J].煤炭学报, 2014, 39(4)：631-636.

XIAO Tong-qiang, LI Hua-min, YANG Jian-li, et al. Deformation and Failure Mechanism of Surrounding Rock in Chamber with Super Large Section and Its Control[J]. Journal of China Coal Society,2014,39(4):631-636.

[2]李胡生，熊文林.岩体力学参数的工程模糊处理[J].水利学报，1994(1)：76-85.

LI Hu-sheng, XIONG Wen-lin. Engineering Fuzzy Treatment of Mechanical Parameters of Rock[J]. Journal of Hydraulic Engineering, 1994(1)：76-85.

[3]曾钱帮,王恩志,王思敬.Hoek-Brown破坏准则求解圆形硐室塑性区半径与修正的芬纳公式比较[J].沈阳建筑大学学报:自然科学版,2008,24(6):933-938.

ZENG Qian-bang，WANG En-zhi，WANG Si-jing. Comparison between Plastic Radius Around a Circular Opening Derived from Hoek-Brown Failure Criterion and Calculated through Modified Fenner Formula [J]. Journal of Shenyang Jianzhu University: Natural Science Edition, 2008, 24(6):933-938.

[4]潘岳，王志强.基于应变非线性软化的圆形硐室围岩弹塑性分析[J].岩石力学与工报, 2005, 24(6): 915-920.

PAN Yue, WANG Zhi-qiang. Elasto-Plastic Analysis on Surrounding Rock of Circular Chamber Based on Strain Nonlinear Softening[J]. Chinese Journal of Rock Mechanics and Engineering, 2005, 24(6): 915-920.

[5]李兆霞，郭力.工程弹性力学[M].南京:东南大学出版社，2009.

LI Zhao-xia, GUO Li. Engineering Elasticity[M]. Nanjing:Southeast University Press, 2009.

[6]刘鸿文.材料力学[M].北京:高等教育出版社，2010.

LIU Hong-wen. Mechanics of Materials[M]. Beijing: Higher Education Press, 2010.

[7]姚延化.基于塑性力学新方法的围岩稳定分析与优化研究[D].长沙:中南大学，2013.

YAO Yan-hua. Stability of Surrounding Rock and Optimization Based on New Method of Plasticity[D]. Changsha: Central South University, 2013.

[8]陈卫忠,郑东,于建新,等. 交叉隧道施工对已有隧道稳定性影响研究[J]. 岩石力学与工程学报,2015(增1):3097-3105.

CHEN Wei-zhong, ZHENG Dong,YU Jian-xin, et al. Study on Stability of Close Cross Tunnel on Existing Tunnel[J]. Chinese Journal o Rock Mechanics and Engineering, 2015(S1):3097-3105.

[9]闫春岭.深埋巷道围岩塑性圈理论分析与研究[J].煤炭科技 ，2012(3):8-10.

YAN Chun-ling. Study and Analysis of Plasticity Ring Theory of Surrounding Rock in Deep Roadway[J]. Coal Science & Technology Magazine, 2012(3):8-10.

[10]李博.隧道建设及运营对建筑物的影响规律研究[D].上海:同济大学,2007.

LI Bo. Study on Effect on Adjacent Structure during Tunnel Construction and Operation[D].Shanghai:Tongji University,2007.

[11]柏建彪，侯朝炯.深部巷道围岩控制原理与应用研究[J].中国矿业大学学报，2006，35(2):145-148.

BAI Jian-biao, HOU Chao-jiong. Control Principle of Surrounding Rocks in Deep Roadway and Its Application[J]. Journal of China University of Mining & Technology, 2006，35(2):145-148．

[12]康红普，王金华，林健.高预应力强力支护系统及其在深部巷道中的应用[J].煤炭学报，2007，32(12):1233-1238．

KANG Hong-pu, WANG Jin-hua, LIN Jian. High Pretensioned Stress and Intensive Bolting System and Its Application in Deep Roadways [J].Journal of China Coal Society, 2007，32(12):1233-1238．

[13]肖同强，柏建彪，王襄禹，等．深部大断面厚顶煤巷道围岩稳定原理及控制[J].岩土力学，2011，32(6):1874-1880．

XIAO Tong-qiang, BAI Jian-biao, WANG Xiang-yu,et al. Stability Principle and Control of Surrounding Rock in Deep Coal Roadway with Large Section and Thick Top-coal[J]. Rock and Soil Mechanics,2011，32(6): 1874-1880．

[14]张占涛.大断面煤层巷道围岩变形特征与支护参数研究[D].北京:煤炭科学研究总院,2009.

ZHANG Zhan-tao. Study on Deformation Features of Surrounding Rock of Large Sectional Roadway in Coalmines and Supporting Parameters[D]. Beijing: Coal Science Research Institute, 2009.

Analysis on Surrounding Rock Plastic Overlay Area of Adjacent and Crossing Tunnel Based on Morh-Coulomb Strength Criterion

JIA Bao-xin1,2, JIANG Ming1, ZHAO Pei1, JIA Zhi-bo1

(1.School of Civil Engineering and Transportation, Liaoning Technical University, Fuxin Liaoning 123000, China;2. Geological Research Institute, China Earthquake Administration, Beijing 100000, China)

Abstract：To identify the radius of plastic superposition area of adjacent chamber of cross tunnel and analyze its influence on the stability of surrounding rock of cross tunnel, based on the Morh-Coulomb strength criterion which is most widely used in engineering mechanics, through theoretical derivation, the plastic overlay area scope and corresponding analytical solution under the influence of small clear distance is obtained. On this basis, the influencing factors of the stability of proximity surrounding rock are discussed. The result shows that the superposition radius of the cross tunnel plastic zone is related to the cohesive force, the supporting force, the internal friction angle, the original rock stress, the near distance, etc. Comparing the data calculated by Morh-Coulomb strength equation with real measurement data, they are consistent, which shows that the presented plastic area calculation formula can better reflect the stability of the surrounding rock of the cross tunnel.

Key words：tunnel engineering; surrounding rock stability; Morh-Coulomb criterion; cross tunnel; small clear distance; plastic overlay area

收稿日期：2014-12-18

基金项目：国家重点基础研究发展计划(九七三计划)项目(2010CB226803)；辽宁省自然科学基金项目(201204414)；辽宁省教育厅自然科学项目(L2012107)

作者简介：贾宝新(1978-),男,辽宁抚顺人，副教授.(jbx_811010@126.com)

doi:10.3969/j.issn.1002-0268.2016.05.015

中图分类号：U451+.2

文献标识码：A

文章编号：1002-0268(2016)05-0092-06