基于权函数法的沥青混合料预切口小梁的断裂理论与裂纹扩展试验的研究

李　萍，马　科，念腾飞，吴　中，郭云枫

(1. 兰州理工大学　土木工程学院，甘肃　兰州　730050;2. 甘肃第七建设集团股份有限公司　基础桥梁市政工程公司，甘肃　兰州　730000)



基于权函数法的沥青混合料预切口小梁的断裂理论与裂纹扩展试验的研究

李萍1，马科1，念腾飞1，吴中1，郭云枫2

(1. 兰州理工大学土木工程学院，甘肃兰州730050;2. 甘肃第七建设集团股份有限公司基础桥梁市政工程公司，甘肃兰州730000)

摘要：为研究沥青面层底部裂缝的应力状态和扩展规律，基于权函数法对含单边裂纹的矩形板权函数进行了理论推导，基于切口小梁的试验模型和单边预切口小梁的三点弯曲试验，研究Ⅰ-Ⅱ型应力强度因子、Ⅰ-Ⅱ复合型断裂判据和裂纹在沥青混合料中的扩展变化规律。结果表明：相同的荷载作用下，切口越靠近加载点，Ⅰ型应力强度因子和最大能量释放率越大，Ⅱ型应力强度因子和开裂角越小；切口越长，最大能量释放率越大，小梁越容易开裂；在切口不对称的情况下对小梁加载出现了Ⅰ-Ⅱ复合型开裂，且起裂荷载随着切口偏离加载点距离的增大而增大。通过理论计算与数值模拟结果的对比，使用权函数法计算小梁Ⅰ-Ⅱ复合型裂纹应力强度因子具有良好的精度。

关键词：道路工程；沥青混合料；权函数法；裂纹扩展：预切口小梁；应力强度因子

0引言

裂缝是沥青路面突出的病害之一。目前研究裂缝问题的方法主要有断裂力学理论、试验以及数值模拟[1-2]，根据裂缝在路面中受力性状的不同主要可以分为Ⅰ型和Ⅰ-Ⅱ复合型。Majidzadeh[3]最先将断裂力学引入到路面研究中，通过运用断裂力学对路面裂缝的模拟，Majidzadeh将沥青路面的疲劳破坏分为3个阶段：裂缝初始化阶段、裂缝扩展阶段和极限断裂阶段。黄晓明等人[4]以裂纹面所受的均匀拉应力为参考荷载，运用单个参考荷载的权函数模型来计算沥青面层底裂纹的应力强度因子。Wagoner等人[5]通过SEB试验结合数值模拟对沥青混凝土的断裂能和反射裂缝的扩展机理进行了研究，研究表明SEB试验是研究裂缝扩展机理较为有效的方法。基于光弹性法模型试验，张起森等人[6]研究了开裂后的沥青路面结构在交通荷载作用下裂缝附近的应力状态及裂缝稳定性扩展问题。目前为止，关于沥青路面裂缝的研究主要是围绕着Ⅰ型裂纹来开展的，对Ⅰ-Ⅱ复合型裂纹扩展的研究尚不多[7-9]。

研究沥青路面裂缝在不同扩展深度和扩展方向的受力状态及扩展规律，对于预测路面开裂以及进行路面结构优化设计具有重要的意义。本文基于断裂力学和权函数理论，推导并计算了小梁构件裂纹尖端的应力强度因子和能量释放率，并采用带偏置切口的小梁弯曲试验来研究沥青混合料的开裂与裂纹扩展规律。

1权函数法与Ⅰ-Ⅱ复合型断裂判据

1.1权函数法基本思想

断裂力学理论要解决的关键问题之一是求解表征裂纹端部应力奇异性强弱的应力强度因子。对于复杂应力条件下的应力强度因子，Bueckner[10]提出了应力强度因子的权函数法,即任意荷载作用下的裂纹体，其裂纹尖端的应力强度因子可通过式(1)得到：

(1)

式中，a为裂纹长度；σ(x)为裂纹面位置对应的无裂纹时的应力分量；m(x,a)为权函数。

权函数只与裂纹体的几何形式有关，不同裂纹体的权函数有不同的表示方法，Glinka和Shen[11]提出了一种应用较为广泛的权函数表达式：

(2)

式中Mi(i=1,2,3)是几何参数，其值仅取决于裂纹体的几何形式。

如果已知3个特殊的参考应力分量σri(i=1,2,3)下的参考应力强度因子Kri(i=1,2,3)， 把σri，Kri和式(2)代入到式(1)，就可以建立关于Mi的3个方程，从而可以计算出Mi。

1.2带单边裂纹的矩形板的权函数

为了对比切口小梁试验研究，本文选取了带边缘裂纹的矩形板来进行理论计算。Fett[2]证明了在边缘裂纹体的裂纹末端(x=0)，裂纹面的曲率为0，进而推导出：

(3)

式(3)可以作为求解Mi的附加条件，这样就只需要寻求两个参考应力强度因子解。对于Ⅰ型裂纹，选取图1所示的两种参考荷载。

(4)

式中W为小梁试件的高度。

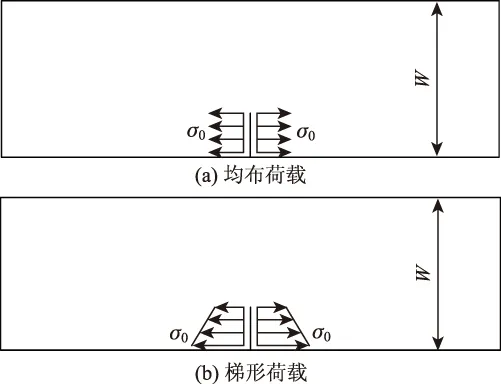
图1　参考荷载Fig.1　Reference load

对应的参考应力强度因子解分别为：

(5)

式中Fi(i=1,2)为参考应力强度因子的几何修正系数，通过应力强度因子手册[12]查得：

(6)

将式(2)、(4)、(5)代入式(1)，式(2)代入式(3)，就可以得到关于Mi(i=1,2,3)的3个方程：

(7)

进而推导出：

(8)

最后，将式(8)代入式(2)就得到Ⅰ型裂纹的权函数表达式。

同样，Ⅱ型裂纹也可以运用上述方式来计算其权函数，但寻找特殊参考荷载作用下的应力强度因子的解析解比较困难。本文运用了Fett[14]推荐的Ⅱ型裂纹另一种形式的权函数mⅡ(x,a)：

(9)

式中，权函数系数Aνμ通过边界配置法计算得到，具体详见文献[13]。

1.3计算算例

本文以切口小梁的试验模型为例来进行应力强度因子的计算，见图2。小梁试件长250 mm，高W和宽B均为50 mm,跨径S为200 mm；切口长度a分别为10，15，20，25 mm和30 mm。切口与荷载作用线的距离L分别为0，10，20，30 mm和40 mm。梁跨中间作用集中荷载P=500 N。

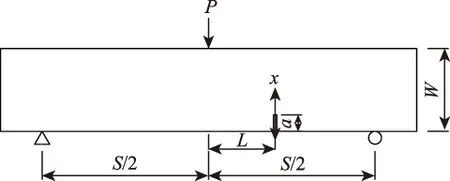
图2　单边切口小梁Fig.2　Single-edge notched beam

在没有切口的情况下，梁上任一点的应力为：

(10)

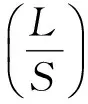
所得数据均以均数±标准差表示，采用SPSS 24.0软件进行统计学分析，组间比较采用单因素方差分析，两两比较采用LSD-t法，P＜0.05为差异有统计学意义。

(11)

通过预制不同位置的切口，可以模拟不同状态的Ⅰ-Ⅱ复合型裂纹。对应的应力强度因子可分为Ⅰ型和Ⅱ型两种，分别用KⅠ和KⅡ表示。将式(10)结合对应的权函数代入到式(1)，则有：

(12)

(13)

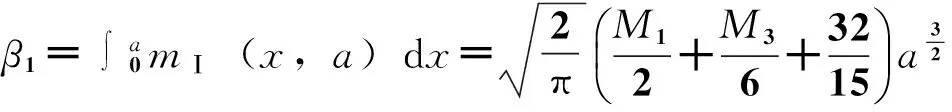
经过计算，得到了不同切口长和不同切口位置的应力强度因子。为了方便比较，以切口长与梁高比ρ=a/W以及切口相对位置γ=2L/S作为变量来进行分析。Ⅰ型和Ⅱ型应力强度因子随ρ的变化关系见图3和图4。可以看出，两种应力强度因子都随着切口长度的增大而增大。其中，KⅠ呈现出非线性增长的变化规律，增长速率逐渐增大；KⅡ则在切口偏置位移非零时接近线性增长。当ρ从0.2变化到0.4(即切口长度从10 mm增长到20 mm)，KⅠ增长了68.7%，KⅡ则增长了138.9%，这说明切口长度对切口尖端的应力场有显著的影响。同一切口的KⅠ均显著大于KⅡ，表明张开型断裂模式在复合型裂纹扩展中起着关键的作用。KⅠ和KⅡ随γ的变化关系如图5和图6所示。可以看出，在相同切口长度的条件下，KⅠ随着切口偏离加载点距离的增大而减小，且与γ呈线性变化关系；KⅡ则随γ呈现出非线性增长的规律，且增长速率逐渐减小直至趋近为0，表明切口偏离荷载位置越远，滑移型断裂模式表现得越明显。当γ≥0.3(L≥30 mm)时，切口与荷载距离的增长对KⅡ的影响趋于稳定。

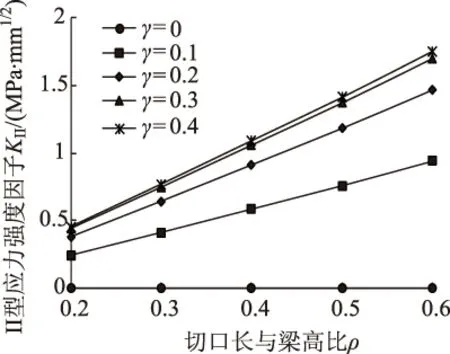
图4　KⅡ随ρ的变化关系Fig.4　KⅡ vs. ρ

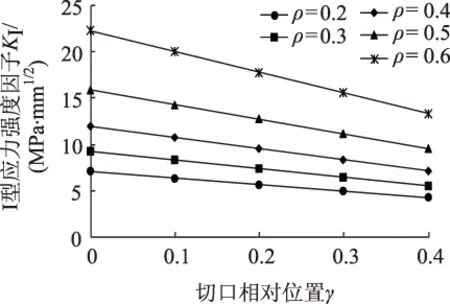
图5　KⅠ随γ的变化关系Fig.5　KⅠ vs. γ

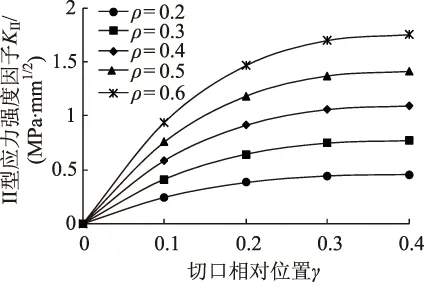
图6　KⅡ随γ的变化关系Fig.6　KⅡ vs. γ

1.4Ⅰ-Ⅱ复合型断裂判据

复合型裂纹扩展要解决两个基本问题：开裂角和断裂判据，即研究裂纹什么条件下沿什么方向开始扩展。本文运用最大能量释放率准则来研究Ⅰ-Ⅱ复合型断裂判据。Hussain等人[15]提出了Ⅰ-Ⅱ复合型裂纹沿θ方向的能量释放率G(θ)表达式：

(14)

根据最大能量释放率准则，裂纹沿G(θ)取最大值方向扩展，故开裂角θ0满足：

(15)

(16)

记λ=KⅡ/KⅠ，开裂角θ0由式(15)确定，即：

(17)

把θ0和式(14)代入到式(16)可得Ⅰ-Ⅱ复合型断裂判据：

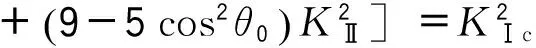
(18)

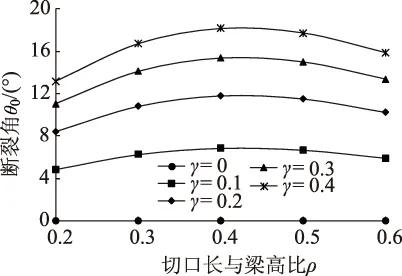
图7　θ0随ρ的变化关系Fig.7　θ0 vs. ρ

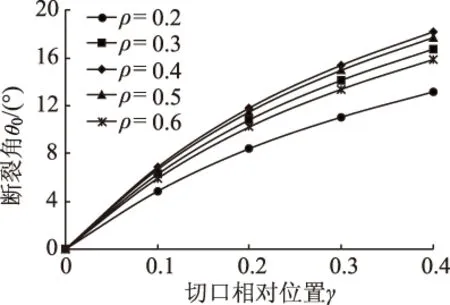
图8　θ0随γ的变化关系Fig.8　θ0 vs. γ

仍以图2所示的预切口小梁为例，假设小梁的弹性模量为E=1 500 MPa，其他条件不变。式中应力强度因子由上文权函数计算得到。在平面应力情况下，应用上述公式计算的开裂角θ0和对应的最大能量释放率G(θ0)见图7～图10。可以看到，当γ=0(切口位于集中荷载正下方)时，开裂角θ0=0，表明当切口位于梁跨正中间并对称加载时，小梁会沿原裂纹方向开裂，表现为纯Ⅰ型开裂模式。切口偏离荷载位置时，θ0随着ρ的增大呈现先增大后减小的趋势。当ρ增大到0.4时，θ0最大，说明此时Ⅰ-Ⅱ复合型裂纹扩展模式在小梁中表现得最为明显。最大能量释放率G(θ0)随着ρ的增大而增大，增长速率也逐渐增加。可见，切口越长，就越容易使G(θ0)达到材料的断裂韧性GⅠc，小梁就越容易开裂。当切口长度一定时，θ0随切口相对位置γ的增大而增大，增长速率逐渐减小，G(θ0)则随着γ增大而逐渐减小。这表明同样的荷载作用下，γ越大越不容易开裂；换言之，切口偏离荷载位置越远，要使小梁开裂的荷载越大。

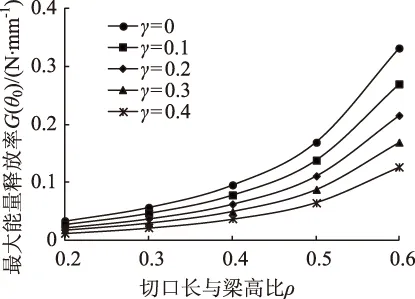
图随ρ的变化关系Fig.s. ρ

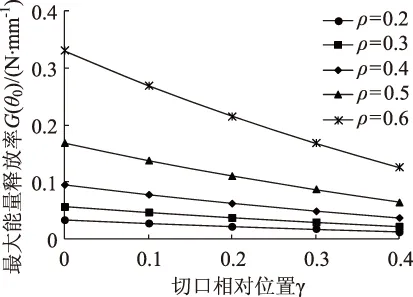
图随γ的变化关系Fig.s. γ

1.5数值模拟对比

为了验证上文理论计算的准确性，本文采用ABAQUS内置的扩展有限元(XFEM)对预切口小梁进行了模拟计算，并将数值模拟计算的结果与理论计算的结果进行对比分析。采用结构化网格技术将模型划分成25 200个C3D8R六面体单元，共计28 224 个节点，对预制切口左右各30 mm范围内的网格进行加密,如图11所示。

图11　切口小梁模型的网格划分Fig.11　Mesh for notched beam model

取ρ=0.2(即a=10 mm)时不同切口位置的计算结果进行对比(其他条件同理论计算的条件一致)。应力强度因子和最大能量释放率的对比结果见表1。可以看出切口偏离荷载的情况下，理论计算的KⅠ和G(θ0)相比数值模拟的结果偏小，KⅡ则偏大，但总体上比较接近。这说明本文推导的权函数在计算小梁断裂问题上具有一定的可靠度。

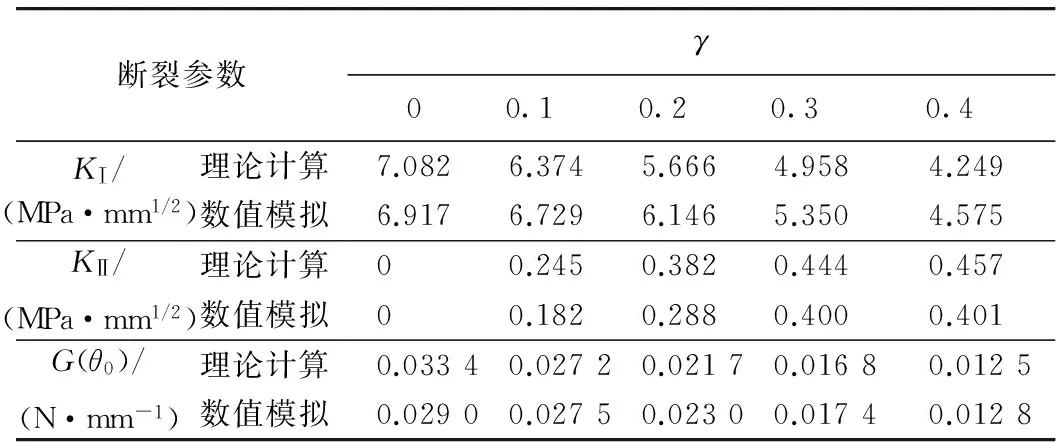
表1　理论计算结果与数值模拟结果的对比

2单边预切口梁的试验研究

2.1试验概况

本文采用AC-13的沥青混凝土切口小梁进行三点弯曲试验。小梁试件是通过尺寸为300 mm×300 mm×50 mm的标准板试件切割而成，具体操作采用了《公路工程沥青及沥青混合料试验规程》(JTG—E20—2011)中的方法。小梁的切口通过金刚石锯片切割机制作，由于锯片自身厚度的影响和其他试验条件的限制，预制的裂纹并非尖锐的“V”形，而是呈相对粗糙的“U”形，如图12所示。成型的切口小梁试件的尺寸以及切口位置同理论计算的模型一致，见图2，切口深度则采用了10，20，30 mm这3种。

图12　切口小梁试件Fig.12　Single-edge notched beam specimens

试验加载设备为长沙亚星沥青混合料弯拉试验系统，全部试验过程在20 ℃温度下进行，加载速率为50 mm/min。试验操作具体方法见《公路工程沥青及沥青混合料试验规程》(JTG—E20—2011)中沥青混合料弯曲试验(T 0715—2011)。

2.2试验结果分析

试验获得了不同切口位置和不同切口长度的小梁在裂纹出现时的最大荷载PB(也称“起裂荷载”)。PB随切口相对位置γ的变化关系如图13所示。可以看出，在相同切口长度条件下，切口距离荷载作用位置越远，起裂荷载PB越大，这与权函数法推导的结论一致。另外，从图上也可以看出同一位置的切口，ρ越大(即切口越长)，PB越小，表明小梁越容易产生裂纹。当ρ=0.6(即a=30 mm)时，沥青混合料小梁在很小的外部荷载作用下就会发生断裂。

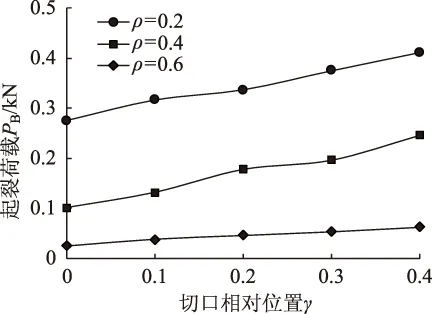
图13　PB随γ的变化关系Fig.13　PB vs. γ

对裂纹扩展的观察发现，裂纹会先经历一段稳定的发展过程，当裂纹扩展到一定程度时便会迅速贯穿小梁而发生断裂。如图14所示，切口尖端的裂纹是朝着荷载作用位置的方向开裂的，且切口偏移量越大，开裂角越大，表现为Ⅰ-Ⅱ复合型裂纹的扩展行为。同时可以看到，裂纹扩展路径存在不同程度的转折，这主要是由于沥青混合料并非均质材料，集料颗粒的存在影响了裂纹在沥青混合料中的扩展形式。裂纹扩展到一定长度后，应力重分布使小梁切口的受力状态逐渐接近Ⅰ型裂纹的受力状态，因而出现了裂纹向竖直方向转折的现象。

图14　切口小梁的裂纹扩展Fig.14　Crack propagation of notched beam

3结论

本文通过断裂力学理论和三点弯曲试验对小梁切口尖端的应力强度因子和裂纹扩展规律进行了研究。研究结果有助于认识沥青混合料的裂纹产生和扩展机理，对后期相应计算程序的编制以及沥青路面开裂的预测有着一定理论和工程价值。本文主要结论如下：

(1)相同荷载作用下，切口越长，其尖端的应力强度因子和最大能量释放率越大，小梁越容易开裂；当切口长与梁高比达到0.4时，Ⅰ-Ⅱ复合型裂纹扩展模式表现得最为明显。

(2)相同荷载作用下，切口偏离加载点越远，Ⅰ型应力强度因子和最大能量释放率越小，开裂角和Ⅱ型应力强度因子越大；Ⅰ型断裂模式在复合型裂纹扩展中起着关键作用。

(3)当切口偏离加载位置时，小梁表现出Ⅰ-Ⅱ复合型开裂；起裂荷载随着切口偏离距离的增大而增大；裂纹向上扩展过程中逐渐接近Ⅰ型裂纹形式。

(4)本文推导的权函数在计算切口小梁的应力强度因子上具有良好的精度。

参考文献：

References:

[1]赵延庆, 王抒红, 周长红, 等. 沥青路面Top-Down裂缝的断裂力学分析[J]. 同济大学学报:自然科学版, 2010, 38(2): 218-222.

ZHAO Yan-qing, WANG Shu-hong, ZHOU Chang-hong, et al. Analysis of Top-Down Cracking of Asphalt Pavements Based on Fracture Mechanics Approach[J]. Journal of Tongji University:Natural Science Edition, 2010, 38(2): 218-222.

[2]车法, 陈拴发, 李增宏, 等. 荷载作用下沥青路面表面开裂的扩展[J]. 公路交通科技, 2010, 27(5): 26-29,51.CHE Fa, CHEN Shuan-fa, LI Zeng-hong, et al. Analysis of Cracks Propagation on Asphalt Pavement Surface under Load [J]. Journal of Highway and Transportation Research and Development, 2010, 27(5): 26-29,51.

[3]MAJIDZADEH K, BURANAROM C, KARAKOUZIAN M. Application of Fracture Mechanics for Improved Design of Bituminous Concrete, Final Report[R]. Washington, D.C.: Federal Highway Administration, 1976: 76-91.

[4]罗睿,黄晓明. 利用权函数计算沥青路面层间部分约束的面层底裂缝应力强度因子[J]. 岩土工程学报, 2001, 23(5): 610-613.

LUO Rui, HUANG Xiao-ming. Calculation on the Stress Intensity Factor for the Bottom Crack of Asphalt Layer in Asphalt Pavement Considering Partial Constraint by Weight Function[J]. Chinese Journal of Geotechnical Engineering, 2001, 23(5): 610-613.

[5]LINK R E, WAGONER M P, BUTTLAR W G, et al. Development of a Single-edge Notched Beam Test for Asphalt Concrete Mixtures[J]. Journal of Testing and Evaluation, 2005, 33(6): 452.

[6]张起森, 刘益河. 沥青路面开裂机理分析及试验研究

[J]. 长沙交通学院学报, 1988,4(2):67-80.

ZHANG Qi-sen，LIU Yi-he. Analysis and Testing Investigation on Cracking Mechanism of Asphalt Pavements[J]. Transactions of Changsha Communications College , 1988,4(2):67-80.

[7]毛成, 邱延峻. 沥青混凝土复合型裂纹扩展行为数值模拟[J]. 公路交通科技, 2006,23(10): 20-24.

MAO Cheng，QIU Yan-jun. Numerical Simulation of Compound Crack Propagation Behavior of Asphalt Concrete[J]. Journal of Highway and Transportation Research and Development, 2006, 23(10): 20-24.

[8]罗辉, 朱宏平, 陈传尧. 预切口沥青混合料小梁疲劳试验与数值研究[J]. 土木工程学报, 2009,42(6): 126-132.

LUO Hui, ZHU Hong-ping, CHEN Chuan-yao. The Fatigue Test and Numerical Study on Pre-sawed Bituminous Mixture Beams[J]. China Civil Engineering Journal, 2009,42(6): 126-132.

[9]罗辉, 朱宏平, 陈传尧. 有限元-无网格伽辽金耦合方法模拟沥青路面裂纹扩展[J]. 公路交通科技, 2008, 25(9): 1-6.

LUO Hui, ZHU Hong-ping, CHEN Chuan-yao. Modelling of Crack Propagation in Asphalt Pavements by the Coupled EFG and FE Method[J]. Journal of Highway and Transportation Research and Development, 2008, 25(9):1-6.

[10]BUECKNER H F. A Novel Principle for the Computation of Stress Intensity Factors[J]. Zeitschrift Fuer Angewandte Mathematik & Mechanik,1970, 50(9):529-546.

[11]SHEN G, GLINKA G. Weight Function for a Surface Semi-elliptical Crack in a Finite Thickness Plate[J]. Theoretical and Applied Fracture Mechanics, 1991, 15(3): 247-255．

[12]仇仲翼. 应力强度因子手册[M]. 北京: 科学出版社, 1993.

QIU Zhong-yi. Handbook of Stress Intensity Factors[M]. Beijing: Science Press, 1993.

[13]FETT T, MATTHECK C, MUNZ D. On the Calculation of Crack Opening Displacement from the Stress Intensity Factor[J]. Engineering Fracture Mechanics, 1987, 27(6): 697-715.

[14]FETT T. Mixed-mode Stress Intensity Factors for Three-point Bending Bars[J]. International Journal of Fracture, 1991, 48(4): 67-74.

[15]HUSSAIN M A, PU S L, UNDERWOOD J. Strain Energy Release Rate for a Crack Under Combined Mode I and Mode II[C]//Proceedings of the 1973 National Symposium on Fracture Mechanics, Fracture Analysis. Md.:ASTM Publications, 1973:2-28.

Study on Fracture Theory and Crack Propagation Test of Asphalt Mixture Pre-notched Beam Based on Weight Function Method

LI Ping1, MA Ke1, NIAN Teng-fei1, WU Zhong1, GUO Yun-feng2

(1. School of Civil Engineering, Lanzhou University of Technology, Lanzhou Gansu 730050, China;2. Foundation, Bridge &Municipal Engineering Corporation, Gansu Provincial 7th Construction Group Co., Ltd.,Lanzhou Gansu 730000, China)

Abstract：In order to research the stress state and the crack propagation of asphalt surface course bottom， the weight function of rectangular plate with single edge crack is derived based on weight function method, the I-II mixed mode stress intensity factor, mixed mode fracture criterion and propagation law of crack in asphalt mixture are studied based on the test model of pre-notched beam and three-point bending test of single-edge notched beam. The result shows that (1) under the same load, with the notch closes to the loading point, stress-intensity factor and the maximum energy release rate of mode I increase while the stress-intensity factor and the fracture angle of mode II decrease; (2) the longer the notch, the greater the maximum energy release rate and the easier the beam to be cracked; (3) the mixed-mode cracking appears in the case of asymmetric notch, and the initial cracking load increases with the increase of notch offset distance. Comparing the theoretical and simulation results, it has a good precision to calculate the crack stress intensity factor of the beam by weight function method.

Key words：road engineering; asphalt mixture; weight function method; crack propagation; pre-notched beam; stress intensity factor

收稿日期：2015-01-20

基金项目：国家自然科学基金项目(51108222)；甘肃省科技支撑项目(1504GKCA031)

作者简介：李萍(1972-)，女，江苏靖江人，博士，教授.(liping@lut.cn)

doi:10.3969/j.issn.1002-0268.2016.05.004

中图分类号：U416.217

文献标识码：A

文章编号：1002-0268(2016)05-0021-07