农村供应链金融复杂网络演化模型研究
2016-06-12陈琼琼翟帅男浙江理工大学
陈琼琼 翟帅男 浙江理工大学
农村供应链金融复杂网络演化模型研究
陈琼琼 翟帅男 浙江理工大学
摘 要:农村电子商务的快速发展催生农村地区的资金需求日益增加,供应链金融为满足农村资金需求提供了新的融资模式,成为支持农村电子商务发展的重要保障。
关键词:供应链金融 复杂网络 无标度 小世界效应
一、引言
农户受信贷约束的问题在我国农村普遍存在。在农村地区开展供应链金融模式,能够适应农业产业化发展过程中出现“公司+农户”的组织架构,解决金融机构开展农村金融业务面临的诸多掣肘,具有应用于“三农”发展的必要性和可行性[1]。现有的供应链金融研究集中于研究特定的融资模式,从宏观层面的研究很少。用复杂网络理论通过网络结构演化的行为方式描述整个系统的演化机制和整体行为。国外对复杂网络描述社会网络已取得一定的研究成果,复杂网络的基本模型主要有:随机网络,聚集系数小,节点之间的关系并不紧密[2]。小世界模型用来描述现中庞大且复杂的网络,聚集系数较高,节点之间联系紧密[3]。无标度网络的顶点与边的生长连接方式具有一定的规则,引入了择优机制,该模型具有较高的无标度特性[4],沈爱忠从复杂网络视角对供应链金融网络拓扑进行分析,认为供应链金融网络具有无标度特性[5]。
二、农村供应链金融复杂网络模型
农村供应链金融网络包括金融机构、电商平台、P2P平台、物流企业和农户五层节点,每个层次内的节点同质。供应链金融网络组织结构演化过程:受融资需求影响不断调整,不适应的节点消失,与网络相适应的节点加入,融资渠道的创新又会形成一系列新的金融供应链。
本文以无标度网络模型为参考模型,以节点存在择优性为依据,为更贴切实际网络的连接特征,通过引入多个随机量(如边的权值)增加供应链金融网络的真实性,提出分层的加权供应链金融网络演化模型。
本文提出的分层供应链网络演化模型基本演化规则为:
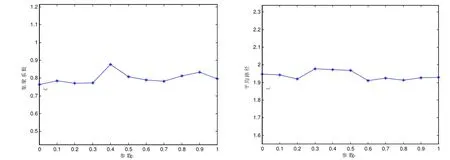
供应链金融网络G在t=0时刻是由n0个节点构成的层次型网络,共有5层节点:金融机构、电商、P2P、物流企业、农户。假设边的权值随机生成,初始wi设定为2。在以后的每一个时间步里,新增一个度为mi的节点(mi (1)增长。产生随机整数A∈(0,5],根据A值区别不同层次的新增节点,跨层连接规则如下:A=1时,表示新增节点为第一层的金融机构节点,它可以与第二层、第三层、第五层的节点相连。A=2,表示新增节点为第二层的电商平台节点,它可以与第五层的节点相连。A=3,表示新增节点为第三层的P2P平台节点,它可以与第五层的节点相连。A=4,表示新增节点为第四层的物流企业节点,它可以与第一层和第五层的节点相连。A=5时,第五层节点可与任意四层节点相连。 (2)择优选择。新增t个时间步后,新增节点选择与网络中已存在的mi个不同的老节点相连。被选择的节点vi与新节点连接的概率为: 其中si,为节点vi的强度,ki为节点vi的度数,为受偏好影响节点重要度的参数。 (3)边权演化。初始对边值w0都赋予权值,参照有向加权模型的边权演化规则,本文认为新加入的边会使连接节点vi和节点vj之间的边发生相应的变化: 此外,金融市场收益的“尖峰厚尾”特征,尖峰峰度大于3(正态分布的峰度),直观上来讲比正态分布更为陡峭。出于网络节点企业的交易量增加真实性目的,在节点的边权演化中引入贝塔分布的概率密度函数B。 本文采用的仿真软件为matlab7.12.0,根据上述算法生成节点数N=100的供应链金融网络模型,对供应链金融初始网络节点N=1000开始演化,通过选取不同的值选择网络的数值模拟。根据试验中拟合p(k)~k-γ的结果得出网络中,度大的节点出现的概率较少,大量度值是出现在低概率中。 此外,不同偏好因子(p值)下的集聚系数变化较小,整体的集聚系数的值较大。随着网络规模的增长,网络的平均路径长度也有一定的增长,但整体来说变化较小。网络模型的集聚系数和平均路径长度的变化特征体现了供应链金融网络具有小世界特性。事实上,较小的平均路径长度体现了跨层点对整个网络的信息传递起到非常重要的作用。 总结,仿真结果中度分布存在“长尾效应”,属于幂率分布,点强度分布和度分布成正相关,平均最短路径随着偏好参数的变化并没有大幅度调整,而网络的集聚系数很大。因此,供应链金融网络具有无标度特征和小世界效应。 参考文献: [1]谢斯儒. 供应链金融应用于“三农”发展的必要性与可行性[J]. 经济视角(下),2011,09:99-101. [2]A.Erd s, P.;Rényi, A. On the evolution of random graphs. Bull. Inst. Internat. Statist,1961,38:343-347. [3] Watts, Duncan J, Strogatz, Steven H. Collective dynamics of small-world networks. NATURE, 1998,393( 6684): 440-442. [4] Wat Barabasi AL;Albert R. Emergence of scaling in random networks. Science (New York, N.Y.), 1999,286( 5439): 509-512. [5]沈爱忠,郭进利. 复杂网络理论视角下供应链金融风险分析与控制[J]. 科技与管理,2013,05:107-110.

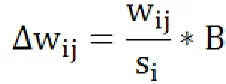
三、实验分析