整环上的w－凝聚性

尹华玉， 陈幼华

整环上的w－凝聚性

尹华玉， 陈幼华

(四川师范大学数学与软件科学学院，四川成都610066)

利用w－算子理论，结合无挠模对整环上的相关w－凝聚性进行细致的讨论，证明整环R是WFC整环当且仅当R的任意2个主理想的交是有限型的，当且仅当R的每个2－生成理想是有限表现型的，当且仅当每个2－生成无挠R－模是有限表现型的．此外，引入拟凝聚整环的w－拓展，并给出其相应的等价刻划．

w－算子;凝聚整环;WFC整环;w－拟凝聚整环

1 预备知识

众所周知，经典的Noether环理论是交换代数的重要内容，而凝聚环是其中一个很好的推广．随着20世纪80年代星型算子工具的引进，整环上的凝聚性也引起了许多环论学者的关注，例如拟凝聚整环、FC整环、w－凝聚整环、WFC整环等．本文恒设R是具有单位元的交换整环但不是域，K是R的商域，所涉及的模类均为R－模．设A是K的R－子模，若存在非零元素a∈R，使得aA R，这等价于说存在非零元素c∈K，及R的非零理想I，使得A= cI，则称A为R的分式理想．用F(R)表示R的所有非零分式理想的集合，所谓整环R上的星型算子，指的是从F(R)到自身上的一个映射*:A→A*，对 A，B∈F(R)，a∈K－0，满足以下条件:

1)(a)*=(a)，(aA)*=aA*;

2)若A B，则A*B*;

3)A A*，且(A*)*=A*．

设A是K的R－子模，令A－1={x∈K|xA R}，定义

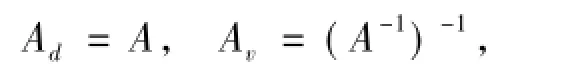
At=∪{Bv|B取遍A的一切有限生成子分式理想}，以上d－、v－与t－算子即是较常见的三类星型算子，但它们只能刻划K中的R－子模，其研究具有较大的局限性．F．G．Wang等［1］引入了一个新的星型算子，即w－算子，它可以对整环上的无挠模类进行研究与刻划．设M是无挠R－模，定义

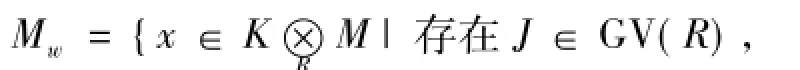
使得Jx M}，其中，GV(R)={J|J是R的有限生成理想，且J－1=R}，称之为M的w－包络．若Mw=M，则称M为w－模．若M是R的理想，且Mw=M，则称M为R的w－理想．易知w:F(R)→F(R)也是一个星型算子，称之为w－算子．关于星型算子的知识与w－模理论及文中的相关概念与符号可参见文献［1－9］．

基于w－算子在模类上的拓展，本文将利用w－算子理论，结合无挠模对整环上的相关w－凝聚性进行细致的讨论．

2 凝聚整环、FC整环与拟凝聚整环

设R是整环，若R的每个有限生成理想是有限表现的，则称R为凝聚整环．若对任意x∈K－0，(R:x)={r∈R|rx∈R}都是R的有限生成理想，则称R为FC整环．若对R的每个非零有限生成理想I，I－1是有限生成分式理想，则称 R为拟凝聚整环［2］．为了直观地区分此3类整环的凝聚性，给出它们的一些等价刻划．

定理2．1 对整环R，以下各条件等价:

1)R是凝聚整环;

2)R的任意2个有限生成理想的交是有限生成的;

3)R的任意n(n∈Z+)个有限生成理想的交是有限生成的;

4)每个有限生成无挠模是有限表现的．

证明 1) 2) 4)参见文献［2］，而2) 3)是平凡的．

定理2．2［2］对整环R，以下各条件等价:

1)R是FC整环;

2)R的任意2个主理想的交是有限生成的;

3)R的每个2－生成理想是有限表现的;

4)每个2－生成无挠模是有限表现的．定理2．3 整环R是拟凝聚的当且仅当R的任意n(n∈Z+)个主理想的交是有限生成的．

证明 设R是拟凝聚的，a1，a2，…，an∈R－0，则

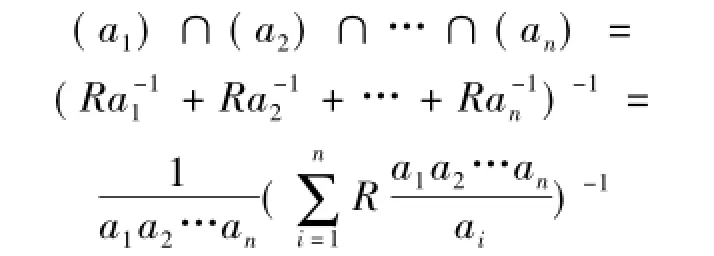
是有限生成的．

反之，设R的任意n个主理想的交是有限生成的，且I=Ra1+Ra2+…+Ran是R的非零有限生成理想，则

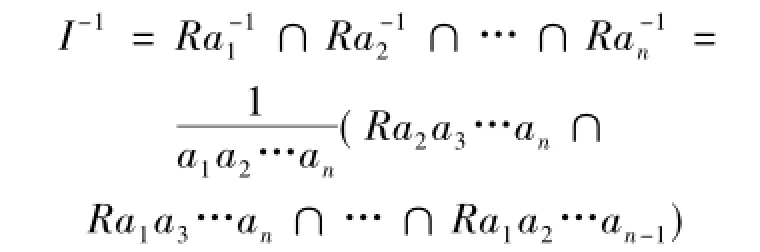
是有限生成的，故R是拟凝聚的．

3 FC整环与拟凝聚整环的w－拓展

对任意星型算子*，M．Fontana等［10］引入了* －凝聚整环的概念，但一般的* －凝聚整环无法对无挠模进行刻划，而王芳贵［5］引入的w－凝聚整环则克服了此问题，且在文献［5，11］中得到了w－凝聚整环与凝聚整环相对应的结果．在文献［11］中，FC整环也得到了w－拓展．所谓的WFC整环，是指对任意x∈K－0，(R:x)={r∈R|rx∈R}都是R的有限型理想．尽管文献［11］对WFC整环进行了研究，但尚未讨论其对应于FC整环的凝聚性(见本文定理2．2)．此外，拟凝聚整环还未得到w－拓展，本节将对它们进行细致的刻划．

引理3．1 设R是整环，A、B是无挠R－模，f:A→B是满同态．若A是有限型的，则B也是有限型的．

证明 设A是有限型的，则存在A的有限生成子模A'，使得Aw=A'w．记B'=f(A')，则B' f(A) =B是B的有限生成子模．下证BwB'w，从而Bw= B'w，即B是有限型的．

设x∈Bw，则存在J∈GV(R)，使得Jx B．由于f是满同态且Jx是有限生成的，故存在A的有限生成子模A″，使得f(A″)=Jx．又A″ A Aw=A'w，故存在J'∈GV(R)，使得J'A″ A'．于是J'Jx= J'f(A″)=f(J'A″) f(A')=B'，从而x∈B'w，因此，BwB'w．

定理3．2 设R是整环，A、B是无挠R－模，f: A→B是同构，则有:

1)A是有限型的当且仅当B是有限型的;

2)A是w－模当且仅当B是w－模．

证明 1)由引理3．1可得．

2)先设A是w－模．设 y∈Bw，则存在J∈GV(R)，使得Jy B，且有，其中S=R－0．记y=，其中b∈B，s∈S．对任意d∈J，由dy∈B可得dy=，其中b'∈B．由于f是满同态，故存在a，a'∈A，使得

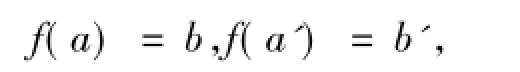
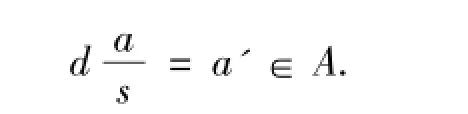
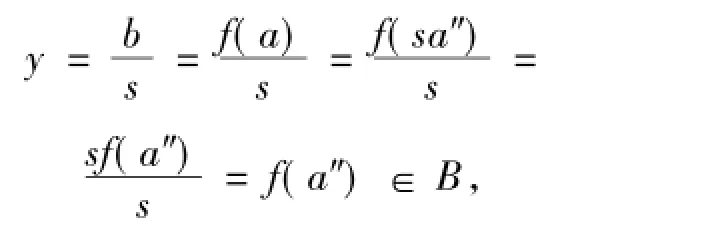
于是BwB，故有Bw=B，即B是w－模．

反之，设B是w－模．由于 f－1:B→A也是同构，故同理可证A是w－模．

定理3．3 对整环R，以下各条件等价:

1)R是WFC整环;

2)R的任意2个主理想的交是有限型的;

3)R的每个2－生成理想是有限表现型的;

4)每个2－生成无挠模是有限表现型的．

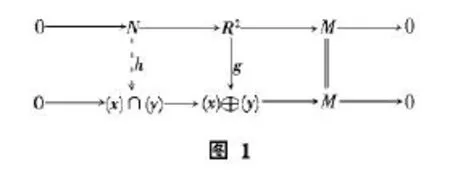
由文献［2］的定理2．4．6，存在h:N→(x)∩(y)，使得左边方图成为交换图，显然g是同构，从而由文献［2］的定理2．4．1，h也是同构．由于(x)∩(y)是有限型的，故由定理3．2，N也是有限型的．因此，由文献［5］的定理2．1，M是有限表现型的．

4) 3)显然．

推论3．4 设R是整环，则R是WFC整环当且仅当对任意a，b∈R－0，(a，b)－1是有限型的．

证明 由(a，b)－1=(a)∩(b)及定理3．3即得．

下面引入拟凝聚整环的w－拓展，并给出其相应的等价刻划．

定义3．5 设R是整环，若对R的每个非零有限生成理想I，I－1是有限型分式理想，则称R是w－拟凝聚整环．

定理3．6 对整环R，以下各条件等价:

1)R是w－拟凝聚整环;

2)R的任意n(n∈Z+)个主理想的交是有限型的;

3)设0→A→F→B→0是正合列，其中rank(A) =1，F是有限生成自由模，且B是无挠模，则A是有限型的．

证明 1) 2)根据定义3．5，类似于定理2．3可证．

1) 3)取对偶模，可得正合列0→B*→F*→C→0，其中C是对应的上核，从而有图2所示行为正合列的交换图．

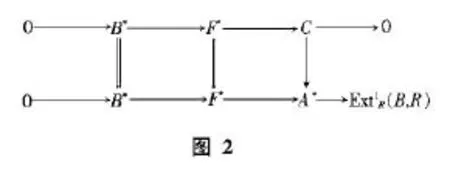
于是由文献［2］的定理2．4．1，C→A*是单同态．由文献［2］的定理2．9．2与例3．4．7有

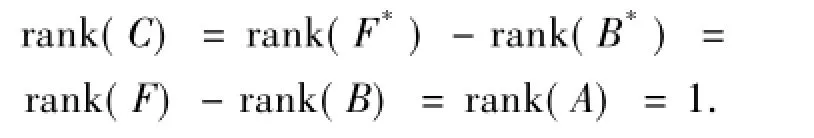
因此，C是秩为1的有限生成无挠模，故可将C嵌入R，即可将C看作R的非零有限生成理想．再取一次对偶模，可得图3所示行为正合列的交换图．

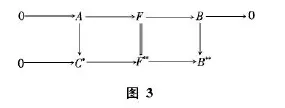
由文献［2］的定理3．4．10，B→B＊＊是单同态，再由文献［2］的定理2．4．1，A→C*C－1是同构，于是由定理3．2，A是有限型的．

3) 1)设I是R的非零有限生成理想，则有正合列0→A→F→I→0，其中F是有限生成自由模，于是又有正合列0→I－1→F*→B→0，其中B A*是无挠模，故I－1是有限型的，因此，R是w－拟凝聚整环．

参考文献

［1］WANG F G，MCCASLAND R L．On w－modules over strong Mori domains［J］．Commun Algebra，1997，25(4):1285－1306．

［2］王芳贵．交换环与星型算子理论［M］．北京:科学出版社，2006．

［3］GILMER R．Multiplicative Ideal Theory［M］．New York:Marcel Dekker，1972．

［4］WANG F G，MCCASLAND R L．On strong Mori domains［J］．J Pure Appl Algebra，1999，135(2):155－165．

［5］王芳贵．有限表现型模和w－凝聚环［J］．四川师范大学学报(自然科学版)，2010，33(1):1－9．

［6］张俊，王芳贵．几类w－模的Krull－Remak－Schmidt定理［J］．四川师范大学学报(自然科学版)，2011，34(5):601－604．

［7］赵松泉，王芳贵，陈翰林．交换环上的平坦模是w－模［J］．四川师范大学学报(自然科学版)，2012，35(3):364－366．

［8］乔磊，王芳贵．w－模范畴上的2个函子及其应用［J］．四川师范大学学报(自然科学版)，2015，38(4):481－486．

［9］YIN H Y，WANG F G，ZHU X S，et al．w－Modules over commutative rings［J］．J Korean Math Soc，2011，48(1):207－222．

［10］FONTANA M，PICOZZA G．Prüfer －multiplication domains and －coherence［J］．Ricerche di Matematica，2006，55: 145－170．

［11］王芳贵．Milnor方图中的w－凝聚性［J］．数学学报，2012，55(1):65－76．

The w-coherence over Domains

YIN Huayu， CHEN Youhua

(College of Mathematics and Software Science，Sichuan Normal University，Chengdu 610066，Sichuan)

In this paper，we discuss carefully the relevant w-coherence over domains by utilizing w-operation theory and with the supplement of torsion-free modules．It is proved that an integral domain R is a WFC domain if and only if the intersection of two principal ideals of R is of finite type，if and only if every two generated ideal of R is of finitely presented type，if and only if every two generated torsion-free R-module is of finitely presented type．Moreover，we introduce the w-expansion of quasicoherent domains and show the equivalent descriptions about it．

w-operation;coherent domain;WFC domain;w-quasicoherent domain

O153．3

A

1001－8395(2016)05－0639－04

10．3969/j．issn．1001－8395．2016．05．004

(编辑 郑月蓉)

2015－05－20

国家自然科学基金(11171240)、教育部博士点基金(20125134110002)和四川省教育厅科研基金(14ZB0035和15ZB0030)

尹华玉(1982—)，女，讲师，主要从事交换环与星型算子理论的研究，E－mail:hyyin2010@163．com

2010 MSC:13A15;13G05