一种基于子矩阵灰阶回代的亚像元分解与增强方法

王 艳 霞,龙 晓 敏,丁 琨,周 汝 良

(1.西南林业大学云南生物多样性研究院，云南 昆明 650224；2.云南农业大学水利学院，云南 昆明 650224；3.西南林业大学理学院，云南 昆明 650224；4.西南林业大学生态旅游学院，云南 昆明 650224)

一种基于子矩阵灰阶回代的亚像元分解与增强方法

王 艳 霞1,龙 晓 敏2,丁 琨3,周 汝 良4*

(1.西南林业大学云南生物多样性研究院，云南 昆明 650224；2.云南农业大学水利学院，云南 昆明 650224；3.西南林业大学理学院，云南 昆明 650224；4.西南林业大学生态旅游学院，云南 昆明 650224)

从任意显示图像的可视化需求出发，针对普通插值法存在的马赛克效应、信息丢失及图像模糊的问题，该文提出了一种基于子矩阵灰阶回代的亚像元分解与增强方法。该方法以分解前图像为回代的子矩阵，将普通内插与子矩阵灰阶回代协同处理，通过对数字图像进行一次亚像元分解后，同步回代分解前图像的中心像元灰阶(子矩阵灰阶回代)，再经多次插值分解、回代、平滑和拉普拉斯增强处理，得到目标像元大小的亚像元分解与增强图像。以DEM、Landsat TM影像、Google Earth发布的影像等为实例，分解和增强后的可视化结果表明，该方法在数字图像放大时，不仅能解决马赛克效应和图像模糊问题，还可提高图像的可视化水平和图像的可读性。

子矩阵；灰阶回代；亚像元分解；图像增强

0 引言

数字图像亚像元分解及增强处理一直是图像研究和应用中的热点和难点问题[1-4]。当前，大多数基于Internet的遥感影像或地图浏览、位置服务系统，在显示大比例尺图像时均存在马赛克效应，以及因内插处理而产生的图像虚化问题。随着计算机硬件和软件技术的快速发展，卫星遥感图像可以通过手机、汽车导航系统、掌上电脑或其他便携式电子设备，实现以可视化为主的专题遥感应用及大众化应用[5,6]。因而，迫切需要一种快速、有效的亚像元分解及增强方法，能将数字图像无级放大且使原始图像信息保持较小程度的丢失。

常用的插值法，如最近邻域法、双线性内插法、立方卷积内插法，虽能缩小图像显示的像元尺寸，但仍没有解决马赛克效应问题。若图像被反复插值会产生严重的信息平滑、丢失等图像模糊问题。因此，有学者认为插值法将会逐渐淡出研究热点[7]，但是仍有部分学者继续探寻各种切实可行的插值方法。曹丽丽等[8]基于常用插值法提出了抗混叠滤波器的内插算法，并取得了较好的实验效果。Li等[9]通过调整低分辨率与高分辨率图像之间的方差，提出了一种基于边缘指导的内插算法，减小了内插算法的复杂度，提高了细节保持能力。Tom等[10-12]提出了EM算法，但该算法计算复杂性高，配准结果误差相对较大。由于插值法处理速度快、实时性好，特别适用于应用前端的动态、可视化图像处理。例如，著名的谷歌地图(Google Earth)仍然使用插值计算方法处理卫星影像的前端实时显示，但是其被无级放大显示时会出现图像虚化、信息丢失等可视化问题。

除了插值法，超分辨率图像重建方法是图像复原、增强的另外一种方法，已被广泛应用于数字电视、医学、军事、遥感等领域[13,14]。基于重建约束和基于学习的两大超分辨率图像重建方式，因信息增强和细节表达需要其他数据辅助，多用于多序列的图像或者单幅图像与训练样本图像之间的信息互补[15,16]。传统的正则化方法可用于解决超分辨率图像复原的病态问题，但是没有考虑图像的空间局部特征，且采用的正则化参数也是全局性的参数，会造成图像细节的模糊或伪信息的残留[17]。为此，有学者提出了基于自适应、自学习、PDE等正则化的超分辨率重建方法[17-19],可从整体或区域图像中获取辅助信息求解所需参数，却不能直接支持服务器端实时快速的分块索引(如金字塔索引)。正如Google Earth，其未采用正则化的超分辨率重构复原技术，仍使用动态内插法完成遥感图像的实时显示。与插值法比较，这些方法实现过程过于复杂，均不能有效支持数字图像压缩和网络传输的技术要求，同时也不能满足用户前端的快速显示需求。

综上，针对普通插值法处理速度快、实时性好，但却易使亚像元图像细节丢失、像元灰阶平均化的问题，本文以“单一数据”的亚像元分解和图像增强为目标，提出了一种简单有效的普通双线性内插或立方卷积内插与子矩阵灰阶回代协同处理的方法。

1 亚像元分解方法简述

以单波段数字图像为例，具体流程为(图1)：使用普通内插法对数字图像进行一次亚像元分解后，同步回代分解前图像的中心像元灰阶(子矩阵灰阶回代);然后对图像进行平滑处理，经多次插值分解、回代以及图像平滑，得到预定义像元大小的亚像元分解图像;最后对图像做增强处理。

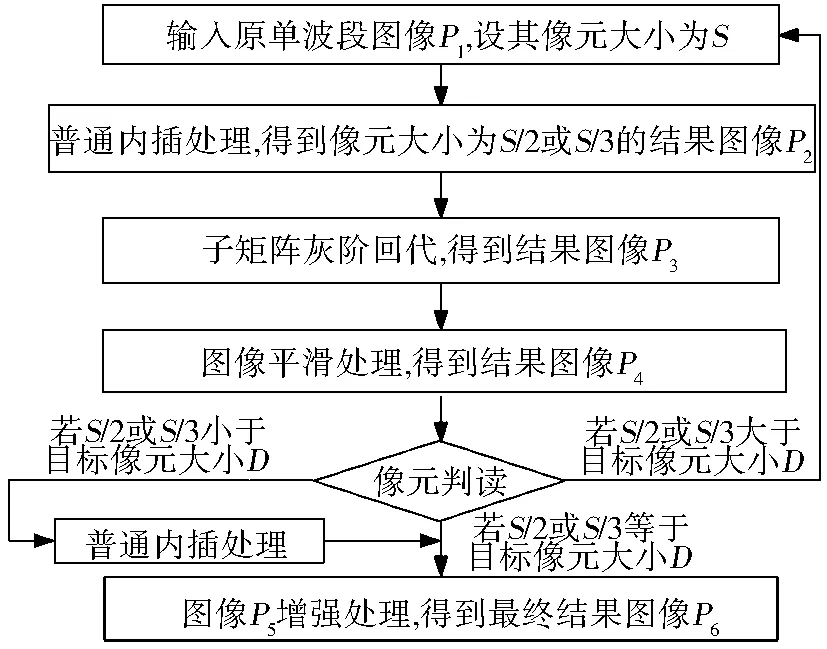
图1 亚像元分解与增强方法流程

1.1 普通内插处理

对原单波段图像P1进行双线性内插[20]或立方卷积内插[21,22]，一般为2×2、3×3分解方式。设P1像元大小为S，普通插值分解后的图像为P2，则2×2分解后P2像元大小为S/2,3×3分解后P2像元大小为S/3。

1.2 子矩阵灰阶回代

数字图像的计算机存储形式是数字矩阵，原图像在整个分解过程中即为子矩阵。用子矩阵某行某列数值替换插值后数字矩阵中某行某列的数值，即为子矩阵灰阶回代。如图2中，子矩阵图像某行某列像元以灰色线条填充。当2×2分解时，子矩阵某行某列像元被1分为4，将分解后的4个亚像元中的右下角像元的灰度值替换为子矩阵图像中所对应行列的灰度值，其余3个亚像元灰度值仍取插值后的值；当3×3分解时，子矩阵图像某行某列像元被1分为9，将分解后的9个亚像元的中心像元灰度值替换为子矩阵图像中所对应行列的灰度值，其余8个亚像元灰度值仍取插值后的值。

设原图像P1大小为n行、m列，则经2×2或3×3分解后的图像P2大小为2×n行、2×m列或3×n行、3×m列。当2×2分解替换时，P1灰阶值替代P2偶行偶列完成子矩阵灰阶回代，得到图像P3。当3×3分解替换时，P1灰阶值替代P2中3×3区域中心位置上像元的灰阶值完成子矩阵灰阶回代，得到图像P3。具体实现算法如下：

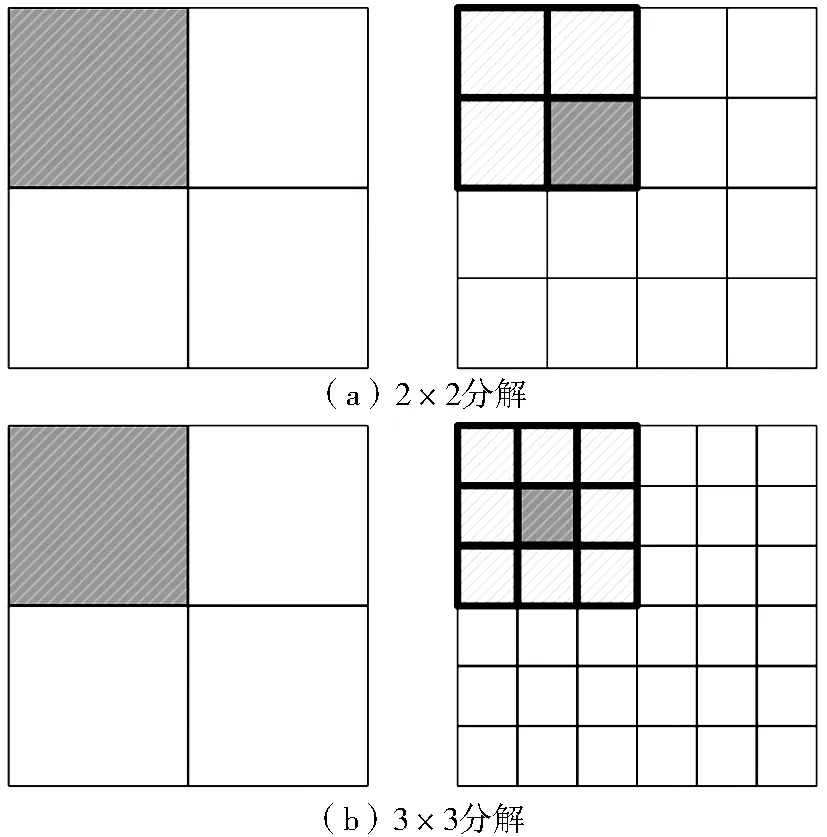
图2 子矩阵像元回代示意

设i，j为子矩阵i行j列，则i= 1，2，3，…，n；j= 1，2，3，…，m。执行二重循环，其中i从1到n，步长为1；j从1到m，步长为1。2×2分解替换时，将P1每个像元灰度值A(i,j)赋值给图像P2的2倍行列点上的像元B(2×i,2×j)，得到新图像P3。3×3分解替换时，将P1对应的矩阵行列值A(i,j)赋值给图像P2对应的行列点B(3×i-1,3×j-1)，得到新图像P3。

1.3 图像平滑处理

子矩阵回代像元的灰阶与周边邻域像元灰阶可能有一定的差异。为减小灰阶跳跃产生的图像不连续问题，还需做平滑处理。本文使用空间域的低通滤波，对P3进行平滑处理，得到P4。低通核如下：

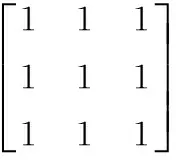
(1)

1.4 像元大小判断

2×2或3×3分解替换方式，可连续地单独或自由组合使用。规定目标像元大小为D，比较交替使用2×2或3×3分解方式后S′与D的大小。若S′大于D，则将P4视为P1，再次进行普通插值、子矩阵灰阶回代及平滑操作；若S′小于D，则再次使用双线性内插等普通插值法对P4进行处理，使插值后图像的像元大小为D；若S′等于D，亚像元分解结束。

1.5 图像增强处理

设亚像元分解后的结果图像为P5，使用各向同性微分算子—拉普拉斯算子对图像P5进行增强处理，得到亚像元分解与增强的结果图像P6。一个二元图像函数f(x,y)的拉普拉斯数学变换定义为[23]：

(2)

拉普拉斯增强本质是基于二阶微分的图像增强。由于拉普拉斯是一种微分算子，其应用会突出图像纹理结构，使模糊的图像清晰化。它将产生一幅把图像中的浅灰色边线和突变点叠加到暗背景中的图像。将原始图像和拉普拉斯图像叠加，可保护拉普拉斯锐化处理的效果，同时又能复原背景信息[23]。使用拉普拉斯变换增强图像的数学表达式为：

(3)

其中，g(x,y)为拉普拉斯变换后的增强图像。

1.6 彩色图像的亚像元分解与增强

若待分解和增强的图像为一般彩色图像，即P1至少包含3个彩色分量，分别记为P11，P12，P13，…，P1i(i≥3)，则亚像元分解和增强方式是分别将P11，P12，P13，…，P1i视为1.2节中的P1，重复上述步骤。若待分解和增强的数字图像为具有L个波段的遥感图像，则将遥感图像的每个波段视为P1，重复上述步骤L次，然后对每个分量进行多波段合成，得到最终的亚像元分解和增强后的彩色图像。

2 亚像元分解实例与增强结果分析

(1)基于DEM。以30m像元的DEM为源数据，使用双线性内插法和本文方法将像元分解为5m大小的DEM，做立体效果渲染后的结果如图3所示。双线性内插法分解后的图3a和亚像元分解后的图3b显示比例尺相同，但后者可视化效果得到了显著改善，明显去除了马赛克效应，且图像较清晰。

图3 采用两种方法的亚像元分解与增强结果对比

(2)基于Landsat TM影像。对地观测数据通常以假彩色模式显示，是一种反立体视觉效果的“负立体”图像，即肉眼观测图像获取的地形信息呈现与实际地形相反的立体视觉，且立体效应不明显，可视性差。如图4a所示，Landsat TM原始影像(30 m 分辨率)经ArcMap软件“Zoom In”工具放大显示后存在明显的马赛克效应，判读难度较大。基于本文提出的方法，对Landsat TM影像做亚像元分解与增强，分解后图像的分辨率为5 m，然后对该图像做正立体处理，如图4b所示。经过正立体处理后，将原始负立体影像图4a中肉眼观测为凹陷地形的像元显示为与真实地表一致的凸起地形。同时，与图4a相比，利用本文方法得到的结果不仅没有马赛克效应，而且明显增加了卫星图像的可读性和可视性。例如，从图4a中很难判读出A、B、C点地物的属性，而从图4b中可判读出A、B点为小山体的山顶，C点可能为山坡。

图4 亚像元分解与增强结果同原始Landsat TM影像对比

(3)基于Google Earth影像(图5，彩图见封2)。图5a为Google Earth显示的2000年云南省安宁市某处的卫星影像，其分辨率较粗，比例尺放大至1∶5 000左右时，因Google Earth可能使用了一种线性的动态内插技术使图像趋向均匀化。以图5a为数据源，结合本文方法制作产生的正立体影像图(图5b)，其像元大小被分解为1 m。相同比例尺显示时，目视判读发现，图5b更加清晰，图像细节丰富，可视化效果明显变好。另外，图5b将图5a中的负立体地形转换成了正立体地形，加强了地形显示。例如，图5a中显示为凹陷的山坡和山顶，在图5b中显示为凸起地形；而在图5a中显示为凸起地形的沟谷区域，在图5b中显示为凹陷地形。图5c为从Google Earth 中随意截取的某地区1 m高分辨率卫星图像，其显示为负立体地形效果。结合本文方法对该图进行处理，可得图5d正立体地形显示效果。对比两图发现，虽然空间分辨率同为1 m，但是结合本文方法，对影像进行地形去除、分解和复原重构后的结果清晰度较高，图像的可判读性更佳，同时沟谷、道路等地形显示为符合真实地貌特征的低洼地形。

图5 亚像元分解与增强结果同原始Google Earth影像对比

(4)基于美国SRTM1(图6，彩图见封2)。对比图6a、图6b发现，将美国SRTM1原始数据(30 m分辨率)分解为3 m空间分辨率，做立体效果渲染后，相同比例尺显示时可视化效果得到明显改善。同时，分解后的图6b并未因使用平滑处理而降低了图像的可视程度，原图(图6a)中的高频信息仍然被保留下来。例如图6a中的山峰、沟谷信息，不仅被保留下来，而且在图6b中被识别的难度明显降低。另外，3 m分辨率立体可视地图(图6c)从1∶10 000放大至以1∶2 000比例尺显示时(图6d)，即使放大5倍，图6d并未出现常见的虚化、马赛克效应问题。

图6 基于美国SRTM1数据的亚像元分解与增强结果

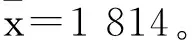
图7 亚像元分解前后的DEM直方图

3 结论与讨论

本文提出了一种基于子矩阵回代的亚像元分解与增强方法，通过灰阶回代使原始图像的所有信息保留在分解后的图像之中，实现了基于“单一数据”，无级放大数字图像的同时保持原始图像信息，有效地增加了亚像元图像的可视化水平和判读能力。该方法利用了普通内插法处理速度快、适用于前端实时显示应用的特点，弥补了其平滑图像的问题，因此可满足遥感图像、地图等数字图像的前端任意比例尺的实时显示需求。

本文分别以DEM、Landsat TM影像、Google Earth影像及美国SRTM1数据为例，展示了亚像元分解和图像增强处理方法的有效性。实例研究表明本文方法可解决中低分辨率卫星影像因放大显示时较明显的马赛克效应及判读难度较大的问题；结合本文方法可解决多次平滑造成灰阶趋向一致化及信息丢失的问题；同时本文方法不仅能较好地保留图像的高频信息，还实现了不同比例尺下的高质量显示。由于亚像元图像的多数像元均通过内插得到，而内插像元本质上是原图像像元的某种平均，这会造成局部区域不同程度的平滑化。所以，需要使用图像增强方法，以突出图像的可视效果。

通过编码，本文方法既可应用于遥感数字图像处理、地图图像处理，也可应用于一般的计算机图像处理[25]。由于亚像元分解的窗口一般为2×2或者3×3像元大小，因此本方法支持服务器端实时快速的分块索引。配合时间序列图像，也可进行超分图像重构和处理。亚像元分解会使图像的数据量呈几何级数增长，影响存储、访问、调用和网络传输的效率。对于专用的图像处理和显示系统，可基于本文方法编码成前端应用系统的插件或专用阵列处理器，在图像显示之前以硬件方式完成亚像元分解和增强处理。

从数字矩阵的相关理论看，分解前的原图像可看成分解后图像的子矩阵，这样灰阶回代的像元是原图像的所有像元。以3×3分解方式为例：每个3×3窗口中心点像元的灰阶是原图像灰阶，其余8个像元是普通内插的结果。这样，虽然多次分解，但是通过回代传递，原图像的所有信息被保留下来。如果每次分解都将原始图像灰阶回代，亚像元图像中将永远保留原始图像信息。但是，由于回代灰阶与周边邻域灰阶可能有较大差异，所以一般还需消除这种灰阶跳跃性。为使分解图像的灰阶与回代像元之间的灰阶跳跃更小，每次亚像元分解回代的灰阶来自上一步的结果图像，而不总是最原始图像。如何改进本文方法，在保持灰阶回代总是来自最原始图像的同时，解决灰阶跳跃可能较大的问题，是需要进一步研究的内容。

[1] YONG G.Sub-pixel land-cover mapping with improved fraction images upon multiple-point simulation[J].International Journal of Applied Earth Observation and Geoinformation,2013,22:115-126.

[2] ATKINSON P M.Super-resolution target mapping from soft classified remotely sensed imagery[J].Photogrammetric Engineering and Remote Sensing,2001,71(7):839-846.

[3] 凌峰,吴胜军,肖飞,等.遥感影像亚像元定位研究综述[J].中国图象图形学报,2011,16(8):1335-1345.

[4] BLASCHKE T,LANG S,LORUP S,et al.Object-oriented image processing in an integrated GIS/remote sensing environment and perspectives for environmental applications[J].Environmental Information for Planning,Politics and the Public,2000(2):555-570.

[5] ZHANG Z H,MOORE J C.Mathematical and Physical Fundamentals of Climate Change[M].Amsterdam:Elsevier,2015.

[6] 邬伦,刘瑜,马修军,等.地理信息系统-原理、方法和应用[M].北京:科学出版社,2001.

[7] THVENAZ P,BLU T,UNSER M,et al.Handbook of Medical Image Processing[M].Orlando:Academic Press,2000.

[8] 曹丽丽,戎蒙恬,刘文江.Scaler中图像缩放内插算法的抗混叠优化[J].信息技术,2009(11):1-4.

[9] LI X,ORCHARD M T.New edge-directed interpolation[J].IEEE Transactions on Image Processing,2001,10(10):1521-1526.

[10] TOM B C,KATSAGGELOS A K.Reconstruction of a high-resolution image by simultaneous registration,restoration and interpolation of low-resolution images[J].Proceedings of the IEEE International Conference on Image Processing,2003,3:539-542.

[11] TOM B C,KATSAGGELOS A K,GALATSANOOS N P.Reconstruction of a high resolution image from registration and restoration of low resolution images[J].Proceedings of the IEEE International Conference on Image Processing,1994(3):553-557.

[12] TOM B C,KATSAGGELOS A K.Reconstruction of a high-resolution image by simultaneous registration,restoration and interpolation of low-resolution images[A].Image Processing,1995[C].International Conference on IEEE,1995，2:539-542.

[13] BOUCHER A,KYRIAKIDIS P C.Super-resolution land cover mapping with indicator geostatistics[J].Remote Sensing of Environment,2006,104(3):264-282.

[14] 林皓波,柏延臣,王锦地,等.遥感影像超分辨率制图研究进展[J].中国图象图形学报,2011,16(4):495-502.

[15] BOSE N K,KIM H C,VALENZUELA H M.Recursive implementation of total least squares algorithm for image reconstruction from noisy,under sampled multiframes[A].Acoustics,Speech and Signal Processing,Minneapolis[C].IEEE International Conference on Acoustics,Speech,and Signal Processing,1993,5:269-272.

[16] TATEM A J,LEWIS H G,ATKINSON P M,et al.Super-resolution target identification from remotely sensed images using a Hopfield neural network[J].IEEE Transactions on Geoscience & Remote Sensing,2011,39:781-796.

[17] 谢琦,陈纬义.基于自适应正则化的超分辨率重建方法[J].强激光与粒子束,2014,26(10):88-94.

[18] 李娟,吴谨,陈振学,等.基于自学习的稀疏正则化图像超分辨率方法[J].仪器仪表学报,2015,36(1):194-200.

[19] 陈远旭,罗予频,胡东成.基于PDE正则化的超分辨率图像重构方法[J].计算机工程,2007,33(22):4-5.

[20] 米慧超,张小娣,赖锴.基于ENVI软件的遥感影像内插方法偏差改正[J].计算机科学,2014,41(8):322-326.

[21] 梅安新,彭望琭,秦其明,等.遥感导论[M].北京:高等教育出版社,2002.

[22] 卓静,邓凤东,李登科,等.陕北地区TM影像重采样方法研究[J].陕西气象,2003(4):17-20.

[23] RAFAEL C G,RICHARD E W.阮秋琦,阮宇智,等(译).数字图像处理[M].北京:电子工业出版社,2007.

[24] 阳正熙,吴堑虹,彭直兴,等.地学数据分析教程[M].北京:科学出版社,2008.

[25] 黄诚,王皓,王一凯,等.基于亚像元分解与增强的MODIS卫星林火监测图像制作[J].西部林业科学,2015,44(1):82-87.

Sub Pixel Decomposition and Enhancement Based on Back Substitution of Grey Scale Values in the Sub-Matrix

WANG Yan-xia1,LONG Xiao-min2,DING Kun3,ZHOU Ru-liang4

(1.YunnanAcademyofBiodiversity,SouthwestForestryUniversity,Kunming650224;2.CollegeofWaterConservancy,YunnanAgriculturalUniversity,Kunming650224;3.FacultyofScience,SouthwestForestryUniversity,Kunming650224;4.FacultyofEcotourism,SouthwestForestryUniversity,Kunming650224,China)

From the perspective of meeting the need of the random image visualization,this paper proposed a method of sub-pixel decomposition and enhancement based on back substitution of grey scale values in the sub-matrix.The method was for solving some problems of ordinary interpolation methods when displaying images in a large scale,such as mosaic effect,information loss and image blurring.The study considered a pre-decomposition image as one sub matrix.After decomposing by one of ordinary interpolation methods,the central pixels of the decomposed image were substituted by the grey scale values in the sub-matrix.Specifically,once digital images were done decomposition,the pixels of the sub-matrix were substituted back.Thus,interpolation and decomposition,substitution back were looped for many times until the image with the targeting sub-pixel resolution was attained with cooperative processing of image smoothing and enhancement by Laplace Transform.With the application examples of DEM(Digital Elevation Model),images of Landsat TM,Google Earth,etc.,the results showed that the method solved the problems of ordinary interpolations,effectively improved the level of image visualization and increased the readability of remote sensing images.

sub matrix;back substitution of grey scale values;sub pixel decomposition;image enhancement

2015-11-24；

2016-05-30

国家林业公益性行业科研专项项目(201404402)；云南省科技创新人才计划项目(2014HC014)；云南省教育厅资助项目(2015Z135)；国家自然科学基金项目(41261085)

王艳霞(1982-)，女，博士，助理研究员，研究方向：林业遥感、数字生态系统研建。*通讯作者E-mail:zhou_ruliang@163.com

10.3969/j.issn.1672-0504.2016.06.003

TP751.1

A

1672-0504(2016)06-0012-06