小比例尺多尺度居民地面/面目标几何不一致性探测方法
2016-06-05温伯威,马京振,马超
温 伯 威,马 京 振,马 超
(信息工程大学,河南 郑州 450052)
小比例尺多尺度居民地面/面目标几何不一致性探测方法
温 伯 威,马 京 振,马 超
(信息工程大学,河南 郑州 450052)
不一致性探测是多源空间数据集成与融合、空间数据变化检测与更新、多尺度地理信息数据一致性维护的重要环节。居民地作为现实世界中变化最活跃的地理要素之一,其在多尺度地理信息数据库中表现出来的几何不一致性问题十分突出。在分析多尺度居民地面/面目标几何不一致性根源的基础上,将多尺度居民地面/面目标几何不一致分为实体表达状态不一致和实体表达形态不一致。提出了利用实体表达状态差异、空间位置差异、形状差异、大小差异以及面积叠置率探测多尺度同名面状居民地几何不一致性的方法,并给出了具体的实验步骤。实验结果表明,该方法能够识别出不同尺度数据中存在几何不一致性的同名面状居民地,不一致性探测结果可以作为多尺度居民地面/面目标几何一致性处理的依据。
多尺度居民地;同名实体匹配;几何不一致性;空间位置差异;形状差异;大小差异
0 引言
一致性作为评价空间数据质量的重要指标[1],自20世纪90年代以来就吸引了学者的广泛关注[2-4]。空间数据的不一致性主要包括:几何不一致性、语义不一致性及空间关系不一致性。空间关系不一致性又分为方向关系不一致性、距离关系不一致性及拓扑关系不一致性[5,6]。目前,空间数据不一致性研究的对象多为相同尺度或者相近尺度的数据[7,8],研究成果主要集中在拓扑关系不一致性[9-11],多尺度地理信息数据的几何不一致性研究相对薄弱。
长期以来,受制图综合与数据模型等因素的制约,不同尺度空间数据的生产、存储、管理以及更新相互独立,同一地理实体在不同尺度数据中的表达之间缺乏有机联系,直接导致了多尺度地理信息数据的不一致性问题。多尺度地理信息数据之间的不一致性问题不仅严重影响着用户的空间认知,而且会造成地理信息应用的混乱。
不一致性探测是进行多尺度地理信息数据一致性处理的基础和前提,可以为多尺度数据一致性处理提供科学依据。作为现实世界中变化最活跃的地理要素之一,居民地要素在多尺度地理信息数据库中表现出来的几何不一致性问题十分突出。本文以居民地面/面目标为例研究了多尺度地理信息数据的几何不一致性问题,提出了多尺度居民地面/面目标的几何不一致性探测方法。
1 多尺度居民地面/面目标几何不一致性根源及分类
1.1 多尺度地理信息数据几何不一致性
尺度是空间数据的重要特征,反映了数据模拟真实世界的详细程度。对于单一尺度的空间数据,其不一致性是指由于数据表达违背某些约束引起的地理对象之间的矛盾和冲突问题[12]。多尺度地理信息数据几何不一致性是指同一地理实体的几何特征在不同尺度空间数据中的表达之间存在着逻辑矛盾[13]。例如,现实世界中名称为灵井镇的同一居民地在不同尺度空间数据中呈现出明显的几何不一致性(图1)。多尺度地理信息数据之间的几何不一致性问题不仅严重影响着用户的空间认知,而且会造成地理信息应用的混乱。因此,如何发现多尺度地理信息数据之间的不一致性并进行处理一直是数据生产者面临的核心问题。
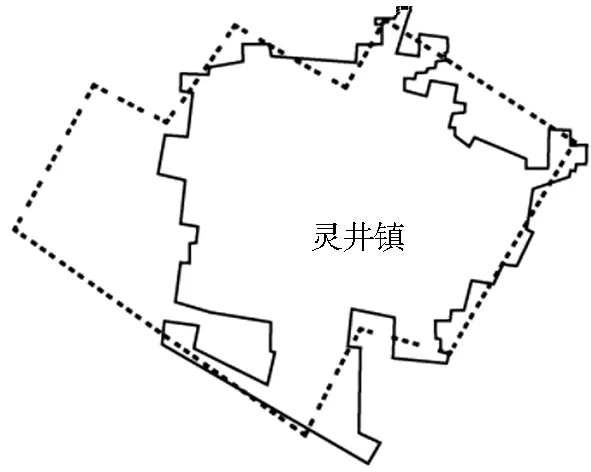
图1 多尺度面状居民地几何不一致性示意
1.2 多尺度居民地面/面目标几何不一致性的根源
居民地在现实世界中发生的真实变化、作业员的经验和水平、资料来源差异、制图综合等因素都可能造成多尺度居民地面/面目标之间的几何不一致性问题。按成因的不同,多尺度居民地面/面目标几何不一致性的根源可以归纳为以下5类:
(2)人类认知能力的局限性。空间数据描述现实世界的准确性受到人类认知能力的制约,尽管当今最先进测量仪器的精度可以达到毫米级别,但人们还是不能获得居民地边界的真值,而不同尺度的居民地数据是在不同的人类认知水平下生产与更新的。
(3)生产与更新资料来源差异。生产与更新不同尺度居民地数据通常采用多种来源的资料,这些资料中的居民地数据在几何精度、现势性等方面存在着较大差异,这些差异是造成多尺度居民地面/面目标几何不一致性的重要原因之一。
(4)制图综合因素。不同尺度空间数据对居民地表达的详细程度不同,在尺度变换中需要对居民地要素进行综合。化简、合并、概括、位移等制图综合操作都会在某种程度上改变面状居民地的几何特征,造成同一面状居民地在不同尺度空间数据表达中存在几何不一致性。
(5)误差因素。在居民地数据获取、采集、处理、使用的各个环节都可能产生误差,而且误差还具有传播性。由于误差因素的存在,同一居民地的几何特征在不同空间数据表达中必然存在偏差。
1.3 多尺度居民地面/面目标几何不一致性分类
依据表现形式的不同,多尺度居民地面/面目标的几何不一致性可以分为以下两类:1)实体表达状态不一致,是指同一居民地在不同尺度空间数据中没有同时表达。例如,某面状居民地在较小比例尺空间数据中存在,在较大比例尺空间数据中消失,这种情况通常是由数据现势性不同造成的。同时,制图综合也会造成实体表达状态不一致,即面状居民地在较大比例尺空间数据中存在,在较小比例尺空间数据中不存在。2)实体表达形态不一致,是指同一居民地的空间位置、面积、周长、形状等几何特征在不同尺度空间数据表达中存在着逻辑矛盾。实体表达状态不一致又可以进一步细分为:实体表达空间位置不一致、实体表达大小不一致、实体表达形状不一致。生产与更新资料来源差异、制图综合因素、误差因素等都可能造成多尺度同名面状居民地的表达状态不一致。
通过上述分析,制图综合是造成多尺度同名面状居民地几何不一致性的主要因素之一。由于制图综合造成的几何不一致性符合数据生产要求和规范,不影响用户的空间认知,不需要处理。因此,本文所指的几何不一致性是非制图综合造成的不一致,即重点探测真实变化、误差等因素导致的多尺度居民地面/面目标几何不一致性。
本研究纳入单纯慢阻肺患者508例,慢阻肺来源ACO 295例,其中ACO错失早期诊断时间为3(1,9)年,相比单纯慢阻肺3(0.5,8)年,两者无明显差异(Z=-1.86,P=0.063)。单纯慢阻肺肺功能FEV1%为53.8%±22.1%,ACO为53.1%±19.9%,两组无统计学差异(t=0.376,P=0.707)。
2 多尺度居民地面/面目标几何不一致性探测
2.1 多尺度居民地面/面目标几何不一致性探测思路
多尺度居民地面/面目标几何不一致性探测的研究对象为同名面状居民地,旨在发现非制图综合因素造成的几何不一致性。多尺度居民地面/面目标几何不一致性探测的思路为:利用实体表达状态差异、空间位置差异、形状差异、大小差异、面积叠置率5个指标检测存在几何不一致性的同名面状居民地。
2.2 多尺度居民地面/面目标几何不一致性探测指标
2.2.1 实体表达状态差异 实体表达状态差异主要用来描述多尺度同名面状居民在实体表达状态方面的不一致性。面状居民地在现实世界的出现、消失以及尺度变换都会引起居民地在多尺度地理信息数据库中表达状态的变化,真实变化与尺度变换造成的实体表达状态差异在本质上是不同的,尺度变换引起的实体表达状态差异是合理的。因此,多尺度居民地面/面目标实体表达状态不一致探测的重点是发现真实变化造成的差异。多尺度居民地面/面目标的表达状态差异可以通过匹配模式判定,如1∶0与0∶1(大比例尺居民地在前)这两类匹配模式下面状居民地的表达状态显然是不同的。
2.2.2 空间位置差异 重心、质心、逻辑中心等都可以反映面状居民地的空间位置。鉴于质心具有不受尺度变换影响等特点,本文采用质心描述面状居民地的空间位置。设P和Q分别为大比例尺和小比例尺面状居民地,如图2所示,Op和OQ分别为P和Q的质心,DPQ为OP和OQ之间的距离,aP与aQ分别为P和Q外接矩形(MBR)的长轴,τD为P和Q的空间位置差异,则τD可表达为:
(1)
当OP与OQ重合时,DPQ等于零,τD等于零,P与Q不存在空间位置差异;DPQ越大,τD越大,P与Q之间的空间位置差异越大。
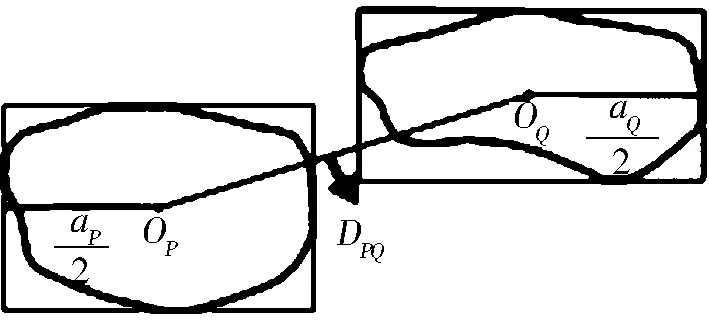
图2 空间位置差异的计算
2.2.3 形状差异 形状是面目标的本质特征之一,是多尺度居民地面/面目标实体表达形态不一致性探测的重要指标。不变矩是面目标的全局形状描述子,具有不随几何变换(旋转、缩放、平移)变化的特点,是一种理想的形状描述子[14]。设m1、m2、m3、m4、m5、m6、m7为面状居民地P的7个矩不变量,n1、n2、n3、n4、n5、n6、n7为面状居民地Q的7个矩不变量,τM为P和Q的形状差异,采用文献[15]中的方法计算矩不变量,则τM可表达为:
(2)
2.2.4 大小差异 大小是面状居民地最直观的特征。周长和面积都可以反映面状居民地的大小,本文采用面积差描述面状居民地的大小差异。设AP和AQ分别为P和Q的面积,τA为P和Q的面积差异,则τA可表达为:
(3)
2.2.5 面积叠置率 面积叠置率是一个综合性探测指标,不仅可以反映同名面状居民地的空间位置差异,还可以反映形状差异和大小差异。设面状居民地P和Q并集的面积为UPQ,IPQ为P和Q交集的面积,则面积重叠率τO为:
(4)
上述5个不一致性探测指标适用的范围和匹配模式有所不同。实体表达状态差异适合探测1∶0与0∶1匹配模式下同名面状居民地的几何不一致性;空间位置差异、形状差异适合探测1∶1匹配模式下同名面状居民地的几何不一致性;大小差异、面积叠置率适合探测1∶1、m∶1、1∶n、m∶n匹配模式下同名面状居民地的几何不一致性。
2.3 多尺度居民地面/面目标几何不一致性探测步骤
多尺度居民地面/面目标几何不一致性探测步骤如下:1)数据预处理。统一的数学基础是进行居民地数据叠置和同名实体匹配的基础,数据预处理主要是为了实现两种尺度面状居民地数据坐标系、投影的统一,采用坐标系和投影变换方法统一两种尺度面状居民地数据的数学基础。2)同名实体匹配。目标的属性信息、几何信息、拓扑信息都可以作为判定多尺度居民地面目标与面目标匹配的依据。当两种尺度下居民地面目标的属性结构相同且属性信息完整时,采用目标的属性信息作为匹配依据,例如,若不同尺度居民地面目标的名称、类型、人口等属性信息相同则判定两者为同名实体;当属性结构不同或者属性信息不完整时,采用目标的几何信息和拓扑信息作为匹配依据。对大比例尺空间数据与小比例尺空间数据中的同名面状居民地以及匹配模式做标记。3)依据匹配模式,计算几何不一致性探测各个指标的值。采用2.2节定义的不一致性探测指标计算方法分别计算同名面状居民地之间的空间位置差异、形状差异、大小差异以及面积叠置率。4)根据指标值判断多尺度居民地面/面目标的几何不一致性。分别比较τD与空间位置差异阈值εD、τM与形状差异阈值εM、τA与大小差异阈值εA、τO与面积叠置率阈值εO之间的大小,当τD、τM、τA中任何一项指标值大于对应阈值或者τO小于εO,即判定多尺度居民地面/面目标存在几何不一致性。
3 实验与分析
为了验证本文提出的多尺度居民地面/面目标几何不一致性探测方法的合理性和科学性,选取同一地区的1∶50万与1∶100万面状居民地数据作为实验对象。1∶50万数据包含70个面状居民地,1∶100万数据包含14个面状居民地。两种数据叠置在一起的效果如图3所示,虚线表示的面目标为1∶100万中的面状居民地,实线表示的面目标为1∶50万中的面状居民地。

图3 实验数据概况
采用文中方法进行同名面状居民地匹配,得到的1∶0、1∶1、0∶1、m∶1、1∶n、m∶n匹配数目分别为50、9、0、3、0、1。根据空间数据生产规范可以得知,在1∶100万数据中图上面积大于12 mm2的居民地采用面状符号表示。分别计算1∶50万数据中属于1∶0匹配模式面状居民地的图上面积,并与12 mm2进行比较。计算结果表明属于1∶0匹配模式面状居民地的图上面积均小于12 mm2。因此,不存在非制图综合因素造成的几何不一致性。
采用空间位置差异、形状差异、大小差异、面积叠置率对1∶1、m∶1、1∶n、m∶n匹配模式下的同名面状居民地进行几何不一致性探测。为了判定1∶1、m∶1、1∶n、m∶n匹配模式下同名面状居民地之间是否存在几何不一致性,需要确定εD、εM、εA、εO的值,如何评估制图综合对多尺度同名面状居民地几何不一致性的影响是确定εD、εM、εA、εO值的关键。由于制图综合对同名面状居民地几何不一致性的影响难以定量化表达,本文根据制图专家经验,分别取10%、15%、15%、85%作为εD、εM、εA、εO的值。对于1∶1匹配模式下的同名面状居民地,若其空间位置差异、形状差异、大小差异有任何一项大于对应阈值或者面积叠置率小于85%,则判定实体表达形态不一致。对于m∶1模式下的同名面状居民地,若其大小差异大于15%或者面积叠置率小于85%,则判定实体表达形态不一致。1∶50万与1∶100万居民地面/面目标几何不一致性的探测结果如表1所示。通过表1分析可以得知,存在几何不一致性的同名面状居民地共有8对,其中包括4对1∶1匹配,3对m∶1匹配,1对m∶n匹配。
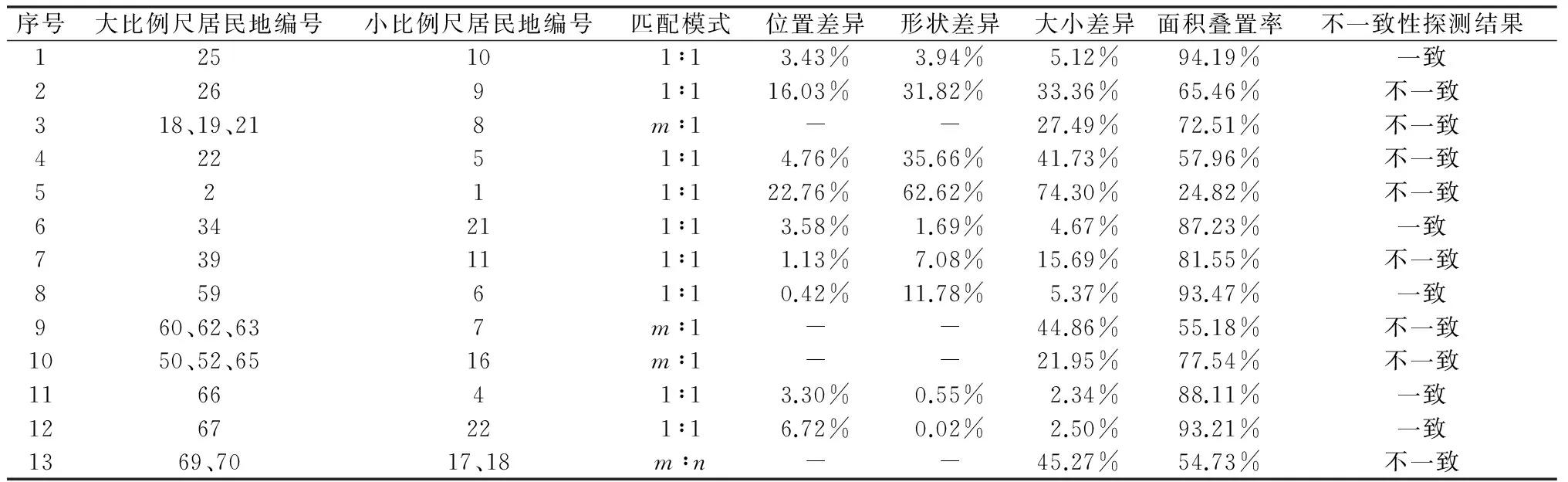
表1 1∶50万与1∶100万同名面状居民地几何不一致性探测结果
为了验证探测结果的可靠性,采取人工方式对多尺度同名面状居民地几何不一致性探测结果进行检验。图4是其中的3组同名面状居民地样本数据,其中图4a、图4b、图4c分别对应着表1中序号为12、2、3的同名面状居民地。从图中可以看出,图4a中的同名面状居民地在不同尺度空间数据中的表达差异是由制图综合造成的;图4b、图4c中的同名面状居民地的大小、形状在不同尺度空间数据中表现出了较大差异,显然,这种差异不是制图综合因素引起的,而是居民地在现实世界的变化没有同步更新至1∶50万、1∶100万空间数据导致的。因此,图4a中的同名面状居民地不存在几何不一致性,图4b、图4c中的同名面状居民地存在几何不一致性。通过比较表1中3组同名面状居民地几何不一致性的探测结果与人工判断结果,可以得出如下结论:1)位置差异、形状差异、大小差异、面积叠置率能够识别出不同尺度数据中存在几何不一致性的同名面状居民地;2)探测结果可以作为多尺度居民地面/面目标几何不一致性处理的依据。
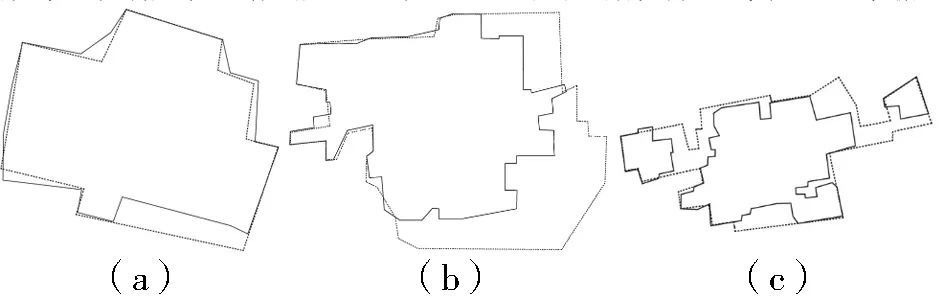
图4 3组同名面状居民地样本数据
4 结论
不一致性探测是多源空间数据集成与融合、空间数据变化检测与更新、多尺度地理信息数据一致性维护的重要环节。本文提出采用实体表达状态差异、空间位置差异、形状差异、大小差异以及面积叠置率探测多尺度居民地面/面目标的几何不一致性,并进行了实验验证。本文提出的几何不一致性探测方法使用的各个阈值是基于制图专家经验确定的,因此,存在一定的主观性和局限性。采用多类型样本数据进行反复实验使阈值的设置更加合理和科学是下一步工作的重点。
[1] KAINZ W.Logical consistency[A].GUPTILL S C,MORRISON J L.Elements of Spatial Data Quality[C].Oxford:Elsevier,1995.109-137.
[2] CORCORAN P,MOONEY P.Planar and non-planar topologically consistent vector map simplification[J].International Journal of Geographical Information Science,2011,25(10):1659-1680.
[3] 郑春燕,胡华科.居民地与道路之间拓扑关系一致性的模糊评价[J].测绘科学,2012,37(1):165-167.
[4] 杜世宏,雒立群,赵文智,等.多尺度空间关系研究进展[J].地球信息科学学报,2015,17(2):135-146.
[5] 简灿良.多比例尺地图数据不一致性探测与处理方法研究[D].武汉:武汉大学,2013.
[6] 朱蕊.一种面向道路要素更新的几何位置一致性处理方法[J].测绘科学技术学报,2014,31(2):191-193.
[7] 詹陈胜,武芳,翟仁健,等.基于拓扑一致性的线目标空间冲突检测方法[J].测绘科学技术学报,2011,28(5):387-390.
[8] GADISH D.Inconsistency Detection and Adjustment of Spatial Data Using Rule Discovery[D].Guelph:University of Guelph,2001.42-59.
[9] 陈佳丽,易宝林,任艳.基于对象匹配方法的多重表达中的一致性处理[J].武汉大学学报(工学版),2007,40(3):115-119.
[10] 王少华,钟耳顺,李绍俊,等.面向矢量数据叠加分析的拓扑一致性处理研究[J].地理与地理信息科学,2015,31(1):12-16.
[11] LIU W Z,CHEN J,ZHAO R L,et al.A refined line-line spatial relationship model for spatial conflict detection[A].Perspectives in Conceptual Modeling[C].Springer Berlin Heidelberg,2005.239-248.
[12]EGENHOFER M.Pre-processing queries with spatial constrains[J].Photogrammtric Engineering & Remote Sensing,1994,60(6):783-970.
[13] SHEEREN D,MUSTIRE S,ZUCKER J.How to integrate heterogeneous spatial databases in a consistent way[A].Advances in Databases and Information Systems[C].Springer Berlin Heidelberg,2004.364-378.
[14] 刘亦书,杨力华,孙倩.轮廓矩不变量及其在物体形状识别中的应用[J].中国图像图形学报,2004,9(3):308-312.
[15] AL-BAKRI M.Developing Tools and Models for Evaluating Geospatial Data Integration of Official and VGI Data Sources[D].Newcastle:Newcastle University,2012.109-114.
Geometry Inconsistency Detection Method of Multi-scale Corresponding Area Habitation for Small Scale
WEN Bo-wei,MA Jing-zhen,MA Chao
(InformationEngineeringUniversity,Zhengzhou450052,China)
Inconsistency detection is an important step of multi-source spatial data integration and fusion,spatial data change detection and updating,and multi-scale spatial data consistency maintenance.As one of the most active change elements in the real world,the geometry inconsistency problem of habitation in multi-scale spatial database is very serious.On the base of analyzing geometry inconsistency root,geometry inconsistency of the same area habitation was divided into entity expression status inconsistency and entity expression shape inconsistency.Geometry inconsistency detection method of the same area habitation was proposed in this paper,which utilized the differences of object′s expression state,spatial location,shape,size and area overlap ratio,and the specific experimental steps were given in this paper.The results showed that this method could recognize the same area habitation that had geometry inconsistency in multi-scale data,and the inconsistency detection results could provide basis for multi-scale corresponding area habitation consistency processing.
multi-scale habitation;same entity matching;geometry inconsistency;spatial location difference;shape difference;size difference
2016-01-27;
2016-05-25
国家自然科学基金项目(41201391、41571399)
温伯威(1986-),男,博士,研究方向为多源空间数据融合、多尺度地理信息数据一致性处理。E-mail:GIS0803@163.com
10.3969/j.issn.1672-0504.2016.06.002
P208
A
1672-0504(2016)06-0007-05
