动态应变场下相移光栅光谱特性及实验研究
2016-06-05王正方隋青美
王正方、王 静、隋青美*
1. 山东大学控制科学与工程学院、山东 济南 250061 2. Nanyang Technological University,Energy Research Institute@NTU,Singapore 639798
动态应变场下相移光栅光谱特性及实验研究
王正方1,2、王 静1、隋青美1*
1. 山东大学控制科学与工程学院、山东 济南 250061 2. Nanyang Technological University,Energy Research Institute@NTU,Singapore 639798
光纤传感技术以其抗电磁干扰、高精度、易组网等优势在航空航天及地下工程领域的声发射传感中得到了广泛应用。针对光纤光栅声发射监测系统、目前研究侧重于均匀光纤光栅的动态应变场传感特性、基于相移光纤光栅(phase-shifted fiber Bragg grating,PS-FBG)这一新型光纤光栅器件、重点研究声发射激励产生的动态应变场下相移光纤光栅的光谱特性变化规律。首先利用传输矩阵理论、建立PS-FBG的动态应变传感模型、利用指数衰减的余弦函数模拟声发射激励产生的动态应变场。通过数值仿真、详细研究PS-FBG光谱对动态应变场幅度、采样时刻、衰减系数、声发射频率及波长的响应特性。结果表明、PS-FBG反射谱形状随声发射频率与采样时刻呈现周期性变化、具体表现为透射窗口所对波长产生周期性漂移、而带宽变化不明显; 随着动态应变场幅值越大、PS-FBG反射谱的谐振峰向两侧逐渐增多、透射窗口所对波长漂移很小; 一定范围内衰减系数对PS-FBG光谱影响较大; 而当声发射波长为0.1~2L时、对PS-FBG光谱产生较大影响、此时光谱畸变较严重、在此范围外、光谱形状不发生明显变化。最后、搭建连续信号激励下的动态应变场实验平台、分析不同幅度a与频率f变化下PS-FBG的光谱特性、实验结果与仿真结果较好吻合。表明PS-FBG光谱对不同声发射激励产生的动态应变场响应不同、呈现一定规律性、该研究为基于相移光纤光栅传感技术的声发射传感提供理论指导。
相移光纤光栅; 动态应变场; 声发射传感
引 言
声发射是金属或岩体等材料在局部区域应力集中作用下产生微破坏、同时快速释放能量并产生瞬态弹性应力波的一种自然现象。目前、基于声发射/微震的监测技术已广泛应用于航空航天工程与地下工程等领域、通过拾取声发射特征信息、有效评估结构损伤程度与煤岩体失稳状态、定位外部扰动及内部微破坏源位置、实现结构寿命评估及工程灾害事故预测[1-2]。基于光纤传感技术的声发射监测是近年来兴起的新型监测技术、与传统的电子式监测技术相比、具有本质安全、抗电磁干扰、防水抗腐蚀、易于组网、材质轻柔易植入的优势、特别适合于航空航天及地下工程等极端环境下的实时监测[3-4]。
光纤布拉格光栅(fiber Bragg grating,FBG)是光纤声发射监测系统中普遍采用的传感元件、在声发射激励产生的动态应变场下光纤光栅的光谱特性是声发射监测技术的基础。庞丹丹分析了声发射激励下、不同长度FBG光谱对声发射信号函数的响应规律[5]; Xia Ming-jun等分析了不同声发射波长及采样时间下均匀光纤光栅的光谱变化[6]; 上述研究均针对均匀周期FBG光谱对声发射信号的响应特性进行研究。在非均匀周期FBG的动态应变场响应研究方面、王静等分析了动态应力场下线性啁啾光纤光栅的光谱响应特性、并获取了LCFBG光谱与动态应变函数的变化规律[7]。相移光纤光栅(phase-shifted FBG,PS-FBG)是一种典型的非均匀周期光纤光栅、它是在均匀光纤光栅栅区特定点引入相移量、从而在其反射谱阻带中打开带宽极窄的透射窗口。这种独特的光谱特性、使其在声发射等动态信号的传感中具有很好的应用前景[8-9]。在相移光栅光谱特性研究领域、光谱研究集中在对温度与均匀应变影响下相移光栅传感特性进行了仿真与实验研究[10-12]; 鲁韶华等对相移量、相移点位置对啁啾相移光栅反射谱的影响进行了仿真与实验分析[13]; 余华清等分析了均匀应变和温度变化下啁啾相移光栅的传感特性[14]; 王正方等分析了非均匀应变场相移光栅的光谱特性。Qi Wu等研究了不同方向及距离声发射源下、相移光纤光栅的波长响应灵敏度[15]。而对于动态应变场特别是声发射信号激励下的动态应变场下相移光栅的光谱特性研究较少。
本文利用传输矩阵法、建立了声发射信号激励产生的动态应变场中相移光纤光栅的传感模型、对声发射信号调制函数各个不同参数下的相移光栅光谱特性进行仿真、分析反射率、透射窗口对应波长、光谱形状等的变化规律、并开展实验验证。本文的研究对相移光纤光栅特别在声发射等动态信号传感领域的推广应用具有重要的指导意义。
1 相移光纤光栅动态应变传感模型
相移光栅的折射率分布如图1所示、栅区轴向某点的折射率突变引起相位变化、相当于两段均匀光纤光栅的无缝级联。假设光栅栅区长度为L、被相移点分成的两段均匀光栅的长度分别为L1和L2。
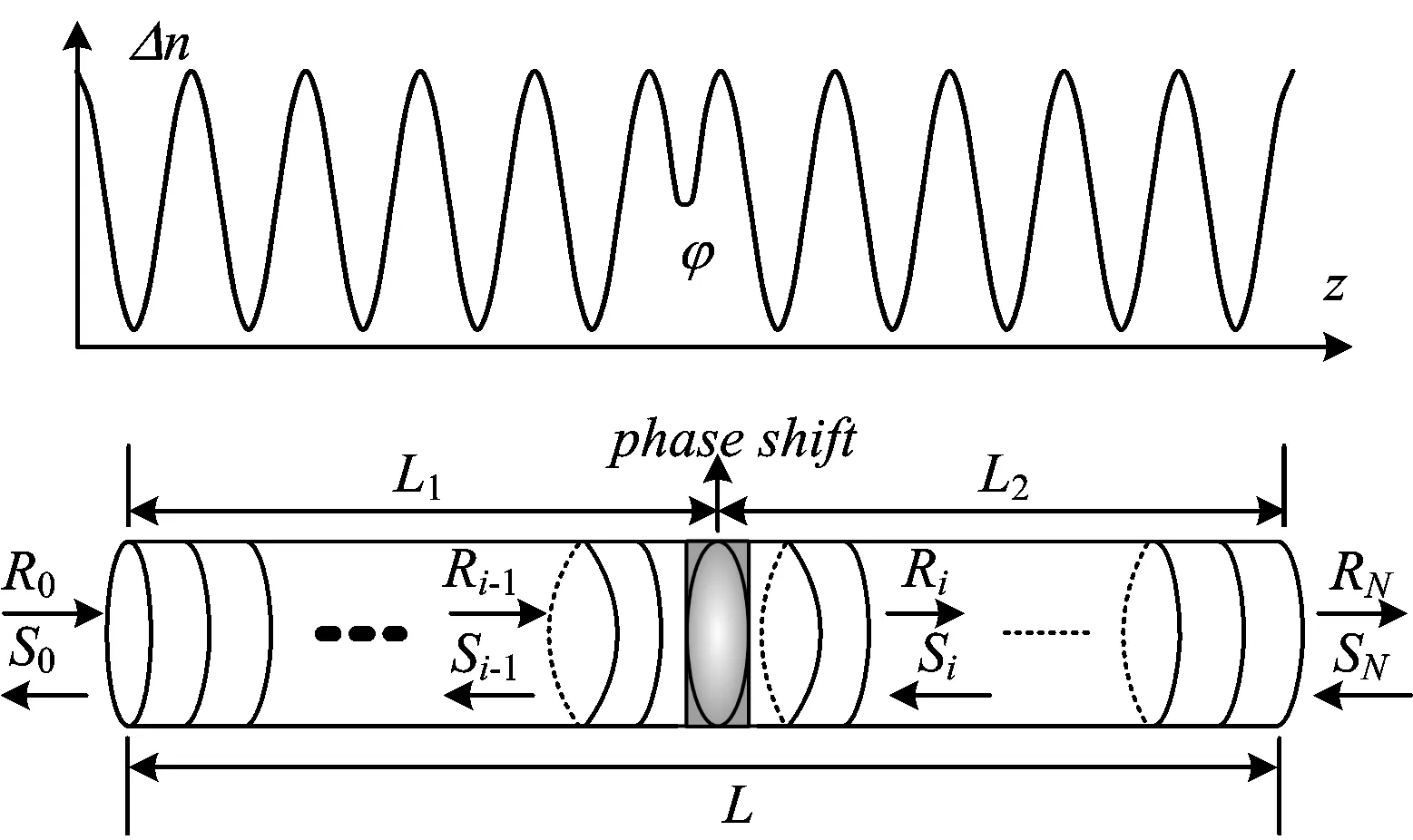
图1 相移光纤光栅传输矩阵模型
将相移光栅栅区在长度方向N等分、每段等效为一均匀周期光纤光栅、根据传输矩阵理论、每段传输特性可表示为一2×2传输矩阵、第i段均匀光栅的传输矩阵为Fi为
Fi=
(1)
(2)
则整个相移光纤光栅的传输矩阵为F=FNFN-1…FiFφFi-1…F1F0。
在声发射信号激励下、相移光纤光栅受动态应变场作用、沿光栅轴向的动态应变场模型可表示为与时间相关的余弦函数ε(z,t)
(5)
式中、0
根据几何效应与弹光效应原理、在动态应变场ε(z,t)作用下、相移光纤光栅周期分布Λ(z,t)与有效折射率分布neff(z,t)分别为
Λ(z,t)=Λ0[1+ε(z,t)]
(6)
(7)
其中P11和P12表示光纤弹光系数、μ为光纤泊松比、Λ0为相移光纤光栅的初始栅格周期。
2 动态应变场下相移光纤光栅光谱仿真
根据传输矩阵法、对不同动态应变分布函数下相移光栅的光谱进行仿真。仿真选用相移光纤光栅相移量φ为π、相移点位于栅区中心、纤芯有效折射率neff为1.459、折射率调制深度δneff为2.6×10-4、栅区长度L为10 mm、栅格周期Λ0为530.858 nm。
2.1 PS-FBG光谱对时间t的响应特性
令频率f=100 Hz、幅值a=100 με、衰减系数b=1、λE=0.5L(L为栅区长度)、当采样时刻t分别为0、2.5、5、7.5和10 ms、即0T、T/4、T/2、3T/4、T时刻(T为周期)、相移光栅的反射谱如图2所示。
图2 不同时间t下相移光纤光栅的反射谱
由图2可以看出、在不同采样时刻t下、相移光栅光谱形状呈周期性变化、光谱带宽展宽但随着t变化不明显、反射谱中透射窗口的通透率不变。前半周期内、透射窗口所对波长向短波长方向漂移、同时短波长方向谐振峰逐渐增多; 后半个周期变化规律与前半周期相同、且0T时刻与T时刻光谱形状完全一致。不同时刻t下的峰值反射率和透射窗口对应波长的变化关系如图3、在一个周期内当光谱形状对称时、峰值反射率最低、但整个周期内反射率变化很小。可以看出、通过跟踪相移光栅透射窗口的波长漂移、可获取不同时刻动态应变场的变化、从而监测声发射信号的时变特性。
图3 透射窗口所对波长与峰值反射率随t的变化
2.2 PS-FBG光谱对频率f的响应特性
考虑不同声发射频率对相移光栅光谱的影响、令幅值a=100 με、衰减系数b=1、λE=0.5L(L为栅区长度)、时间t为2.5 ms、当f分别为10、1 310、2 610、3 910与5 210 Hz时、PS-FBG反射光谱如图4所示。不同频率f下峰值反射率和透射窗口对应波长的变化关系如图5。
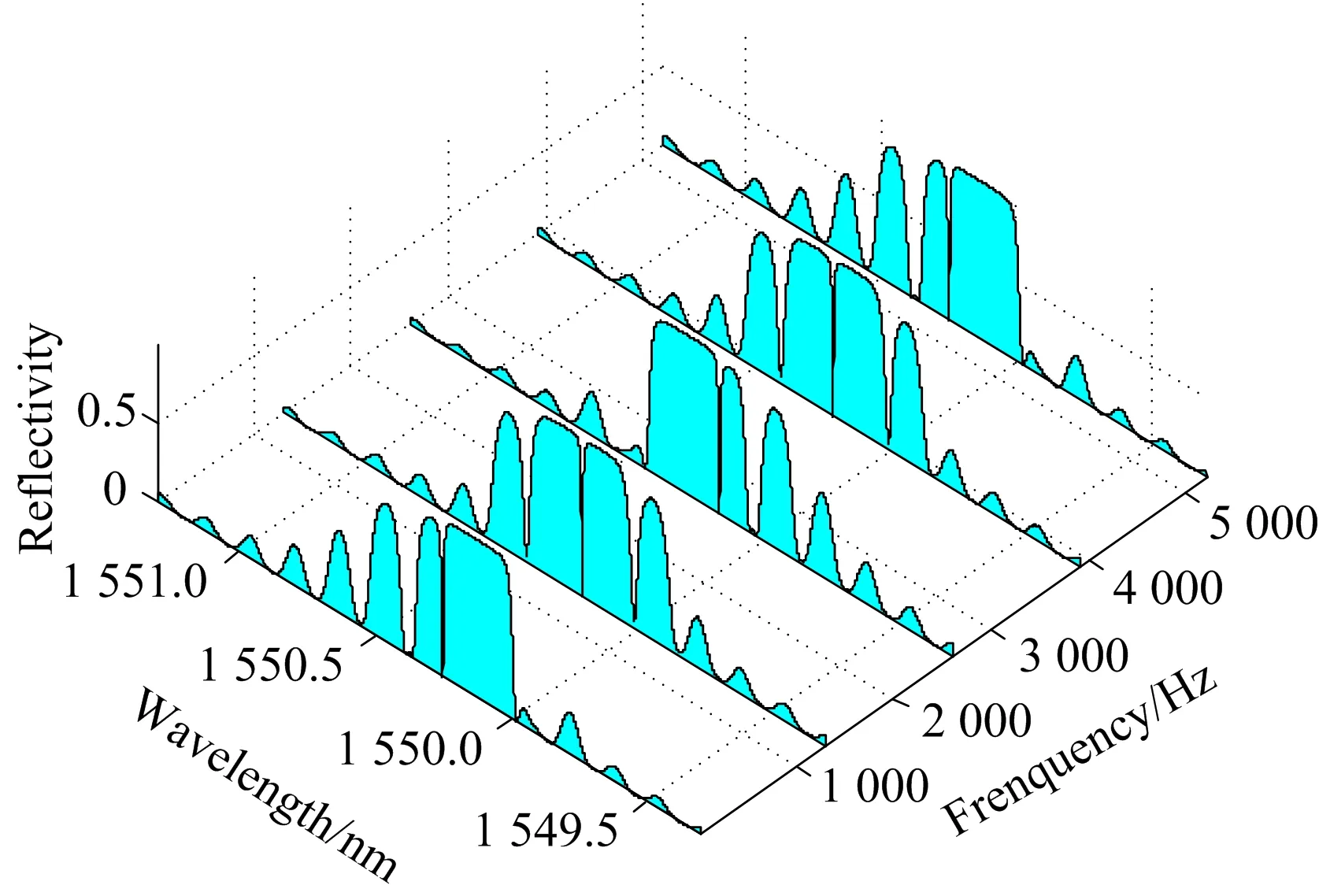
图4 不同频率f下相移光纤光栅反射谱
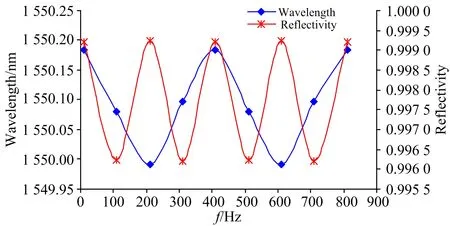
图5 透射窗口所对波长与峰值反射率随f的变化
可以看出、相移光栅光谱在动态应变作用下产生多个谐振峰、光谱带宽展宽、反射谱中透射窗口的通透率不变。不同频率f下、相移光栅透射窗口所对波长发生周期性漂移、且谐振峰位置随着透射窗口所对波长的漂移出现周期性移动。峰值反射率变化随频率呈现周期性变化。可以认为、当时间t、幅值a、衰减系数、及波长λE固定不变时、不同频率f的变化等效于对相移光栅相移量φ的调制。
2.3 PS-FBG光谱对幅值a的响应特性
令t=2.5 ms、f=100 Hz、衰减系数b=1、λE=0.5L、当幅值a分别为±400、±200与0 με时、仿真所得PS-FBG的光谱变化如图6。
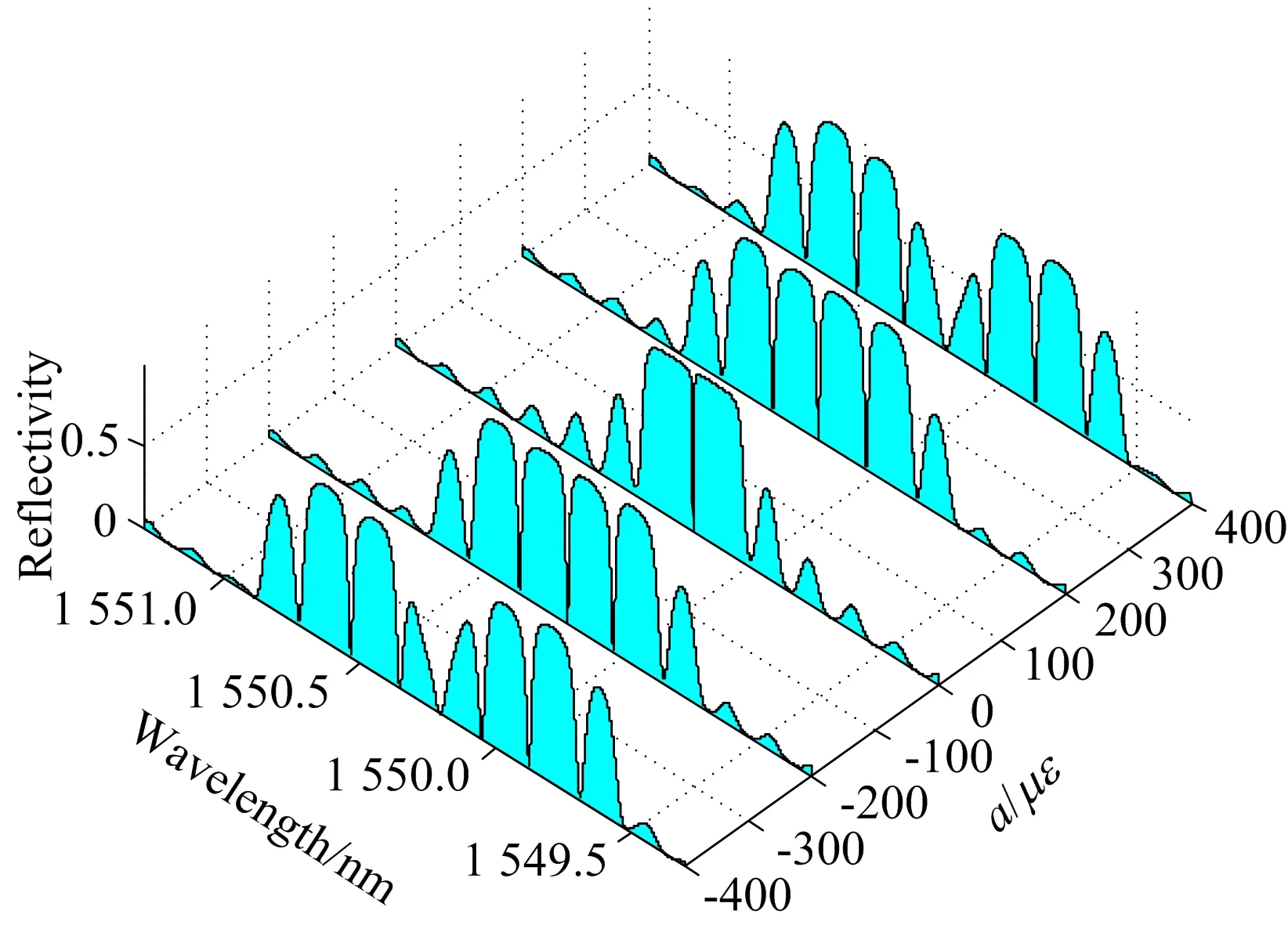
图6 不同幅值a下相移光纤光栅反射谱
如图6所示、随着幅值a的增大、相移光栅反射谱的谐振峰数量逐渐增多、并向分别向两侧延伸、透射窗口带宽展宽、说明空间周期性分布的动态应变场对相移光栅的作用效果逐渐增强。
在该仿真条件下、透射窗口所对波长及峰值反射率随a的变化关系如图7。可以看出、当a>0 με时、随着a的增大、相移光栅受拉应变作用增大、通透窗口所对波长向长波长方向漂移、然后逐渐减缓并最终到一恒定值、当a>300 με时、谐振峰数量增多、且光谱畸变严重; 当a<0 με时、栅区受压应变作用、随着a绝对值的增大、透射窗口所对波长向短波长方向漂移、且漂移量逐渐减缓并最终到一恒定值。整个过程中相移光栅光谱保持对称、且波长变化量很小、约为7 pm。当a=0 με时、峰值反射率最大、随着a绝对值的增加、反射率逐渐递减。因此、幅值a的变化主要影响谐振峰的数量、对透射窗口波长漂移影响不大。
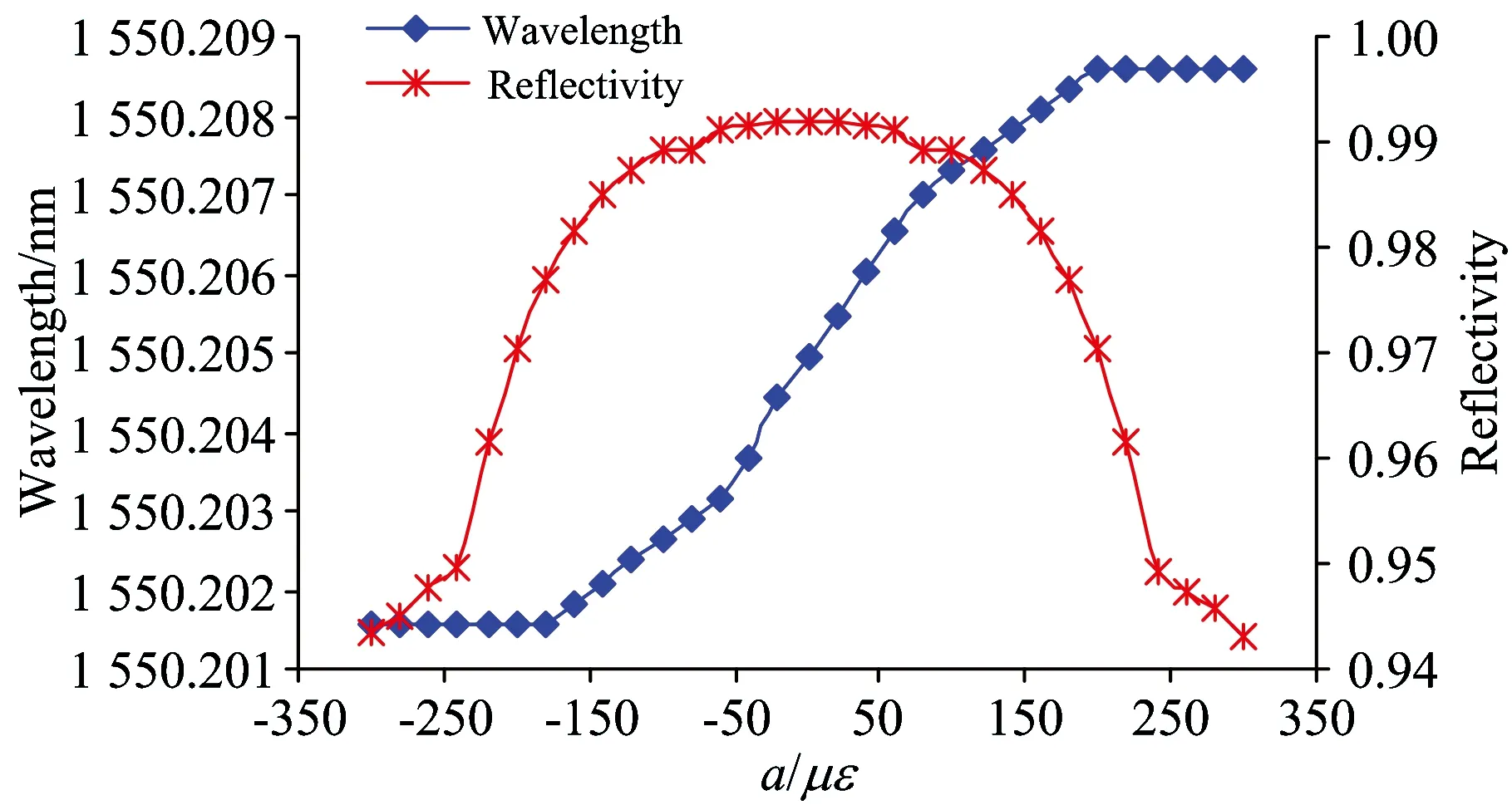
图7 透射窗口所对波长与峰值反射率随a的变化
2.4 PS-FBG光谱对衰减系数b的响应特性
令t=2.5 ms、f=100 Hz、幅值a=100 με、λE=0.5L、分析不同衰减系数b变化下、PS-FBG的光谱变化规律。当b分别为0.001、0.003、0.005、0.007与0.009时、反射谱如图8(a)所示、可以看出、当b较小时、相移光栅光谱不对称、长波长侧光谱形状基本不变、短波长侧产生大量旁瓣、随着b的增大、长波长侧逐渐形成谐振峰、短波长侧的旁瓣逐渐增多并逐渐形成谐振峰。这是由于b较小时、动态应变场在栅区范围内迅速衰减、此时周期性的应变场作用不明显、栅区受不均匀静态应变场作用、光谱局部发生展宽并产生旁瓣; 随着b的增大、周期性应变场作用加剧、表现为光谱谐振峰逐渐增多。
当b分别为0.01、0.05、0.1、0.15与0.2时、相移光栅反射谱如图8(b)所示、此时动态应变场在栅区范围内衰减梯度小、光谱在周期性应变场作用下光谱产生谐振峰并趋于对称、对着b进一步增大、光谱形状不再变化、此时的动态应变场在栅区范围内衰减梯度很小、对光谱影响可以忽略不计。
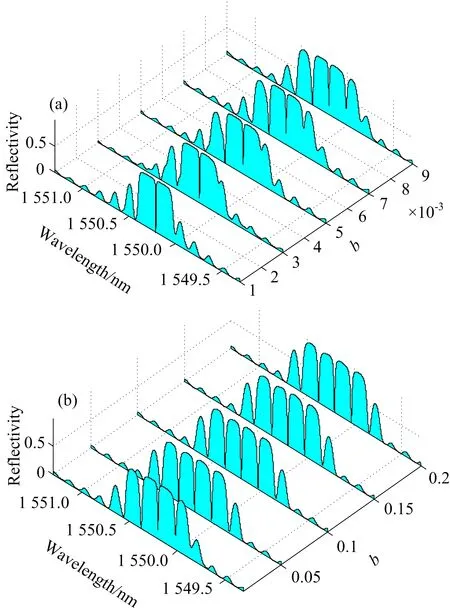
图8 不同衰减系数b下相移光纤光栅反射谱
在该仿真条件下、透射窗口所对波长及峰值反射率随b的变化关系如图9。可以看出、当b小于0.005时、透射窗口所对波长随着b的增加先向短波长方向漂移、b大于0.005时、波长迅速向长波长方向移动、b继续增大、波长逐渐趋于恒定值、说明此时动态应变场在栅区范围衰减梯度非常小。当b较小时、反射率有降低的趋势、但变化很小、随着b的增大、反射率迅速降低、当b为0.04时、反射率变化逐渐趋于平稳。
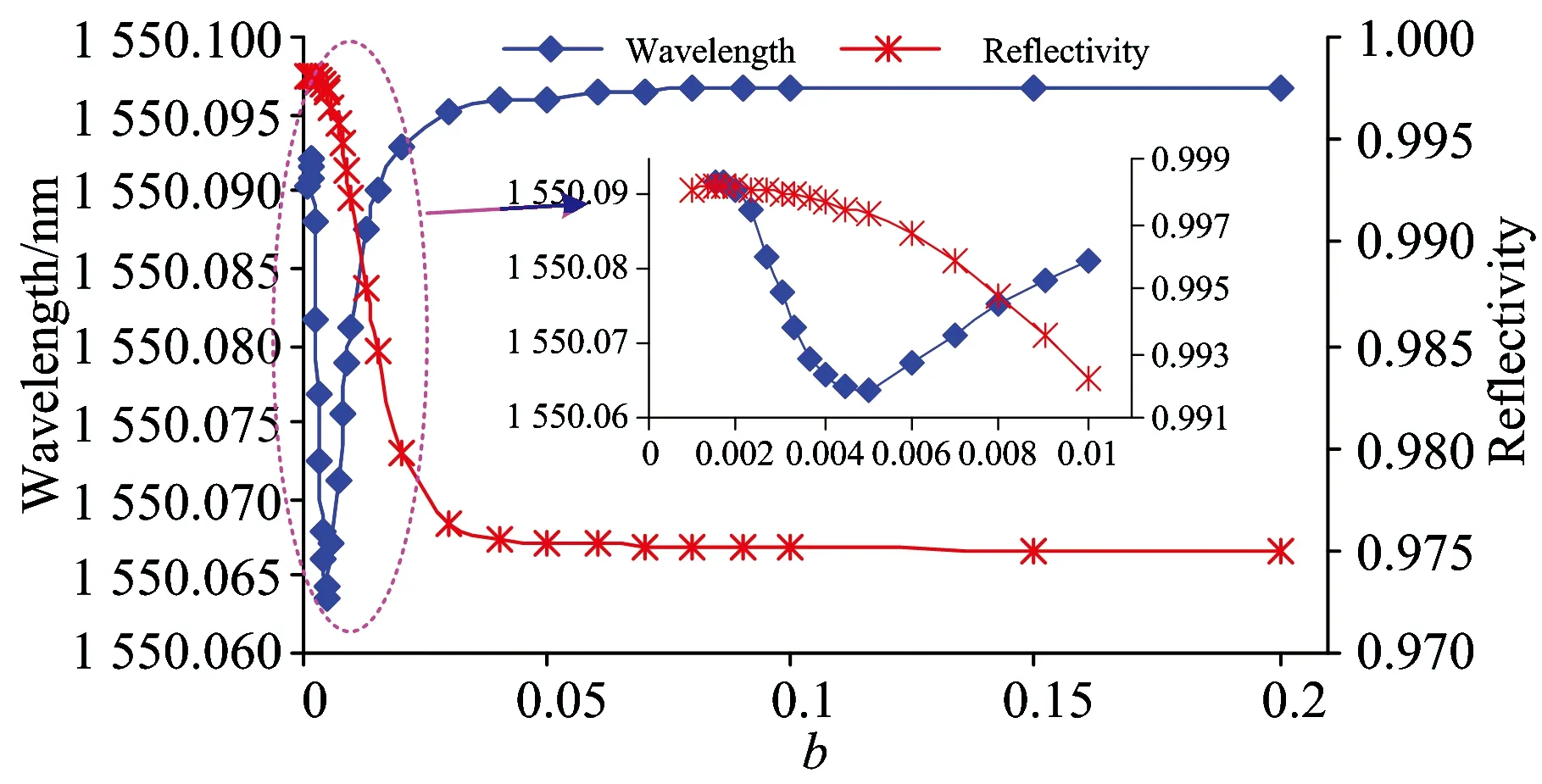
图9 透射窗口所对波长与峰值反射率随b的变化
2.5 PS-FBG光谱对波长λE的响应特性
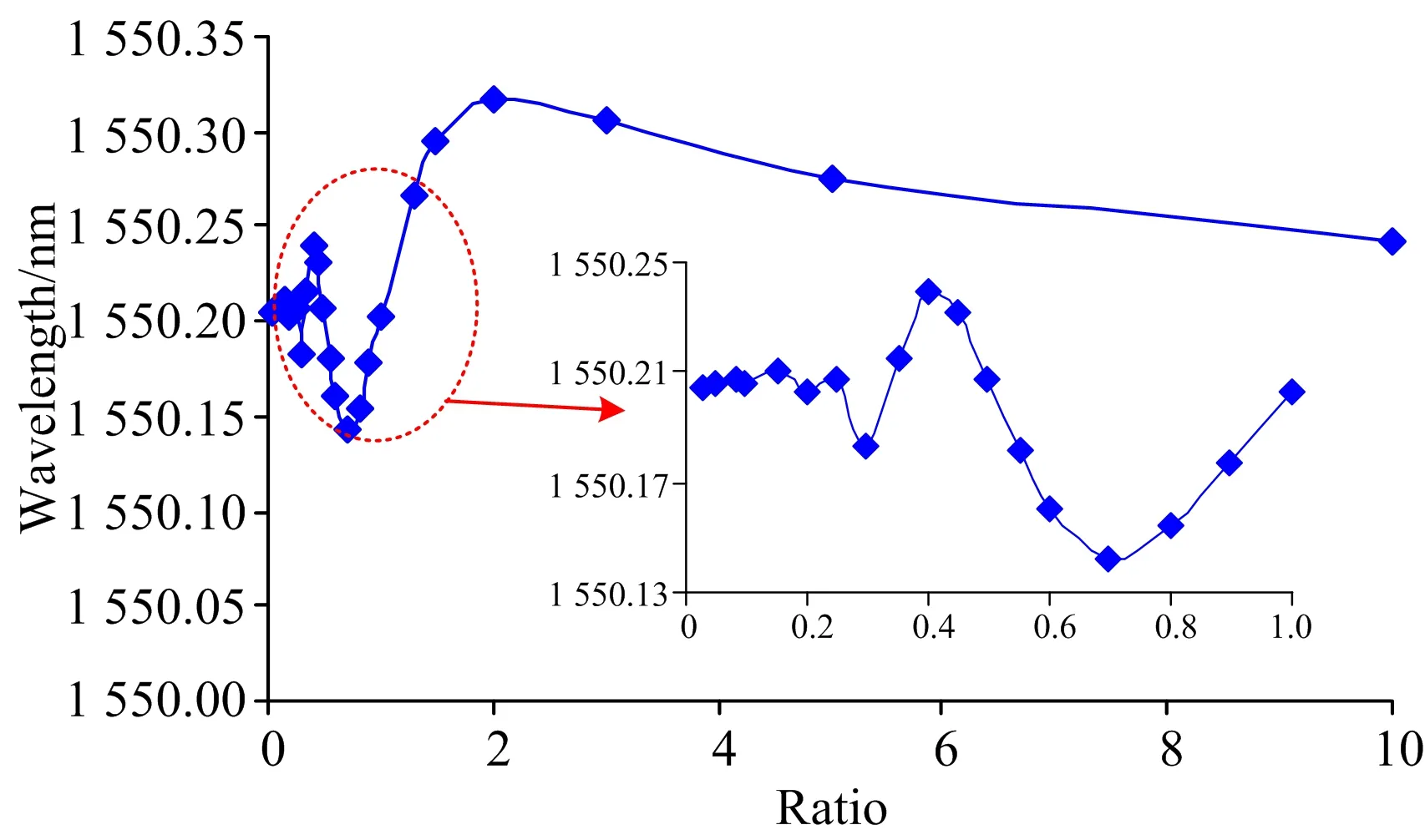
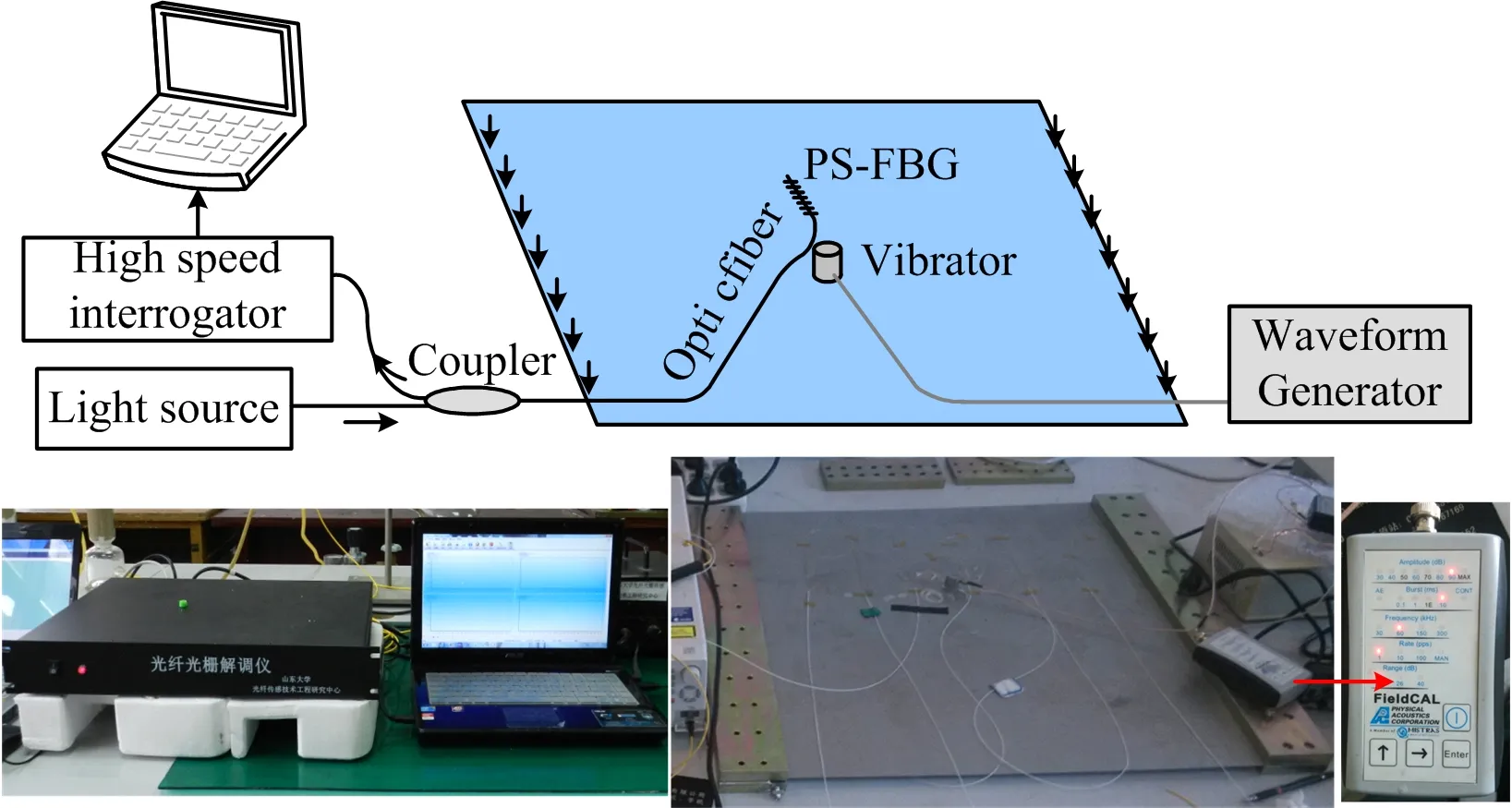
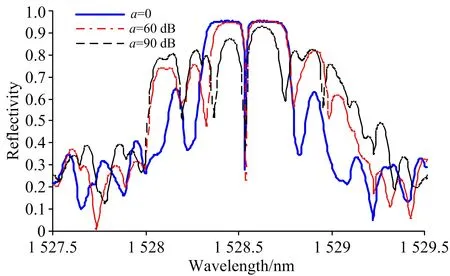
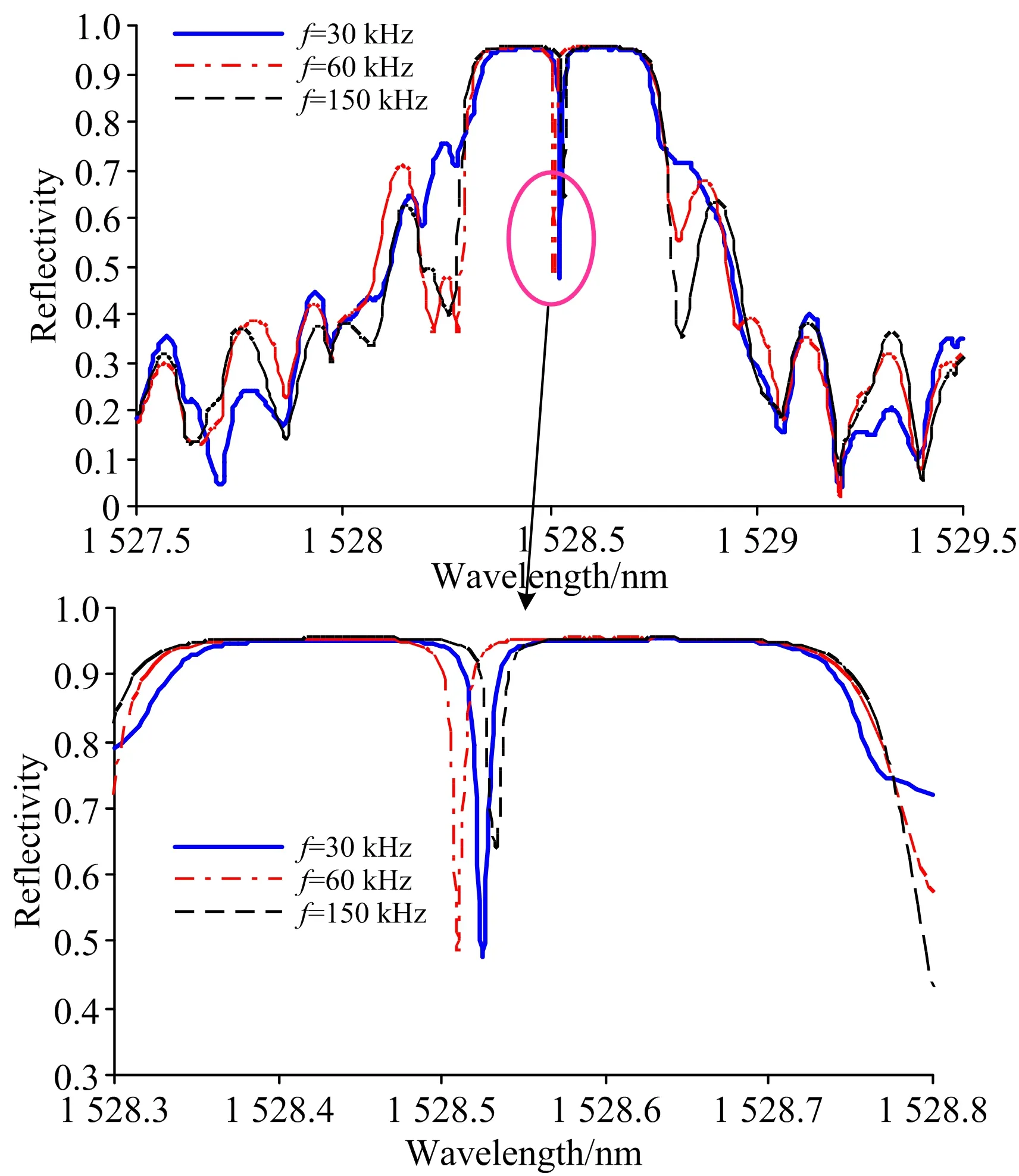
引入系数Ratio、且Ratio=λE/L、L为栅区长度。令t=2.5 ms、f=100 Hz、幅值a=100 με、衰减系数b=1、Ratio分别为0.05、0.1、0.3、0.5、0.8、1、2、3、5、10、分析这10种情况下PS-FBG的光谱响应特性、如图10。可以看出当Ratio<0.1时、即波长λE小于0.1L时、光谱形状基本不变、说明此时波长对光谱影响很小。当0.1 图10 不同声发射波长下相移光纤光栅反射谱 透射窗口所对波长随不同情况下Ratio的变化关系如图11。当Ratio小于0.1、波长基本不变; 随着Ratio增大、波长变化呈现振荡特性、且振荡幅度逐渐增大。当Ratio大于2时、波长变化逐渐减缓、此时波长随着Ratio增大逐渐减小、这是由于此时作用在栅区的应变场近似为静态不均匀应变场、且Ratio越大、分布在栅区的应变场梯度变化越小。 图11 透射窗口所对波长随Ratio的变化 开展动态应变场激励试验、研究PS-FBG在动态应变场下的光谱特性、并验证仿真分析结果。搭建的试验台如图12所示、采用双边夹持的铝薄板作为动态应变场的传输介质、信号源选用MISTRAS手持式AE信号发生器FieldCAL、信号源幅值与频率可调。信号源产生的信号通过PZT作用于薄板产生动态应变场、将实验选用的相移光纤光栅靠近PZT、均匀粘贴在薄板表面、信号源产生的动态应变场通过薄板传递至PS-FBG。实验采用的PS-FBG设计波长为1 528.535 nm、栅区长度15 mm、相移量为π、相移点位于栅区中心。选用基于BaySpec FBGA-IRS高频采集模块开发的高速光纤光栅解调仪实现动态光谱采集、该模块具有高速并行处理和连续光谱测量能力、响应频率为5 kHz、波长精度为±1 pm。由于实验只需采集某一时刻的光谱、不要求捕捉时变的动态信号、因此在连续动态信号激励下、可采用该模块采集快速变化的动态激励下固定时刻的光谱、并通过软件Sense2020将采集的光谱数据保存至计算机。信号源与数据采集模块采用同步时钟控制。 图12 试验系统 设定信号发射器输出频率为150 kHz、幅值分别为0、60和90 dB。t为1 s时、采集不同幅值下PS-FBG的反射谱、如图13。可以看出随着动态应变幅度a的增大、反射谱出现展宽、且谐振峰的数量增多、并向两侧逐渐延伸、峰值反射率降低、但通透窗口所对波长位置变化不明显、说明幅值的增大影响反射谱谐振峰的数量、但对波长漂移影响不大、与仿真结果吻合。 图13 不同幅值a下实验所得相移光纤光栅反射谱 图14 不同频率f下实验所得相移光纤光栅反射谱 设定信号发射器幅值为30 dB、输出频率f分别为30、60和150 kHz。t为1 s时、采集不同频率下PS-FBG的反射谱、如图14。可以看出、当f为60和150 kHz时、二者反射谱形状接近、但透射窗口所对的波长位置不同、说明不同频率f影响了透射窗口所对波长位置、与仿真所得结论吻合。当f为30 kHz时、反射光谱展宽、且光谱两侧的旁瓣增多。这是由于在波速不变的情况下、频率越大、波长越短、波长与栅区长度比Ratio越大。当f为30 kHz时、此时Ratio较大、作用在栅区的应变场近似为沿轴向分布的不均匀应变场、光谱出现展宽、且旁瓣增多、符合仿真分析。 基于传输矩阵法建立相移光纤光栅在声发射激励产生的动态应变场传感模型、对不同动态应变场下相移光纤光栅的光谱特性进行仿真、结果表明不同声发射激励信号的频率f与周期内不同采样时刻t会导致PS-FBG反射谱中透射窗口所对波长周期性漂移、其影响等效为对相移量φ的调制; 动态应变场的幅值a越大、PS-FBG反射谱的谐振峰数量越多、但对透射窗口所对波长位置影响不大; 当动态应变场在栅区范围内衰减梯度较大时、PS-FBG反射谱出现单边光谱展宽现象并出现旁瓣、随着衰减梯度的减小、展宽一侧逐渐形成谐振峰; 声发射信号的波长λE在0.1~2L范围内对PS-FBG光谱有较大影响、且透射窗口所对应波长漂移产生振荡特性、超出该范围、PS-FBG光谱变化不明显。搭建连续信号激励下的动态应变场实验平台、研究不同幅度a与频率f变化下PS-FBG的光谱特性、实验结果与仿真结果较好吻合。表明不同声发射激励产生的动态应变场下相移光纤光栅光谱不同、呈现一定规律性、本文为基于光纤光栅传感技术的声发射传感提供理论指导。 [1] Sengupta Sanjay,Datta Aloke Kumar,Topdar Pijush. Latin American Journal of Solids & Structures、2015,12(8): 1565. [2] Xu N W,Li T B,Dai F,et al. Engineering Geology,2015,188(2015): 48. [3] Masanori Takuma,Shigeyoshi Hisada,Kenichi Saitoh、et al. Advances in Materials Science & Engineering; 2014,(2014):274071-1-12. [4] NIE Fei、GAO Xin、GU Xian-ming,et al(聂 飞,高 昕,顾先明、等). Coal Engineering(煤炭工程),2015,47(4): 19. [5] PANG Dan-dan(庞丹丹). Ji’nan: Shandong University(济南: 山东大学)、2014. [6] Xia Mingjun,Jiang Mingshun,Sui Qingmei、et al. Optik、2015,126(11-12): 1150. [7] WANG Jing,JIANG Shan-chao,SHI Bin、et al(王 静,蒋善超,施 斌、等). Spectroscopy and Spectral Analysis(光谱学与光谱分析),2014,34(8): 2021. [8] Huang Wenzhu,Zhang Wentao,Zhen Tengkun,et al. Journal of Lightwave Technology. 2014,32(22): 4294. [9] CAI Lu-lu,WU Fei,WANG Yu-tian(蔡璐璐,吴 飞,王玉田). Chinese Journal of Laser(中国激光)、2009,36(8): 2070. [10] JIANG De-sheng,LIAO Sheng-hui,ZHOU Ci-ming、et al(姜德生,廖胜辉,周次明、等). Acta Photonica Sinica(光子学报)、2005,34(10): 1577. [11] YU Qian,SHEN Chang-yu(虞 倩,沈常宇). Journal of China University of Metrology(中国计量学院学报)、2009,12(4): 324. [12] JIANG Meng,ZHANG Wei-gang、JIN Long、et al(姜 萌,张伟刚,金 龙、等). Chinese Journal of Laser(中国激光)、2009,36(4): 873. [13] LU Shao-hua,XU Ou,FENG Su-chun、et al(鲁韶华,许 鸥,冯素春、等). Acta Optica Sinica(光学学报)、2008,28(9): 1675. [14] YU Hua-qing(余华清). Chinese Journal of Sensors and Actuators(传感技术学报)、2006,19(3): 814. [15] Qi Wu,Yoji Okabe,Kazuya Saito,et al. Sensors、2014,14(1): 1094. *Corresponding author Research on the Phase-Shifted Fiber Bragg Grating Spectra under Dynamic Strain Fields WANG Zheng-fang1,2,WANG Jing1,SUI Qing-mei1* 1. College of Control Science and Engineering,Shandong University,Ji’nan 250061,China 2. Nanyang Technological University Energy Research Institute@NTU,Singapore 639798 Fiber optic sensing technology has been widely used for acoustic emission (AE) measurement in aerospace and geotechnical engineering due to the advantages of immunity to electro-magnetic interference,high accuracy,and multiplexing capacity. As for the fiber Bragg grating based on AE measurement system,traditional efforts have been made to study the spectra of Fiber Bragg Grating under AE signal. While this paper focused on phase-shifted fiber Bragg grating (PS-FBG) which is a new type fiber Bragg grating,and investigated the spectra of under dynamic strain field generating with an AE signal. A dynamic strain sensing model of PS-FBG was built based on the transfer matrix theory,and a cosine exponential attenuation function was utilized to simulate the dynamic strain field. Then the effects of amplitude,sampling time,exponential attenuation coefficient,frequency and wavelength of AE signal on the spectra of PS-FBG were studied in detail using numerical simulation. The result demonstrate that the spectra of PS-FBG changes periodically with frequency and different sampling time,especially the peak wavelength of the transmission window in the PS-FBG spectrum shifts periodically; and the increase of amplitude mainly contribute to more harmonic peaks in the reflected spectrum. The attenuation coefficient affects the spectrum of PS-FBG within certain range. And the AE wavelength affect the spectrum of PS-FBG when it is between 0.1 to 2 L,beyond the range,the spectrum of PS-FBG has minor variation with the AE wavelength. Finally,dynamic strain experiments were conducted,and the spectrum of PS-FBG under continuously vibration signal with different amplitude and frequency were logged for analysis. The experimental results agree well with simulation,which indicate that under different dynamic strain fields generated by AE signal,the spectra of PS-FBG are different,while the variation of spectra follows certain laws. This paper provides theoretical support for the AE measurement system on the basis of PS-FBG. Phase-shifted fiber Bragg grating; Dynamic strain fields; Acoustic emission (AE) measurement Dec. 22,2015; accepted Apr. 20,2016) 2015-12-22、 2016-04-20 国家自然科学基金面上项目(41472260)、国家高技术研究发展计划(863计划)(2014AA110401)资助 王正方、1988年生、山东大学控制科学与工程学院博士后 e-mail: wangzhengfangsdu@foxmail.com *通讯联系人 e-mail: qmsui@sdu.edu.cn TN253 A 10.3964/j.issn.1000-0593(2016)12-4113-07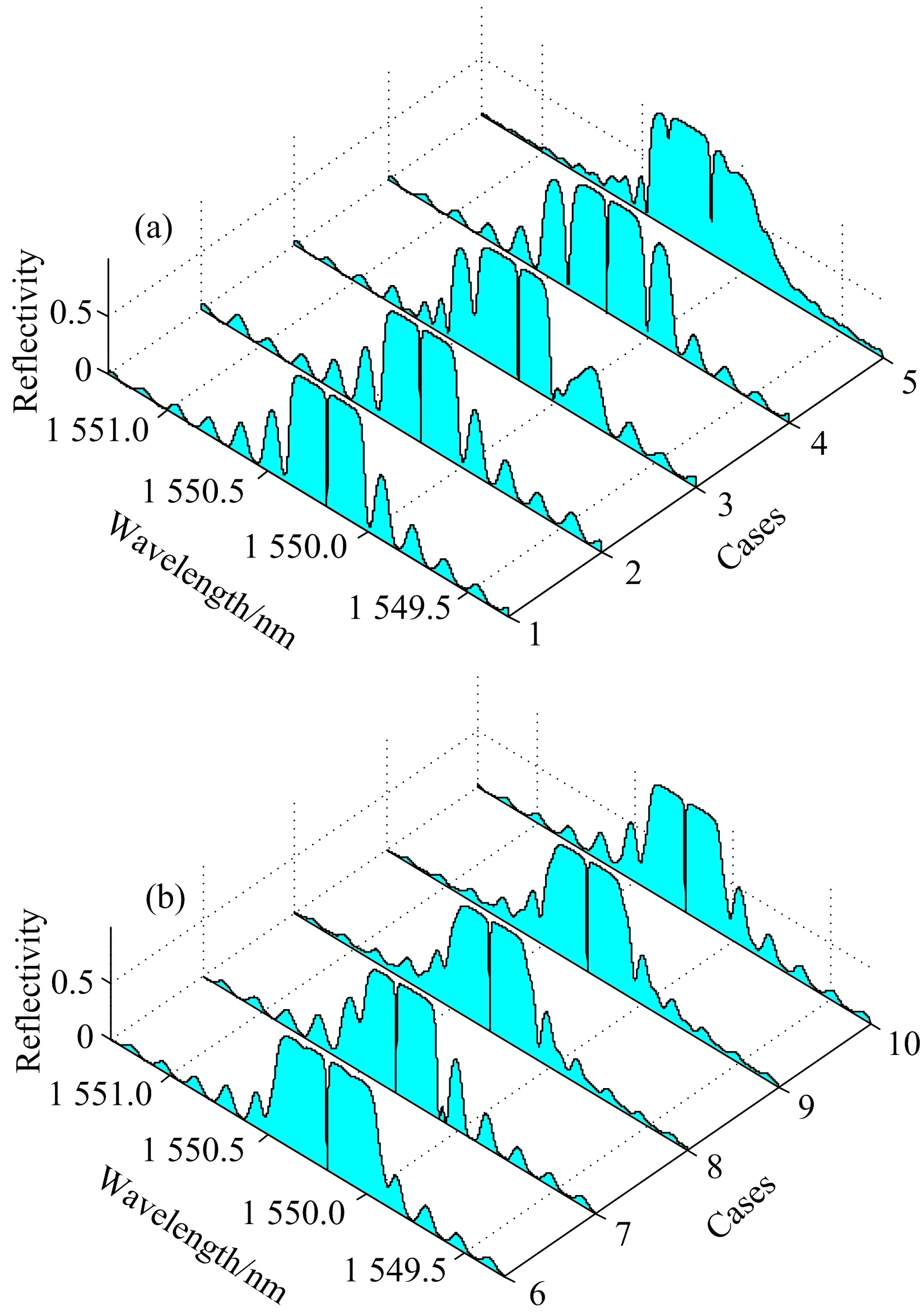
3 相移光纤光栅光谱动态应变试验
4 结 论
猜你喜欢
杂志排行
光谱学与光谱分析的其它文章
- Studies on the Interaction of Perfluorononanoic Acid with Human Serum Albumin by Multi-Spectroscopic,Molecular Docking and Isothermal Titration Calorimetry Techniques
- Study on Emission Spectrum of OH Radicals in a Combination System of Pulsed Discharge Plasma and Activated Carbon
- Simulating the Three-Dimensional Image of Cold Atomic Cloud
- K Shell Fluorescence Parameters by Impact of 5.96 keV Photons on Ti and Its Compounds
- Structure Effect on K Shell Fluorescence Parameters at Bis-4-Bromobenzyl-1,2,4-Triazol-3-Ones
- 基于Wollaston棱镜的图像复分快照式成像光谱仪设计
