基于贝叶斯模式平均与标准化异常度的东江汛期降水预报*

吴裕珍，冯志州，王大刚

(中山大学水资源与环境系，广东 广州510275)

基于贝叶斯模式平均与标准化异常度的东江汛期降水预报*

吴裕珍，冯志州，王大刚

(中山大学水资源与环境系，广东 广州510275)

考察贝叶斯模式平均(BMA)对第二代气候预报系统(CFSv2)在东江流域汛期月降雨量预报的订正效果，同时引入标准化异常度(SA)指标识别异常的降雨值，分别进行SA的确定性预报以及集合预报，通过建立SA和BMA结果之间的联系构建一个较为完整且精度较好的降雨预报模型，提高东江流域中长期降雨预报的精度。主要结论如下：①BMA50%以下的分位数不具有预报作用，75%分位数具有最优的预报效果。但BMA还存在不足之处，常表现为对极端降雨的低估；②利用CFSv2集合平均值进行SA计算时，SA严重偏小，可能说明CFSv2存在系统性误差。对CFSv2原始预报分别进行伽玛函数订正以及多项式订正后，降水预报成功指数(Ts)和异常值报对的次数有明显地提高，但预报偏差(Bs)也相应地增大；③ SA与BMA之间大致可建立如下的关系，即当SA判断会出现异常值时可选择95%分位数的预报值，相反则选择75%分位数预报值。

BMA；SA；CFSv2；汛期；东江流域

中长期降雨预报是水资源管理、水安全、旱涝灾害预警预防以及粮食安全等的基础[1-3]，同时作为气候、水文模型不可或缺的驱动因子之一对研究中长期的气候变化、水文过程等也十分重要[4-5]。

因此一些业务气候预报中心相继研发了气候预测模型并不断更新模型的版本[ 6-8]，在这些气候预测模型中，由NCEP研发的第二代气候预报系统(Climate Forecast System version2, CFSv2)研究、应用得较为广泛，在季节气候预报中占有重要的地位，因此在不同的时空尺度上开展评估CFS预报能力的研究[9-12]，如Luo等[13]评估了CFSv2对中国夏季温度和降雨的预报表现，研究认为相比温度的预报效果而言，对降雨的预报效果要更差，而且再预报数据对中国东部的降雨存在干偏差。由这些研究评估可知，尽管CFS在不断完善，但是其对季节降雨的预报还存在较大的误差，而且预报效果不稳定，随着时空尺度的变化而呈现无明显规律的变化，因此可能需要针对特定的时空尺度对CFS原始的预报值进行后处理，即误差订正。

本文将考察的是近年来被新引进气象气候领域的一种后处理方法——贝叶斯模式平均(Bayesian Model Averaging, BMA)对CFS预报误差的订正效果。经Raftery等[14]和Sloughter等[15]发展和改进后，BMA被广泛应用于短期温度、降雨等天气要素的概率预报中且均在不同程度上降低了天气要素的预报误差[16-17]，而对于BMA对季节降雨预报的误差订正，Peng等[18-19]利用BMA分别对PREC/L(the Precipitation REConstruction over Land)、ECMWF System4 outputs在中国的季节性降雨预报误差进行订正，认为订正的效果在预见期为1个月时有较明显地改善。

虽然BMA能够提供不同降雨值出现的概率，但对决策者而言，选择分位数时往往只能根据经验或预报值的用途，缺少选择时可供参考的客观信息，因此本文还将引入标准化异常度 (Standardized Anomaly, SA)指标识别异常的降雨值，SA常被用于异常值的识别，如HPC (the National Centers for Environmental Prediction’s Hydrometeorological Prediction Center)将SA用于评估数值天气预报模型的预报能力，杜钧等[20]分析了SA对罕见极端高影响天气预报的可靠性，指出SA识别出了大暴雨事件，而且还有助于认识异常天气发生的原因。除一般的采用确定性预报进行SA的判别外，本文将进一步基于集合预报的概念尝试获得预报的可信度信息，即SA集合异常预报，并尝试建立SA和BMA结果之间的联系。

东江承担供水、防洪、发电、通航等多种任务，因此对该流域而言，汛期降雨预报的精度将极大地影响到汛期水量调度、洪水的预警预报以及水资源管理等计划的制定，汛期的降雨预报十分重要。因此，本文将考察BMA对CFSv2在东江流域汛期月降雨量预报的订正效果，同时引入SA指标定性识别异常的降雨值，分别进行SA的确定性预报以及集合预报，最后尝试建立SA和BMA结果之间的联系，希望能建立一个较为完整且精度较好的降雨预报模型，提高东江流域中长期降雨预报的精度，减小误差。这不仅为更科学地制定流域水资源管理政策、水量调度计划以及洪水预警预报方案等提供参考，也为中长期降雨预报研究提供新的思路。

1 数 据

东江流域位于珠江流域东部，是珠江流域的一级支流，干流全长562 km，平均坡降0.35‰，总落差约440 m，流域总面积35 340 km2，其中广东省境内占流域总面积的90%，主要支流有西枝江、新丰江、秋香江等。东江属亚热带季风气候，平均年降水量为1 500～2 400 mm，时空分布不均匀，汛期(4-9月)的降水量占全年降水量的80%以上，而在空间上，一般是西南部降水较多，东北部较少。

本文的实测降雨数据来自于东江流域73个雨量站自1982-2009年日降雨量(图1)，经累加后得到月降雨量，经计算对比发现(图2)，在东江流域算术平均法和泰森多边形法计算得到的面降雨量十分接近，可以说这两种方法都适用于东江流域的面雨量计算，在此种情况下，较简便的方法或许是更优的，因此我们选择使用简便的算术平均法计算面雨量。

CFSv2在2011年3月30日正式投入业务运行，提供实时的季节预报[9]。CFS系列通过模拟大气、海洋和陆地的耦合作用来预报中长期气候状况，属于海-陆-气耦合的动力季节预报系统，相比CFSv1，CFSv2融合了一些新的物理包，包括陆面、海洋和海冰过程，具有新的大气—海洋—陆地数据同化系统，以及具有更高的空间分辨率(T126)[21]。CFSv2提供了1982-2009年28 a的回溯性预报数据，每5 d预报一次，1 d内有4个循环(00、06、12、18 UTC)[22-23]。本文的预报值采用CFSv2的再预报数据每年3月2、7、12、17、22和27日的所有预报未来9个月每6 h的降雨强度，一共有24(6×4)个成员。由于CFSv2预报范围基本覆盖全球(纬度范围89.28°N-89.28°S以及经度范围0°～359.06°)，因此本文截取东江流域所在的格网(纬度为21.26°N-25.04°N和经度为112.50°E-116.25°E)，利用ARCGIS等软件计算各个网格(共10个)占流域的面积，并以此为权重计算东江流域的面降雨预报值。

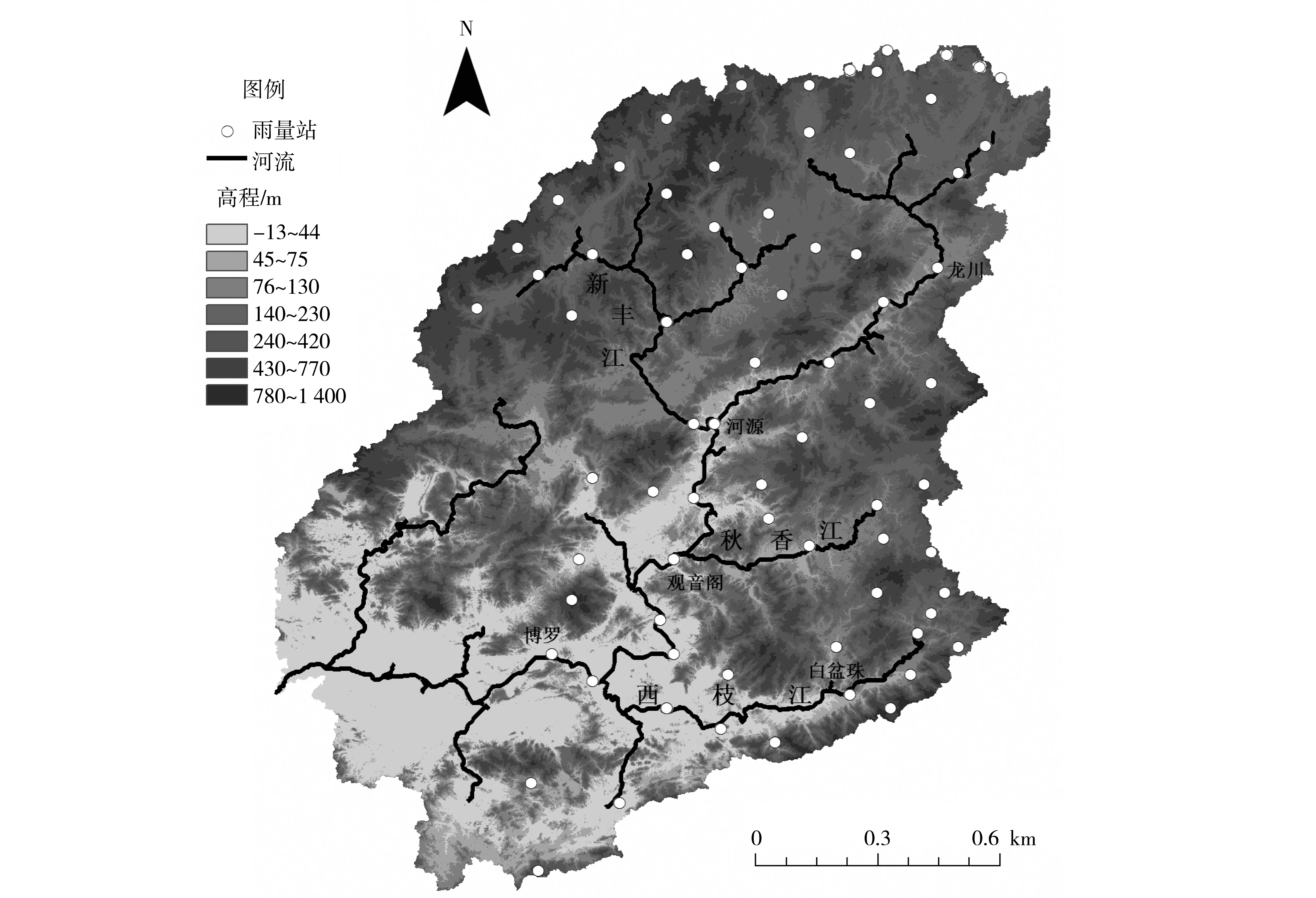
图1 东江流域及雨量站分布Fig.1 Location of rain-gauge in Dongjiang basin

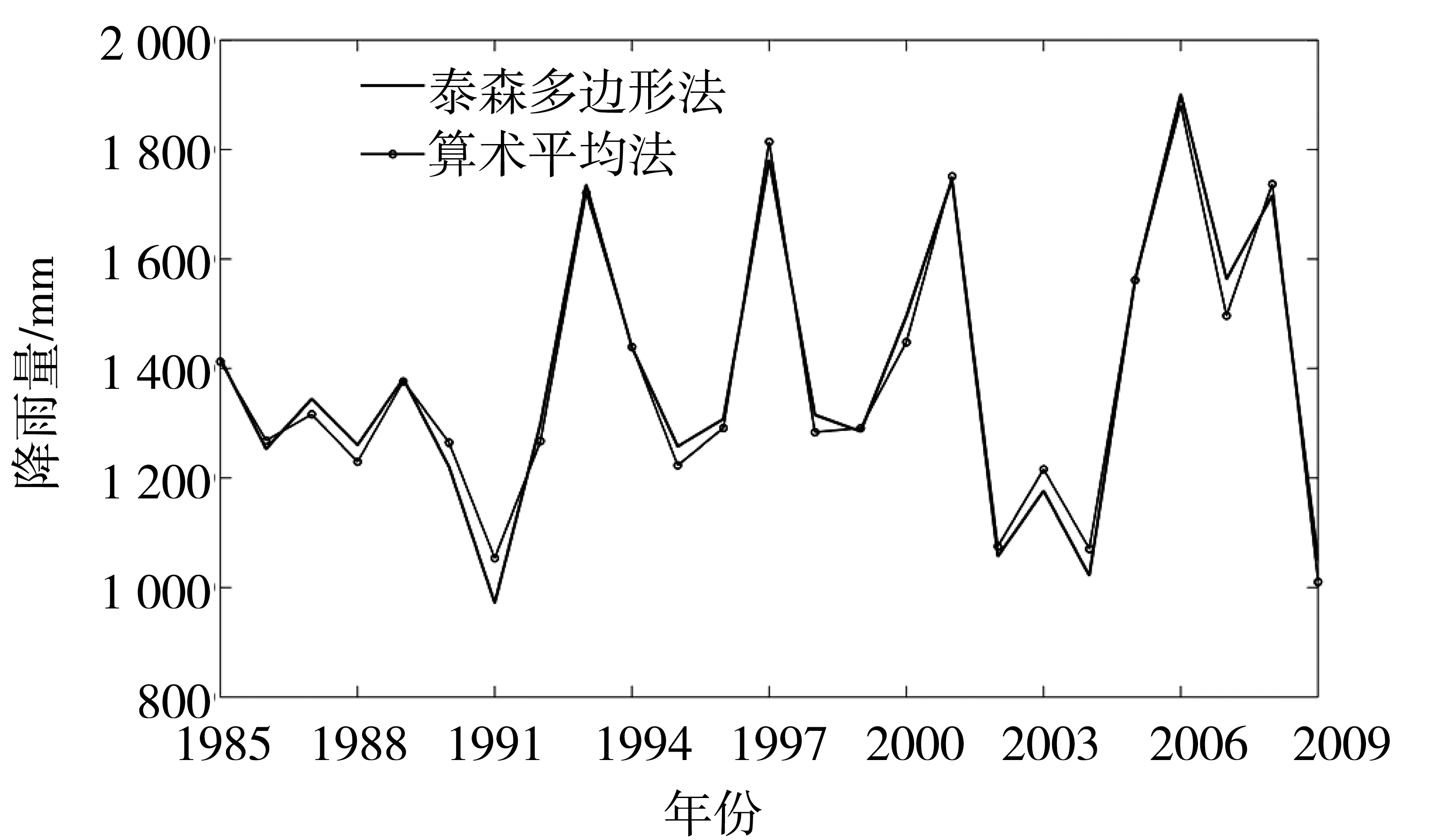
图2 泰森多边形法与算术平均法计算东江面降雨量比较Fig.2 Precipitation of Dongjiang basin calculated by Thiessen polygon and arithmetic mean

2 方 法

2.1 BMA

BMA是一种基于贝叶斯原理的数据后处理方法，被用于对多模型的预报和推理进行综合[24]，并得到相应预报量的概率密度函数。对全概率公式进行扩展可得到BMA预测模型[25]：

(1)

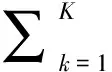
根据Sloughter等[26]的研究可以得到降雨量的BMA模型，其中用逻辑回归模型描述降雨量为0时的发生概率而用伽玛分布拟合非零时的降雨量分布[27]，其中逻辑回归模型为：

(2)

式中，a0,a1,a2为模型参数；φk为指示函数，当fk=0时，φk=1，否则为0；fk取立方根是因为这样可以在一定程度上修正其偏态性，从而取得较好的预报效果。

最终可获得降雨量的BMA模型：

(3)

2.2 SA

异常天气是以偏离当时、当地的气候平均值一定程度来定义的，因此可将一种天气要素的异常程度定义为它同实际气候平均值的差值。为便于天气要素在不同时空尺度下仍能进行比较，可将这一差值用该量的实际气候标准差进行标准化[20]，同时根据实际情况设置异常度阈值。本文经过试验设定异常度阈值为1，根据SA的原理计算平均值和标准差时应是固定窗口的滑动平均，经试验本文设定的窗口长度为21，并且定义月降雨量的异常值为≥90%百分位的实测值，当出现异常值时即为出现异常事件，SA的公式为：

(4)

式中，x和t分别表示地点、时间，F表示预报值，MEAN_O表示实测值的平均值，SD_O表示实测值的标准差。

由于由CFSv2集合平均值计算得到的SA值严重偏小，在异常事件出现时小于判别阈值，因此无法识别出异常事件，本文采用伽玛函数和多项式等方法对CFSv2预报值进行订正。首先分别计算实测值和预报值的经验频率，对伽玛函数订正方法来说，将预报值的经验频率代入由实测值拟合得到的伽玛函数的反函数中，得到订正后的预报值，对多项式订正方法而言，采用2阶多项式拟合实测值和其经验频率，再将预报值的频率代入得到订正后的预报值。这两种方法的实质都是频率匹配法。

2.3 评价指标

为评价不同时间尺度的预报值的预报效果，需选择归一化的评价指标。MAPE(MeanAbsolutePercentageError)是被广泛用于测量预报精度的评价指标，尤其适合于评价非负值的预报精度[28]，并被许多学者推荐使用，但由于MAPE在评价时对不同程度的偏差中赋予的是线性权重，无法突出大的偏差[29]，因此本文除MAPE外还有NRMSE(NormalizedRootMeanSquareError)，两个评价指标都是负导向的，即越小越好，公式如下：

(5)

(6)

(7)

式中，Pm-i和Po-i分别为第i个预报值、实测值。

而对于SA则采用预报常用的降水预报成功指数(Threat Score, Ts) 和预报偏差 (Bias Score, Bs)这两个评分参数，其中Ts越大表示预报效果越好，Bs越接近1预报效果越好。公式为

(8)

(9)

式中，NA为异常值预报正确的次数，NB为空报的次数，NC为漏报的次数。

3 结果与讨论

3.1 BMA对汛期月降雨量的预报

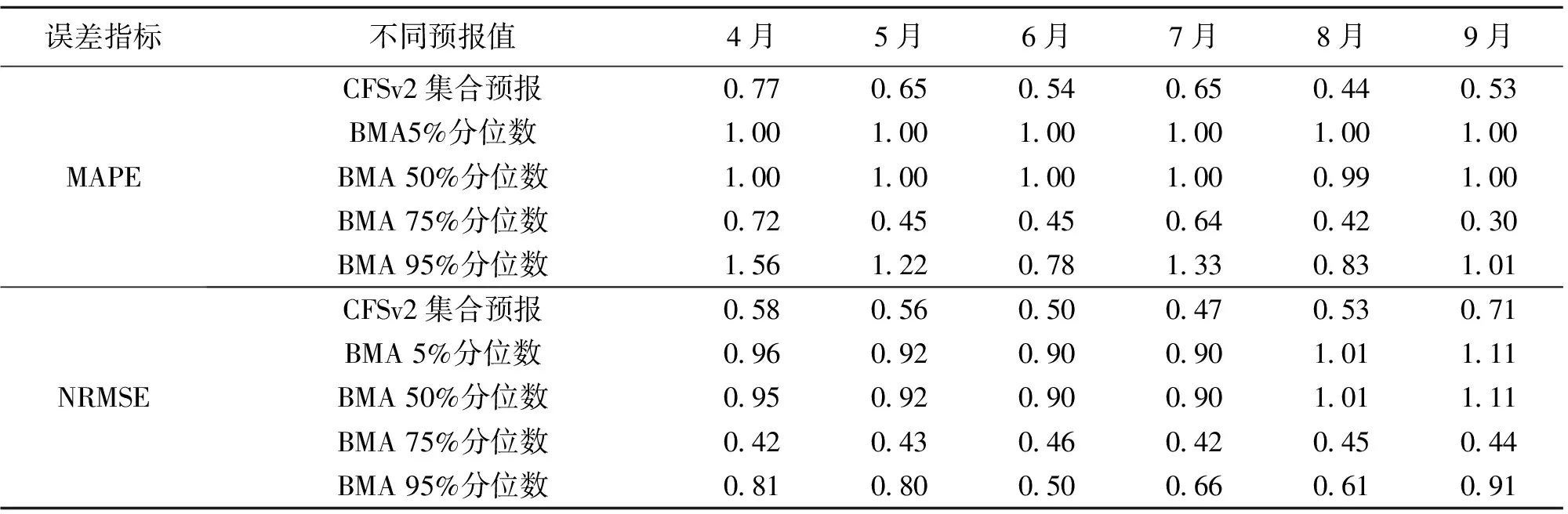
对BMA方法而言(图3和表1)，由于50%以下的分位数基本为0，没有有效的降雨信息，因此50%以下的分位数不具有预报作用，75%和95%分位数在不同程度上降低了原始预报的误差，其中75%分位数具有最优的预报效果，无论哪个月份、MAPE还是NRMSE，75%分位数的误差都是最小的，而且对5、9月的效果最明显，与CFSv2 集合预报(每个子集合误差的平均值)误差相比，误差减少了23%以上(5月MAPE、NRMSE减少率分别是31%、23%，9月为43%、38%)，从表1来看，BMA的预报能力受到原始集合的影响，尤其是MAPE，基本随集合预报误差先减小后增大的变化而出现相应的变化特征。图2也大致反应出相同的规律，4-6以及9月仅有2个月降雨未能预测到，应该注意的是，BMA有时也会出现误报的情况，如2009年6月的实测月降雨为734mm，但BMA却出现严重地低估(95%分位数的预报值也只有325mm)，对极端降雨的预报BMA还存在不足，常表现为低估，原因可能涉及BMA方法本身、求解的方法、参数率定及率定期的选择等多方面，需要进一步研究，实际上，目前存在的预报模式、预报方法都对极端降雨的预报有不同程度地缺陷，有待进一步完善理论和改进方法。但对于一般的降雨，BMA预报精度(75%分位数)还是很高的。因此，对非极端降雨进行预报时可以取75%分位数，而对于极端降雨则要采取较保守的策略用95%或以上的分位数作参考，当BMA预报的95% 分位数已超过警戒的雨量时，应做好相关的预警和预防工作，但该方法也会出现误报的情况，需要进行权衡和风险的评估。

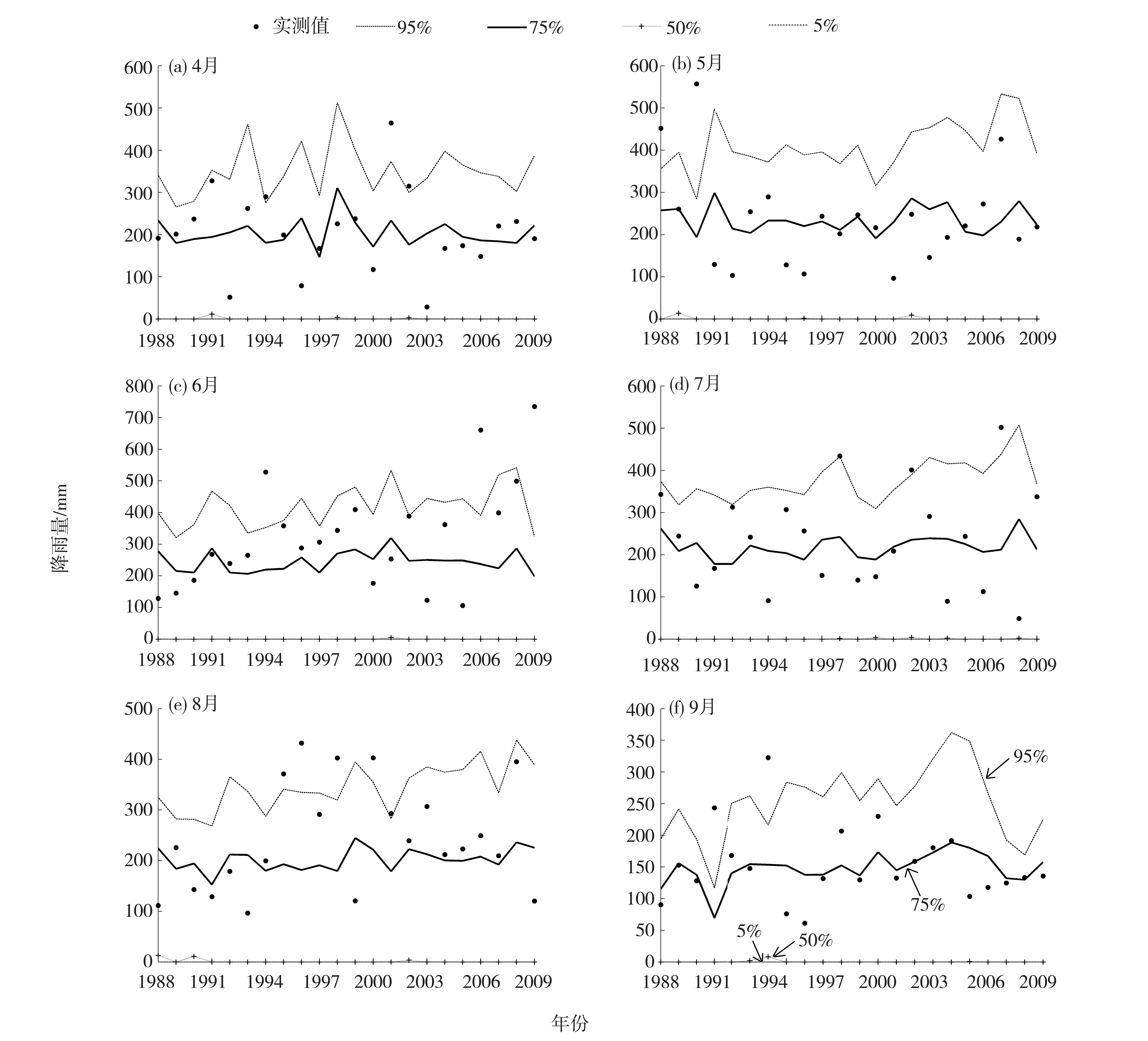
图3 东江汛期各月BMA不同分位数的降雨值Fig.3 Precipitation of different quantile of BMA in each month of flood season over Dongjiang basin

表1 东江汛期(4-9月)CFSv2集合预报值及BMA不同分位数预报的误差

Table1ErrorofCFSv2ensembleforecastinganddifferentquantileforecastingofBMAineachmonthoffloodseasonoverDongjiangbasin

误差指标不同预报值4月5月6月7月8月9月MAPECFSv2集合预报0 770 650 540 650 440 53BMA5%分位数1 001 001 001 001 001 00BMA50%分位数1 001 001 001 000 991 00BMA75%分位数0 720 450 450 640 420 30BMA95%分位数1 561 220 781 330 831 01NRMSECFSv2集合预报0 580 560 500 470 530 71BMA5%分位数0 960 920 900 901 011 11BMA50%分位数0 950 920 900 901 011 11BMA75%分位数0 420 430 460 420 450 44BMA95%分位数0 810 800 500 660 610 91

3.2 SA对汛期异常月降雨量的预报效果

从图4可知，利用CFSv2集合平均值进行SA计算时，CFSv2原始预报值严重偏小，相应的SA值偏小，在一共17次异常事件中，由CFSv2计算得到的SA仅有2次达到判别的阈值，即基于CFSv2的SA仅能识别出2次异常事件(表2)，Ts较小(0.08)，显著低估了异常度，杜钧等[30]指出，如果预报有很强的系统性偏差，结果可能会具有或高估或低估异常度的倾向，需要对原始的预报资料进行偏差订正。

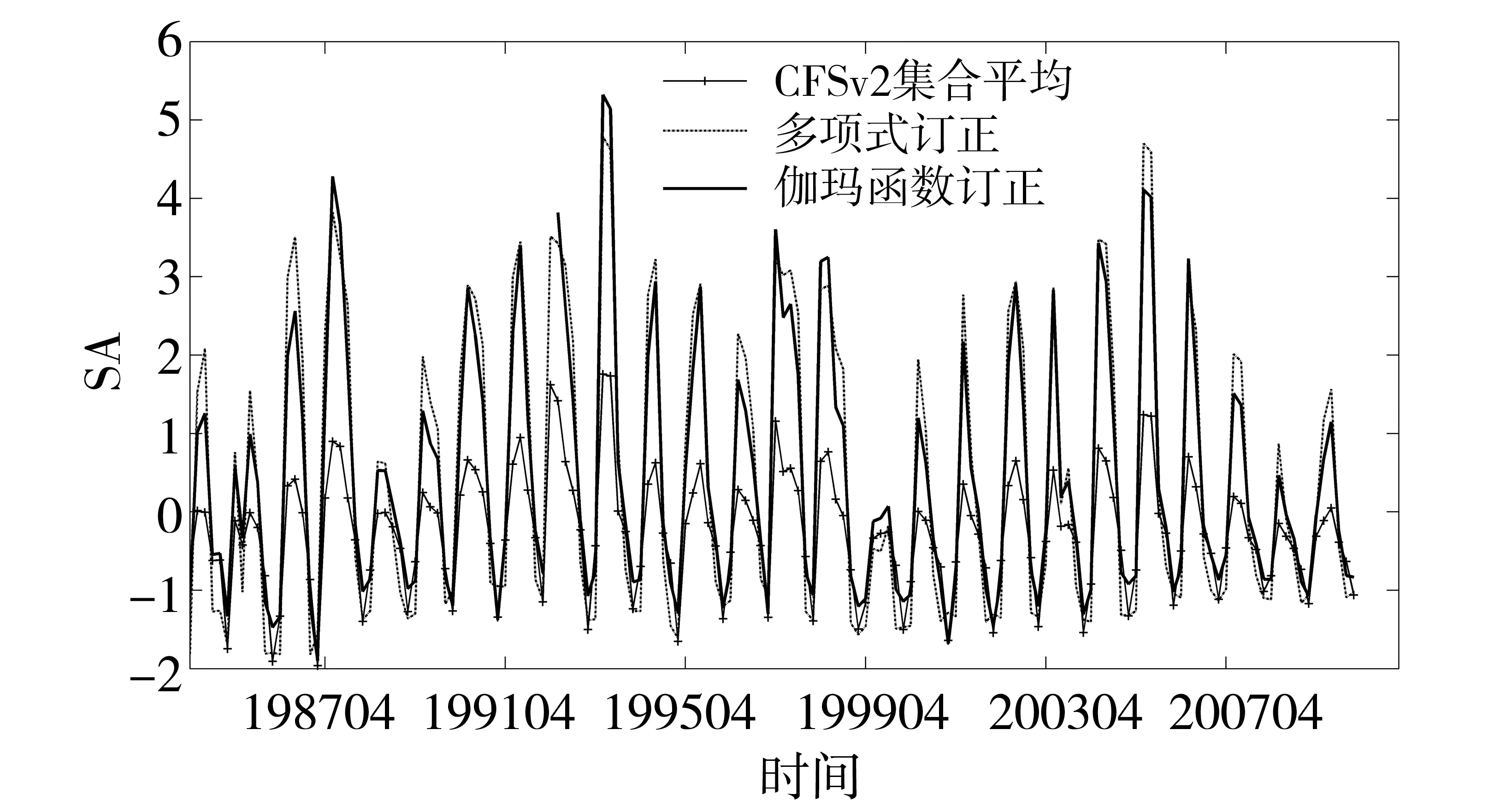
图4 CFSv2集合平均及校正后的SA情况Fig.4 SA of CFSv2 ensemble average and corrected values

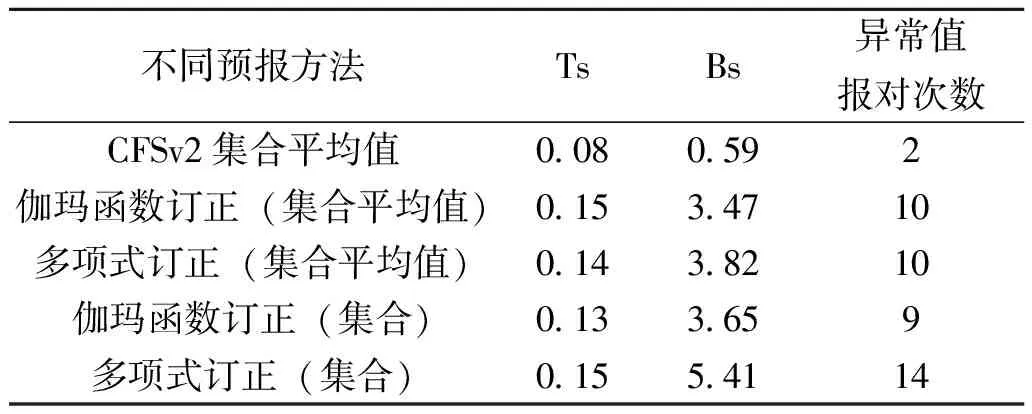
表2SA预报东江极端降雨误差情况

Table2ErrorofSAinforecastingextremeprecipitationsoverDongjiangbasin

不同预报方法TsBs异常值报对次数CFSv2集合平均值0 080 592伽玛函数订正(集合平均值)0 153 4710多项式订正(集合平均值)0 143 8210伽玛函数订正(集合)0 133 659多项式订正(集合)0 155 4114

因此，本文对CFSv2集合平均值分别进行伽玛函数订正以及多项式订正，改善由CFSv2计算得到的SA值严重偏小的情况，使SA值在异常事件出现时达到判别阈值，从而识别出异常事件，提高预报精度。与CFSv2集合平均得出的SA相比，订正后的CFSv2的SA值明显增大(图4)，而且Ts和异常值报对的次数有明显地提高，伽玛函数及多项式订正的Ts和异常值报对的次数分别为0.15和10次以及0.14和10次，但Bs也相应的误差增大(3.00、3.31)，从评价指标来看，伽玛函数订正的预报要优于多项式订正的。然而，选择何种订正方法以及Ts、Bs之间如何取舍、平衡需要根据实际情况权衡，有待进一步的研究。

对SA集合异常预报而言，也需对CFSv2集合成员进行误差的订正，再分别计算SA，取频率最大的SA值作为判别异常值的指标。基于多项式订正的预报报对的次数达到14次，然而Ts并没有显著提高(0.15)，Bs却有明显地增加(5.41)，而基于伽玛函数订正的预报并没有提高，不仅报对的次数及Ts对比集合平均没有显著增加(9次、0.13)，而且Bs误差增加了(3.65)。虽然集合异常预报与集合平均相比没有体现显著的优势，但集合异常预报最大的优点为可以给每个SA值赋予可信度值，即得到SA值的频率分布，从而为决策者的选择提供参考的信息。

3.3 SA与BMA的联合预报

BMA只能提供不同分位数的预报值，缺少选择时可供参考的客观信息，因此对不同分位数的选取可根据SA对异常值的识别作为参考来进行。

在与BMA对应的138次预报中(表3)，除CFSv2集合平均的Ts较小外(0.10)，其余的Ts均较好，在0.14以上，但Bs值也显著地增加，其中集合预报的多项式订正的Bs达到4.88，综合这两种评价指标，表现较好的是集合平均值的伽玛函数订正预报。

另外，对SA判断出现异常值时，选择BMA95%分位数预报值而实际也是95%分位数预报值要更优的情况，这5种预报的概率(频率)较为接近，除集合平均值的多项式订正预报概率(频率)略小外(0.26)，其余为0.28以上，最好的是CFSv2集合平均预报以及集合平均的伽玛函数订正预报(均为0.29)。而对SA判断不出现异常值时，选择75%分位数预报值而实际也是75%分位数预报值要更优的情况，除CFSv2集合平均预报的概率(频率)较小外(0.38)，其余预报方法概率(频率)均在0.75以上，最好的是集合的多项式订正预报(0.78)。综合而言，基于集合平均值的伽玛函数订正预报在这几种预报方法中是最优。值得注意的是，对于报对95%分位数的概率(频率)要明显低于75%分位数，这可能说明对于极端情况，无论是SA还是BMA都还存在误报的情况，而这种对极端情况误报的情况，在建立它们两者关系时可能会更加明显。

表3 SA误差情况及与BMA不同分位数联合预报情况1)

1)95%和75%分位数表示当SA判断异常或非异常时选择95%或75%分位数而实际也是95%或75%分位数更优时的概率(频率)

基于以上分析，SA与BMA之间可建立如下的关系，即当SA判断会出现异常值时大致可选择95%分位数的预报值，相反则选择75%分位数预报值，而这两种关系中，又以SA判断不出现异常值时选择75%分位数预报值这种情况的可靠性更高，其中基于集合平均值的伽玛函数订正预报在这几种预报方法中是最优的。

4 结 论

本文探讨BMA对CFSv2在东江流域汛期月降雨量预报的订正效果以及SA(包括确定性预报、集合预报以及对原始预报值的伽玛订正和多项式订正)对汛期异常月降雨量的识别，并建立SA和BMA结果之间的联系，得到如下结论：

1)BMA50%以下的分位数不具有预报作用，75%分位数具有最优的预报效果。应该注意的是，BMA也会出现误报的情况，尤其是极端降雨的预报，BMA还存在一些不足之处，常表现为对极端降雨的低估。

2) 利用CFSv2集合平均值进行SA计算时，SA严重偏小，可能说明CFSv2存在系统性误差。对CFSv2原始预报分别进行伽玛函数订正以及多项式订正后，Ts和异常值报对的次数有明显地提高，但Bs也相应地增大。从评价指标来看，伽玛函数订正的预报要优于多项式订正。

3)SA与BMA之间大致可建立如下的关系，即当SA判断会出现异常值时可选择95%分位数的预报值，相反则选择75%分位数预报值，而这两种关系中，又以SA判断不出现异常值时选择75%分位数预报值这种情况的可靠性更高，其中基于集合平均值的伽玛函数订正预报在这几种预报方法中是最优的。

通过SA和BMA的联合预报降雨相比以往纯粹使用CFSv2效果更好，也比单独使用BMA时能得到更多的客观信息从而能更好地选择相应的预报值，同时通过集合预报法以及与BMA的联合也改善了确定性预报中SA只能进行定性判别的不足。但也应注意到，SA和BMA本身也存在误报的缺点，而它们之间的联合预报也还有不确定性的地方，如何提高SA、BMA本身以及它们联合时的精度或定量刻画这种不确定性，都需要而且有必要进行进一步的研究。

[1]GUOJ,LIZ.ClassificationofmereorologicaldisastersandstrategiesforhazardpreventionandreductioninChina[J].JournalofCatastrophology, 2005, 20(4): 106-110.

[2]SILVESTROF,REBORAN.Impactofprecipitationforecastuncertaintiesandinitialsoilmoistureconditionsonaprobabilisticfloodforecastingchain[J].JournalofHydrology,2014,519:1052-1067.

[3]FOXG,TUMERJ,GILLESPIET.Thevalueofprecipitationforecastinformationinwinterwheatproduction[J].AgriculturalandForestMeteorology, 1999, 95(2): 99-111.

[4]DAVOLIOS,MIGLIETTAM,DIOMEDET,etal.Ameteo-hydrologicalpredictionsystembasedonamulti-modelapproachforprecipitationforecasting[J].NaturalHazardsandEarthSystemSciences,2008,8(1):143.

[5]HABETSF,LEMOIGNEP,NOILHANJ.Ontheutilityofoperationalprecipitationforecaststoservedasinputforstreamflowforecasting[J].JournalofHydrology, 2004, 293(1):270-288.

[6]ZHANGH,LINZ,ZENGQ.ThecomputationalschemeandthetestfordynamicalframeworkofIAPAGCM-4[J].ChineseJournalAtmosphericSciences,2009, 33(6):1267-1285.

[8]SAHA,S,NADIGAS,THIAWC,etal.TheNCEPclimateforecastsystem[J].JournalofClimate,2006,19(15):3483-3517.

[9]YUANX,WOOD,ERICF,etal.CFSv2-BasedseasonalhydroclimaticforecastsovertheconterminousUnitedStates[J].JournalofClimate,2013,26(13):4828-4847..

[10]SILVAG,DUTRAL,ROCHAR,etal.PreliminaryanalysisontheglobalfeaturesoftheNCEPCFSv2seasonalhindcasts[J].AdvancesinMeteorology, 2014,2014:21.

[11]JIANGX,YANGS,LIY,etal.Seasonal-to-interannualpredictionoftheAsiansummermonsoonintheNCEPclimateforecastsystemversion2[J].JournalofClimate,2013,26(11):3708-3727.

[12]GOSWAMIB,DESHPANDEM,MUKHOPADHYAYP,etal.SimulationofmonsoonintraseasonalvariabilityinNCEPCFSv2anditsroleonsystematicbias[J].ClimateDynamics,2014,43(9/10):2725-2745.

[13]LUOL,TANGW,LINZ,etal.EvaluationofsummertemperatureandprecipitationpredictionsfromNCEPCFSv2retrospectiveforecastoverChina[J].ClimateDynamics,2013,41(7/8):2213-2230.

[14]RAFTERYA,GENITINT,BALABDAOUIF,etal.UsingBayesianmodelaveragingtocalibrateforecastensembles[J].MonthlyWeatherReview, 2005, 133:1155-1174.

[15]SLOUGHTERJ,RAFTERYA,GENITINGT,etal.ProbabilisticquantitativeprecipitationforecastingusingBayesianmodelaveraging[J].MonthlyWeatherReview, 2007,135:3209-3220.

[16]KIMC,SUHM.ProspectsofusingBayesianmodelaveragingforthecalibrationofone-monthforecastsofsurfaceairtemperatureoverSouthKorea[J].Asia-PacificJournalofAtmosphericSciences, 2013, 49(3):301-311.

[17]LIUJ,XIEZ.BMAprobabilisticquantitativeprecipitationforecastingovertheHuaihebasinusingTIGGEmultimodelensembleforecasts[J].MonthlyWeatherReview, 2014, 142(4):1542-1555.

[18]PENGZ,WANGQ,BENNETTJ,etal.SeasonalprecipitationforecastsoverChinausingmonthlylarge-scaleoceanic-atmosphericindices[J].JournalofHydrology, 2014, 519:792-802.

[19]PENGZ,WANGQ,BENNETTJ,etal.StatisticalcalibrationandbridgingofECMWFSystem4outputsforforecastingseasonalprecipitationoverChina[J].JGeophysResAtmos,2014,119(12):7116-7135.

[20] 杜钧,GRUMMR,邓国.预报异常极端高影响天气的“集合异常预报法”：以北京2012年7月21日特大暴雨为例 [J]. 大气科学, 2014,38 (4): 685-699.

[21]SAHAS,MOORTHIS,PANH,etal.TheNCEPclimateforecastsystemreanalysis[J].BulletinoftheAmericanMeteorologicalSociety, 2010, 91(8):1015-1057.

[22]GOSWAMIB,DESHPANDEM,MUKHOPADHYAYP,etal.SimulationofmonsoonintraseasonalvariabilityinNCEPCFSv2anditsroleonsystematicbias[J].ClimateDynamics,2014,43(9/10):2725-2745.

[23]SAHAS,MOORTHIS,WUX,etal.TheNCEPclimateforecastsystemversion2[J].JournalofClimate,2014,27(6):2185-2208.

[24]MOLLERA,LENKOSKIA,THORDISL,etal.MultivariateprobabilisticforecastingusingensembleBayesianmodelaveragingandcopulas[J].QJRMeteorolSoc, 2013, 139(673):982-991.

[25]RAFTERYA,GENITINGT,BALABDAOUIF,etal.UsingBayesianmodelaveragingtocalibrateforecastensembles[J].MonthlyWeatherReview, 2005,133:1155-1174.

[26]SLOUGHTERJ,RAFTERYA,GENITINGT,etal.ProbabilisticquantitativeprecipitationforecastingusingBayesianmodelaveraging[J].MonthlyWeatherReview, 2007,135:3209-3220.

[27]YANGC,CHANDLERR,ISHAMV,etal.Spatial-temporalrainfallsimulationusinggeneralizedlinearmodels[J].WaterResourceResearch, 2005, 41(11):114-115.

[28]RENL,GLASUREY.Applicabilityoftherevisedmeanabsolutepercentageerrors(MAPE)approachtosomepopularnormalandnon-normalindependenttimeseries[J].InternationalAdvancesinEconomicResearch,2009,15(4):409-420.

[29]TINAG,FIORES,VENTURAC.Analysisofforecasterrorsforirradianceonthehorizontalplane[J].EnergyConversionandManagement,2012,64:533-540.

[30] 杜钧,李俊.集合预报方法在暴雨研究和预报中的应用[J].气象科技进展,2014(5):6-20.

Precipitation forecasting in flood season over the Dongjiang Basin using Bayesian model averaging and standardized anomaly

WUYuzhen,FENGZhizhou,WANGDagang

(Department of Water Resources and Environment, Sun Yat-sen University, Guangzhou 510275, China)

Bayesian Model Averaging (BMA) is applied to monthly precipitation forecasting in the flood season over the Dongjiang basin to correct the bias of Climate Forecast System version2 (CFSv2). In the meantime, Standardized Anomaly (SA) is used to quantify the precipitation abnormality and incorporated into the deterministic and ensemble forecasting. A better precipitation forecasting model is then established by the combination of BMA and SA to improve accuracy of long-term precipitation forecasting in the Dongjiang basin. Conclusions are drawn as follows: ① The 50th percentile and below of ensemble forecasting have poor skill , whereas the 75th percentile is usually in agreement with observations. However, BMA has disadvantage in that it underestimates precipitation amount when extreme events occur. ② The value of SA based on the ensemble average of CFSv2 is too small, indicating a systematic bias of CFSv2. When the CFSv2 raw forecasting is corrected by gamma function and multinomial, both Threat Score and the number of greatly increases but Bias Score increases in the meanwhile; ③ The relationship between SA and BMA can be expressed as follows: the 95th percentile of ensemble forecasting is used when SA indicates an abnormal precipitation, otherwise the 75th percentile is used.

BMA; SA; CFSv2; flood season; the Dongjiang basin

10.13471/j.cnki.acta.snus.2016.06.003

2016-02-25

国家自然科学基金资助项目(51379224);广东省水利科技创新基金资助项目(2014-11)；中山大学高校基本科研业务费专项资金资助项目(15lgjc)

吴裕珍(1991年生)，女；研究方向：气象气候预测;通讯作者：王大刚；E-mail:wangdag@mail.sysu.edu.cn

P456.7

A

0529-6579(2016)06-0020-08