一种基于熵增理论的疲劳-蠕变交互作用损伤模型及试验验证

陈　凌　张贤明　刘　飞　欧阳平　刘先斌

1.重庆工商大学废油资源化技术与装备教育部工程研究中心，重庆,4000672.重庆大学，重庆,400044



一种基于熵增理论的疲劳-蠕变交互作用损伤模型及试验验证

陈凌1,2张贤明1刘飞2欧阳平1刘先斌1

1.重庆工商大学废油资源化技术与装备教育部工程研究中心，重庆,4000672.重庆大学，重庆,400044

摘要：根据经典热力学理论，材料疲劳-蠕变交互作用下的损伤过程可视为系统熵增的累积，当熵增积累到临界值时，材料发生失效断裂。按此理论，并基于连续损伤力学和能量守恒定律，以系统熵增的变化来描述材料损伤，建立了一种疲劳-蠕变交互作用的损伤模型。为验证该模型，进行了540℃和520℃环境下1.25Cr-0.5Mo钢应力控制的梯形波加载试验，以材料的残余应变反映熵增积累，选取残余应变的变化作为损伤变量，用上述损伤模型进行了材料疲劳-蠕变交互作用的损伤演化描述，结果表明实测损伤点数据与该模型的损伤演化规律符合较好。

关键词：疲劳-蠕变；熵增；连续损伤力学；损伤变量；残余应变

0引言

石油化工、冶金、动力、航空航天等领域的高温承压设备在服役过程中通常承受疲劳和蠕变的交互作用，容易引发设备失效，疲劳-蠕变交互作用的损伤演化规律是这类设备进行安全评估的重要依据，一直以来受到国内外工程研究人员的关注。到目前为止，许多学者针对疲劳-蠕变交互作用的损伤演化进行了研究[1-9]，这类研究主要是基于经典的连续损伤力学(continuum damage mechanics，CDM)[10]理论，利用材料有效承载面积的减少定义损伤，分别计算疲劳和蠕变的损伤后进行叠加，再基于相应的假设建立损伤模型，结合合适的损伤变量对损伤演化进行描述。这类模型由于需要分别计算疲劳和蠕变的损伤再进行叠加，大都形式复杂，需要的参数较多，不便于实际应用，同时，一些基于相应假设的简化模型缺乏足够的理论基础。

针对上述情况，本文根据经典热力学理论，将材料疲劳-蠕变交互作用下的损伤过程视为系统熵增的累积，当熵增积累到临界值时，材料发生失效断裂。按此理论，并基于连续损伤力学和能量守恒定律，以系统熵增的变化来描述材料损伤，建立了一种疲劳-蠕变交互作用的损伤模型。为验证模型的准确性，进行了540℃和520℃环境下1.25Cr0.5Mo钢应力控制的梯形波加载试验，以材料的残余应变反映熵增积累，选取残余应变的变化作为损伤变量，用上述损伤模型进行了材料疲劳-蠕变交互作用的损伤演化描述。

1一种基于熵增理论的疲劳-蠕变交互作用损伤模型

根据经典热力学理论，熵是表征系统无序混乱程度的状态量，材料疲劳-蠕变交互作用下的损伤过程可视为系统熵增的积累，当熵增积累到临界值时，材料发生失效断裂。按此理论，材料疲劳-蠕变交互作用下的损伤可定义为

(1)

式中，D为材料损伤；ΔS为材料疲劳-蠕变交互作用过程中的单位质量熵增积累；ΔSf为材料疲劳-蠕变交互作用下失效破坏时的单位质量熵增积累临界值。

同时，根据经典热力学理论，物质的熵增定义为

(2)

式中，s为物质的单位质量熵；q为单位质量物质与外部环境之间的热量交换；T为绝对温度。

另外，对于金属材料等连续致密材料，其疲劳-蠕变交互作用的过程满足自然界的普遍定律——能量守恒定律[11]，即物体内能和动能的增量之和等于物体接受的热增量与作用于物体的机械功的增量之和。根据经典热力学理论，能量守恒定律的局部表达式可表示为[12]

(3)

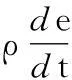
将式(2)代入式(3)中物体与外界的热量交换变化率(hi,i-ργ)，可得如下关系式：

(4)

将式(4)代入式(3)，可得

(5)

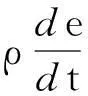
(6)

式中，W为机械功；ηW为机械功的内能转化率。

对于承受疲劳-蠕变交互作用的材料来说，每一循环过程中的弹性变形是可恢复的，而塑性变形是不可恢复的。因此，可认为材料每一循环过程中的熵增同材料的塑性变形相关，当塑性变形累积到一定程度时，材料的熵增积累达到临界值，材料即发生失效断裂。按此理论，根据式(6)，材料疲劳-蠕变交互作用下每一循环过程的熵增可表示为

(7)

式中，Δs为每一循环过程的单位质量熵增；Δtn为疲劳-蠕变交互作用下每一循环过程的时间；σeq为等效应力，与加载应力相关；Δεp为塑性应变范围。

对于疲劳-蠕变交互作用的加载过程来说，其塑性阶段的应力-应变曲线是非线性的。同时，对于金属材料等工程材料，其塑性阶段的应力-应变曲线大都符合幂强化力学模型[13]。因此，式(7)中的函数f(σeq,Δεp)可定义如下：

(8)

式中，m、 a、b为材料常数。

将式(8)代入式(7)，可得材料疲劳-蠕变交互作用下每一循环过程的单位质量熵增：

(9)

如前所述，材料疲劳-蠕变交互作用下的损伤过程可视为系统熵增的积累，因此，利用式(9)，对材料每一循环过程的单位质量熵增进行积分，可得材料疲劳-蠕变交互作用过程中的单位质量熵增积累：

(10)

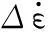
当循环周次N达到材料的失效寿命Nf时，ΔS即为ΔSf。

另外，基于式(1)，材料疲劳-蠕变交互作用下的损伤演化方程可定义如下：

(11)

将式(10)代入式(11)，可得

(12)

根据变上限定积分求导法则[14]，式(12)可改写为

(13)

根据经典损伤力学理论[10]，材料的损伤会导致有效承载面积减小使得应力增大。考虑到损伤对应力的影响，将式(13)改写为

(14)

对式(14)求积分，取积分上下限为D|N=0=D0，D|N=Nf=1，可得

D=1-(1-D0)(1-N/Nf)1/(a+1)

(15)

式中，D0为初始损伤。

对于材料疲劳-蠕变交互作用下的损伤演化，其损伤累积与加载应力和温度相关，因此，可用函数k(σ,T)代替式(15)中的1/(a+1)，将式(15)改写为

D=1-(1-D0)(1-N/Nf)k(σ,T)

(16)

其中，k(σ,T)为加载应力和温度的函数(简写为k)，用来反映疲劳-蠕变交互作用下的损伤累积程度。

式(16)即为基于熵增理论推导出的一种疲劳-蠕变交互作用损伤模型，该模型形式简单，理论依据明确，不需要大量的纯蠕变或纯疲劳试验来确定相关参数，非常便于实际应用。

2损伤变量选取

根据连续损伤力学，损伤变量是一种用于描述材料内部损伤状态变化发展及其对材料力学作用影响的内部状态变量[10]。如前所述，材料疲劳-蠕变交互作用下的损伤过程可视为系统熵增的积累，同时材料每一循环过程中的熵增同材料的塑性变形相关，当塑性变形累积到一定程度时，材料的熵增积累达到临界值，材料即发生失效断裂。材料每一循环的塑性变形积累会导致材料的残余应变增大，因此，可用材料的残余应变反映熵增积累。定义损伤变量为

(17)

式中，εrN为材料第N次循环后的残余应变；εrf为材料失效断裂时的残余应变。

式(17)所示的损伤变量，相比已有的选取弹性模量、割线模量及应变能密度等的变化作为损伤变量[15-18]来说，工程测量更为方便，具有较好的实时性，应用方便。

3试验结果及讨论

试验在岛津电液伺服疲劳试验机上进行，试验温度为540 ℃和520 ℃，采用螺纹夹持的1.25Cr0.5Mo珠光体耐热钢光滑圆棒试样，试样按国家标准GB/T15248-2008[19]制作。试验控制方式采用应力控制，为引入蠕变保载,采用梯形波加载，上下保载时间各为5s，加载频率0.05Hz。具体的试验条件及试验结果见表1、表2，其中Δσ为应力范围，σa为应力幅，σm为平均应力。

表1　540 ℃下材料疲劳-蠕变交互作用试验数据表

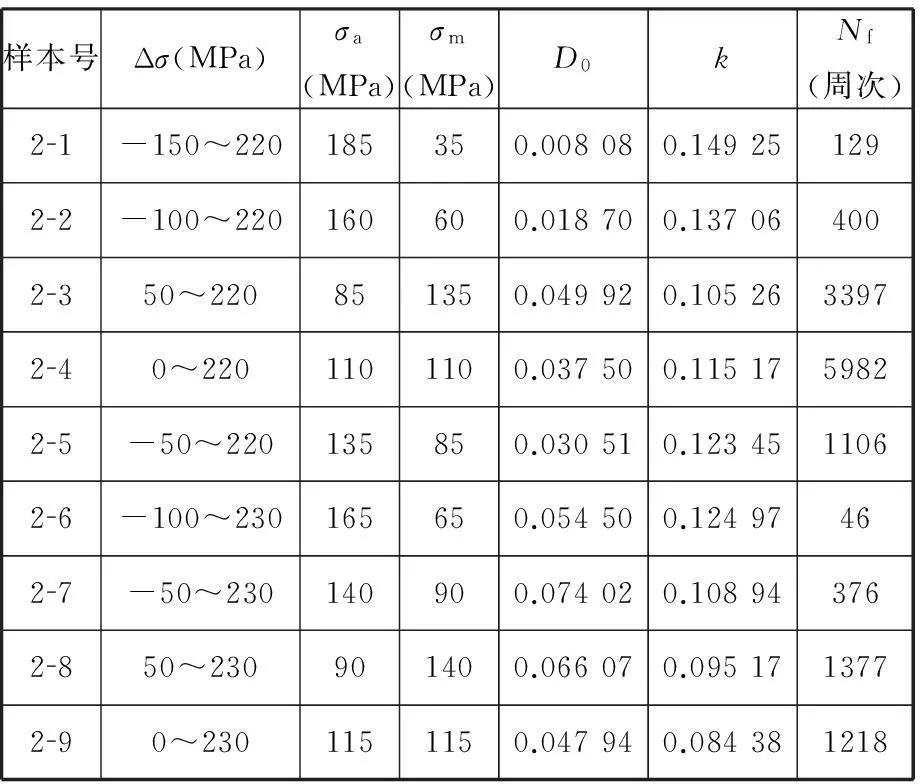
表2　520 ℃下材料疲劳-蠕变交互作用试验数据表

图1、图2分别为根据试验结果按式(17)所定义的损伤变量求得的1.25Cr0.5Mo钢在540 ℃和520 ℃环境下疲劳-蠕变交互作用下材料损伤的变化曲线，图中寿命分数φ=N/Nf。由图1、图2可知，材料的损伤在约80%寿命段区间内的增大速率变化不大，在循环后期随着塑性变形的积累导致材料的熵增积累逐渐接近临界值，损伤快速增大，当熵增积累达到临界值时，材料发生失效断裂。

图1　1.25Cr0.5Mo钢540 ℃疲劳-蠕变交互作用下的损伤变化曲线

在式(16)所示损伤模型中，以寿命分数φ=N/Nf为横轴、损伤D为纵轴，材料的损伤根据试验结果按式(17)所定义的损伤变量进行计算，可拟合求得1.25Cr0.5Mo钢在540 ℃和520 ℃环境下各样本的损伤模型和损伤曲线，拟合图见图3、图4(仅给出了代表性的拟合图)，拟合结果见表1、表2。

图2　1.25Cr0.5Mo钢520 ℃疲劳-蠕变交互作用下的损伤变化曲线

(a)1-1号样本　　 　　　　　　　　(b)1-3号样本　 　　　　　　　　　(c)1-5号样本

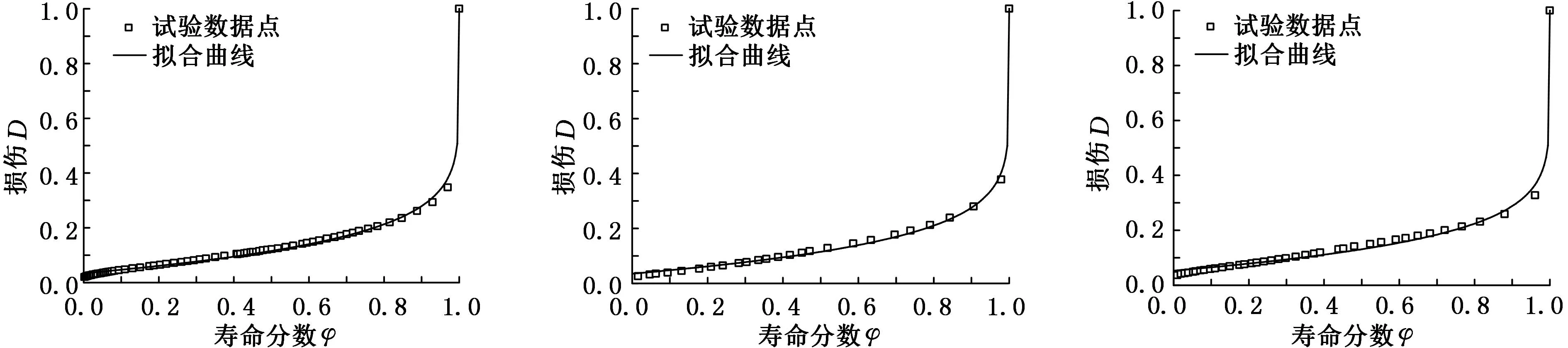
(d)1-7号样本　　 　　　　　　　　(e)1-9号样本　 　　　　　　　　　(f)1-11号样本图3　1.25Cr0.5Mo钢540 ℃疲劳-蠕变交互作用损伤模型拟合图

从图3、图4中可以看出，用材料的残余应变反映熵增积累，选取材料残余应变的变化作为损伤变量，按式(16)所示损伤模型拟合得到的损伤曲线与试验实测损伤点数据的符合程度较好，能够较好地描述材料的损伤演化。

另外，如前所述，式(16)中的材料常数k为加载应力和温度的函数，在一定的温度下，k为加载应力的函数，与加载的最大应力、应力幅、保载时间等因素相关。由于加载的最大应力σmax、应力幅σa和平均应力σm具有σm=σmax-σa的关系，所以，当保载时间固定时，在最大应力相差不大的情况下，可用平均应力来反映最大应力和应力幅的影响，将k简化为平均应力的函数。

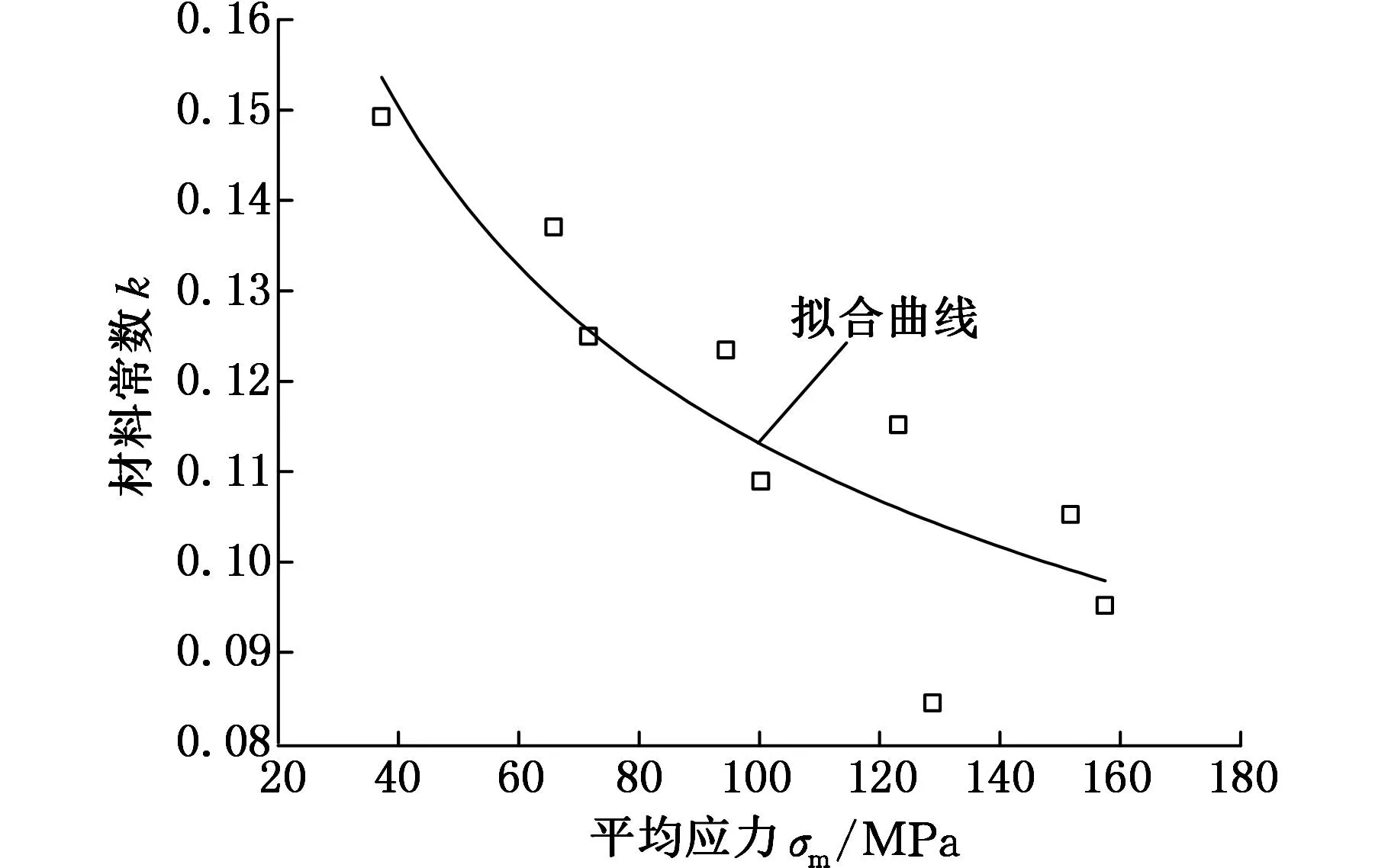
图5给出了1.25Cr0.5Mo钢在540 ℃、520℃ 时各工况下k随平均应力的变化趋势。由图5可知，材料常数k随平均应力的增大而减小，其减小趋势与幂函数形势较为符合，用幂函数对其进行拟合，拟合曲线见图5，拟合关系式如下：

540 ℃时

(18)

520 ℃时

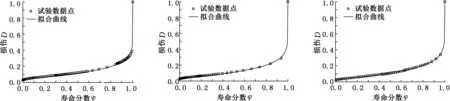
(a)2-3号样本　　 　　　　　　　　(b)2-4号样本　 　　　　　　　　　(c)2-5号样本

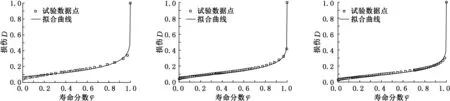
(d)2-7号样本　　 　　　　　　　　(e)2-8号样本　 　　　　　　　　　(f)2-9号样本图4　1.25Cr0.5Mo钢在520 ℃疲劳-蠕变交互作用损伤模型拟合图

(19)将式(18)、式(19)代入式(16)，即可得1.25Cr0.5Mo钢在540 ℃、520 ℃环境下疲劳-蠕变交互作用的损伤模型如下：

540 ℃时

520 ℃时

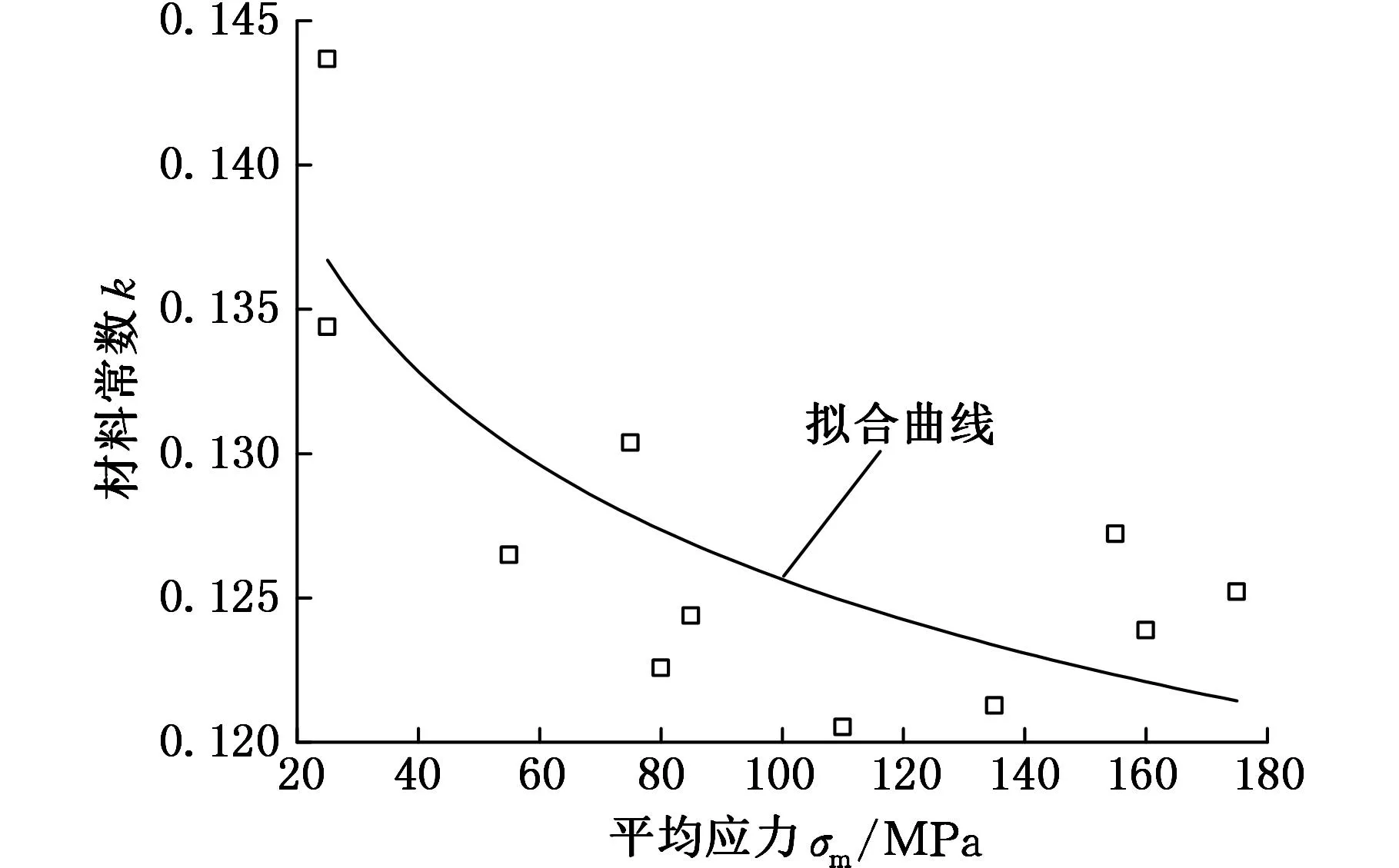
(a)　温度540℃

(b)温度520℃图5　k随平均应力的变化及拟合图

由上述分析可知，该损伤模型能够较好地描述材料的损伤演化，同时该模型形式简单，理论依据明确，具有较好的实际应用价值。

4结论

(1)根据经典热力学理论，将材料疲劳-蠕变交互作用下的损伤过程视为系统熵增的积累，当熵增积累到临界值时，材料发生失效断裂。按此理论，并基于连续损伤力学和能量守恒定律，以系统熵增的变化来描述材料损伤，建立了一种疲劳-蠕变交互作用的损伤模型：

D=1-(1-D0)(1-N/Nf)k(σ,T)

该模型形式简单，理论依据明确，不需要大量的纯蠕变或纯疲劳试验来确定相关参数，非常便于实际应用。

(2)进行了540 ℃和520 ℃环境下1.25Cr-0.5Mo钢应力控制的梯形波加载试验，以材料的残余应变反映熵增积累，选取残余应变的变化作为损伤变量，用上述损伤模型进行了材料疲劳-蠕变交互作用的损伤演化描述，结果表明，试验实测损伤点数据与该模型的损伤演化规律符合较好，该模型能够较好地描述材料的损伤演化。

参考文献：

[1]姚华堂, 轩福贞, 王正东, 等. 基于连续损伤理论的多轴蠕变设计[J]. 中国机械工程, 2007, 18(12):1439-1443.

YaoHuatang,XuanFuzhen,WangZhengdong,etal.MultiaxialCreepDesignBasedontheContinuumDamageTheory[J].ChinaMechanicalEngineering, 2007, 18(12):1439-1443.

[2]陈凌, 张贤明, 欧阳平. 一种疲劳-蠕变交互作用寿命预测模型及试验验证[J]. 中国机械工程, 2015, 26(10):1356-1361.

ChenLing,ZhangXianming,OuyangPing.AModelofLifePredictionforFatigue-creepInteractionandItsExperimentalVerification[J].ChinaMechanicalEngineering, 2015, 26(10):1356-1361.

[3]GharadaAE,ZedirabH,AzaribZ,etal.ASynergisticCreepFatigueFailureModelDamage(CaseoftheAlloyZ5NCTAat550℃) [J].EngineeringFractureMechanics, 2006, 73(6):750-770.

[4]朱顺鹏, 黄洪钟, 何俐萍, 等. 高温低周疲劳-蠕变的改进型广义应变能损伤函数方法[J]. 航空学报, 2011, 32(8):1445-1452.

ZhuShunpeng,HuangHongzhong,HeLiping,etal.ImprovedGeneralizedStrainEnergyDamageFunctionMethodforHighTemperatureLowCycleFatigue-creep[J].ActaAeronauticaetAstronauticaSinica, 2011, 32(8):1145-1452.

[5]胡绪腾, 马晓健, 宋迎东. 含保载弹性应力循环下TA12钛合金缺口试样的蠕变疲劳损伤分析[J]. 机械工程材料, 2013, 37(3):90-94.

HuXuteng,MaXiaojian,SongYingdong.Creep-FatigueDamageAnalysisofTA12TitaniumAlloyNotchedSampleatElasticStressCyclewithDwellTime[J].MaterialsforMechanicalEngineering, 2013, 37(3):90-94.

[6]LeilaJL,AbhijitD.AMeso-scaleDamageEvolutionModelforCyclicFatigueofViscoplasticMaterials[J].InternationalJournalofFatigue, 2009, 31(4):703-711.

[7]SullivanRW.DevelopmentofaViscoelasticContinuumDamageModelforCyclicLoading[J].MechanicsofTime-DependentMaterials, 2008, 12(4):329-342.

[8]徐建刚, 许金余. 粉末冶金材料空穴和夹杂的疲劳蠕变损伤分析[J]. 热加工工艺, 2013, 42(16):61-63,66.

XuJiangang,XuJinyu.AnalysisonFatigueandCreepDamageofPowderMetallurgyMaterialwithVoidandInclusion[J].HotWorkingTechnology, 2013, 42(16):61-63,66.

[9]WenJF,TuST.AMultiaxialCreep-damageModelforCreepCrackGrowthConsideringCavityGrowthandMicrocrackInteraction[J].EngineeringFractureMechanics, 2014, 123:197-210.

[10]沈为. 损伤力学[M]. 武汉: 华中理工大学出版社, 1995.

[11]杨光松. 损伤力学与复合材料损伤[M]. 北京: 国防工业出版社, 1995.

[12]ChenL,JiangJL,FanZC,etal.ANewModelforLifePredictionofFatigue-creepInteraction[J].InternationalJournalofFatigue, 2007, 29(4):615-619.

[13]毕继红. 工程弹塑性力学[M]. 天津: 天津大学出版社, 2003.

[14]吴迪光, 张彬. 微积分学(上)[M]. 杭州: 浙江大学出版社, 1995.

[15]LemaitreJ.AContinuousDamageMechanicsModelforDuctileFracture[J].JournalofEngineeringMaterialTechnology, 1985, 107(1):83-89.

[16]YangXH,LiN,JinZH,etal.AContinuousLowCycleFatigueDamageModelandItsApplicationinEngineeringMaterials[J].InternationalJournalofFatigue, 1997, 19(10):687-692.

[17]范志超, 蒋家羚, 陈学东. 16MnR钢疲劳与循环蠕变交互作用损伤力学模型[J]. 浙江大学学报(工学版), 2006, 40(2):317-321.

FanZhichao,JiangJialing,ChenXuedong.ContinuumDamageMechanicsModelofInteractionbetweenFatigueandCyclicCreepof16MnRSteel[J].JournalofZhejiangUniversity(EngineeringScience), 2006, 40(2):317-321.

[18]DjebliA,AidA,BendoubaM,etal.ANon-linearEnergyModelofFatigueDamageAccumulationandItsVerificationforAl-2024AluminumAlloy[J].InternationalJournalofNon-linearMechanics, 2013, 51:145-151.

[19]中国国家标准化管理委员会,GB/T15248-2008 金属材料轴向等幅低循环疲劳试验方法[S]. 北京: 中国标准出版社, 2008.

(编辑苏卫国)

A Damage Model for Fatigue-creep Interaction Based on Entropy Increase Theory and Its Experimental Verification

Chen Ling1, 2Zhang Xianming1Liu Fei2Ouyang Ping1Liu Xianbin1

1.Engineering Research Center for Waste Oil Recovery Technology and Equipment of Ministry of Education, Chongqing Technology and Business University, Chongqing, 400067 2.Chongqing University, Chongqing, 400044

Abstract:According to the classical theory of thermodynamics, the fatigue-creep interaction damage of the material might be regarded as the accumulation of the entropy increase. When this accumulation reached to the critical point, the failure occured. From this theory, using the change of the entropy increase to describe the material damage, a damage model for fatigue-creep interaction was developed herein based on CDM and the law of energy conservation. To verify this damage model, the fatigue-creep interaction tests of 1.25Cr0.5Mo steel were conducted with the trapezoidal wave loading under stress control at 540℃ and 520℃. According to the tests, the change of the residual strain, which might reflect the accumulation of the entropy increase of the material, was defined as the damage variable. With this definition, the damage curves of different loading conditions were obtained by the above fatigue-creep interaction damage model. Results show that the damage values measured from experiments are in good agreement with these damage curves, which means that the damage model presented herein may describe the fatigue-creep interaction damage evolution well.

Key words:fatigue-creep; entropy increase; continuum damage mechanics(CDM); damage variable; residual strain

收稿日期：2015-07-02

基金项目：中国博士后科学基金资助项目(2015M582523)；国家自然科学基金资助项目(51375516)；重庆市教委科学技术研究项目(KJ1500624)；教育部平台科技项目(fykf201502)；重庆工商大学科研启动经费资助项目(2014-56-10)

中图分类号：O346.5，TG115.5

DOI：10.3969/j.issn.1004-132X.2016.10.019

作者简介：陈凌，男，1979年生。重庆工商大学废油资源化技术与装备教育部工程研究中心高级工程师,重庆大学机械工程学院博士后研究人员。主要研究方向为金属材料的疲劳、断裂、腐蚀及机械结构安全评估。获中国发明专利10项。发表论文50余篇。张贤明，男，1955年生。重庆工商大学废油资源化技术与装备教育部工程研究中心教授。刘飞，男，1948年生。重庆大学机械工程学院教授、博士研究生导师。欧阳平，男，1979年生。重庆工商大学废油资源化技术与装备教育部工程研究中心副研究员。刘先斌，男，1961年生。重庆工商大学废油资源化技术与装备教育部工程研究中心教授。