分数阶微分增强的脑部MRI图像边缘检测
2016-06-02张艳珠王凡迪朱啸天
张艳珠,王凡迪,朱啸天
(沈阳理工大学 信息科学与工程学院,沈阳 110159)
分数阶微分增强的脑部MRI图像边缘检测
张艳珠,王凡迪,朱啸天
(沈阳理工大学 信息科学与工程学院,沈阳 110159)
摘要:针对传统边缘检测方法提取医学图像的边缘不理想问题,利用分数阶微分掩模算子预先对图像边缘做增强处理,同时根据分形理论,将可调的分数阶微分阶次与能够反应图像自身特点的分形维数相结合,提出脑部MRI图像的分数阶微分阶次和分形维数之间的对应关系,从而在微分阶次区间内选出最佳微分阶数,使得图像更利于细节边缘提取。通过仿真对比,由该方法检测出的脑部MRI图像边缘比传统整数阶提取的更加细致,保留更多的纹理细节。
关键词:边缘检测;脑部MRI;分数阶微分;分形理论
在医学领域,图像增强及边缘检测是最重要的图像处理方法[1-2]。对于脑部MRI图像的边缘检测,其边缘细节的清晰度会影响后续图像分割及分析研究。目前,在图像边缘检测领域有诸如Prewitt算子等经典的整数阶算法,但其结果都会受到图像自身纹理复杂度以及噪声信号的影响而导致中低频信号无法得到保留,造成相当一部分的信息缺失。针对整数阶微分算子检测边缘的缺点,蒲亦非等[3]将分数阶微分引入数字图像处理,论述了对于纹理细节信息丰富的图像而言,分数阶微分对灰度变化不大的平滑区域的增强明显优于整数阶微分运算。
为了使分数阶微分掩模算子足够增强图像纹理,如何选取合适的微分阶次来构造微分掩模是关键。据此本文首先结合分形理论[4],将分形维数应用到分数阶微分阶次的选取上,构造微分掩模来增强图像纹理;再结合整数阶边缘检测算法提取图像边缘。通过验证,本文的分数阶微分掩模算子对图像纹理信息具有极大的增强效果,更有利于边缘检测的细化。
1分数阶微分定义及算子掩模
1.1分数阶微分的定义
分数阶微分其实是整数阶微分在实数范围内的一个扩展,将微分阶次扩展到了分数。然而关于分数阶微分的定义,许多数学家从不同角度入手,给出了不同的定义。本文采用最原始的G-L定义,根据Hospital法则[4-6],假设存在一个可导函数f(t),利用法则就可以得到函数f(t)的一到三阶导数。
(1)
(2)

(3)
利用数学归纳法,可导函数f(t)的n(n∈N)阶导数为
(4)
为便于计算,引入Gamma函数[6],并将微分阶次从整数推广到分数,假设函数f(t)在区间[a,t]上存在n+1阶导数,那么对于任意的实数γ,利用微分的有限记忆功能,可推导出γ阶微分定义:
(5)
从以上推导可知,分数阶微分是由整数阶微分衍生而来,其运算结果与过去各点的距离都存在反比关系,而整数阶微分的记忆功能只与最近的几个点相关。这就是分数阶微分强大的记忆存储功能,因此分数阶微分能够保留更多图像纹理信息。
1.2分数阶微分掩模
将分数阶微分定义的连续表达式改写为差分表达式,并定义二维信号在x方向和y方向的分数阶微分的差分表达式[7]:
(6)
(7)
利用上述差分表达式进行掩模近似构造。为尽量减小滤波误差,选取分数阶微分差分表达式的前三项系数1、-v、(v2-v)/2构造掩模[8-9]。图1为传统的8方向Titans[9]掩模算子,具有一定的运算精度,该模板中最外层有8个位置为“0”。

(v2-v)/20(v2-v)/20(v2-v)/20-v-v-v0(v2-v)/2-v8-v(v2-v)/20-v-v-v0(v2-v)/20(v2-v)/20(v2-v)/2
图1分数阶微分8方向掩模
为了进一步提高算法的运算精度,增强算法的抗旋转性能。在Titans算子基础上,利用向量合成法合成新数据,替换“0”值,这样就会在原始基础上新增8个运算方向,分别夹在每两个原始方向之间,将经典的Titans掩模扩展为16方向的微分掩模。将分数阶微分的差分表达式中第一项系数添加到掩模的中心位置,第三项系数(v2-v)/2取代传统掩模“0”位置,第二项系数结合三角函数作向量分解计算。扩展后的16方向微分掩模[10]如图2所示。观察掩模模板,其参数变量只有一个,即分数阶微分阶次v,掩模对图像的处理效果随v的变化而不同。一般v的值是通过人工试探性地选取,这种方式在精确度上没有保证。为了提高选取v值的效率,本文后续将结合分形理论,通过能够反映图像自身特点的分形维数来选择分数阶微分阶次v的取值。

(v2—v)/2(v2—v)/2(v2—v)/2(v2—v)/2(v2—v)/2(v2—v)/2-2.0824v-2.0824v-2.0824v(v2—v)/2(v2—v)/2-2.0824v16-2.0824v(v2—v)/2(v2—v)/2-2.0824v-2.0824v-2.0824v(v2—v)/2(v2—v)/2(v2—v)/2(v2—v)/2(v2—v)/2(v2—v)/2
图2扩展的分数阶微分掩模
2分数阶微分掩模参数的选定
2.1脑部MRI图像分形维数算法
对于本文脑部MRI图像,先将其转化为二值图像,转化后的图像灰度值只有0和1。采用像素点覆盖的盒维数算法[11]来计算该图像的分形维数。具体算法如下:
(1)将图像二值化处理,得到一个数字矩阵,其行列数对应二值图的行列数;
(2)把得到的数字矩阵划分成大小相等的若干子块,使每一块的行数与列数均为r,把所有包含1的子块个数记作Nr,通常取r=1,2,4,…2i,即以1,2,…2i个像素点的尺寸为块的边长来划分,从而得到盒子数N1,N2,…,N2i。
由于像素点的尺寸δ=图像长度L/图像一行中像素点的个数,所以行与列像素点个数均为r的块的边长应为δr=rδ(r=1,2,4,…2i)。在双对数坐标平面内,用最小二乘法直线拟合数据点(logδr,logNr),(r=1,2,4,…2i)。所得到的直线斜率负值D就是图像的理论分形维数。
利用Matlab 7.10.0(R2010a) 软件进行仿真,操作界面如图3a所示。本文选取的脑部MRI原始图像如图3b所示。
利用二维数字图像像素点覆盖的分形盒维数算法,计算脑部MRI图像自身的分形维数。如图3c所示的分形盒维数曲线,拟合曲线方程y=kx+b,其中斜率|k|近似等于分形维数D,即D=|k|,仿真结果如图3a。其中包含像素值为“1”的盒子数为N=4653。拟合曲线y=2.2419x+19.279从而可知分形维数D=|k|=2.2419。

(a)Matlab(R2010a)操作界面
(b)原图
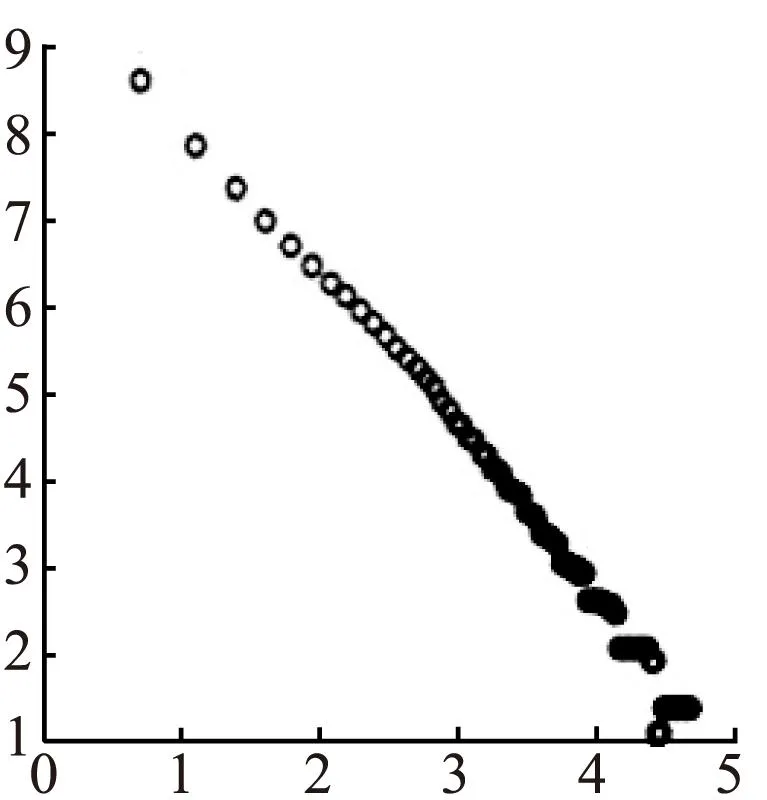
(c)盒维数拟合曲线
2.2分形维数及分数阶微分阶次的选择
文献[11-12]通过对纹理图像的研究,证明了灰度图像是具有相同分形特征的分形表面,一幅二维数字图像三维空间坐标为(x,y,f(x,y)),其中f(x,y)代表图像中像素点(x,y)处的灰度值。一幅图像的分形维数可以作为该图像自身的特征。本文将图像的维数特征映射到分数阶微分掩模参数上,找到一种合适的映射关系,可以自适应选取分数阶微分阶次,从而高效率地对图像做分数阶微分处理。
对分数阶微分掩膜算子的参数进行选定时,首先计算出图像的分形维数D,通常二维数字图像分形维数区间D∈(2,3),而由分数阶微分G-L定义可知分数阶微分的阶次v∈(0,1),所以需要把区间(2,3)映射到区间(0,1)上,据此,映射途径有两种:(1)v=D-2;(2)v=3-D。根据本文选取的脑部MRI图像来说,当分别选择这两种途径时,提取的图像轮廓线分别如图4a、图4b所示。
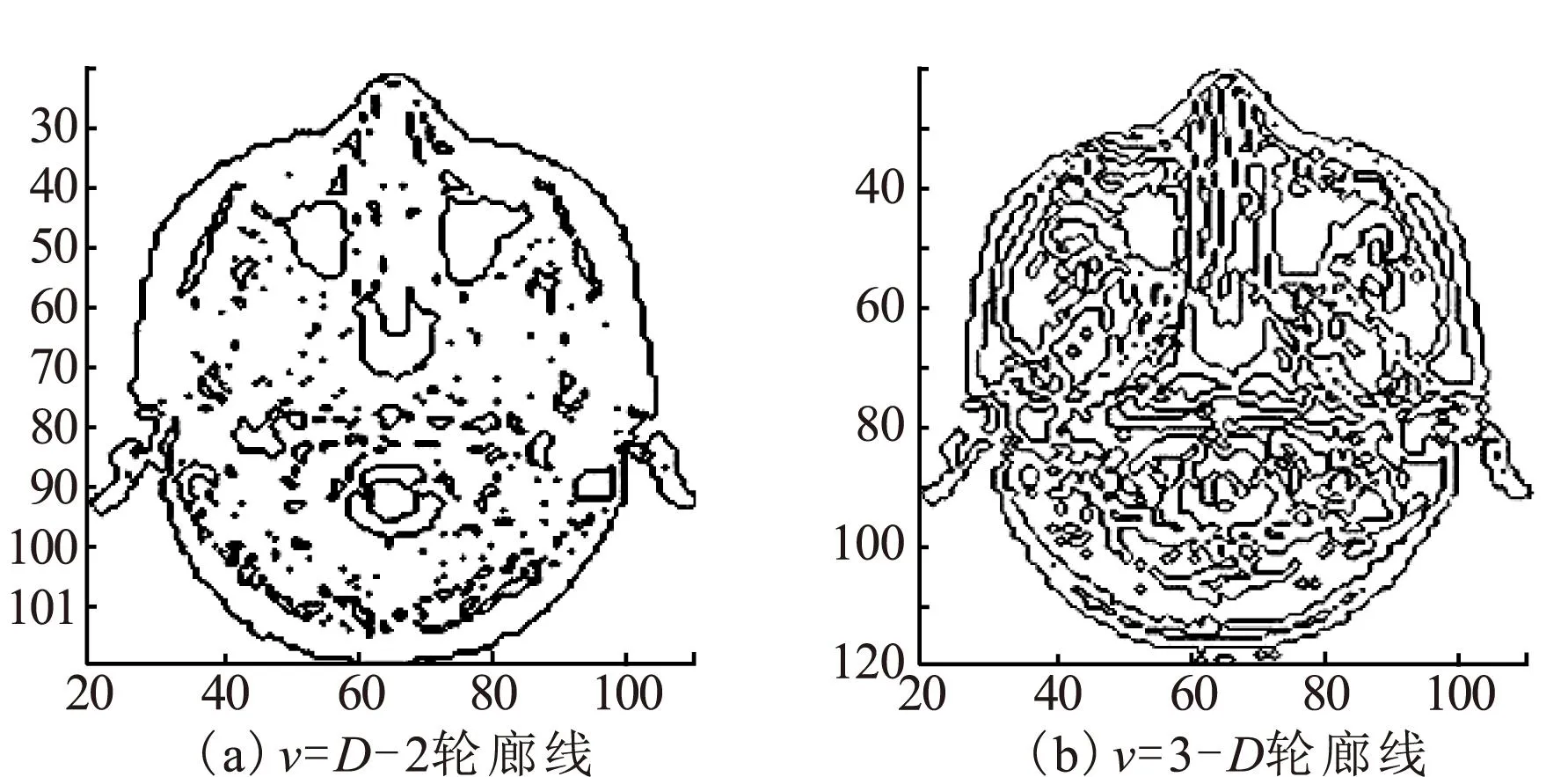
图4 图像轮廓线
通过对比图4a、4b可知,当取v=3-D时,能保留更多细节信息。因此本文所采用的映射关系为:v=3-D,其中,D代表图像分形维数,v代表分数阶微分阶数。分数阶微分掩模参数选定流程如图5所示。
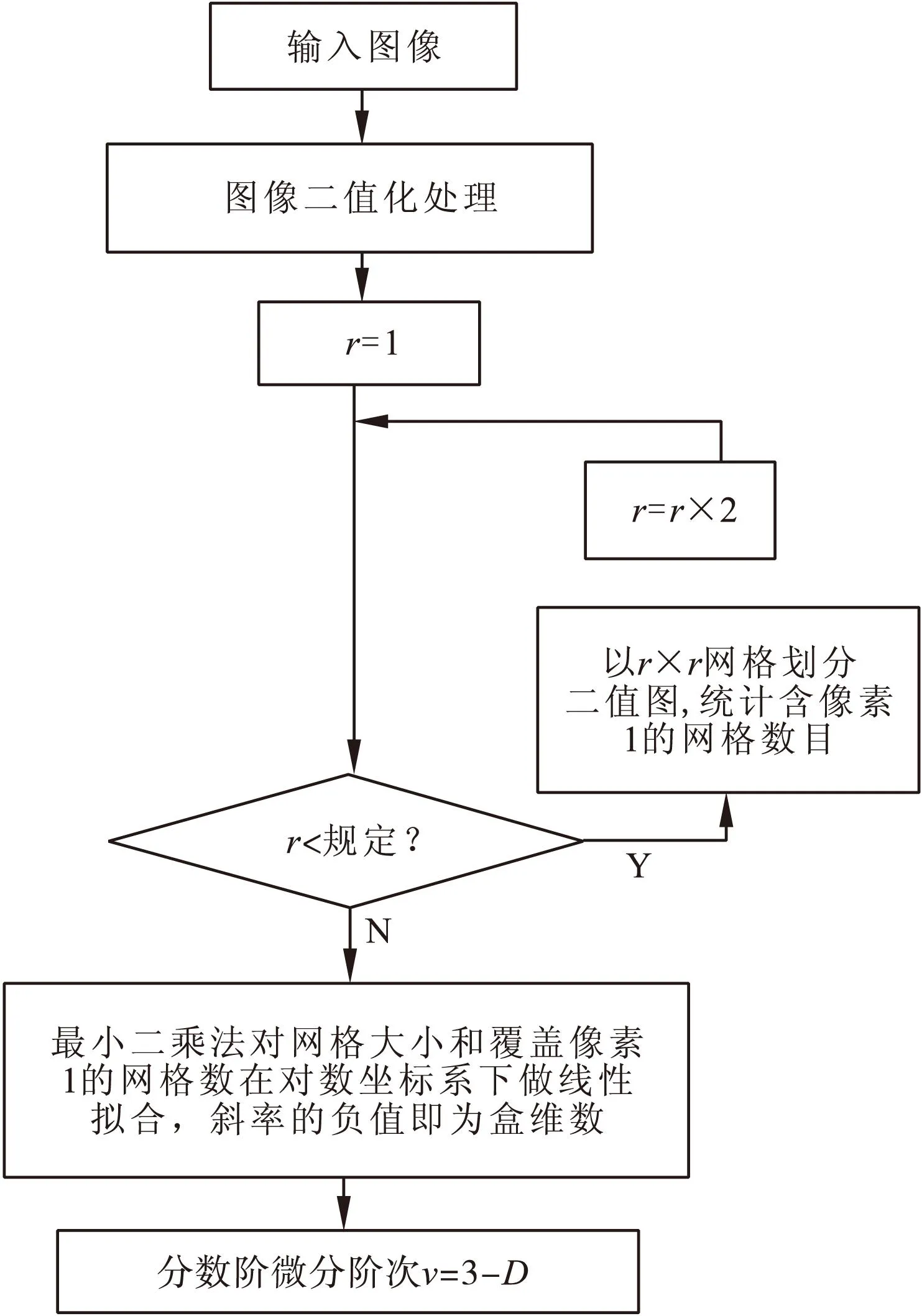
图5 分数阶微分掩模参数选定流程图
3脑部MRI图像边缘检测分析
首先采用传统的整数阶微分边缘检测方法检测脑部MRI图像边缘,其次根据本文采用的映射关系v=3-D(由前文计算得到D=2.2419),选择对应的分数阶微分阶次:v=3-D=0.7581,该微分阶次包含在理论区间范围v∈(0,1),因此取值合理。
依据选定的分数阶微分阶次构造微分掩模,对图像做卷积处理,使图像得到增强,卷积处理后的图像如图6所示。

图6 分数阶微分后的图像
最后,结合传统整数阶边缘检测算法提取图像边缘。将两种检测结果相对比,如图 7所示。

(a)sobel边缘检测

(b)微分后的sobel边缘
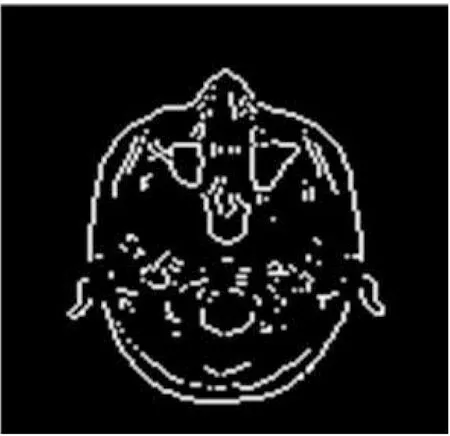
(c)prewitt边缘检测

(d)微分后的prewitt边缘

(e)canny边缘检测

(f)微分后的canny边缘
图7a、7c、7e分别为整数阶Sobel算子、Prewitt算子及Canny算子对脑部MRI图像进行边缘检测的结果;图7b、7d、7f分别表示经过分数阶微分算子增强之后再对脑部MRI图像进行边缘提取的结果。
Haralick等人及国内学者[13-14]从理论上论证了熵值能体现图像纹理特征。熵值越大,信息量越大,纹理越丰富。表1中记录了通过分数阶掩模增强前后边缘图像的信息熵值。

表1 图像熵值对比
对比可知,经过分数阶微分掩模算子增强后的图像熵值有所增大,表明利用分形维数选取的分数阶微分掩模算子对图像有很好的增强作用,保留了原图像中更多的纹理信息。提高了边缘细节的清晰度,有利于脑部结构分析,同时也为脑部结构的分割工作做准备。
4结束语
将分形理论融合进掩模参数选定过程中,根据图像自身的分形维数,找到维数与分数阶微分阶次的映射关系,从而缩短微分阶次的选定时间。实验结果证明,结合分形理论来取得的分数阶微分阶次可以提高图像处理效率,符合人眼视觉需求,提取出的图像边缘更加丰富和清晰。研究只针对脑部MRI图像,其分形维数与微分阶次的对应关系有一定局限性,未来有待更深入地研究。
参考文献:
[1]蒲亦非,周激流,廖科.分数阶微积分原理及其在现代信号分析与处理中的应用[M].北京:科学出版社,2010:89-145.
[2]薛文格,邝天福.图像边缘检测方法研究[J].多媒体技术及其应用,2007,14(16):1144-1145.
[3]罗强,任庆利,杨万海.基于分形理论的图像边缘提取方法[J].通信学报,2001,18(11):104-109.
[4]蒲亦非,王卫星.数字图像的分数阶微分掩模及其数值运算规则[J].自动化学报,2007,33(11) :1129-1135.
[5]王宏,赵海滨.数字图像处理[M].沈阳:东北大学出版社,2005:62-70.
[6]孙即祥.图像分析[M].北京:科学出版社,2005:16-21.
[7]蒲亦非.将分数阶微分演算引入数字图像处理[J].四川大学学报:工程科学版,2007,39(3):124-132.
[8]杨柱中,周激流,黄梅.基于分数阶微分的边缘检测[J].四川大学学报:工程科学版,2008,40(1):152-157.
[9]杨柱中,周激流.基于分数阶微分的图像增强[J].计算机辅助设计与图形学学报,2008,20(3):343-348.
[10]车进,师一帅.基于分数阶微分的视网膜血管图像增强[J].计算机工程与应用,2012,47(34):162-165.
[11]PENTLAND A P.Fractal—Based Description of Natural Scenes[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,1984,6(6):661-674.
[12]丁保华,李文超,王福明.分形图像分析与分形维数计算程序的设计[J].北京科技大学学报,1999,21(3):304-307.
[13]PENTLAND A P.Shading into texture[J].Artificial Intelligence,1986,17(29):147-170.
[14]HARALICK R M,SHANMUGAM K.Textural features for image classification[J].IEEE Trans on Systems,Man,and Cybernetics,1973,90(6):610-621.
(责任编辑:马金发)
Brain MRI Image Edge Detection Based on Fractional Differentiation
ZHANG Yanzhu,WANG Fandi,ZHU Xiaotian
(Shenyang Ligong University,Shenyang 110159,China)
Abstract:Traditional edge detection method in medical image edge is not ideal,fractional differential mask operator is proposed firstly to enhance the image,which combines the adjustable.Fractional differential order with fractal dimension reflects characteristics of images and an corresponding relationship is found out between them according is to the fractal theory,thus the best differential order is efficiently chosen,which is more conductive to detect image edge.The simulation results show that the proposed method can extract more meticulously and retain more texture details than traditional integer order in detecting the edge of brain MRI image.
Key words:edge detection;brain MRI;fractional differential;fractal theory
中图分类号:TP391
文献标志码:A
文章编号:1003-1251(2016)02-0030-05
作者简介:张艳珠( 1971—) ,女,副教授,博士,研究方向:目标识别,分数阶控制,智能算法。
收稿日期:2015-04-03
