重力补偿的机械臂轨迹跟踪研究
2016-06-02李宏达
姜 静,曹 松,李宏达
(沈阳理工大学 信息科学与工程学院,沈阳 110159)
重力补偿的机械臂轨迹跟踪研究
姜静,曹松,李宏达
(沈阳理工大学 信息科学与工程学院,沈阳 110159)
摘要:针对隧道掘进工程中某喷涂机械臂的控制精度问题,研究了基于重力补偿的机械臂PD与PID的控制方法。分析了这两种机械臂轨迹跟踪算法的稳定性与收敛性:基于重力补偿的PD控制算法是全局渐进稳定的,而PID控制算法在某些条件下是半全局渐进稳定的。计算机仿真结果表明,PD控制关节最大误差为0.14rad,PID控制关节最大误差为0.05rad,这两种算法都能够实现机械臂运动轨迹的准确跟踪,满足机械臂的位置控制要求,表明控制方法的有效性。
关键词:机械臂; PID控制;重力补偿;轨迹跟踪
随着科学技术的发展,机械臂在工业生产过程中发挥着越来越重要的作用。尤其是在面对复杂工况、恶劣的不可预测的工作环境、甚至是人类无法到达的危险地域执行任务时,发挥着不可替代的作用。机械臂控制的目的是位置控制问题,即控制机械臂手端的位置和姿态(也可称为期望轨迹或期望位置)。期望轨迹通常有两种形式:一种是固定位置;另一种是一条随时间连续变化的轨迹。本文研究轨迹跟踪问题。机械臂的控制方法按照其控制器是否考虑动力学特性分为两类:一类是完全不考虑机械臂的动力学特性,即所谓的运动控制;另一类为根据动力学模型的性质设计出非线性控制律,即所谓的动态控制。目前绝大多数工业机械臂采用PD和PID控制算法[1],原理简单,实用性较强。现在,许多专家与学者应用各种智能控制方法与传统PID算法相结合[2-3],对算法进行改进,研究分析其对机械臂的控制精度及轨迹跟踪性能产生影响,期望能达到更好的控制效果。本文从不同的角度对这两种算法的稳定性进行讨论和研究,并在仿真实验中比较分析了两种算法的控制效果。
1PID控制原理
PID控制算法具有控制简单,易于实现,无需建模等优点,PID控制器由比例、积分、微分环节所组成,其控制原理如图1所示[4]。PID控制器算式如下:
(1)
式中:e为被控量与设定值的偏差;u(t)为控制输出量;KP、KI、KD分别为比例、积分、微分系数。
各个环节对系统性能的影响:
比例环节—成比例的反应偏差信号,如果有偏差产生,控制器立即会发生作用。其主要特点是作用快,无法彻底消除误差。
积分环节—只要有控制偏差存在,积分控制就会逐渐增强其作用,直至消除控制偏差。其主要特点是积分效果缓慢,能够彻底消除误差,但其稳定性相比比例控制要差,在控制时间上表现为“过去效应”。
微分环节——能够反映控制偏差的变化趋势,以此来调节控制器的输出。其主要特点是调节十分迅速,但是对系统的干扰比较敏感,因此会降低系统的抗干扰能力,在控制时间上表现为“将来效应”。
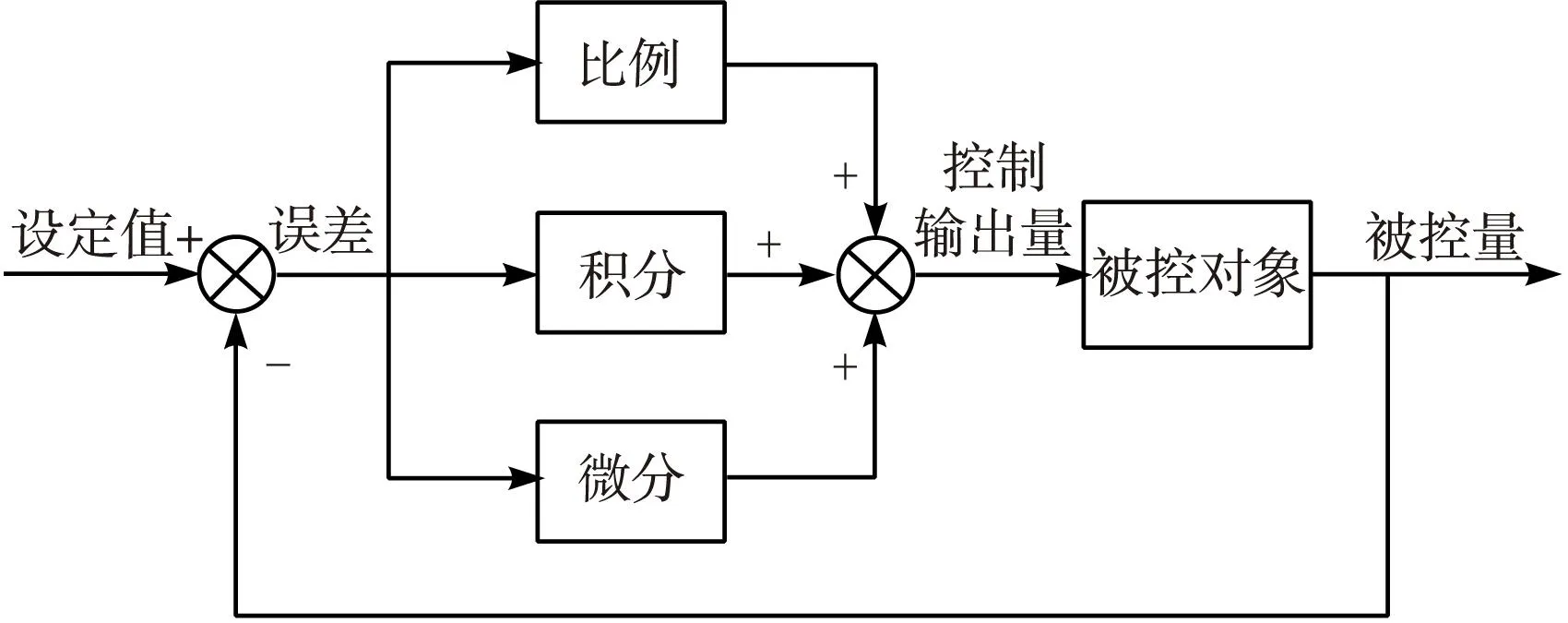
图1 PID控制结构原理图
2轨迹跟踪算法的分析
2.1PD控制
基于重力补偿的PD控制律为[5]
(2)
取跟踪误差为e=qr-q,考虑一个N关节的机械臂,其动态性能可由二阶非线性微分方程描述[6]:

(3)

(4)
整理为
(5)
取Lyapunnov(李雅普诺夫)函数为
(6)
则有
(7)
(8)

2.2PID控制
PID控制规律为[7]
(9)
考虑一个N关节的机械臂,其动态性能可由二阶非线性微分方程描述:
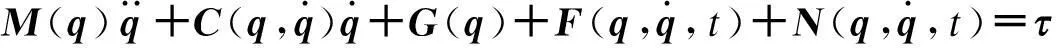
(10)

(1)假设对一定条件下α,所有的q∈Rn满足‖Γ(q)‖=‖In×n-M(q)-1M‖≤α<1。
(2)假设∂Ν(0,0,t)/∂t=0,从而φ(0,0,t)=M(0)-1∂N(0,0,t)/∂t=0,初始点是闭环系统状态方程的一个平衡点。模型误差估计量初始值为w(0)=v(0),模型误差函数的初始值e(0)包含于集合中We⊂Rn中。
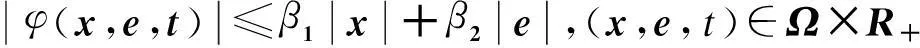
因此,存在εmax>0对所有的ε∈(0,εmax)满足使式子右边为负正定。
3仿真研究
本文的实验研究对象为两自由度的机械臂,为了便于比较分析,对PID控制中的摩擦力矩及能量损耗补偿予以忽略,使其具有相同的描述动态性能的二阶非线性微分方程。机械臂的动力学模型为
(11)
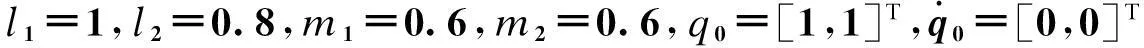
本文采用Matlab/Simulink建模与仿真[9],仿真模型及结果如图2~图3所示。

图2 PD控制仿真模型
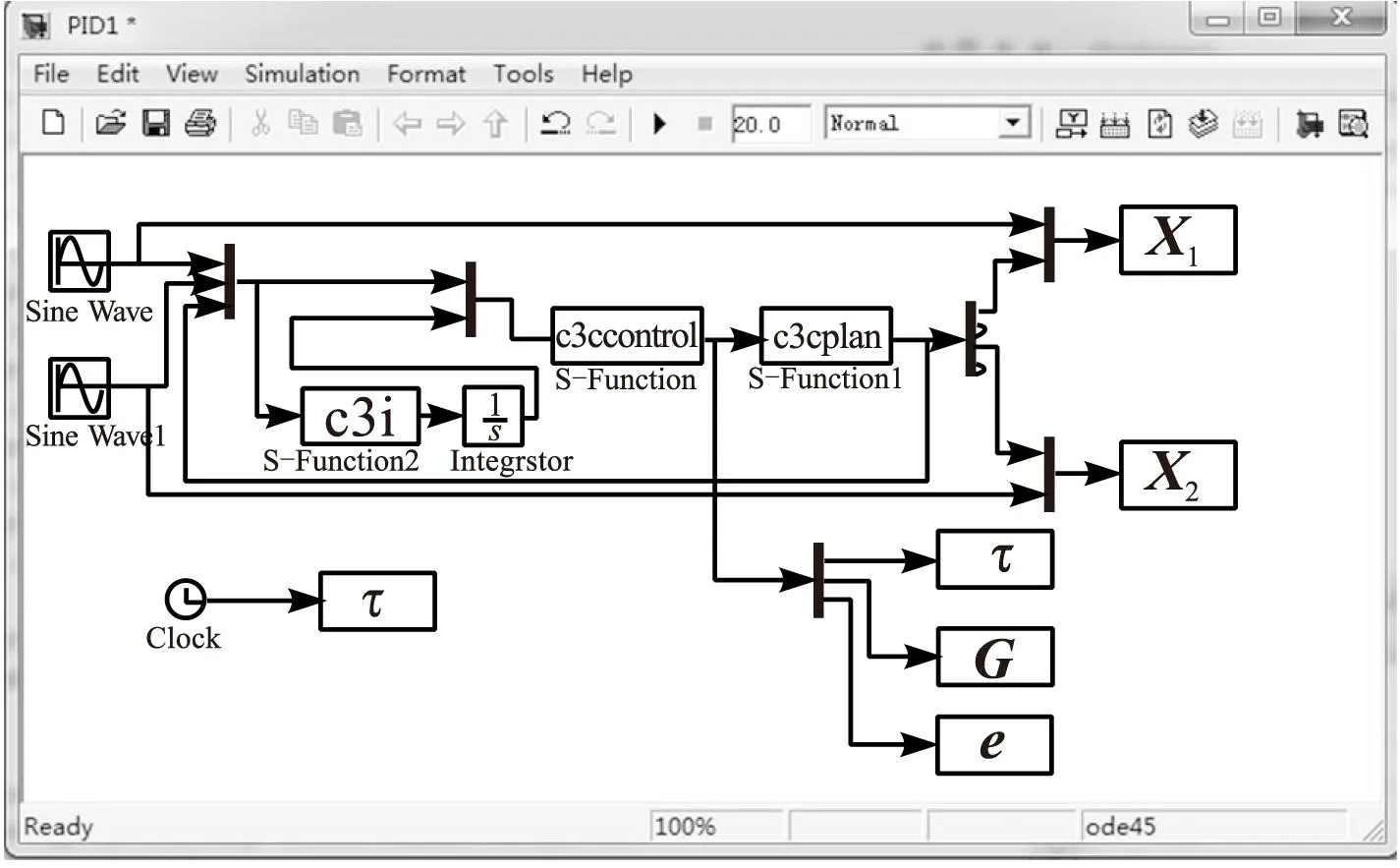
图3 PID控制仿真模型
PD控制仿真结果如图4~图7所示。从图中可以看出,PD控制算法能够实现机械臂的轨迹跟踪,跟踪效果一般。轨迹跟踪误差较大,关节1的误差最大达到0.14rad,关节2的误差最大达到0.12rad,并且误差波动比较大,响应速度较慢。
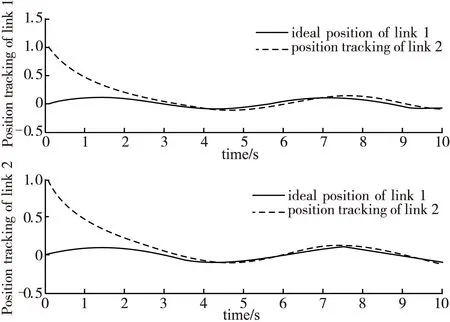
图4 PD控制轨迹跟踪曲线图
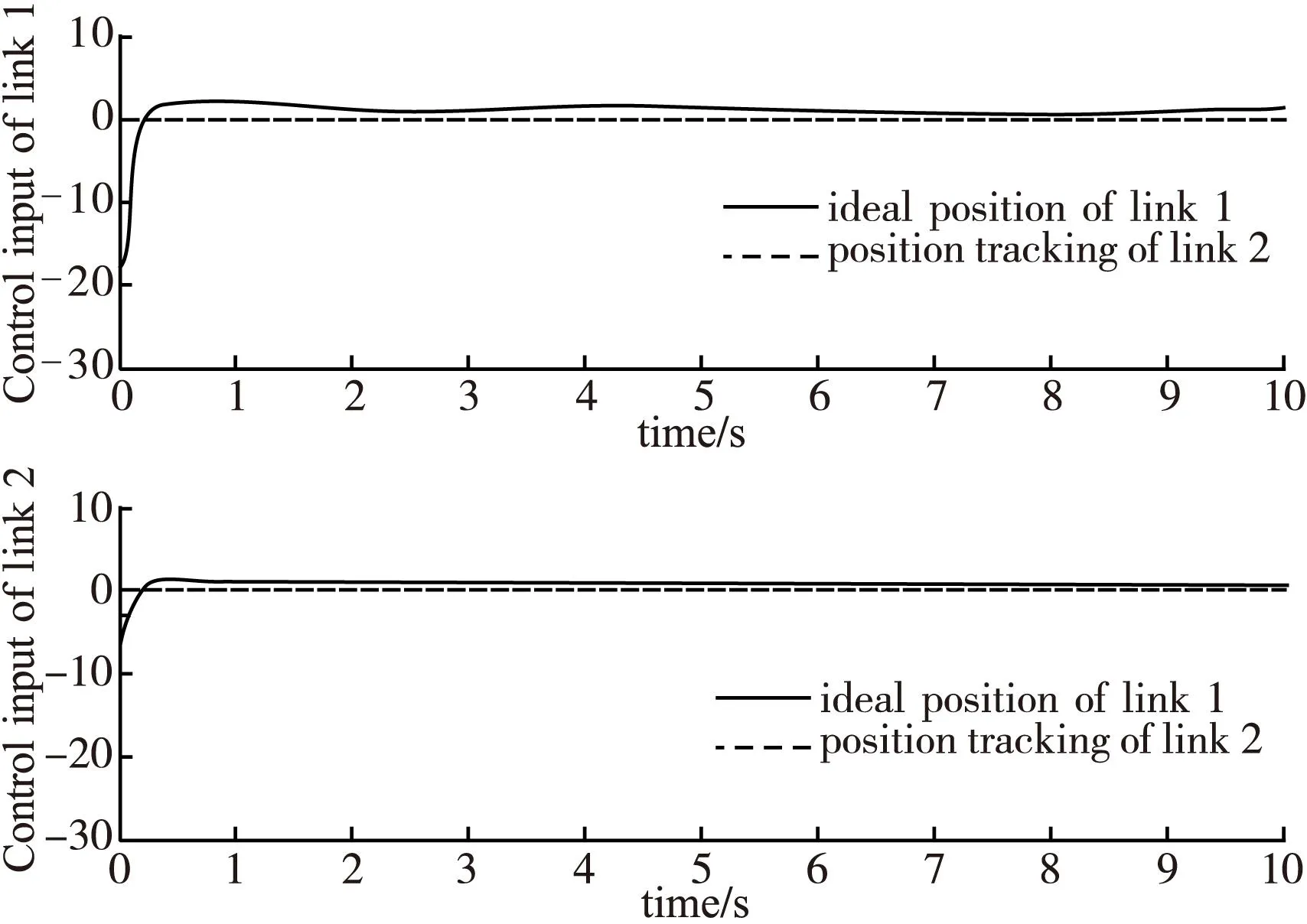
图5 PD控制力矩输入变化图

图6 PD控制轨迹跟踪误差图

图7 PD控制重力补偿图
PID控制仿真结果如图8~图11所示。从图中可以看出,相比较PD控制算法,PID控制算法轨迹跟踪效果较好。轨迹跟踪误差明显减小,关节1的误差最大达到0.05rad,关节2的误差最大0.04rad,并且误差波动比较小,响应速度有所提高。
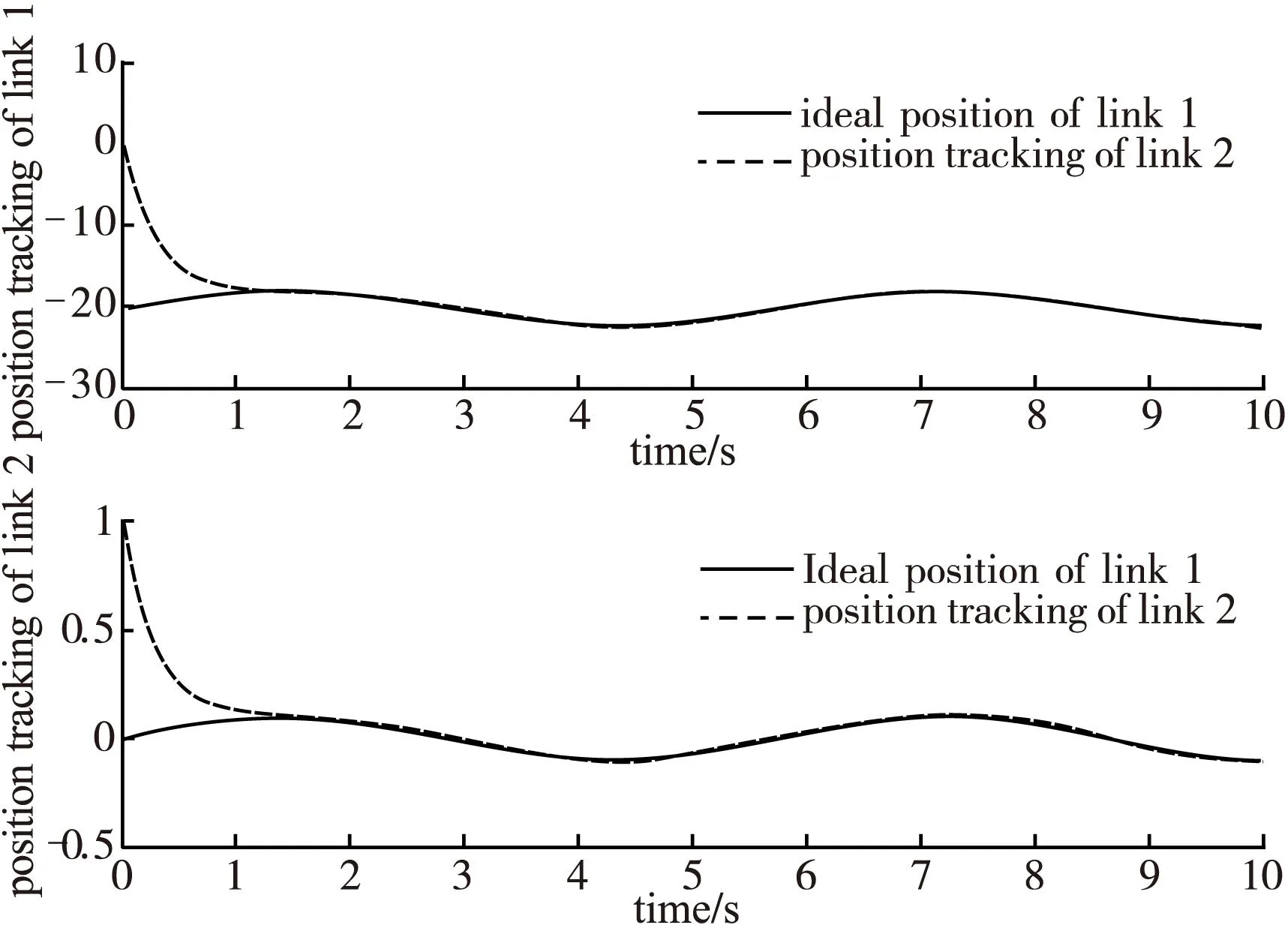
图8 PID控制轨迹跟踪曲线图

图9 PID控制力矩输入变化图

图10 PID控制轨迹跟踪误差图
通过对两种算法的实验结果对比分析,PD控制算法和PID控制算法的响应速度都比较快,随着轨迹的不断变化,由于重力等因素的影响,PD控制算法的误差明显变大。PID控制算法由于积分环节的作用,其轨迹跟踪的能力明显强于PD控制算法。但在仿真实验过程中,逐步增大KP,即:PID控制中的积分作用过大,容易造成控制系统的不稳定,所以要选择合适的积分参数。由于忽略摩擦力矩及外界的不确定因素的干扰,具有一定的局限性,但其能够满足一般的控制精度要求。

图11 PID控制重力补偿图
4结束语
在分析PD控制与PID控制算法稳定性的基础上,通过比较仿真分析可知,两种控制算法都具有比较好的跟踪轨迹控制性能,PD控制的误差相对较大,这说明积分环节对控制效果的影响是明显的。通过仿真验证,两种控制算法简单有效,能够满足隧道掘进后期维护中,喷涂机械臂的控制要求,也能够适应其它一些环境下机械臂的工作。
参考文献:
[1]C Canudas de Wit,B Sicilian,G Bastin.Theory of Robot Control [M].Berlin:Springer,1996.
[2]Ayca Gokhan A K,Galip Cansever.Fuzzy sliding mode controller with neural network for robot manipulators[C]//IEEE International Conference on Control,Automation,Robotics and Vision.Hanoi,Vietnam,2008:1556-1561.
[3]Saiful Akhyar,Sigeru Omatu.Neuromorphic self-tuning PID controller[J].IEEE Transactions on systems,1993,1(10):552-557.
[4]江道根.六自由度并联机器人RBF神经网络PID控制研究[D].镇江:江苏大学,2010.
[5]刘金琨.机器人控制系统的设计与Matlab仿真 [M].北京 :清华大学出版社,2008.
[6]陈启军,王月娟,陈辉堂.基于PD控制的机器人轨迹跟踪性能研究与比较[D].上海:同济大学,2003.
[7]Paolo Rocco.Stability of PID Control for Industrial Robot Arms[J].IEEE Transactions on robotics and automation,1996,12(4):606-614
[8]J A Ramirez,I Cervantes,R Kelly.PID Regulation of robot manipulators:stability andperformance[J].Systems & Control Letters,2000(41):73-83.
[9]张德丰.MATLAB/Simulink建模与仿真实例精讲[M].北京:机械工业出版社,2010.
(责任编辑:马金发)
Research of Manipulator Trajectory Tracking Based on Gravity Compensation
JIANG Jing,CAO Song,LI Hongda
(Shenyang Ligong University,Shenyang 110159,China)
Abstract:Aiming at the problem of accuracy control of spraying manipulator in the tunnel engineering,the control method of the mechanical arm PD and PID is studied by gravity compensation.Two kinds of manipulator trajectory tracking algorithm stability and convergence are analyzed:PD control algorithm based on gravity compensation is the global asymptotic stability,but PID control algorithm is semi globally asymptotically stable under some conditions.Computer simulation results show that,the maximum error of PD was 0.14rad,and the maximum error of PID was 0.05rad.These two algorithms can achieve accurate tracking of the trajectory of mechanical arm,which meets the requirement of the position control of mechanical arm and show the effectiveness of the control method.
Key words:the mechanical arm;PID control;gravity compensation;trajectory tracking
中图分类号:TP29
文献标志码:A
文章编号:1003-1251(2016)02-0005-05
作者简介:姜静(1973—),女,副教授,博士,研究方向:复杂系统的建模、优化、控制及仿真。
基金项目:国家自然科学基金资助项目(51207096);爆炸科学与技术国家重点实验室 (北京理工大学)开放基金资助项目(KFJJ13-6M);沈阳理工大学重点学科开放基金资助项目
收稿日期:2015-05-18
