窗口分数维的初至波自动拾取
2016-06-02刘欣,李环,王茹
刘 欣,李 环,王 茹
(沈阳理工大学 信息科学与工程学院,沈阳 110159)
窗口分数维的初至波自动拾取
刘欣,李环,王茹
(沈阳理工大学 信息科学与工程学院,沈阳 110159)
摘要:地震初至波的拾取技术对石油、矿物资源的开发有着重要作用,目前的拾取方法大都以振幅、频率、相位作为初至波的判断依据。通过对分形理论的研究,结合滑动窗口原理,提出了一种新型的初至波自动拾取方法,该方法把分数维这一概念引入到地震初至波拾取中,通过每个窗口内的曲线变化来反映局部数据的特征——分数维,再依据总体数据特征的变化趋势情况来判断初至波,并确定其到达时刻。实验结果证明该方法优于传统拾取方法,其运算速度快,抗干扰能力强。
关键词:初至波;分数维;拾取技术
在地震波的研究中,初至波作为其中一项重要参数,一直以来是研究的关键步骤,现在初至波被广泛应用于计算表层速度、地质构造、矿物开发、石油勘探等方面。目前,关于地震初至波的拾取已经有了许多方法,但是由于地震资料的迅速增大,计算量的加剧增大,这些传统方法已经不能满足现在日益增长的数据需求。一般来说,传统拾取初至波的方法大都是依据地震记录的振幅、频率、相位变化进行拾取[1],而应对现代的大量地震数据,其效率和精确度大大降低,并且容易受到环境和噪声的影响,所以如何对初至波进行精确的拾取就变得至关重要了。
基于提高初至波拾取的准确度和速度,并对分形理论中滑动窗口方法进行了研究,发现该方法是依据窗口内的特征函数变化来显示突变事物的存在,并通过窗口内特征函数来判断突变事物的类型,其代表为Divider检测方法和Hurst检测方法[2]。通过结合分形理论中滑动窗口方法,提出了一种窗口分数维方法进行初至波拾取,通过窗口中分数维的变化揭示初至波的到来,其拾取效果有极大提高。
1初至波拾取的分形原理
1.1分形维数
19世纪初期分形理论开始提出,Hausdorff等数学家开始研究分形理论,认为空间物体都应该有分形维数的;1977年,Mandelbort提出了分形几何理论,在此之前人们普遍认为维数只能是整数,例如直线是一维的、平面是二维的,而分形几何理论认为维数可以是任意实数,即物体可以是中间维数。其理论主要研究对象为不规则图形,即描述图形的复杂度,刻画图形的层次结构等[3-5]。对于分形图形来说,是具有精细的结构、不规则性、自相似性的一组特征集合。根据以上理论,具有该类特点的图形可用分数维来进行研究,那么对于地震记录的数据来说,把地震记录数据的曲线进行无量纲处理后,转变成为分形图形,就可以运用分形理论对其进行分析研究。并且,结合分形理论的滑动窗口方法发现[6],把初至波的到来作为突变因素,那么特征函数——分数维在地震初至波到来的前后是不相同的,这种突变就成为判断初至波的重要依据。
简单地说,维数是一个图形的特征量,当用单位长度线段来测量方形面积,发现测量结果无穷大,说明选择尺度太小;同样地,用单位面积的方形测量直线长度,发现测量结果为零,说明选择尺度太大。这说明,测量的结果与测量的尺度有着密切关系,对于尺度的太大和太小,需要一个介于一维与二维之间的一个维数来测量,这个维数就是分数维。对于地震采集数据曲线经过无量纲化处理后,得到一条分形曲线,该曲线比直线要复杂、比方形要简单,用分数维去测量,才能更准确地描述曲线特性。
在结合滑动窗口[7]方法时,地震数据曲线应用窗口分数维方法时应遵循以下几个原则:(1)处理后得到的分形曲线可以在不断缩小或放大的窗口中具有相似性;(2)在计算分形曲线的分数维时,同样窗口大小下的结果可能不完全相同,但所得趋势不变;(3)同一分形曲线,用不同窗口大小计算得到分数维,可能并不相同,但对判断初至波无影响。
1.2地震数据的分数维计算
在一条处理后的分形曲线上,采用长度为w的窗口来包含整条曲线上的每一个部分,当n个窗口包含了完整的曲线,那么认为其测量长度为L=nw(图1)。当改变窗口长度w大小时,发现窗口长度w与分形曲线长度L存在一定的指数关系,即
L=Kw1-D
(1)
式中:K为比例常数,D为分形曲线上的分数维。
在分形曲线上,首先确定窗口长度w,然后沿曲线轨迹逐个移动窗口w,直至窗口w移动过整个分形曲线。同时计算该分形曲线在窗口长度w内的分数维,将所得到的数据进行记录并绘制在x-y坐标中,观察其坐标点所构成的曲线趋势。若改变窗口长度的值,计算出的曲线不尽相同,窗口长度w越小,其计算精度越高,但计算时间变长,基于综合计算时间和计算精度的原则,一般选取窗口长度w为采样间隔的整数倍。然后将所得数据代入式(1),经过对数运算,可得下式:
logL=(1-D)logw+lnK
(2)
根据分形理论可得,通过窗口长度w内的分数维变化,体现出分形曲线的局部特性,即地震数据曲线的变化情况,其分数维的突变反映出初至波到来时的数据突变。对所确定的突变点进行分析,系统会根据突变点与时间的对应关系自动计算出初至波的到达时刻[8]。

图1 地震道分数维的计算方法示意图
2初至波到达前后的分数维变化趋势
在地震初至波到达之前,其数据主要记录的是随机噪声,振幅相对较低;当初至波到达后,其记录的是噪声与初至波的叠加,振幅相对较大。这样,前后的分数维就会不同,发生明显的突变,其分数维的突变点标志了初至波的到达。该突变点对应时刻即为初至波到达时刻。图2为某地震数据曲线;图3为分数维趋势曲线,其中图中数字显示经过系统计算之后的突变点所对应时刻。由图2和图3可以看出,当初至波到达的前后,图2中的振幅和图3中的曲线趋势发生了变化,其图3曲线的变化趋势更明显、准确地反映出初至波到达,并根据其突变点自动计算出所对应的时刻,由此可见,采用窗口分数维方法判断地震初至波到达的时刻更为便捷、精确。

图2 某地震数据记录曲线
分数维是描述分形图形不规则性,在地震数据进行无量纲处理后,就属于分形图形,所以可以对其进行分数维运算。通过上述的理论知识分析,分数维的计算与地震数据的振幅、频率、相位没有任何关系,脱离了传统拾取方法的束缚。同时,窗口分数维方法不对初至波的类别进行规定,又克服了传统方法中单一性质的依赖,见图3。同时对曲线趋势的突变点进行标记,并自动计算出突变时刻,确定初至波到达时刻。

图3 某地震分数维趋势曲线
3实验方法与分析
在实验研究时,采用户外记录的原始数据作为实验数据,其采样频率为2048Hz,其中,图4、图5窗口长度为8倍采样间隔,图6、图7窗口长度为18倍采样间隔,截取其中一段关键数据(见表1),其中原始数据中混杂着大量工业噪声。在实验计算中,改变其窗口长度大小,多次计算不同窗口长度下的分数维,观察其选定窗口长度大小对分数维的影响,再结合分数维的变化趋势情况拾取初至波,验证该方法的可行性。

表1 截取实验数据
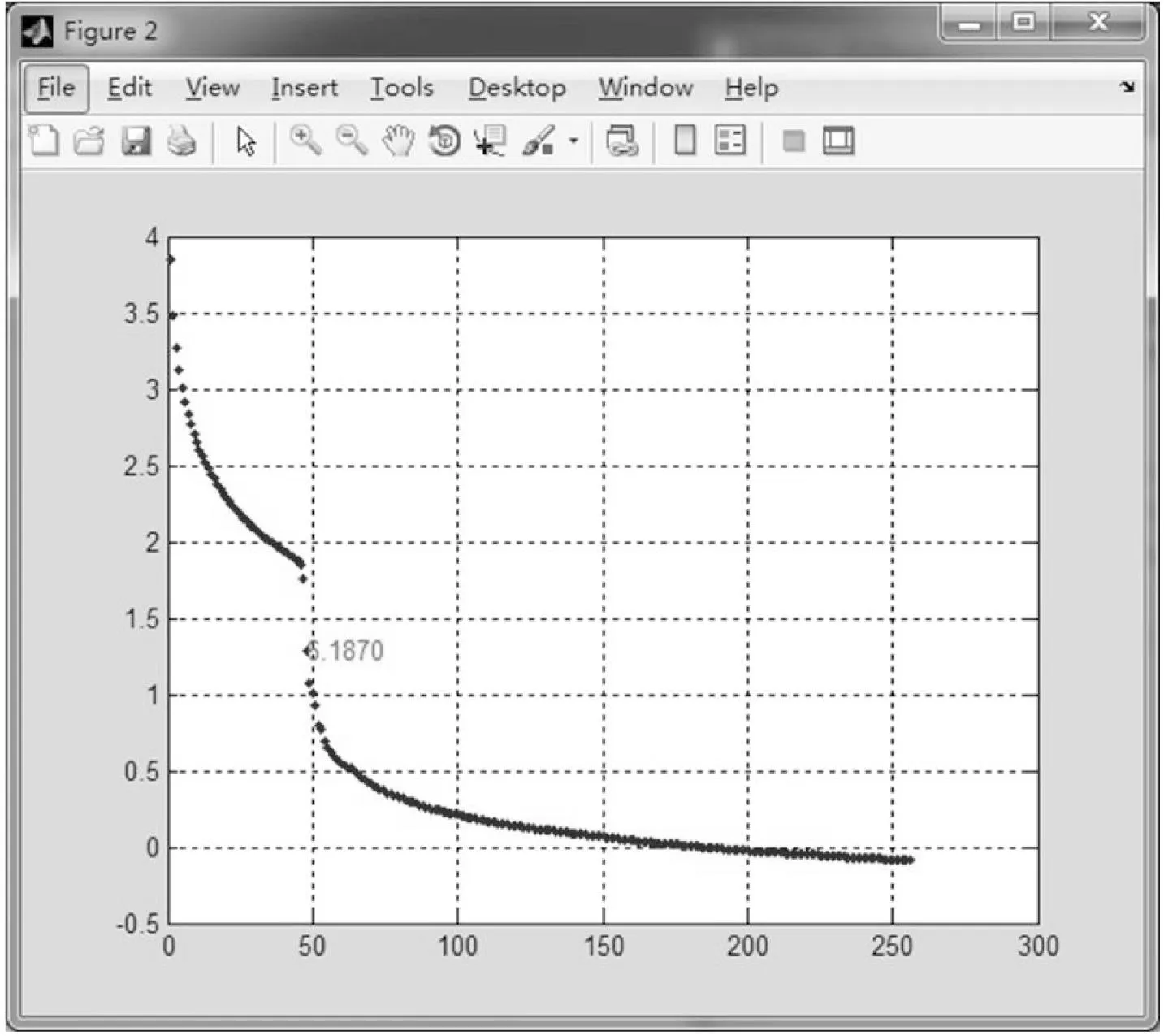
图4 窗口长度为8、信噪比为2分数维趋势曲线

图5 窗口长度为8、信噪比为4分数维趋势曲线

窗口序号趋势曲线分数维窗口序号趋势曲线分数维431.86800.0114481.62590.6136441.85660.0123491.01230.2404451.84430.0117500.77190.0785461.83260.0338510.69340.0794471.79880.1729520.61400.1374

图6 窗口长度为18、信噪比为2分数维趋势曲线

图7 窗口长度为18、信噪比为4分数维趋势曲线
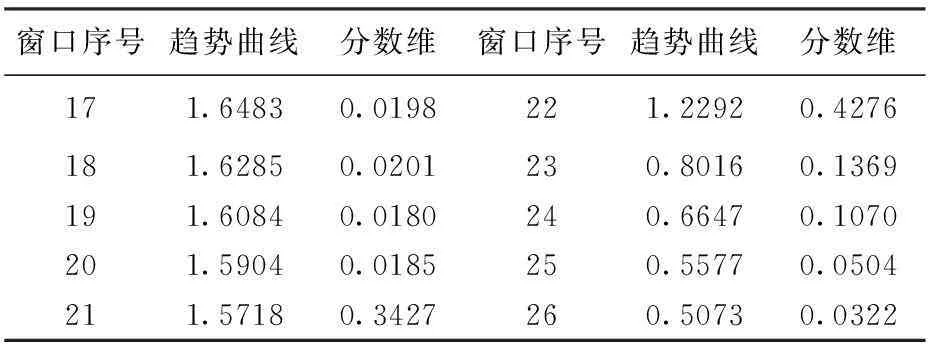
窗口序号趋势曲线分数维窗口序号趋势曲线分数维171.64830.0198221.22920.4276181.62850.0201230.80160.1369191.60840.0180240.66470.1070201.59040.0185250.55770.0504211.57180.3427260.50730.0322
从以上分析和实验可得出以下结论:(1)图4、图5和图6、图7明确看出,在初至波到来的前后时刻,曲线趋势发生明显变化,对应其分数维也发生明显变化。该趋势突变点标志了初至波的到达,说明采用窗口分数维方法可以判断初至波的到达时刻。(2)图4和图6比较可看出,在改变窗口大小时,仍能准确反映出曲线的变化趋势,即分数维的变化。(3)单独比较图4、图5和图6、图7可知,改变信噪比会使信号的幅值发生明显变化,但不会改变其分数维趋势曲线的走势,所得曲线趋势的突变点依然非常明显。
4结论
(1)分数维是刻画分形图形不规则程度和自相似程度,其特点不能用传统几何描述,但对数据曲线进行无量纲处理后,可以利用分数维的变化趋势来拾取初至波。
(2)采用窗口分数维的方法进行初至波拾取过程中并不依赖于振幅、频率、相位等要素,改变信噪比,并不影响分数维趋势曲线,因此该方法受干扰程度较小,与传统方法相比有了较大提高。
(3)采用窗口分数维的方法可以很直观、便捷、准确地确定突变点的位置,并根据突变点的位置,系统自动确定初至波的到达时刻,减少了不必要的运算量。
(4)在计算窗口内分数维时,缩小窗口大小可有效提高精确度,而增大窗口大小时,减少滑动窗口个数,大大减少其计算量,而曲线变化趋势基本无影响。
参考文献:
[1]曾福英.地震波初值拾取的分形研究[J].现代地质,2002,16(2):209-213.
[2] 周基阳.基于信息量的地震波动初至拾取[D].北京:华北电力大学,2011.
[3]孙洪军.分形理论的产生及其应用[J].辽宁工学院学报,2005,25(2):113-117.
[4]王建华.地震波初至自动拾取算法研究及三分量测井系统软件设计[D].长沙:中南大学,2007.
[5]杨俊峰.浅地层下震源信号初至波方法研究[D].太原:中北大学,2013.
[6]杨振,杨建强.石油勘探中地震波的分数维属性分析[J].中国石油和化工标准与质量,2014(9):162-164.
[7]程仲平,陈鹰鹏,何超群.空变时窗约束地震波初至的拾取方法[J].地球物理学进展,2011(5):1626-1631.
[8]王彩霞.多震相初值自动检测识别方法技术[D].西安:长安大学,2014.
(责任编辑:马金发)
Automatic Picking Preliminary Wave Based on Fractal Dimension
LIU Xin,LI Huan,WANG Ru
(Shenyang Ligong University ,Shenyang 110159 ,China)
Abstract:Preliminary wave picking technology plays an important role in the development of oil and mineral resources,the current methods of picking technology mostly in the amplitude and frequency and phase are taken as the major judgment for preliminary wave.Through the principles studying of fractal theory,a new kind of primary wave automatic picking method is proposed by sliding window,and the concept of the fractal dimension is introduced into this method to the preliminary wave picking,by each window reflecting the characteristics of the datafractal dimension,and then according to fractal dimension changing of picking primary wave,the arrival time of primary wave is determined.Experimental results show that the proposed method is superior to traditional picking methods,which has good operation speed,strong interference capability.
Key words:preliminary wave;fractal dimension;picking technology
中图分类号:TP391
文献标志码:A
文章编号:1003-1251(2016)02-0035-04
作者简介:刘欣(1990—),男,硕士研究生;通讯作者:李环(1964—),女,教授,研究方向:扩频通信技术及应用等。
基金项目:辽宁省自然科学基金资助项目(2015020028)
收稿日期:2015-03-26
