几种运动轨迹的数学表达式
——基于物体所受合外力与其初速度夹角的分析
2016-06-01郭子坤郭柏寿
◎郭子坤 郭柏寿
(1.西北农林科技大学附属中学,陕西 杨凌 712100;2.西北农林科技大学,陕西 杨凌 712100)
几种运动轨迹的数学表达式
——基于物体所受合外力与其初速度夹角的分析
◎郭子坤1郭柏寿2
(1.西北农林科技大学附属中学,陕西 杨凌 712100;2.西北农林科技大学,陕西 杨凌 712100)

采用数学分析的方法,求解上述5种运动轨迹的数学表达式,证明其轨迹的几何形态,仅做借鉴,以增强高中阶段学生对物理问题进行数学推导和演绎的意识.
一、合外力F和初速度v0夹角θ=0
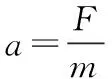
显然,上面方程组定义的运动轨迹为与x轴重合的直线,为匀加速直线运动,当F=0时为匀速直线运动,此为匀加速直线运动的特殊情况.

图1 v0与F夹角θ=0
二、合外力F和初速度v0夹角θ=π
当F和v0矢量夹角θ=π时,它们位于同一条直线上且方向相反,以其所在的直线作为x轴,起点为原点O,建立平面直角坐标系(见图2).v0在x轴上的分量为vx=v0cosθ=v0cosπ=-v0,v0在y轴的分量为vy=v0sinθ=v0sinπ=0.根据牛顿第一和第二定律可知,该物体t时于x轴和y轴上的位移由下面的联立方程决定:
上述方程组定义的运动轨迹显然为与x轴重合的直线,该物体先做初速度为v0的匀减速直线运动,当速度减至0时,将沿合外力F方向做初速度为0的匀加速直线运动.
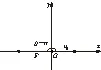
图2 v0与F夹角为θ=π
三、合外力F和初速度v0夹角
以物体运动起点为原点O,v0所在的直线为x轴(规定沿v0方向为x轴正方向),合外力F所在的直线为y轴(规定沿F方向为y轴的正方向),见图3.
由图3可知,物体在x轴方向所受的力为0,根据牛顿第一运动定律,在x轴方向没有力来改变该方向的运动状态,所以物体在x轴的分运动为初速度等于v0的匀速直线运动,时刻t时,在x轴方向的位移为:x=v0t.
①
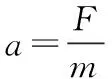
②
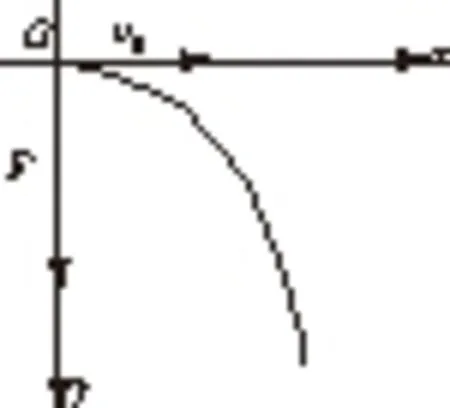
图3 v0与F夹角为

③

四、合外力F和初速度v0夹角
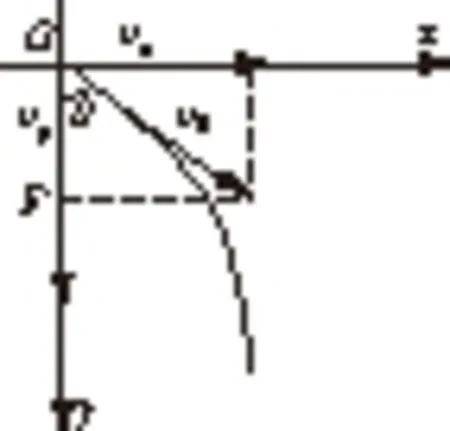
图4 F与v0夹角
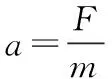

⑥
五、合外力F和初速度v0夹角<θ<π
同样,以物体运动起点为原点O,F所在直线为y轴,F方向为y轴正方向;以垂直于y轴的直线为x轴,将x与v0呈锐角的方向定为x轴正方向,如图5所示.

图5 F与v0夹角
⑦
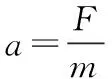
⑧
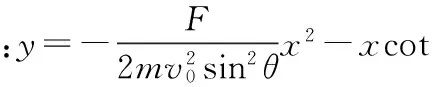
⑨
