基本不等式求最值中“定值”的必要性
2016-06-01周国明
数学学习与研究 2016年24期
◎周国明
(唐山一中,河北 唐山 063000)
基本不等式求最值中“定值”的必要性
◎周国明
(唐山一中,河北 唐山 063000)
在高中数学必修五中,关于基本不等式的应用,我们常说“和定等积大,积定等和小”,也就是:两个正数,若“和”为定值,则在它们相等的时候“积”取得最大值;若“积”为定值,则在它们相等的时候“和”取得最小值.
基本不等式;求最值;求最值中“定值”
很多同学对“定值”的理解是不够深刻的,他们会有疑问:“积”如果不是定值,而是有范围的,为什么求“和”的最小值时就不能用基本不等式?针对这个问题,我在本文中通过两道例题,做深入透彻的说明.

(1)求xy最小值.
(2)求x+y最小值.
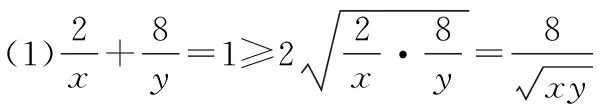
①

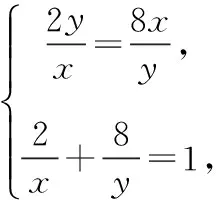
②
这个方法对吗?
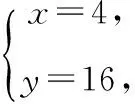
由题干,显然x+y可以统一为只有一个变量x的函数,记为f(x);


为了理解更为深刻,我们再看例2.
例2 若a>0,b>0,满足ab=a+b+3.
(1)求ab范围.
(2)求a+b范围.

t2-2t-3≥0,即t≥3,故ab≥9,

③
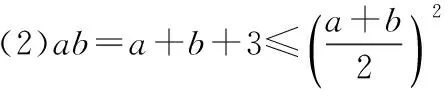
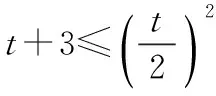
④
结果是一样的.为什么呢?④式中,两个等号同时成立,需要③即可.
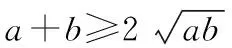
通过以上两题,希望能帮助大家理解“和定等积大,积定等和小”.基本不等式求最值,一定要注意“定值”的意义,一般情况下,关于两个正数的“和”与“积”,我们要已知其中一个是定值,才能求另一个的范围.
