遥感卫星双相机组合成像偏流角修正残差分析

朱兴鸿 韩杏子

（1国防科技大学航天科学与工程学院，长沙 410073）（2航天东方红卫星有限公司，北京 100094）

遥感卫星双相机组合成像偏流角修正残差分析

朱兴鸿1，2韩杏子2

（1国防科技大学航天科学与工程学院，长沙 410073）（2航天东方红卫星有限公司，北京 100094）

针对国内遥感卫星工程中使用的双相机组合成像的配置，分析了双相机组合成像在偏流角修正中可能引入的误差，提出了一种通用的几何分析模型。基于全视场成像仿真方法，结合卫星实际场景，对卫星在不同姿态机动状态下的模型有效性进行了验证。研究结果表明：使用双相机组合成像的卫星，在无姿态机动（星下点成像）或常规侧摆机动时，成像质量基本不受影响；而俯仰机动时，系统将存在较大的偏流角修正残差，因此设计双相机组合成像卫星时不建议采用大角度俯仰机动成像。

遥感卫星；双相机组合成像；时间延迟积分CCD；成像质量；偏流角；残差

1 引言

近年来，航天遥感技术的发展对遥感卫星的重访性能和图像获取能力提出了更高的要求，但在星上相机的设计中，受制于时间延迟积分CCD（TDICCD）器件的尺寸和像元特性，以及长焦相机宽视场设计的复杂度等多方面的因素，国内的一些高分辨率遥感卫星配置了2台相同的相机，以双相机同时成像结合视场拼接的方式来提高相机的幅宽和重访性能，其中典型的有我国高分一号卫星［1］和“委内瑞拉遥感卫星”［2］，本文将此种视场拼接成像的方式称为双相机组合成像。

TDICCD相机在卫星线阵方向的成像过程控制是通过偏流角控制实现的，即通过调整卫星的偏航姿态，使物像速度在TDICCD焦平面的分量方向完全垂直于修正后的TDICCD线阵方向，从而消除焦平面的横向像移［3］。TDICCD的延时积分功能可利用多级敏感单元对运动的同一个目标进行多次积分，使相机的信噪比、动态范围等性能得到有效改善［45］，但多级积分的工作方式也会成倍放大引起成像质量下降的各种因素的影响，如CCD线阵方向的像移［6］。在双相机组合成像中，为了实现视场拼接，2台相机的焦平面无法处于同一个平面内，使成像过程中的偏流角修正控制需求也会存在一定的差异，而这种差异在之前的研究中均未考虑［7－9］，从而可能导致未预见的成像质量下降。因此，基于双相机组合成像的偏流角控制策略，对相机在轨的偏流角修正残差造成的影响进行研究，具有重要的工程价值。为此，本文将重点讨论以下3个方面的问题。

（1）从成像的物理特性出发，对双相机在轨的偏流角修正残差建立几何分析模型，研究影响双相机组合成像的偏流角修正残差的关键要素。

（2）结合全视场成像仿真方法［3］，对双相机在不同成像姿态下的全视场偏流角修正残差进行仿真，验证几何分析模型的结果，并解决几何分析模型对全视场成像条件差异性考虑不足的问题。

（3）结合分析数据，对双相机组合成像卫星的使用给出工程实施的建议。

2 双相机组合成像偏流角修正残差的几何分析模型

2．1 双相机组合成像几何特性

双相机组合成像几何特性见图1，图中所示为飞行过程的二维切面，飞行方向为垂直于纸面方向朝里。

从图1中可以看出，配置2台相机使垂直于卫星飞行方向的地面成像幅宽得到成倍增加。常规设计中，为了能够实现双相机视场的无缝拼接，会保留一定的视场覆盖重叠区，之后通过重叠覆盖图像匹配等方式进行双相机的图像融合拼接。在工程中，为了降低系统设计难度，一般使用2台完全相同的相机，并采用组合安装的方式控制2台相机的光轴夹角，从而保证2台相机的组合视场及视场重叠。

2．2 双相机组合成像偏流角控制问题

卫星对沿TDICCD方向的横向像移控制，是利用卫星的偏流角修正实现的，修正的目的是通过卫星的姿态调整，将TDICCD的线阵方向修正到完全垂直于成像点相对于TDICCD的运动速度，消除TDICCD的横向像移，从而维持成像过程中TDICCD相对于地面场景位相的稳定性［10］。

由于偏流角修正过程中的像移控制是在TDICCD焦平面上定义的，因此成像点相对于TDICCD的运动速度要先在焦平面内进行投影，然后才能通过投影矢量与CCD线阵间的关系得到偏流角修正，如图2所示。图2中，Va为成像点相对于卫星的运动速度，NCCD为TDICCD的法线方向，VaPJ为Va在CCD焦平面上的投影，修正的目的是使NCCD与VaPJ重合。

双相机组合成像卫星与单相机卫星的偏流角控制存在一定的差异，如图3所示。在单相机卫星上，使用姿态控制分系统进行偏流角修正时，可以取单相机焦平面为偏流角控制平面，在一个平面内可以直接将图2中的NCCD与VaPJ修正到重合，完全消除CCD焦平面上的横向像移。在双相机组合成像卫星上，对2台相机采用光轴夹角进行组合安装时，会造成2台相机的焦平面处于非共面的状态，因此，在利用2台相机的CCD焦平面通过投影计算各自的偏流角修正值时，将会得到不同的结果。卫星在通过姿态修正偏流角时，必须选定一个偏流角的控制平面，因此，整星的偏流角修正无法同时保证2台相机在CCD焦平面上没有横向像移。为了保证2台相机的成像质量相近，在实际修正偏流角的过程中，只能进行折中处理，将光轴角平分线假想为组合相机的光轴，将垂直于光轴角平分线的平面假想为组合相机的焦平面，进而选择此假想焦平面为卫星的偏流角控制平面（一般为卫星本体坐标系的XOY平面）。

图3 单相机卫星和双相机组合成像卫星的偏流角控制差异Fig．3 Different drift angle control approaches between single－camera and dual－camera combined imaging satellites

2．3 偏流角修正残差的几何分析模型

在双相机组合成像卫星中，偏流角修正参考平面是一个假想焦平面，定义此假想焦平面内的CCD法线方向为NREF，在卫星完成了偏流角修正后能够保证在假想焦平面内的VaPJ与NREF夹角为0。以相机A为例，可以建立如图4所示的几何关系，图中OP为Va（OM）在假想焦平面上的投影，OQ为Va在相机A焦平面上的投影。可以看出：相机A的CCD法线方向NCCD－A与NREF方向重合，由于相机A焦平面与偏流角控制平面不同，完成修正后Va在相机A焦平面上的投影矢量VaPJ－A与相机A的CCD法线方向NCCD－A存在一定的夹角β（∠POQ），即为在相机A焦平面上的偏流角修正残差。

图4中定义了以下2个角度。

（1）α为成像点相对于卫星的运动速度Va与偏流角修正平面的夹角。由于VaPJ为Va在偏流角修正平面的投影，α即为图中的∠MOP。

（2）δ为Va与VaPJ形成的平面与相机A焦平面所成二面角的平面角，即为相机A焦平面与偏流角修正平面夹角的余角，在图中为∠MPQ。

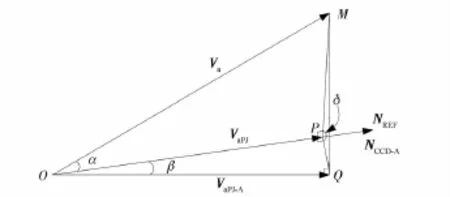
图4 双相机组合成像卫星的偏流角修正误差矢量图（相机A）Fig．4 Drift angle residual error vectorgraph of a dual－camera combined imaging satellite（camera A）

根据图4可以建立如下关系。

对于相机B的计算过程来说，与相机A完全相同，如果定义相机A的偏流角修正残差为正，则相机B的修正残差为负。从式（2）可以看出，对于偏流角修正残差β的影响因素只有α和δ，其中δ是设计决定的，而α则与卫星的成像状态相关，下面对不同姿态下的残差影响进行趋势性分析。

2．4 基于几何分析模型的偏流角修正残差分析

利用式（2），对不同姿态下成像的偏流角修正残差进行分析。为了得到一个趋势性的分析结论，这里假设卫星的轨道为倾角90°的圆轨道（实际选择的太阳同步轨道大多接近此值），并且参照上面的分析，取卫星本体坐标系的XOY平面为偏流角修正参考平面。在无姿态机动、侧摆机动和俯仰机动3种状态下，参考平面与地面成像点的运动几何关系示意如图5所示，Va分解为因卫星运动而产生的成像点运动速度VS和成像点由于地球自转产生的速度VE的矢量和。

进而可得

1）无姿态机动

在图5（a）中，Va与卫星本体坐标系XOY平面的夹角α很小，所以，从式（2）可以得到偏流角修正残差β近似等于0。VS与VE均处于XOY平面内，因此VE的大小对β几乎无影响，无论处于高纬度地区还是赤道，偏流角修正残差维持不变。

2）侧摆机动

在图5（b）中，VS仍然处于XOY平面内，但VE不在此平面内，导致α不为0。由于VE和VS相比为小量，因此总体来说，侧摆机动对β的影响较小。α随着VE的增大而增大，在赤道位置的β将达到最大值；随着纬度增大，β将逐渐减小；在接近极区时，VE可以忽略，α近似为0，β也近似为0。

3）俯仰机动

在图5（c）中，卫星俯仰机动时，Va与XOY平面的夹角α近似等于卫星俯仰机动的角度，因此从式（2）中可以看出，在α不为0时，β将随之增大。如果取俯仰角为30°，相机按照偏离星下点2°计算，当卫星轨道高度为650km时，α为33．4°，此时的β为1．32°。对于使用TDICCD的相机来说，此残差将造成一定的横向像移，在积分级数较大时将严重影响其垂直轨道方向的成像质量［11］。

以上是基于2台相机的视轴进行的几何建模分析，而在实际工程中，相机视场的差异会导致成像条件的不同，因此下文将逐步通过建模和仿真对几何分析模型进行验证，进而基于全视场成像仿真对双相机组合成像的偏流角修正残差及其影响进行分析。

3 仿真验证与分析

3．1 仿真验证过程

本文利用文献［3］中的全视场成像仿真方法验证几何分析模型的正确性，仿真分析过程如图6所示。仿真中重点考虑全视场内的成像质量差异问题，根据偏流角的仿真分析结果，通过控制卫星姿态的方式对偏流角进行严格修正［12］。由于姿态控制精度有限而造成的偏流角修正偏差等因素，均不在本文的分析范围内。

图6 仿真交互及分析过程Fig．6 Process of simulation interaction and analysis

3．2 双相机组合成像卫星场景仿真

仿真场景中选取光学遥感卫星常用的太阳同步轨道，高度为650km，降交点地方时为10：30，卫星场景见图7。

卫星上配置2台TDICCD相机，单台相机的视场设为4°，不考虑2台相机视场的微小重叠，2台相机的光轴夹角设为4°；2台相机的视轴分别垂直于各自的焦平面，偏流角控制平面与卫星本体坐标系的XOY平面重合。

3．3 侧摆机动仿真结果

针对上述仿真场景，以无姿态机动（星下点成像）和侧摆机动（10°，30°）为例，仿真获得2台相机全视场的偏流角修正残差随卫星纬度变化的关系如图8所示，仿真区间选取了一个完整的降轨成像过程。由于相机视场为4°，这里对每台相机均以全视场中的3个特征方向（2个视场边缘和视场中央）为代表来表征全视场的状态。从图8中可以看出，视轴位置（视场为0°）的仿真结果曲线和几何分析模型所得到的结论是一致的：在无侧摆机动时，残差很小；在有侧摆机动时，极区附近的残差近似为0，在赤道位置达到最大，并且在2台相机上造成的成像残差方向是相反的。

3．4 俯仰机动仿真结果

使用相同的仿真场景和仿真区间，以10°，20°，30°的俯仰机动为例，仿真获得2台相机全视场的偏流角修正残差随卫星纬度变化的关系如图9所示。从图9中可以看出：仿真结果与几何分析模型的非常吻合，在俯仰30°机动时，视轴方向上偏流角修正残差大小为1．315°～1．325°，几何分析模型得到的结果为1．320°。

图9 俯仰机动全视场偏流角修正残差仿真分析结果Fig．9 Analysis results of full－view drift angle residual error for pitching maneuver simulation

3．5 结果分析

通过全视场仿真结果可以看出，本文提出的几何分析模型是有效的。结合仿真结果可知，即使在侧摆30°机动时，2台相机的偏流角修正残差也不大于0．080°。对于TDICCD来说，即使积分级数取到48级，调制传递函数（MTF）的衰减系数也仅为0．998［13］，在工程中其影响可以忽略。在俯仰机动中，双相机组合成像会引入较大的偏流角修正残差。例如：在俯仰30°机动时，其视场边缘的偏流角修正残差达到了1．330°，对于TDICCD，即使选用12级积分级数，MTF衰减系数也已经达到了0．968；当使用24级和48级成像时，MTF衰减系数分别达到0．877和0．562，对在轨成像质量来说难以接受。

结合几何分析模型和全视场仿真分析结果可以看出，双相机组合成像适用于不具有姿态机动能力的卫星或者仅具有侧摆机动能力的卫星，此时成像过程的偏流角修正残差处于工程可接受的水平。针对具有俯仰机动能力的卫星，提出如下建议。

（1）在星上应避免采用双相机组合成像的方式。

（2）如果采用双相机组合成像的方式，且必须在俯仰机动时成像，则要求俯仰角尽可能小。在前文仿真场景中，卫星俯仰10°机动时，对于24级和48级积分级数，MTF衰减系数分别为0．989和0．956。

（3）如果要在大角度俯仰机动时成像，则可以通过牺牲相机B的图像质量来换取相机A的图像质量。具体来说，在对卫星进行偏流角修正时，选取相机A焦平面为偏流角修正平面，保证相机A可以消除偏流角修正残差，但此时相机B的偏流角修正残差会成倍增加，图像质量退化更加严重。

4 结束语

本文对遥感卫星双相机组合成像几何特性，以及卫星在轨进行偏流角修正过程中存在的问题进行分析，提出了几何分析模型，并利用全视场成像仿真方法进行验证，结合卫星场景给出了双相机在不同姿态下的全视场偏流角修正残差分析结果以及相关的工程建议。在本文的几何分析模型和仿真场景中，没有考虑相机前视安装等情况，因此后续将结合工程中相机的不同安装方式进行差异化几何建模，并结合全视场成像仿真方法全面获取各种双相机组合成像情况对成像质量的影响。通过细化几何分析模型，可以在卫星总体任务分析阶段得到与实际卫星状态更接近的系统分析结果，从而实现更为准确的相机成像质量预估。

（

）

［1］白照广．高分一号卫星的技术特点［J］．中国航天，2013（8）：5－9 Bai Zhaoguang．Technical characteristics of GF－1satellite［J］．Aerospace China，2013（8）：5－9（in Chinese）

［2］赵键，崔玉福，赵鸿志．委内瑞拉遥感卫星－1项目及典型应用介绍［J］．国际太空，2014（12）：28－33 Zhao Jian，Cui Yufu，Zhao Hongzhi．Introduction to Venezuela remote sensing satellite－1project and its typical applications［J］．Space International，2014（12）：28－33（in Chinese）

［3］朱兴鸿，王瑞，白照广．遥感卫星全视场成像质量仿真方法研究［J］．航天器工程，2013，22（6）：11－17 Zhu Xinghong，Wang Rui，Bai Zhaoguang．Simulation method analysis on full－view imaging quality for remote sensing satellite［J］．Spacecraft Engineering，2013，22（6）：11－17（in Chinese）

［4］Wong H，Yao Y，Schlig E．TDI charge coupled devices：design and applications［J］IBM Journal of Research and Development，1992，36（1）：83－104

［5］樊超，李英才，易红伟．速高比对TDICCD相机的影响分析［J］．兵工学报，2007，28（7）：817－821 Fan Chao，Li Yingcai，Yi Hongwei．Influence of velocityheight ratio of satellite on the TDICCD camera［J］．Acta Armamentarii，2007，28（7）：817－821（in Chinese）

［6］Wu Jiagu，Zheng Zhenzhen，Feng Huajun，et al．Restoration of TDI camera images with motion distortion and blur［J］．Optics and Laser Technology，2010，42（8）：1198－1203

［7］袁孝康．星载TDI－CCD推扫相机的偏流角计算与补偿［J］．上海航天，2006，23（6）：10－13 Yuan Xiaokang．Calculation and compensation for the deviant angle of satellite borne TDI－CCD push scan camera［J］．Aerospace Shanghai，2006，23（6）：10－13（in Chinese）

［8］樊超，李英才，易红伟．空间相机中的偏流角分析［J］．红外与激光工程，2006，35（10）：216－220 Fan Chao，Li Yingcai，Yi Hongwei．Analysis of drift angle on space camera［J］．Infrared and Laser Engineering，2006，35（10）：216－220（in Chinese）

［9］陈绍龙．侧摆摄影偏流角和速高比的计算模型［J］．航天器工程，2010，19（1）：36－40 Chen Shaolong．Computation model of veer angle and velocity－height ratio for space camera in roll attitude［J］．Spacecraft Engineering，2010，19（1）：36－40（in Chinese）

［10］李友一．空间相机中的偏流角控制［J］．光学精密工程，2002，10（4）：402－406 Li Youyi．Drift angle control for space cameras［J］．Optics and Precision Engineering，2002，10（4）：402－406（in Chinese）

［11］杨秀彬，贺小军，张刘．偏流角误差对TDI CCD相机成像的影响与仿真［J］．光电工程，2008，35（11）：45－50 Yang Xiubin，He Xiaojun，Zhang Liu．Effect and simulation of the deviant angle error on TDI CCD cameras image［J］．Opto－Electronic Engineering，2008，35（11）：45－50（in Chinese）

［12］朱兴鸿，邸国栋，陆春玲．一种遥感卫星偏流角修正的仿真分析方法［J］．航天器工程，2013，22（1）：39－43 Zhu Xinghong，Di Guodong，Lu Chunling．Simulation method analysis on drift angle for remote sensing satellite［J］．Spacecraft Engineering，2013，22（1）：39－43（in Chinese）

［13］邸国栋，朱兴鸿．TDICCD相机安装精度对系统调制传递传函的影响［J］．航天器工程，2012，21（4）：59－62 Di Guodong，Zhu Xinghong．Analysis on system MTF degradation effects of assembly precision of TDICCD camera［J］．Spacecraft Engineering，2012，21（4）：59－62（in Chinese）

（编辑：夏光）

Analysis of Drift Angle Residual Errors for Dual－camera Combined Imaging in Remote Sensing Satellite

ZHU Xinghong1，2HAN Xingzi2
（1College of Aerospace Science and Engineering，National University of Defense Technology，Changsha 410073，China）（2DFH Satellite Co．，Ltd．，Beijing 100094，China）

Dual－camera combined imaging system is equipped in domestic remote sensing satellite projects．The possibly induced drift angle residual error of the combined imaging is studied and a geometrical analytical model is established．The model is validated based on the full－view simulation method under different attitude maneuver conditions according to actual satellite imaging scena－rios．The result shows that the dual－camera combined imaging has good performance during sub－satellite point imaging as well as rolling maneuver，but a big drift angle residual error is foreseen to be induced while imaging at big pitching angle maneuver．For this reason the big pitching angle maneuver imaging should not be adopted while designing dual－camera combined imaging satellites．

remote sensing satellite；dual－camera combined imaging；TDICCD；imaging quality；drift angle；residual error

V474．2；P236

A

10．3969/j．issn．1673－8748．2016．02．002

2015－07－23；

2015－10－27

国家重大航天工程

朱兴鸿，男，硕士，高级工程师，从事卫星总体设计工作。Email：little．zhuxh@gmail．com。