K频段测距系统星间高精度指向控制算法

辛宁 邱乐德 周钠 张立华

（1中国空间技术研究院通信卫星事业部，北京 100094）

（2航天东方红卫星有限公司，北京 100094）

K频段测距系统星间高精度指向控制算法

辛宁1邱乐德1周钠1张立华2

（1中国空间技术研究院通信卫星事业部，北京 100094）

（2航天东方红卫星有限公司，北京 100094）

为了避免多路径噪声对低低星间跟踪（SST－LL）重力测量卫星K频段测距（KBR）系统测距精度的影响，基于SST－LL重力测量卫星的超静卫星平台，提出了一种磁控制与喷气控制相结合的KBR系统星间高精度指向控制算法。首先，利用喷气执行机构使卫星快速机动到目标姿态角；然后，利用磁力矩器和喷气执行机构对卫星进行联合稳定控制，在满足省电和节省喷气量的条件下，实现长周期、高精度的天线相对指向控制。利用“重力场反演与天气试验”（GRACE）卫星参数进行仿真验证，结果表明：在正常轨道运行模式下，该算法能实现俯仰和偏航方向优于1mrad的控制精度，可为KBR系统在轨高精度测距提供保证。

低低星间跟踪重力测量卫星；超静卫星平台；K频段测距系统；星间指向控制

1 引言

K频段测距（KBR）系统是低低星间跟踪（Satellite to Satellite Tracking Low－Low，SST－LL）重力测量卫星的关键载荷，采用双频双向载波相位对比技术测量2颗低轨小卫星的距离变化及其变化率，测距精度达到10微米级［1］。由于KBR系统本身无机械可转动对准机构，同时也没有星间链路信标信号，因此在运行过程中极易产生多路径噪声，严重影响KBR系统的测距精度。为此，必须研究应用于KBR系统星间指向的重力测量卫星姿态控制算法，使KBR系统天线指向与2颗卫星质心连线方向的夹角始终保持在1mrad以内［2］，从而消除多路径噪声对KBR系统测距精度的影响。

目前，应用于低轨小卫星且具有较高控制精度的控制技术，主要包括动量轮控制技术、喷气控制技术及磁力矩器控制技术。由于动量轮在姿态控制过程中会给卫星本体带来较高的加速度和频率噪声［35］，严重影响重力测量卫星静电加速度计等有效载荷的测量精度，不利于卫星的长周期、稳定运行，因此重力测量卫星平台不能安装动量轮。随着推进技术的发展，小推力喷气系统在小微卫星上获得了较多的应用［6－8］，但是卫星长期单纯依靠喷气进行KBR系统相对指向控制会耗费大量燃料，严重影响卫星的使用寿命。文献［9］中采用二次线性高斯方法对磁力矩器控制进行研究，结果表明，磁力矩器可有效应用于小角度时的3轴稳定控制，但是不能提供任意的控制指令。例如，当需要的磁力矩与地磁场矢量平行时，磁力矩器就不能提供需要的力矩，这时要喷气提供力矩进行补充，否则无法保持卫星姿态控制效果。综上所述，重力测量卫星须要采用喷气和磁力矩器的联合控制方式，并且喷气参与控制的时间应尽可能少，即“超静卫星平台控制技术”［10］。此控制技术已经在美国“重力场反演与天气试验”（GRACE）卫星上应用，控制精度在1mrad以内，但是其实现途径并未被公布。

本文从国内工程实际出发，提出了一种磁控制与喷气控制相结合的KBR系统星间高精度指向控制算法，其核心原理是根据SST－LL重力测量卫星中2颗卫星的相对位置，实时计算2颗卫星的俯仰偏置指令角，然后利用高精度控制算法使卫星的俯仰指向能够跟踪该动态变化的指令角数值，从而实现KBR系统的指向控制。控制算法分为姿态机动控制与姿态稳定控制2个阶段。在机动控制阶段，卫星经过速率阻尼后，相对惯性空间静止，由星敏感器测量确定出卫星的姿态四元数，用喷气执行机构快速机动到目标姿态位置。进入稳定控制阶段，为了减少喷气量，延长卫星寿命，利用磁力矩器和喷气执行机构联合控制，在满足省电和节省喷气量的条件下，实现KBR系统指向的长期、高精度控制，以保证KBR系统的测距精度。

2 KBR系统相对指向控制原理

KBR系统天线沿卫星本体坐标系X轴方向安装，因此卫星绕X轴的滚动对相对指向没有任何影响，为了实现KBR系统相互对准，仅须要针对卫星进行一定的俯仰和偏航通道偏置，就能实现星间高精度指向控制。图1示出了KBR系统星间指向原理，其中θ＊为卫星俯仰偏置指令角，XA和XB为卫星A和卫星B本体坐标系的X轴正方向，OA和OB为2颗卫星的质心，rA和rB为2颗卫星到地心的距离，Δu为纬度幅角。

当2颗卫星运行在同一近圆轨道上，姿态在偏航和滚动方向没有偏差时，俯仰偏置指令角近似为

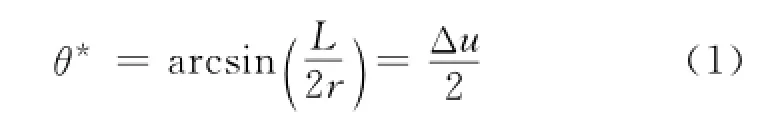
式中：L为双星距离；r为卫星到地心的距离，即rA或rB。

根据KBR系统指向与2颗卫星质心连线方向的夹角始终保持在1mrad以内的要求，主要有2种方法可实现KBR系统的高精度指向控制。①基于单颗卫星独自实施姿态控制，将姿态控制到目标姿态，以实现开环控制模式；②以一颗卫星的姿态为基准，将相对姿态测量信息作为另一颗卫星的控制输入，实现闭环控制模式。

开环控制模式需要的控制设备简单，基于单颗卫星的控制系统即可实现；而闭环控制模式要增加卫星相对姿态测量设备，闭环控制算法也相对复杂。因此，开环控制模式更有利于卫星的系统设计和设备研制，本文选择卫星A和卫星B独自进行姿态偏置，以达到KBR系统指向控制精度。

3 KBR系统相对指向控制算法

3．1 姿态机动控制阶段

控制之前的卫星飞行姿态为3轴稳定对地定向模式，在姿态机动阶段，为了使卫星迅速达到指定的姿态位置，采用喷气时间最优控制理论，控制期间磁控制停止。

卫星的实际姿态与目标姿态之间的夹角定义为拟欧拉角σ，其表达式为

式中：卫星的实际姿态q＝［q0q1q2q3］；目标姿态qf＝［q0fq1fq2fq3f］；G（qf）见式（3）。

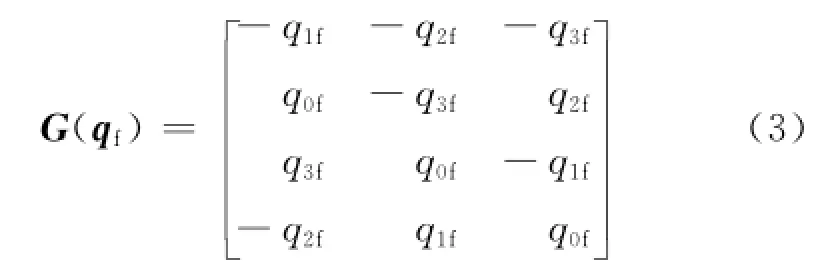
拟欧拉角速度σ·可表示为

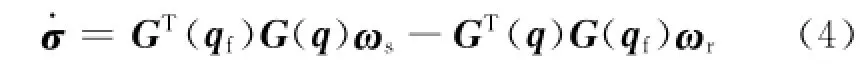
式中：ωs为轨道坐标系的绝对角速度；轨道坐标系的相对角速度ωr≈0。

当σ＝0，σ·＝0时，卫星姿态不但与目标姿态重合，而且相对参考坐标系静止，从而达到了高稳定度的控制目的。因此，本文控制算法的核心物理意义就是控制拟欧拉角和拟欧拉角速度到达原点，如图2所示。

图2中，OX1Y1Z1为卫星实际姿态坐标系；OX2Y2Z2为目标姿态坐标系；σx，σy，σz为目标姿态与实际姿态在3个轴的夹角。

当卫星实际姿态与目标姿态重合时，q≈qf或q≈－qf，则

式中：I为单位矩阵。

因此，式（4）可简化为

根据姿态动力学方程（忽略其他力矩的作用）可得

式中：Jp为卫星转动惯量；Tth为喷气力矩，见式（8）。

式中：Mth为3轴喷气力；滚动、俯仰和偏航通道开关指令δT＝［δxδyδz］。

将式（6）代入式（7），可得

由式（9）～（11），得到标称化拟欧拉角加速度方程为

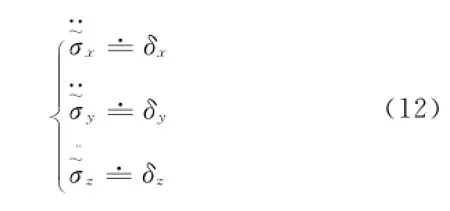
式（12）是3个结构相同的摄动双积分系统，根据双积分系统时间最优控制理论，得到时间最优控制律如下。

式中：下标a代表x，y，z，下同；滚动、俯仰、偏航通道的开关函数sa见式（14）。

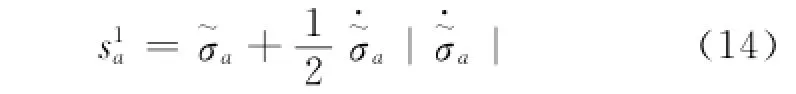
相位轨迹示意如图3所示。

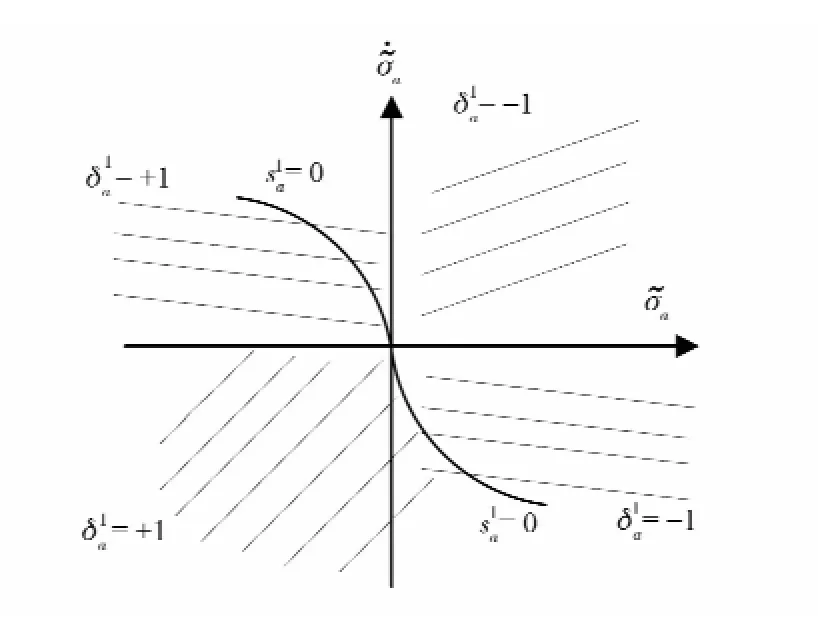
图3 最短时间喷气控制相位轨迹示意Fig．3 Phase track of the least time thruster control

3．2 姿态稳定控制阶段

利用姿态机动控制阶段使卫星迅速跟踪到目标姿态后，采用磁力矩器与喷气执行机构联合对卫星进行稳定控制，实现KBR系统长期、高精度的指向控制。

3．2．1 姿态稳定磁控制

根据3轴姿态确定的结果，用磁力矩器实现稳定控制，各种干扰力矩引起的姿态偏差则用3个正交的磁力矩器来修正，主动磁控制稳定回路采用比例差分（PD）控制算法，控制律的形式如下。

式中：Mc为磁控制力矩；Kd和Kp分别为阻尼系数和比例系数。

姿态稳定控制使σ＝0时，卫星实际姿态与目标姿态重合，达到了控制目的。

一般情况下，Mc不能由磁力矩器完全提供。在3维空间中，将其分解为两部分，一部分与地磁场矢量平行，一部分与地磁场矢量垂直，即

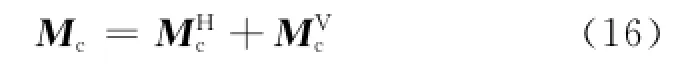
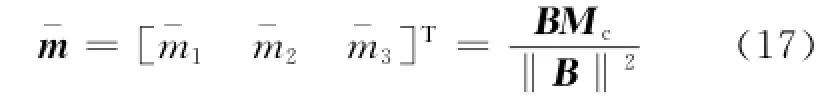
3．2．2 姿态稳定喷气控制

磁力矩器不能提供任意的控制指令，例如，当需要的力矩指令与地磁场矢量平行时，磁力矩器就不能提供需要的力矩，这时要由喷气执行机构提供力矩进行补充。为了节省气源，采用最省燃料控制模式（见图4），其极限环设置为1mard，即卫星实际姿态与目标姿态之间的夹角如果超过了1mard就进行姿态控制，否则不控制。

仍然采用拟欧拉角加速度方程，见式（12）。根据双积分系统燃料最优控制理论，得到燃料最优控制律如下。

式中：xmin，ymin，zmin分别为死区、干扰力矩和喷气时滞的控制补偿值，设置为［144 13 15］。

图4 最省燃料喷气控制相位轨迹示意Fig．4 Phase track of the least fuel thruster control

4 数学仿真

结合GRACE卫星的参数，对本文的控制算法进行仿真验证。卫星初始时刻为2015年1月1日12：00（UTC），飞行姿态为3轴对地定向模式，双星初始间隔220km，在地球惯性坐标系下的初始参数如表1所示。

卫星摄动力与环境力矩参数［11］：地球引力模型为10阶EMG96模型；大气阻力模型为DTM模型，大气阻力系数为2．2；太阳光压摄动模型中，太阳光压反照系数为0．5；地球磁场模型为13阶IGRF2005模型，卫星剩磁力矩为0．2A·m2。

执行机构参数［12］：滚动、俯仰和偏航的喷气力矩分别为0．006 9N·m，0．03N·m，0．03N·m。磁力矩器最大磁矩为30A·m2。

表1 卫星A和卫星B的初始参数Table 1 Initialization parameters of satellite A and B

根据式（1），随着卫星在轨运行，卫星摄动力不断改变，导致纬度幅角发生变化，因此俯仰偏置指令角也不断变化。图5为卫星A的俯仰偏置指令角曲线，要求超静卫星平台的俯仰指向能够跟踪该动态变化的指令角数值。从控制的角度看，俯仰偏置指令角很小，仅约为0．928°。卫星A和卫星B的结构完全相同，因此仿真结果中只给出了卫星A的控制结果，卫星B具有相同的结论。

图6为卫星A俯仰机动控制阶段的姿态控制精度，喷气执行机构时间延迟为0．2s。在机动过程中，磁控制不启动。可以看出：俯仰轴进入稳定状态的时间需要85s，而卫星初始实际姿态与目标姿态存在较大的滚动偏置角，导致滚动轴机动幅度比较大，进入稳定状态的时间需要220s。经计算，俯仰轴和偏航轴的控制精度均优于1mrad（3σ），滚动轴的控制精度优于10mrad（3σ）。因此，姿态机动控制算法可以满足高精度机动的需求。

进入稳定控制阶段后，姿态稳定控制算法的仿真结果如图7～10所示，仿真时间为11 000s。图7为稳定控制阶段的姿态控制精度，其中，俯仰轴、偏航轴姿态控制精度优于1mrad（3σ），滚动轴姿态控制精度优于10mrad（3σ）。图8为稳定控制阶段的卫星角速度，3轴角速度均优于0．001rad/s，稳定度优于0．000 1rad/s。可以看到，磁力矩器与喷气执行机构的联合控制可以达到稳定控制目的。图9为稳定控制阶段磁力矩的控制过程，可见，3轴磁力矩器很少超限幅工作。图10为喷气时间与飞行时间的关系，喷气时间总和少，喷气占时比为1∶385，即飞行385天需要单个推力器工作1天。如果换算成燃料消耗，就是平均每圈消耗燃料0．85g。按照这种使用频次，重力测量卫星在5年寿命期内姿态控制消耗燃料为23．27kg，可为整星质量预算、姿态控制分系统余量设计提供参考。

图7 稳定控制阶段的姿态控制精度Fig．7 Attitude control precision during stable control stage

图8 稳定控制阶段的卫星角速度Fig．8 Satellite angular rate during stable control stage

图9 稳定控制阶段磁力矩的控制过程Fig．9 Control process of magnetic torque during stable control stage

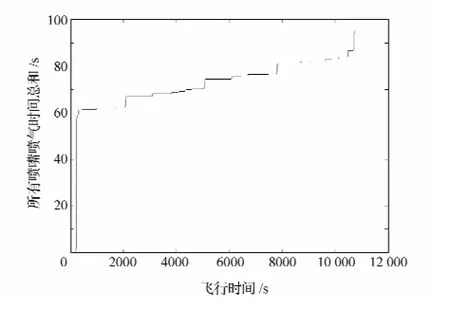
图10 喷气时间与飞行时间的关系Fig．10 Relationship between thruster time and flight time

5 结束语

KBR系统在轨应用的一个关键问题是如何设计高精度的卫星姿态控制算法，以保证其星间指向精度。针对这一问题，本文提出了一种磁控制与喷气控制相结合的KBR系统星间高精度指向控制算法。仿真结果表明：本文的控制算法具有较高的控制精度，控制律设计简便，可为超静卫星平台的控制方案设计提供参考。在后续的工作中，还要进一步结合喷气执行机构的具体工作特性进行深入研究，以更好地为重力测量卫星的工程化设计服务。

（

）

［1］刘晓刚，吴晓平，江东．低低卫－卫跟踪模式中星载KBR系统和GPS接收机指标设计论证［J］．武汉大学学报（信息科学版），2012，37（5）：35－40 Liu Xiaogang，Wu Xiaoping，Jiang Dong．Demonstration on the indexes design of space－borne KBR and GPS receiver in the low－low satellite－to－satellite tracking mode［J］．Geomatics and Information Science of Wuhan University，2012，37（5）：35－40（in Chinese）

［2］康开轩，李辉，吴云龙，等．重力卫星精密星间测距系统滤波器技术指标论证［J］．地球物理学报，2012，55（10）：3240－3247 Kang Kaixuan，Li Hui，Wu Yunlong，et al．Demonstration on the design of filter indexes of inter－satellite high accuracy ranging system for gravity satellite［J］．Chinese Journal of Geophysics，2012，55（10）：3240－3247（in Chinese）

［3］Chang Y K，Lee B H，Kim S J，et al．AUSAT－2nanosatellite ADCS performance analysis and commissioning［C］//Proceedings of the IEEE 2nd International Conference on Recent Advances in Space Technologies．New York：IEEE，2005：180－184

［4］李东．皮卫星姿态确定与控制技术研究［D］．上海：中国科学院上海微系统与信息技术研究所，2005 Li Dong．Study on attitude determination and control technology for pico satellite［D］．Shanghai：Shanghai Institute of Microsystem and Information Technology，Chinese Academy of Sciences，2005（in Chinese）

［5］Bang H，Young H L．Sliding mode control for spacecraft containing rotating wheels［C］//Proceedings of AIAA Guidance，Navigation，and Control Conference and Exhibit．Washington D．C．：AIAA，2001：1－8

［6］Hall C D，Tsiotras P，Shen H．Tracking rigid body motion using thrusters and momentum wheels［J］．The Journal of the Astronautical Sciences，2002，50（3）：311－323

［7］Bang H，Choi H D．Attitude control of a bias momentum satellite using momentum of inertia［J］．IEEE Transactions on Aerospace and Electronic System，2002，38（1）：243－250

［8］Antropov N N，Diakonov G A，Kazeev M N，et al．Pulsed plasma thrusters for spacecraft attitude and orbit control system［C］//Proceedings of the 26th International Propulsion Conference．Washington D．C．：PEPL，1999： 1129－1135

［9］马星宇．基于反作用飞轮和磁力矩器的卫星姿态控制系统研究［D］．哈尔滨：哈尔滨工业大学，2013 Ma Xingyu．Study on the attitude control system of satellite with reaction wheels and magnetors［D］．Harbin：Harbin Institute of Technology，2013（in Chinese）

［10］张沛，王永富．超静平台在卫星高精度高稳定度指向控制中的应用研究［J］．航天器环境工程，2007，24（3）：174－177 Zhang Pei，Wang Yongfu．The use of ultra quiet platform to achieve high pointing accuracy and high stability control of satellite［J］．Spacecraft Environment Engineering，2007，24（3）：174－177（in Chinese）

［11］Kim J R．Simulation study of a low－low satellite－tosatellite tracking mission［D］．Austin，Texas：University of Texas at Austin，2000

［12］Furun Wang．Study on center of mass calibration and K－band ranging system calibration of the GRACE mission［D］．Austin，Texas：University of Texas at Austin，2003

（编辑：夏光）

Algorithm of High Precision Inter－satellite Pointing Control for KBR System

XIN Ning1QIU Lede1ZHOU Na1ZHANG Lihua2
（1Institute of Telecommunication Satellite，China Academy of Space Technology，Beijing 100094，China）
（2DFH Satellite Co．，Ltd．，Beijing 100094，China）

In order to avoid the effect of multipath noise on ranging accuracy of SST－LL（satellite to satellite tracing low－low）gravity measurement satellite KBR（K band ranging）system，a high precision KBR system inter－satellite pointing control algorithm fusing magnetic control and thruster control is proposed based on ultra quiet satellite platform of SST－LL gravity measurement satellite．Firstly the thruster is applied to maneuver the satellite into the target angle attitude as fast as possible．Then the combination of magnetic torque and thruster torque is applied to realize the long－term and high precision pointing control under the circumstances of saving the finite electricity and fuel reserves．The simulation results by using GRACE satellite show that the attitude control precision of pitch and yaw angles can be better than 1mrad under the normal orbit moving mode，which can provide a guarantee for high accuracy ranging of KBR system．

SST－LL gravity measurement satellite；ultra quiet satellite platform；K band ranging system；inter－satellite pointingcontrol

V448．2

A

10．3969/j．issn．1673－8748．2016．02．006

2015－09－02；

2015－11－10

国家高技术研究发展计划（863计划）（2012AA01A504），国家自然科学基金（91438205）

辛宁，男，博士，研究方向为卫星系统总体设计。Email：xinning7@sina．com。