离心压气机气动噪声数值预测

覃玄，姚胜华

（湖北汽车工业学院汽车工程学院，湖北十堰442002）



离心压气机气动噪声数值预测

覃玄，姚胜华

（湖北汽车工业学院汽车工程学院，湖北十堰442002）

摘要：以CFD软件为平台，计算得到不同工况下离心压气机定常流动特性曲线，验证模型正确性。将定常计算结果作为初场，对不同工况下压气机非定常流场进行数值模拟，获取流场内部声源强度信息。基于间接边界元法，将离心叶轮简化为旋转偶极子，计算离心叶轮辐射声场。结果表明：离心叶轮为压气机主要噪声源，由动静子相互干涉作用产生的离散噪声为主要噪声类型。

关键词：离心叶轮；非定常流动；离散噪声；间接边界元

涡轮增压器作为增压装置被广泛应用于各种船用柴油机。为了最大限度提高柴油机的动力性能，满足现代船舶大型化、高速化发展趋势，涡轮增压器正向高增压、高转速、高效率以及更宽广的运行范围方向发展。随着船舶噪声控制标准的提高，涡轮增压器气动噪声问题逐渐成为研究重点。离心压气机作为涡轮增压器的重要组成部分，引发的气动噪声也是涡轮增压器的主要噪声源之一，因此压气机气动噪声研究对于增压器降噪具有十分重要的意义。

离心压气机是由相互接触的转子和静子组成的叶轮机械。随着计算机硬件技术的发展，越来越多国内外学者开始采用计算流体力学（CFD）结合声学理论研究叶轮机械气动噪声［1］。Hyosung Sun和Soogab Lee采用Euler方程求解流场，结合声学边界元（BEM）方法求解声场，成功预测了离心式压气机内外声场分布［2］。毛义军、刘秋洪等人基于非定常流场，结合声类比、大涡模拟、涡声理论等声学计算方法，对离心风机内部气动声源特性进行分析研究［3-5］。Yutaka Ohta和Nobumichi Fujisawa采用分离涡模拟法（DES）成功预测了锥形扩压器叶片对于压气机气动性能的影响［6］。本文中对某型船用离心压气机采用CFD软件进行定常流动数值求解，得到工作特性曲线，以定常流动结果为初场，进行三维非定常流动数值模拟，获取声源信息，基于声学计算软件Virtual.Lab Acoustics结合间接声学边界元法预测离心叶轮离散噪声辐射声场。1.1研究对象

以某型船用涡轮增压器离心压气机（图1）为研究对象，该离心压气机由进气道、离心叶轮、有叶扩压器以及蜗壳组成。表1给出了叶轮及扩压器基本参数。

图1　压气机几何模型

1　研究对象及数值模拟方法

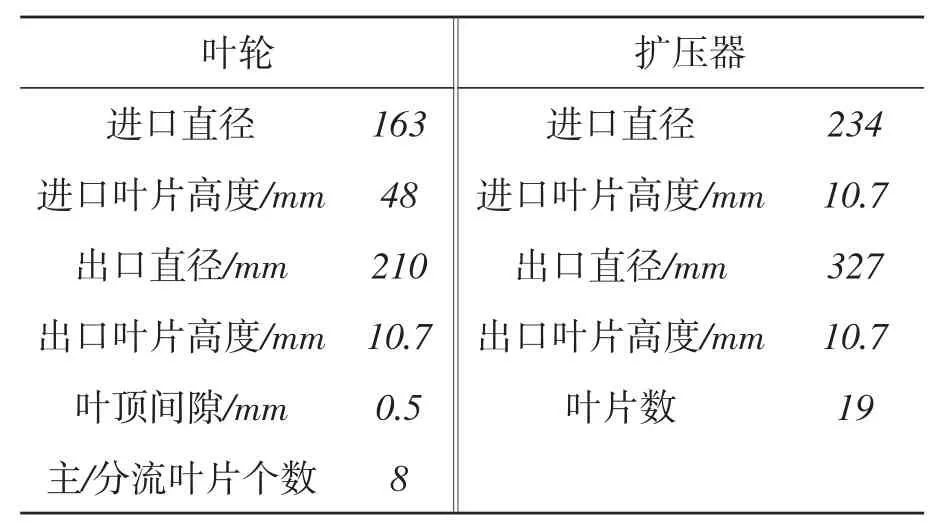
表1　压气机基本参数

1.2流场数值模拟方法

使用常用CFD软件CFX进行压气机全周流场数值模拟，通过求解N-S方程，计算额定转速下压气机特性曲线。定常计算时，选择理想气体作为场内流体，参考压力设为0 Pa，标准k-ε湍流模型。叶轮与扩压器交界面设为冻结转子（FROZEN RO⁃TOR）交界面。边界条件根据实验已知特性曲线给定进口总压、进口总温以及出口静压。计算结果以残差达到10-5为收敛标准，此标准满足工程应用的要求。非定常流场计算以定常计算结果为初场，计算总时间为压气机转5圈的时间0.006 58 s，压气机旋转1°时长为时间步长，经计算为3.66×10-7s，内部迭代步数为20。在计算过程中将动静交界面设为TRANSIENT ROTOR-STATOR。

压气机计算网格如图2所示，叶轮及扩压器网格采用分块技术自动划分，并对其加密，网格总数为4 322 304，蜗壳采用非结构网格，对固壁面进行加密，网格总数为540 315。

非定常计算时，在流场内设置静压监测点。监测点位置如图3所示。P1～P5位于叶轮前缘附近，P6～P10位于叶轮尾缘附近，P11～P13分别位于扩压器流道的前缘、尾缘以及出口。

图2　离心压气机网格

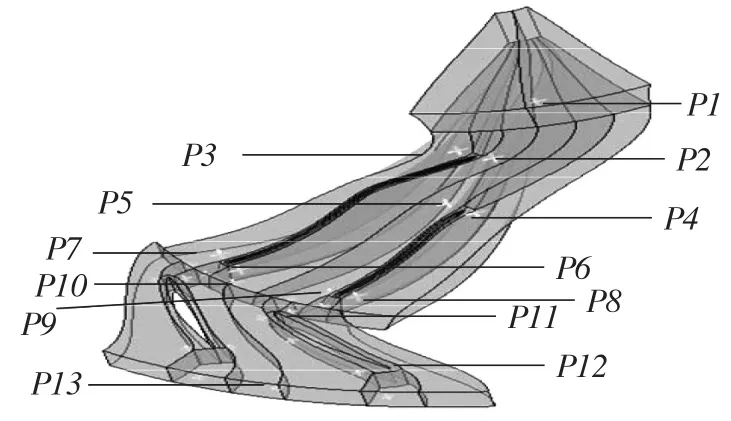
图3　监测点示意图

1.3声场数值模拟方法

选择LMS Virtual.Lab Acoustics软件声学边界元模块计算压气机旋转叶轮的辐射声场。

边界元法是根据积分定理，把区域内的微分方程转换成边界上的积分方程，然后分割边界成有限大小的边界元素，最后把边界积分方程离散成代数方程。边界元法包括直接边界元法和间接边界元法。声学边界元可以有效计算辐射声场。其中，采用直接边界元法进行数值模拟时，要求面网格必须是封闭的，可以分别计算模型的内声场以及外声场，但不能同时得到内外声场。采用间接边界元法进行声学计算时，面网格可封闭可不封闭。

采用ICEM划分包围着叶轮和扩压器的不封闭边界模型面网格，计算过程中网格类型设置为Acoustical，流体材料为air，空气属性为默认设置。将扩压器出口面定义为无反射边界条件，此处声波不发生反射，作为透设处理。罩壳壁面定义为绝对硬壁面，将壁面对声场的影响考虑进去。辐射场位于叶轮出口垂直于出口平面，是边长为1 000 mm的正方形平面场。

2　流场计算结果分析

2.1计算结果验证

图4给出了定常计算得到不同转速下的压气机工作特性曲线并与已知的实验数据进行对比。由图可知，计算结果与实验数据匹配良好，误差保持在8%范围内。产生误差的主要原因为在建模过程中对压气机进行了合理的简化，忽略了进口扰动对于流场的影响，忽略了叶顶间隙的变化以及没有考虑压气机与外界环境的换热作用［6］。

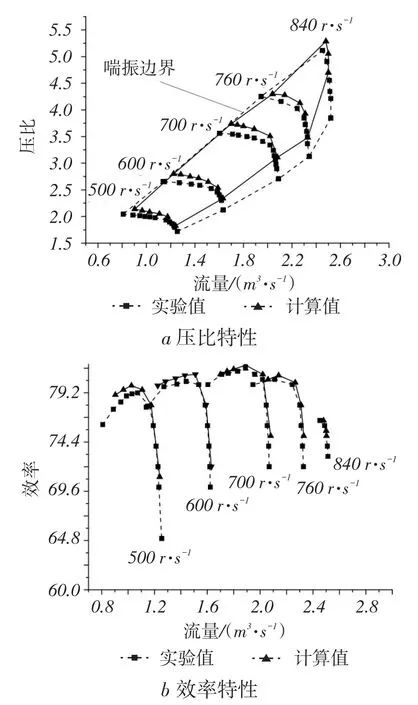
图4　特性曲线对比图

2.2流场分析

当压气机达到稳定运行状态时，提取一个周期内某一时刻的静压云图进行分析，如图5所示。经过叶轮、扩压器、蜗壳气体压力逐渐升高，在蜗壳出口压力达到最大。

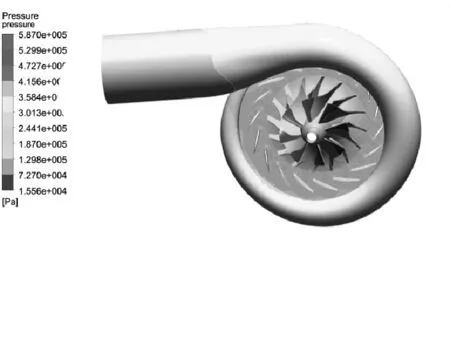
图5　整机静压分布云图

观察发现在叶片前缘吸力面一侧、叶轮尾缘以及扩压器前缘压力温度变化剧烈，涡流明显，蜗壳流道内压力分布均匀。图6所示为压力、温度分布局部放大图。叶片前缘涡流主要受到叶顶间隙影响，叶顶间隙的存在使动叶压力面和吸里面之间发生压差流动，气体在叶尖和罩壳环壁之间相对运动，最终形成二次流、间隙流等不规则涡流。叶轮尾部以及扩压器前缘压力、温度分布不均匀，叶轮尾缘分流叶片与主叶片之间存在由尾迹涡流和尾部旋涡引起的局部高温高压区，高速气体经叶轮出口流入扩压器，猛烈撞击扩压器叶片前缘，形成小范围的湍流脉动。根据气动噪声产生机理，初步分析，湍流脉动强烈的叶轮前缘、尾缘以及扩压器流道为主要噪声源。

图6　压力及温度分布局部放大图

3　声场计算结果

声强用于评价垂直于传播方向单位面积上通过的平均声能量大小，声强计算公式为

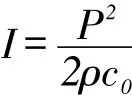
式中：P为频域特性下的压力脉动；ρ为空气密度，计算中假设空气密度保持不变，取1.29 kg·m-3；c为声速，取340m·s-1；基准声强I0为人耳可听最小声强，取10-12。通过傅里叶变换得到的声强频谱图如图7所示。该转速下基频为760 Hz，主叶片和分流叶片个数均为8。

由图7a可知，在叶轮前缘附近产生与基频相关的离散噪声，声强级在基频760 Hz和二次谐波处出现峰值，最大峰值为基频处，此时声强级为142dB，该处离散噪声主要是由于叶尖不规则运动与静叶相互干涉引起。

由图7b知，叶轮流道尾缘主要噪声源即与叶片通过频率相关的离散噪声，6080 Hz、12160 Hz、18240 Hz处均出现声强级峰值，其中在12160 Hz处各监测点声强级都出现最大峰值，P9点声强级最大为170dB。这说明叶轮尾缘离散噪声主要由主叶片和分流叶片共同扰动引起的湍流脉动与静叶相互干涉形成。

分析扩压器流道声强级频谱图（图7c）可知，流道内噪声表现出明显的离散性，在6080 Hz、12160 Hz、18240 Hz处均出现声强级峰值，其中在6080Hz处各监测点声强级都出现最大峰值，各监测点最大峰值基本一致为165dB，随着谐次的增加，离散噪声逐渐减弱。扩压器流道内的离散噪声主要受到主叶片扰动作用影响。

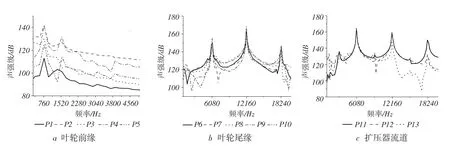
图7　叶轮及扩压器流通声强级频谱图

从上述分析可得，由动静子相互干涉引起的离散噪声在压气机气动噪声中占据主导地位，其中旋转叶轮为主要噪声源。将叶轮简化为旋转偶极子声源，基于声学计算软件Virtual.Lab结合间接声学边界元法预测离心叶轮离散噪声辐射声场。

计算得到主叶片通过频率和整周叶轮叶片通过处的辐射场点声压级云图（图8）。不同频率处，声压分布发生变化，整周叶片通过频率处，管口附近辐射声压较高，最大为137 dB。叶片通过频率属于高频，此时声波波长小于管口直径（163 mm），在管口出发生了反射现象。

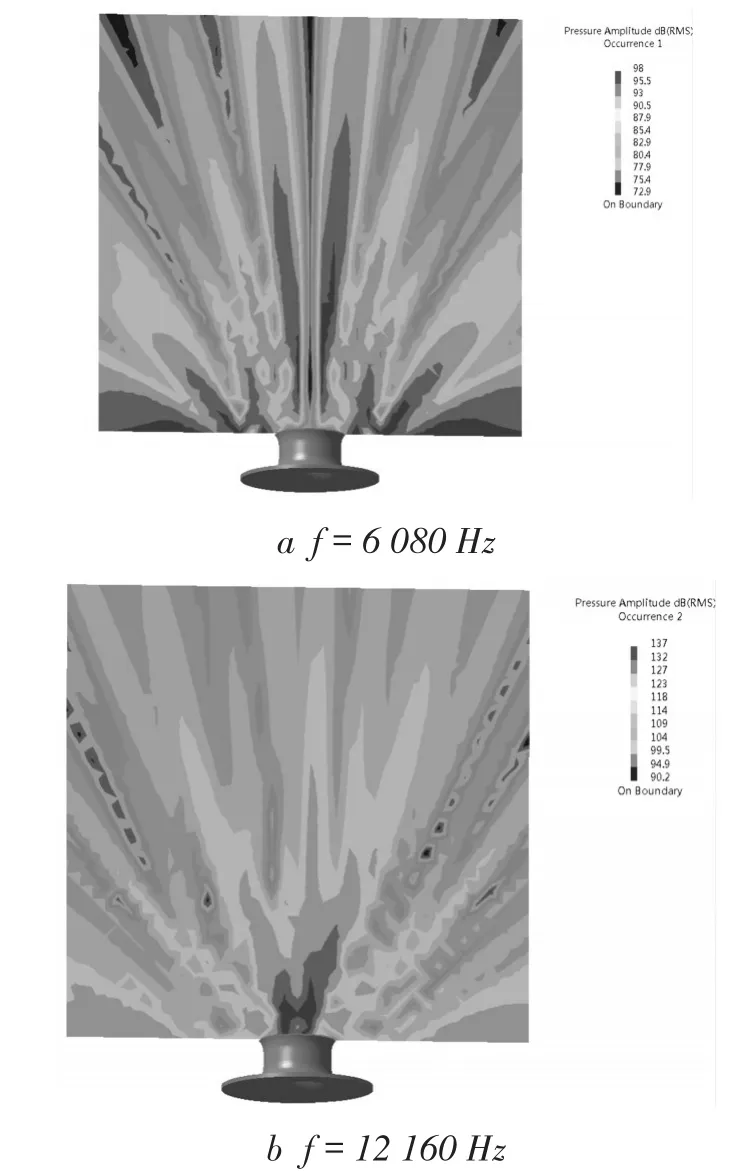
图8　辐射场点声压级云图

4　结论

压气机内部叶轮前缘、尾缘以及扩压器流道内，湍流脉动强烈，为主要噪声源。

对于本文中所研究的高速离心压气机离散噪声为主要噪声源。叶轮前缘噪声源主要为由叶尖不规则运动与静叶相互干涉引起的离散噪声，强度较弱；叶轮尾缘以及扩压器流道内噪声源主要为叶轮尾迹涡流与静叶相互干涉引起的离散噪声，强度较大，决定了整台压气机的噪声级。

将叶轮简化为旋转偶极子声源，结合间接声学边界元法预测离心叶轮离散噪声辐射声场。不同频率处，场点声压分布发生变化，整周叶片通过频率处，管口附近辐射声压较高。

参考文献：

［1］毛义军，祁大同.叶轮机械气动噪声的研究进展［J］.力学进展，2009，39（2）：189-200.

［2］Sun H，Lee S. Numerical Prediction of Centrifugal Com⁃pressor Noise［J］. Journal of Sound and Vibration，2004，269（1）：421-430.

［3］毛义军，祁大同，刘秋洪.基于非定常流场的离心风机气动噪声分析［J］.西安交通大学学报，2005，39（9）：989-993.

［4］Q Liu，D Qi，Y Mao. Numerical Calculation of Centrifu⁃gal Fan Noise［J］. Mechanical Engineering Science，2006，220（8）：1167-1178.

［5］Y Mao，D Qi. Computation of Rotating Blade Noise Scat⁃tered by a Centrifugal Volute［J］. Power and Energy，2009，233（8）：965-972.

［6］Yutaka Ohta，Nobumichi Fujisawa. Unsteady Behavior and Control of Vortices in Centrifugal Compressor［J］. Journal of Thermal Science，2014，23（5）：401-411.

［7］祁明旭，原野，马朝臣.离心压气机非定常流动频域特性［J］.工程热物理学报，2009，30（9）：1475-1478.

Numerical Prediction of Aerodynamic Noise for Centrifugal Compressor

Qin Xuan, Yao Shenghua
（School of Automotive Engineering, Hubei University of Automotive Technology, Shiyan 442002, China）

Abstract:Based on CFD software, the performance curves of the steady flow were obtained on a centrif⁃ugal compressor under different conditions, and the validation was confirmed. The steady numerical re⁃sults were served as initial condition, the unsteady numerical simulation under different conditions was carried out and the sound source information was then obtained. Based on the indirect boundary ele⁃ment method, the centrifugal impeller was simplified as the spinning dipole to calculate the radiated sound field. The results show the centrifugal impeller is the main noise source, the discrete noise caused by the interference effect between the stator and rotor is the main noise type.

Key words:centrifugal impeller；unsteady flow；discrete noise；indirect boundary element method

作者简介：覃玄（1990-），女，湖北荆门人，硕士，从事内燃机性能研究。E-mail：qinxuan66@163.com

收稿日期：2015-11-10

doi：10.3969/j.issn.1008-5483.2016.01.008

中图分类号：TB533+.1

文献标识码：A

文章编号：1008-5483（2016）01-0030-04