寓数于形，以形解数

蔡少林

摘 要：“数形结合”是数学学习中的重要思想。对于高中数学的学习，教师应该在日常教学当中培养学生的“数形结合”思维模式，这样可以降低学生理解知识的难度。通过对图形的講解，真正达到化难为易的目的，促进学生对知识的掌握。

关键词：高中数学；“数形结合”；思维能力

从数学的整体构成来说，“数”与“形”两者之间是相辅相成的，只有做到两者的有机融合，才能够真正锻炼学生的数学思维，提高其数学应用能力。高中数学知识较为复杂，而且题目的综合性较强。所以，如果能将“数形结合”的思想运用到教学过程中，将极大地促进学生的数学学习。

一、高中数学应用“数形結合”思想的意义

人脑对图形的感知要远远强于对抽象数字的认识。所以，在日常教学中，教师应该有意识地运用图形展示数学内容。在高中数学中，从集合、函数到不等式，再到之后的证明与概率，这些知识点具有较强的逻辑性。高中数学知识点的难度逐渐增加，而且考查的内容也比较全面，如果教师能够用“数形结合”的思想帮助学生梳理知识，那么学生就会对高中数学知识形成体系化的理解。在“数形结合”思想的引导下，学生在解题时能够找准题目的关键，节省思考的时间。另外，运用“数形结合”的方法也能够更好地培养学生的逻辑思维能力，从而在根本上提升其解题能力。

二、高中数学应用“数形结合”思想的具体策略

1.深入挖掘课本知识

教师要深入挖掘课本知识，确定哪些知识可以运用“数形结合”的思维方式降低解题难度。教师在备课阶段要做好准备工作，从学生的学情出发，对教材内容进行分析。教师要构建有层次、有结构的数学课堂，要熟悉教材内容，真正用好教材。而学校也要为教师提供必要的交流平台，使教师不断提高自己的教学水平。

2.帮助学生真正理解“数形结合”的思想

数学学习更是一种能力的培养。尤其是高中数学，如果教师能够使学生灵活运用知识，那么其教学就是成功的。所以，教师需要引导学生从题目出发，运用“数形结合”思想学习理论知识。这一点看似简单，但其实需要学生积累一定的理论知识后不断练习才能有所收获。学好数学才是倡导“数形结合”思想的根本目的。

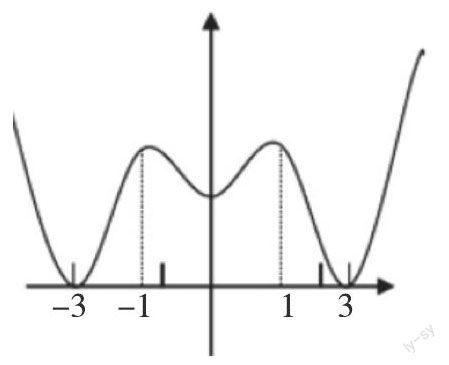
函数单调区间的问题通常可借助函数图像解答。学生可根据函数的定义域和图像，确定其单调区间。比如，求函数y=|x2-2|x|-3|的单调区间。此题若用分类讨论方法，不结合图像，情况会比较复杂，而且容易遗漏、出错。学生首先判断出该函数是偶函数，然后画出函数x≥0的图像，再画出关于y轴对称的图像，得到下图所示的图像。 从图中可得： 在[-3，-1]，[0，1]，[3，+∞）为函数y增区间；在（-∞，-3]，[-1，0]，[1，3]为函数y减区间。

3.有针对性地对学生进行指导

目前，教师还是依据分数来衡量一个学生的学习情况，这种衡量标准存在很大的片面性。从数学这门学科的特点来说，我们可以发现许多影响考试发挥的因素。所以，有必要从多方面对学生进行评价，改变以分数论成败的单一评价模式，这样对培养学生的“数形结合”思维也是有帮助的。而对于学生练习中的错题，教师也需要有针对性地进行指导。学生如果找准解题窍门，会发现高中数学题目其实并不难，而“数形结合”正是起到了启发学生思路的作用。这样，学生在解题过程中会少走很多弯路，从而真正做到“寓数于形，以形解数”。

三、总结

高中数学学习是有一定的方法和技巧的，看似复杂的知识背后其实是具有关联性的。数学学习提倡“数形结合”，这样才能真正使学生思维发散，实现以形解数。虽然目前很多教师已经意识到“数形结合”思想对高中数学教学的意义，但是其应用过程当中仍然存在许多问题，其中的一些细节还有待教师逐步完善。

参考文献：

[1]王丽娜.关于高中数学课堂教学有效性的研究[D].西安：陕西师范大学，2013.

[2]陈建敏.高中数学概念教学之翻转课堂理念下的教学模式探究[D].成都：四川师范大学，2015.