基于相异边际成本的多个厂商动态古诺模型分析

摘要：本文把两个厂商条件下的古诺模型拓广到更为一般情形，并进行动态分析，研究不同边际成本条件下多个寡头厂商的一般动态古诺模型。在给出一般动态古诺模型的数学表达式的基础上，列出各寡头厂商不同阶段的产量的表达公式，得出了各寡头厂商的均衡产量表达式，编程精确地实现了每一步动态博弈结果，并将不同条件下的动态博弈结果进行了比较，证明了成本对均衡产量的影响：边际成本对均衡产量有负的影响，边际成本小的厂商具有成本优势。

关键词：边际成本；寡头厂商；动态古诺模型

中图分类号：F224 文献标识码：A

收稿日期：2015-07-09

作者简介：高静（1984-），女，河北秦皇岛人，上海财经大学经济学院博士研究生，研究方向：空间计量经济学诊断、西方经济学理论及应用。

寡头垄断市场是指只有少数几个厂商竞争的一种普遍存在的市场结构，在该市场中，一定数量的生产同质商品的厂商必须在考虑其他厂商行为策略的基础上制定自己的产量决策。1838年，法国经济学家古诺（Cournot） 在《对财富理论的数学原理的研究》一文中，首次给出了寡头垄断市场中的两个厂商关于产量博弈均衡的古诺模型。最初的古诺模型仅涉及两个生产厂商，而且两个厂商的边际成本均为零，是一种比较特殊的情形。然而在现实的经济活动中，普遍存在的是多个生产厂商共同博弈的情形，各厂商生产商品时具有一定的边际成本，而且各寡头厂商因厂商规模、生产技术、管理等因素必定造成不完全相同的边际成本。该模型经过不断发展和改进，已经成为分析寡头垄断市场中各厂商生产行为的应用最广的模型之一，其中研究一定时期内寡头垄断者之间进行多次产量博弈的古诺模型称为动态古诺模型，而且参与古诺博弈的厂商也由原来的两个增加到了多个。Bresnahan和Reiss（1991）研究了厂商数量对市场价格的影响[1]，Terrance和Jason（1998）描述了双头垄断厂商在信息不对称情况下的竞争行为[2]，Dolores和Amparo（1999）研究了双头垄断在市场价格不明情况下的学习行为[3]，Bischi和Naimzada（1999）研究了一个具有线性成本的有限理性的双寡头博弈模型[4]，Agiza和HegaziA（2001）研究了具有非线性成本的有限理性多寡头博弈模型[5]，Harrison（2001）给出了一个在价格不确定的情况下的重复博弈的例子[6]。另外，张明善和唐小我（2002）探讨了多个厂商零成本条件下序贯动态博弈时最优产量的数学表达式，并从理论上证明了均衡解的存在性[7]；Normann（2002）、Bischi和Lamantia（2002）、Matsumura（1999）以及Agiza和Hegazi（2002）等人研究了不完全信息、有限理性、溢出效应等因素对厂商的影响，给出了对应情况下动态模型的最优产量解及其分析[8-11]；闫安和达庆利（2006）讨论了两厂商序贯博弈的动态古诺模型，在模型中引入成本因素，依据产品的市场容量随时间发生变化的特点，修正了两厂商序贯博弈的动态古诺模型[12]；陈署和姚洪兴（2006）证明了多组动态古诺模型是存在稳定性的，同组的厂商通过适当的调整利润分配，能够达到帕累托最优状态[13]；达庆利和闫安（2007）研究了相异成本情形下的耐用品动态古诺博弈情形，并建立了具有相异成本的两个厂商同时博弈时的动态古诺模型[14]。本文在上述文献研究的基础上，建立了不同边际成本下任意多个厂商条件的一般动态古诺模型， 把两个厂商条件下的古诺模型拓广到了更为一般情形， 并进行了动态分析，给出了一般动态古诺模型的数学表达式，得出各厂商的均衡产量的计算公式，并通过编程将问题加以程序化，与各种特殊动态博弈结果进行了比较。

一、相异成本条件下多个厂商的动态古诺模型

根据以上所述，给出不同边际成本下多个生产厂商一般动态古诺模型的假设条件，具体件如下：

（1）参与博弈的为生产同质产品的n家寡头厂商进行博弈，它们根据其余厂商的产量选择自己的产量以实现当前阶段厂商自身利润最大化。

二、模型结论分析

通过对参与博弈的厂商数目及其边际成本加以限制，可得出以下结论：

（1）参与博弈的厂商只有两个且其边际成本为零时，即n=2，且c1=c2=0，带入（11）式，可得到每个厂商的均衡产量为Q1=Q2=a3b。此时，符合经典双寡头模型博弈结论。

（2）参与博弈的寡头厂商有多个且其边际成本为零时，即c1=c2=…=cn=0，可得到每个厂商的均衡产量为Q1=Q2=…=Qn=ab（n+1）。此时，符合零成本条件下多厂商的动态古诺模型博弈结果，与张明善和唐小我（2002）所得到的结论相同。

（3）参与博弈的寡头厂商有多个且存在边际成本且均相同时，即c1=c2=…=cn=c，得到每个厂商的均衡产量为Q1=Q2=…=Qn=a-cb（n+1）。此时，符合考虑了等成本条件下多厂商的古诺模型博弈结果，与郑宏星（2008）[16]所得到的结论相同。

三、算例分析

为说明边际成本对动态博弈结果的影响，笔者针对（3）式中的函数形式写了一个C++计算程序以演算各阶段动态博弈结果（程序源代码见附录）。在程序中，需要输入的数据变量有：（1）博弈次数；（2）参与博弈的公司数目；（3）市场需求曲线的系数a，b；（4）参与博弈各厂商的标记生产成本。通过对各个输入数据的控制，程序能够很快的计算出不同情况下的动态博弈结果。为使程序结果更加接近真实情况，笔者将数据精度设置到小数点后十位。

下面，笔者将用该程序求解个寡头边际成本为零、边际成本都相同和边际成本不全相同情况下多厂商的动态博弈结果，并对结果加以比较，以说明成本对均衡产量的影响。考虑一个具有5个生产厂商的古诺模型. 设博弈前市场需求曲线为P=1-Q， 各厂商的产量记为Qi（m）。

（1）边际成本均为零时，即（c1=c2=…=c5=0），博弈结果如表1所示。

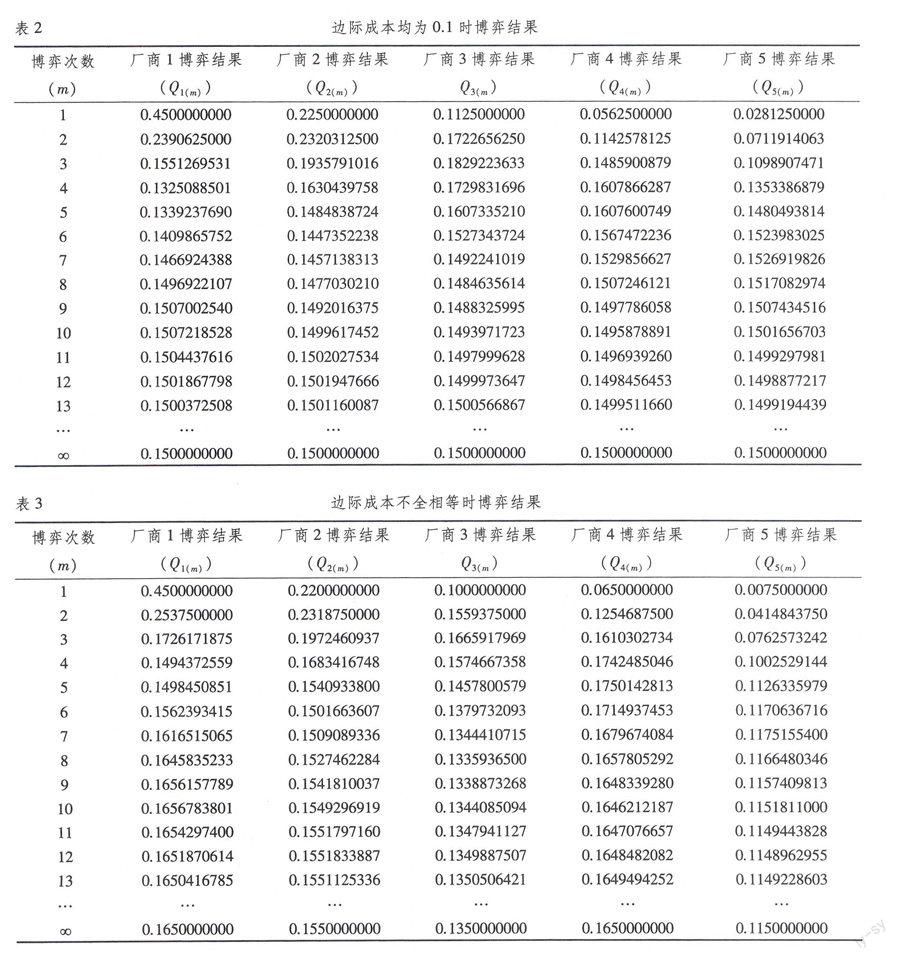
通过输入不同的动态博弈次数，笔者发现当进行第13次博弈以后，各厂商产量基本上达到了均衡。通过以上三个表格，可以得出以下结论：

（1）边际成本对均衡产量产生负的影响，由表1和表2可知，边际成本存在的情况下要比边际成本为零时的产量低。

（2）边际成本对各厂商均衡产量有很大影响，边际成本小的厂商可获得较大的均衡产量，而边际成本相对较大的厂商获得的均衡产量要相对少一些，即边际成本小的厂商具有成本优势。由表3可知，厂商1的边际成本c1=01，所得到的均衡产量为0165，而寡头厂商5的边际成本c5=015时，所得到的均衡产量只有0115，由此可见边际成本对均衡产量的影响是不容忽视的。

参考文献：

[1] Bresnahan T， Reiss P.Entry and competition in concentrated market[J].Journal of Political Economics， 1991，99：977-1009.

[2] Terrance M Hurley， Jason F Shogren.Effort levels in a Cournot Nash contest with asymmetric information[J].Journal of Public Economics，1998，69（2）：195-210.

[3] M Dolores A lepuz， Amparo Urbano.Dupoly experimentation： Cournot competition[J].Mathematical Social Sciences， 1999，37（2）：165-188.

[4] Bischi G I， Naimzada A.Global analysis of a dynamical duopoly game with bounded rationality[A].Advanced in Dynamical Games and App lication[D].Basel： Birkhanser，1999.

[5] Agiza H N， HegaziA S. The dynamics of bowleys model with bounded rationality[J].Chaos， Solitons and Fractals， 2001，12：1705-1717.

[6] Harrison Cheng. Cournot outcome and optimal collusion： an example[J].Economics Letters， 2001，74（1）：1-8.

[7] 张明善，唐小我.多个生产商下的动态古诺模型分析[J].管理科学学报，2002，5（5）：85-90.

[8] Normann H. Endogenous timing with incomplete information and with observable delay[J].Games and Economic Behavior，2002（39）：282-291.

[9] Bischi G I，Lamantia F. Nonlinear duopoly games with positive cost externalities due to spillover effects[J].Chaos， Solitons and Fractals， 2002，13（4）：701-721.

[10]Matsumura T.Cournot duopoly with multi-period competition： Inventory as a coordination device[J].Australian Economic Papers，1999（9）：189-202.

[11]Agiza N H， Hegazi S A， Elsadny A A. Complex dynamics and synchronization of duopoly game with bounded rationality[J].Math-ematics and Computers in Simulation，2002，58（2）：133-146.

[12]闫安，达庆利.两厂商序贯博弈的动态古诺模型[J].系统工程理论方法应用，2006，15（2）：103-106.

[13]陈曙， 姚洪兴.多组动态古诺模型的稳定性分析[J].复杂系统与复杂性科学，2006，3（3）：48-55.

[14]达庆利， 闫安.相异成本情形下的耐用品动态古诺模型研究[J].管理工程学报，2006，21（3）：56-59.

[15]翟运开， 李海婴，董芹芹.基于古诺模型的战略联盟合作效应研究[J].科技管理研究，2007（6）：268-270.

[16]郑宏星.产业集群演进的制度分析[M].北京：中国社会科学出版社，2008：88-91.

Abstract：This paper generalizes the Cournot model with two firms to general dynamic Cournot model and carries out dynamic analysis to study general dynamic Cournot model of multiple oligopoly firms under the condition of different marginal costs. Given the mathematical expression of the general dynamic Cournot model， the paper lists the optimum yield expression formula of each oligarchic firm， calculating the equilibrium output expression formula of each oligarchic firm， and then realizes the result of dynamic game step by step accurately by programming. Compared with the results of the dynamic game under different conditions， it is found that the cost can affect the equilibrium output： marginal cost has a negative effect on equilibrium output， and companies with small marginal cost have cost advantages.

Key words：marginal cost； oligopoly firms； dynamic Cournot model

（责任编辑：李江）