利用系统理论的观点学习高等数学

郑锐丽 吴泽宾

摘 要：本文主要应用系统理论的观点，结合部分高等数学教学经验，指出把“学习高等数学”看作一个系统，分析该系统的组分、结构、子系统。并试着利用系统的多样性、整体性、相关性理论理解各个系统，从而启示学者如何学好高等数学，为学习者学好高数提供思考，拓宽系统理论的实际应用。

关键词：系统；子系统；学习；高等数学

高等数学是大学学习的基本内容，更是理工科学生学好专业课的基础理论支撑。然而，大部分学生对高等数学的学习存在畏难心理，对某些知识点理解不够全面、深刻，更不能培养学生解决问题的数学思维能力。系统的相关性、整体性、多样性观点启示我们在学习高等数学时，要联系自身情况分析学习效果，思考各知识模块之间的联系和区别，并从整体的角度看待“学习高等数学”这个过程。避免“只见树木，不见森林”的局限思维，不再只是哪个知识点不会学哪个，而是要带着动态联系的思维方式来学习。

1 系统的阐述

系统是指由若干要素相互作用、并以一定的结构形式复合组成的、在特定的外部环境下具有某种特定功能的有机整体。[ 1 ]一切事物都不可能孤立于周围的环境，事物的内部必定存在相互关联的事物子群体，因而我们都可以利用系统的观点来描述和分析。组分是指事物中包含的各个部分，不可再细分的组分称为系统的要素或元素。系统的特性包括整体性、相关性、多样性等。

1.1 整体性

整体性指系统具有其整体的布局、整体的行为方式、整体的特性、整体的功能、整体的发展方向，与外部其他系统整体的联系等。[ 2 ]高等数学知识具有整体的解题思路、整体的知识结构、整体的数学思维方式、整体的逻辑结构、整体的对理工学科产生的整体辅助作用等。

1.2 相关性

相关性指系统内部不存在孤立的组分，任一组分或元素必定以系统或自身的发展为前提，与其他要素或组分相互关联、相互依存、相互牵制、相互促进等。学习者学习高等数学的过程中，学习者的学习方法与学习者的学习效率密切相关，两者间相互作用，相互促进或相互牵制。

1.3 多样性

多样性指系统内部组分或要素、关系等的多元化、差异性，系统是多样性的统一。学习者的学习动机、学习方法、学习工具、学习评价或效果、自身基础、高等数学知识是系统的组分，这些组分相互之间既有区别又有联系，体现了系统的多样性或差异性。

1.4 系统的结构和系统的可分性

系统的结构指各组分之间相互关联方式的总和。

系统的可分性或划分子系统是指当系统的组分或要素的数量较多，且彼此之间存在较大的差异，为了方便系统分析，可以将特点相同或相近的组分或要素合并起来，形成若干子系统。若利用集合的思想来描述，可设表示某个系统，表示其元素或组分集合，根据子系统与系统间的关系，有，称为系统的子系统，且具有系统的特性。[ 6 ]

2 如何利用系统理论学习高等数学

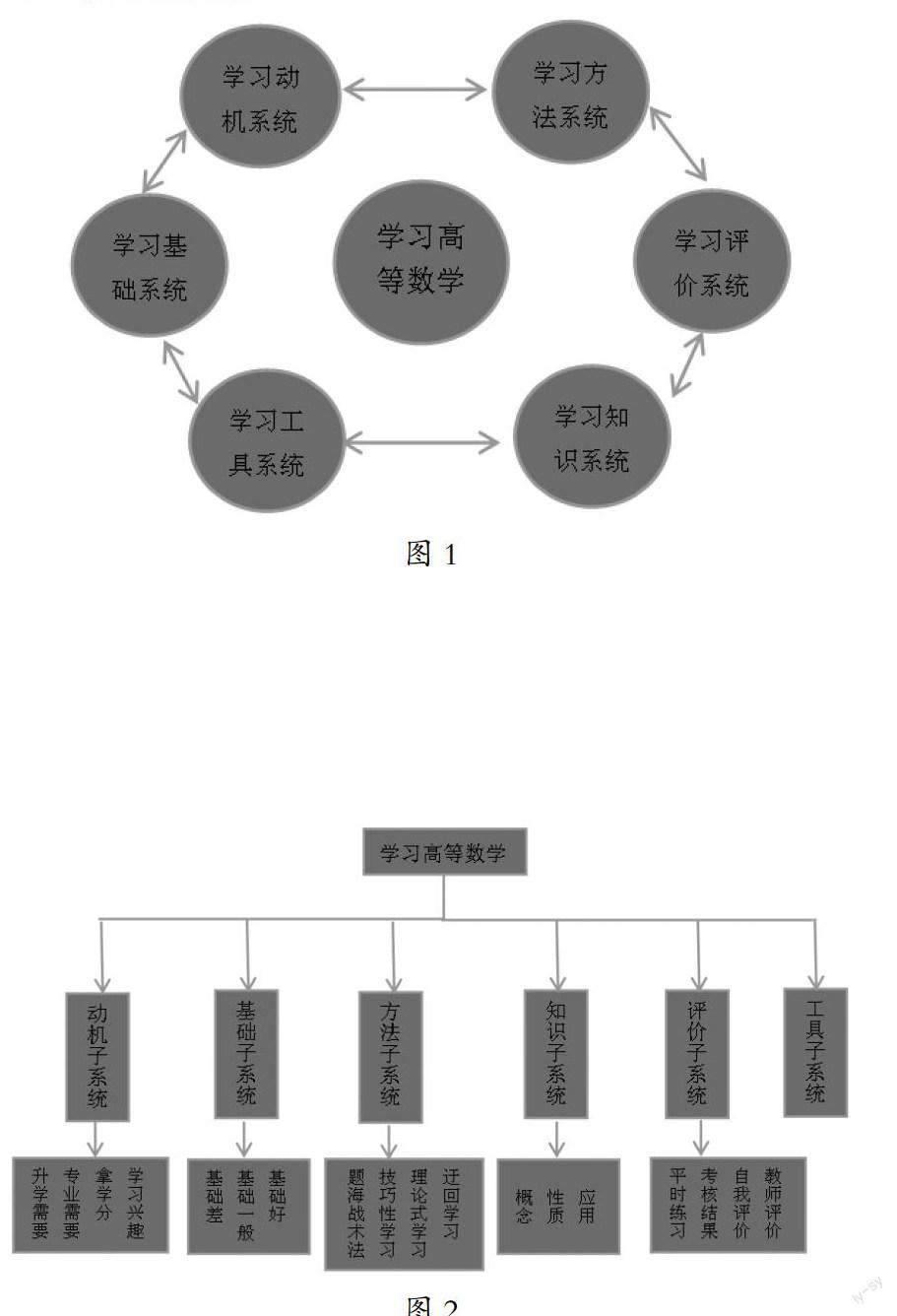
从学习者的角度分析，如果把“学习高等数学”看作一个系统，则可把其划分为“学习者学习动机子系统、自身基础子系统、学习方法子系统、知识子系统、学习工具子系统、评价或效果子系统，这些子系统或组分相互作用构成整个学习系统。[ 3 ]学习者必须弄清自身的学习动机，根据自身的基础特点确定学习方法并选择合适的工具教辅书或学习伙伴，学习吸纳知识，建立自身的知识系统，通过评价及时调整学习方法或树立正确的学习动机，以此提高学习效率或效果，不断优化学习系统。从而提高自身学习的主观能动性和实际应用能力，不断提高学习质量。以下是系统内部结构图1：

如图所示，箭头方向表示子系统之间的作用关系，箭头双向说明各子系统之间的作用关系是双向的。各个子系统之间的相互关系共同构成了“学习高等数学”的有机整体系统。

从学习者的角度分析，下面给出“学习高等数学”系统的结构联系图2。

各个子系统又包含各个要素或组分，以下阐述各个子系统的组成。

1）学习动机系统包括兴趣需求、专业需求、升学需求、拿学分需求等。学习者必须认清自身学习高等数学的目的，才能做出正确的学习选择和学习评价。学习需求因人而异，有的出于学习兴趣；有的仅仅为了拿学分毕业；有的则是因为专业学习的要求，如工程计算相关专业；也有的学习者是为了专插本或考取研究生，再有学习者出于多个学习需求。该子系统也可称为“学习高等数学”的目标系统。

2）学习基础子系统包括基础好、基础一般、基础差三个要素。该子系统与其他子系统间均相互联系、相互影响，它们之间存在直接联系或间接联系。例如：基础好的学习者的学习动机倾向于升学需求或兴趣需求，基础差的則趋于拿学分毕业。反过来，不同的学习动机影响学习者的学习态度和方法，进一步影响学习者的知识结构子系统和评价效果子系统，最后又对学习者的学习基础产生影响，使各子系统间形成作用闭环。

3）学习知识子系统包括概念、性质、应用三大组分。概念组分包括极限、导数、极值、不定积分、定积分等概念；另一方面，每个概念对应的性质，如导数的几何意义；每个概念的实际应用，如不定积分在经济学中的应用等。学习者知识系统的丰富程度取决于其对各项知识的掌握程度，通过对知识点的消化理解，进而总结归纳出知识要点。知识系统也可理解为知识模块，各个模块之间相互关联，相互补充。总之，学习应该是一个“由薄到厚再由厚到薄”的过程，前阶段注重知识的积累，后阶段强调对知识的归纳、理解及应用。

4）学习评价或效果子系统包括学习者平时练习的情况、学习考核结果、学习者自我评价、其他学习者的评价、教师评价。评价目的不在于证明，而在于改进学习高等数学系统。因为评价结果输出后形成反馈信息输入，学习方法子系统、学习动机子系统或学习工具子系统等子系统收到信息后必定作出系统调整，不断改善和优化学习方法，所以评价子系统直接影响学习者的学习效果，进而影响学习目标子系统。

5）学习方法子系统包括迂回学习法、理论式学习法、技巧性学习法、题海战术法等。

高等数学与中学数学最大的区别在于高数侧重数学理论的理解、应用，中学数学侧重计算和解题的技巧性，故学习者初学高数时无法适应高数的学习内容。无法理解数学概念及其实际应用或者跟后面所学知识的关系，这时可采用迂回学习法。即暂时记下无法理解的内容，继续学习后面的知识并回顾已学知识，达到温故知新，更知故的效果。[ 4 ]

另外，高等数学概念相对枯燥抽象，学习者学习时可采取理论联系实际的方法理解和记忆概念。以导数为例，导数概念是高等数学中最重要的概念之一，它是工程、經济、管理、电子计算机等领域中一种重要的数学计算工具，如经济学中的弹性分析、边际成本分析、边际利润分析、边际产量分析等。所以学习者必须重视理论概念的学习和应用。

6）工具子系统包括各类学习辅导书和学习文具，同时也包括教师和同学。选择不同的辅导书对学习者必定产生不同的作用。

3 举例

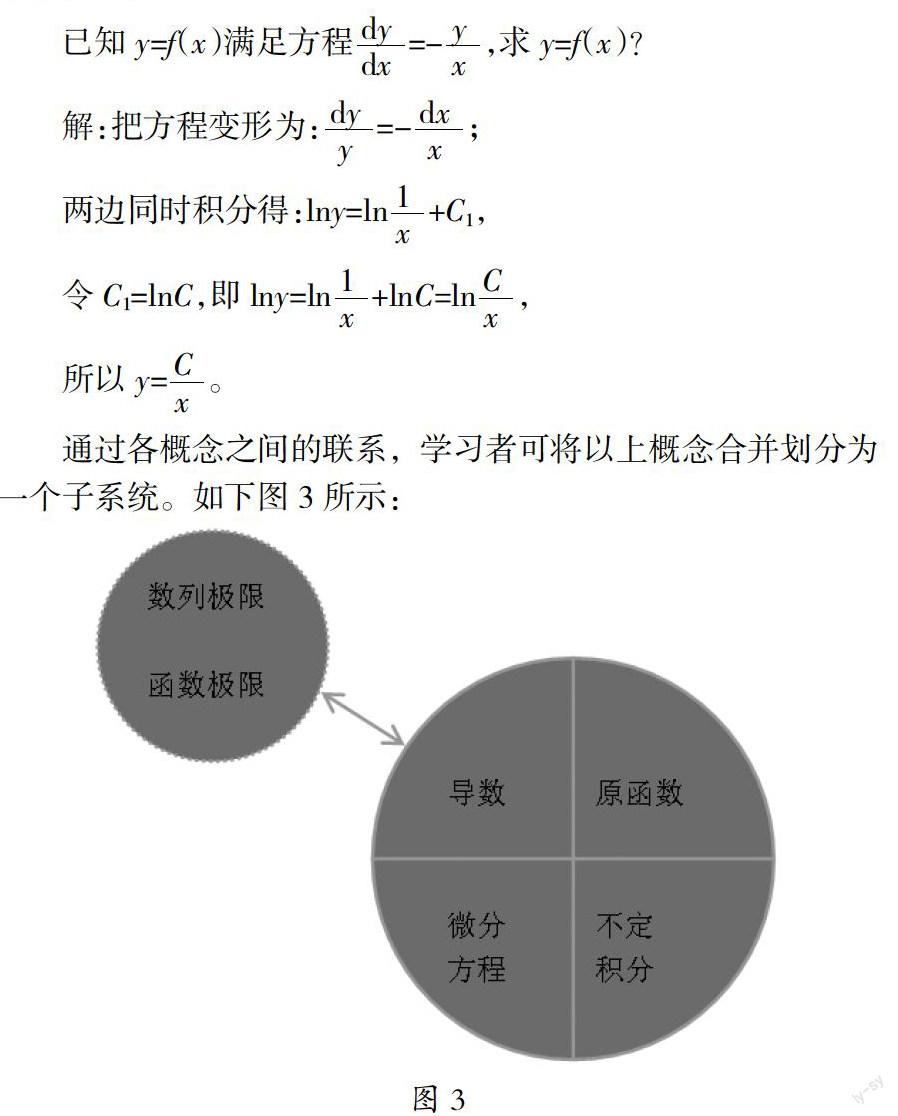
下面以高等数学知识系统的子系统“概念”为例说明。该子系统可再分为若干个主要子系统：数列极限、函数极限、导数、原函数、不定积分、定积分、二重积分、微分方程、常数项级数、函数项级数、幂级数。[ 5 ]

极限概念是高等数学理论体系中最基本的组成部分。由数列xn=f（n）当项数n→∞时极限概念（即“ε-δ语言”）进一步引申出函数y=f（x）在自变量x→∞和x趋于某一点x0时各自的极限定义；再将函数y=f（x）中因变量y对自变量x的平均变化率Δy/Δx在Δx→0时极限值定义为函数y=f（x）在点x0处的导数或微商，记为f ′（x0）或

；紧接着，给出原函数的概念：若在某个区间上有F′（x）=f（x），则称F（x）是f（x）在该区间内的一个原函数；再将f（x）的全体原函数F（x）+C（C为常数）定义为f（x）的不定积分，记为f（x）dx；最后，把联系自变量、函数及其导函数的数学关系式称为微分方程，通过积分逆运算解微分方程，可得出函数y=f（x）；如：

已知y=f（x）满足方程=-，求y=f（x）？

解：把方程变形为：=-；

两边同时积分得：lny=ln+C1，

令C1=lnC，即lny=ln+lnC=ln，

所以y=。

通过各概念之间的联系，学习者可将以上概念合并划分为一个子系统。如下图3所示：

学习者在学习概念的过程中应思考各个知识点之间的多样性、关联性、同一性，对联系较紧密的组分或元素进行合并划分子系统，形成整体思维，不断构建自身的理论体系框架、概念性质联系框架、知识应用结构框架；或者学到一个阶段后温故，回头理解已经学过的概念知识和概念性质以及相应的知识应用点，加深对已学知识的理解的应用并更好的学习理解现阶段学的知识点。

4 结语

文章的目的在于鼓励学习者应用系统理论的思维方法来看待“学习高等数学”这一过程。从不同方面分析“学习高等数学”的结构组成，进而阐述各组分或子系统的组成，并对各子系统的特性进行分析，论述各子系统间的相互作用，最后综合分析，建立“学习高等数学”系统的内部联系网络结构，启示学习者如何学好高等数学，为学习者提供思考的理论路径，旨在达到事半功倍的效果。

参考文献：

[1] 苗东升.论系统思维（一）：把对象作为系统来识物想事[J].系统辩证学学报，2004（07）.

[2] 苗东升.论系统思维（二）：从整体上认识和解决问题[J].系统辩证学学报，2004（10）.

[3] 吴瑞春.用系统科学的观点理解如何上好高中数学课[J].2013（07）.

[4] 余达锦，杨淑玲.创新创业教育背景下高等数学教学方法研究[J].2013（04）.

[5] 郭运瑞.高等数学[M].2014（01）.

[6] 许国志.系统科学[M].2000（01）.

作者简介：郑锐丽（1988.09-），女，广东揭阳人，研究方向：管理系统工程；吴泽宾（1987.10-），男，广东揭阳人，硕士研究生，研究方向：信息系统工程。