低秩张量补全算法综述

刘慧梅，　史加荣

(西安建筑科技大学 理学院， 陕西 西安 710055)



低秩张量补全算法综述

刘慧梅，史加荣

(西安建筑科技大学 理学院， 陕西 西安 710055)

[摘要]随着现代信息技术的快速发展，待分析的数据大都具有很复杂的结构。在获取高维多线性数据的过程中，部分元素可能丢失，低秩张量补全就是根据数据集的低秩性质来恢复出所有丢失元素。低秩张量补全是压缩感知理论的高阶推广，在数学上可以描述为核范数最小化问题。对求解低秩张量补全的核范数最小化模型的现有算法进行了综述。介绍了张量的基础知识和低秩张量补全模型，给出了低秩张量补全的几种主流算法，如：简单低秩张量补全、高精度低秩张量补全以及核心张量核范数的张量补全等，指出了现有低秩张量补全算法中值得研究与改进的方向。

[关键词]张量补全；低秩；核范数最小化；核心张量核范数；交替方向乘子法

随着传感器和存储技术的快速发展，高阶数据分析已经应用到信号处理、计算机视觉和数据挖掘等领域。低秩矩阵补全(Low Rank Matrix Completion，LRMC)和低秩矩阵恢复(Low Rank Matrix Recovery，LRMR)已成为数据分析与处理的研究热点[1-3]，且矩阵秩最小化具有很强的全局约束能力，能很好地刻画出矩阵二维的稀疏性。然而，实际待分析的高维数据往往具有复杂的数据结构，如：彩色图像、视频序列和多光谱图像等。传统的数据表示形式为向量和矩阵，不能很好地刻画这些数据的多线性结构。作为向量和矩阵的高阶推广，张量能够很好地表达高阶数据复杂的本质结构。

实际应用中的高维数据一般具有较低的本征维数，也就是说它们是低秩或近似低秩的。在获取高维数据的过程中，某些元素可能丢失，如何利用已知数据元素的信息来恢复出那些丢失的元素，这个任务被称为低秩张量补全(Low Rank Tensor Completion，LRTC)问题。Liu等人[4]指出LRTC能够充分利用数据所有维的信息，而LRMC仅仅利用数据的两维信息。张量补全现已被成功应用到计算机视觉[4]、EEG[5-6]和超光谱[7-8]等数据的处理中。

近年来，Liu[4,9]和Candy[8]等学者对LRTC算法进行了大量的研究且已取得显著成果。一般而言，对LRTC模型的求解方法主要分为三大类：第一类是把LRMC问题的秩最小化框架扩展延伸到LRTC问题中，即张量低n-秩最小化框架，此方法得到了很多学者的青睐；第二类是应用张量代数的思想来解决LRTC问题，如文献[10-11]提出的Tucker逼近的张量补全算法；第三类是应用流形的思想解决LRTC问题，如Kressner等人[12]提出的张量补全非线性集合CG算法。本文主要对第一类LRTC算法进行综述。

1基本知识

本节介绍一些矩阵与张量代数的基本知识。用大写斜体字母表示矩阵(如：X)，小写字母表示向量(如：x)，用Euclid字母表示张量(如：X)。令X∈RI1×I2×…×IN是一个维数为I1×I2×…×IN的N阶张量，它的(i1，…，iN)元素为xi1…iN，其中I1，…，IN为正整数。

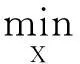
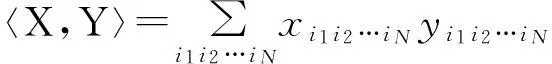
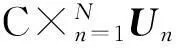
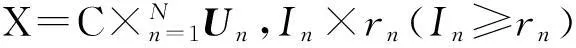
2低秩张量补全模型及算法

2.1问题描述

Liu[4]和Candy[8]等人提出的低秩张量补全模型可表示为下列最优化模型：

(1)

其中rank(X(n))为张量X的n-模式秩，T∈RI1×I2×…×IN，Ω表示采样指标集合。不幸的是，问题(1)是NP难的。由于矩阵核范数是秩函数的凸包络[17]，所以可对模型(1)进行凸松弛，得到张量核范数最小化模型：

(2)

下面综述求解上述张量核范数最小化问题的几种主流算法。

2.2简单低秩张量补全算法

(3)

在模型(3)中，目标函数关于M是可分离的，从而可进一步转化为下面含罚项的优化问题：

(4)

其中λn>0。优化问题(4)是凸的但非光滑，可采用块坐标下降法[19]进行求解：对其中一个块变量进行优化时，固定其余的块变量。因此把最优化问题(4)划分为N+1个子优化问题，并分别进行求解。

当更新X时，固定其它N个块变量，求解下列最优化问题：

(5)

易得此问题的最优解为：

(6)

其中foldn(X(n))表示将矩阵X(n)重新合成张量X。

更新Mn时，需求解下列优化问题：

(7)

简单低秩张量补全算法(Simple Low Rank Tensor Completion，SiLRTC)[4]虽然很容易实现，但是在实际实施过程中会发现它的收敛速度比较慢。

2.3高精度低秩张量补全算法

(8)

模型(8)的增广拉格朗日函数为：

(9)

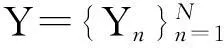
更新M时，对于每个Mn(n=1，2，…，N)有

(10)

更新X时，只需求解如下子优化问题：

(11)

式(11)是一个光滑可微的优化问题，通过一阶最优性条件可得它的最优解：

(12)

这里Ωc为Ω的补集。

Yn的更新： Yn:=Yn-λ(Mn-X)。

惩罚参数λ的更新：λ:=tλ，其中t>1。

高精度低秩张量补全算法(High Accuracy Low Rank Tensor Completion，HALRTC)[4]实质上就是ADMM算法[8]。在实际的应用中，HALRTC收敛速度较快且具有较高的精度。

2.4核心张量核范数的张量补全算法

由定理2可知：当张量X的Tucker分解的模式矩阵Un属于Stiefel流形[16]时，X的核范数与它的核心张量核范数等同。于是最优化问题(2)可转化为：

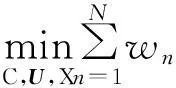
(13)

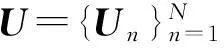
(14)

上式模型的部分增广拉格朗日函数为：

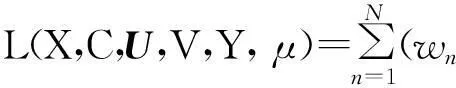
(15)

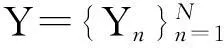
更新V时，对于每个Vn(n=1，2，…，N)有：

(16)

更新C时：

(17)

更新U时，每个Un(n=1，2，…，N)只需通过求解下列优化模型：

其一，PBL教学模式在调动高职院校学生英语口语训练动力与兴趣方面的作用；其二，PBL教学模式在提高学生英语口语表达能力上的作用与具体表现；其三，PBL教学模式在提高学生综合素质方面的作用。

(18)

此模型对应高阶正交迭代(HOOI)分解[21]。通过每次迭代求解式(18)，更新每个Un(n=1，2，…，N)。为了简便，采用非精确迭代策略，即对每个Un仅仅更新一次，则有如下更新公式：

(19)

其中算子SVD(rn,M(n))表示对矩阵M(n)进行奇异值分解后，取其前rn个最大奇异值对应的左奇异向量。

更新X时，需求解下列最优化问题：

(20)

易得到上式(20)的解如下：

(21)

惩罚参数μ的更新规则与HALRTC算法中的λ的更新规则相同。

核心张量核范数的补全(Core Tensor Nuclear Norm Tensor Completion，CNNT)[17]算法是基于经典的张量Tucker分解，并给最优化问题(2)附加一定的条件，使得张量核范数和它的核心张量核范数相等，从而达到降低变量维数的目的。

2.5基于Parafac分解的因子矩阵核范数最小化张量补全算法

模型(2)应用张量的另一经典Parafac分解并松弛得：

(22)

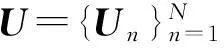
(23)

式(23)的部分增广拉格朗日函数为：

(24)

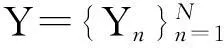
更新M时，对于每个变量Mn(n=1，2，…，N)有：

(25)

更新U时，对于每个Un(n=1，2，…，N)，需求解下列子优化问题：

(26)

在求解(26)时，若A=V1°V2°…°VN，则A(n)=Vn(VN⊙…⊙Vn+1⊙Vn-1⊙…⊙V1)T，此处⊙为Khatri-Rao积[16]。令Bn=(UN⊙…⊙Un+1⊙Un-1⊙…⊙U1)T) ，则优化问题(26)转化为如下形式：

(27)

与CNNT算法相同，采用非精确更新策略，得到Un的闭形式解为：

(28)

其中I为单位矩阵。

更新X时，需求解如下优化问题：

(29)

易得到优化问题(29)的解为：

(30)

惩罚因子μ的更新规则与CNNT算法中的μ更新一致。

基于Parafac分解的因子矩阵核范数最小化张量补全算法(NNCP)[16]对张量的Parafac分解要求很高，所以并不适用于任一低秩张量补全模型。但是总的来说，这种模型可以降低时间复杂度。

2.6矩阵分解的张量补全算法

对于最优化问题(2)，给出相应矩阵分解的张量补全优化模型[16,20]：

(31)

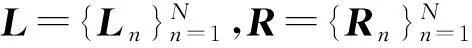
(32)

更新变量L和R时，对于每个Ln和Rn(n=1，2，…，N)，分别解下列子优化问题：

(33)

(34)

通过解式(33)和(34)得变量Ln和Rn的闭形式解：

(35)

其中QR(·)表示对矩阵进行QR分解。

更新变量X时，需求解

(36)

通过式(36)的一阶最优化条件，易得如下式的闭形式解：

(37)

矩阵分解的张量补全(Matrix Factorization Method for Tensor Completion，MFTC)[16]算法与前面综述的CNNT算法和NNCP算法的目的都是为了降低计算复杂度。此算法不管是在精度上还是运行时间上都有明显的优越性。

上述几种低秩张量补全算法主要通过秩极小化的框架来求解优化问题(2)。当然，除了前面我们综述的这几种算法外，还有其它算法值得关注，如：Shi等人[22]为了降低低秩张量补全算法的时间复杂度而提出基于Tuker分解的低秩张量补全算法，此算法通过采用瘦的QR分解来替代奇异值分解达到降低计算复杂度的目的；Kressner等人[12]提出基于黎曼流形的非线性集合CG算法，减少了大规模的奇异值的分解；Candy等人[8]提出基于Douglas-Rachford分离技术的张量补全算法，此算法考虑了噪声的存在。由于篇幅问题，我们不再一一赘述。

3结束语

本文综述了低秩张量补全模型的几种求解算法，并评价了这些算法优缺点。当前，对LRTC的研究不管是在理论和算法上，还是在实际应用上都处于初步研究阶段。因此，对低秩张量补全算法的研究仍将是一个热点。下面列出的几方面在今后的研究中还需值得关注：(1)张量秩的上界估计，许多算法对于张量秩的上界的估计都是依经验给出，而如何使秩自学习给出是值得我们深究的；(2)低秩张量补全算法的求解基本上都需要计算每一模式展开的SVD，这项工作的计算复杂度是极其大的，如何降低这一计算复杂度的工作仍需努力；(3)现有算法基本上都地在假设不存在噪声的情况下提出的，考虑数据中存在噪声的低秩张量补全算法较少。

[参考文献]

[1]CANDèS E J，LI Xiao-dong，MA Yi，et al.Robust principal component analysis？[J].Journal of ACM，2011，58(3)：1-37.

[2]CANDèS E J，RECHT B.Exact matrix completion via convex optimization[J].Foundations of Computational Mathematics，2008，9(6)：717-772.

[3]KESHAVAN R H，MONTANARI A.Matrix completion from noisy entries[J].Journal of Machine Learning Research，2010，11(3)：2057-2078.

[4]LIU Ji，MUSIALSKI P，WONKA P，et al.Tensor completion for estimating missing values in visual data[J].IEEE Translations on Pattern Analysis and Machine Intelligence，2013，35(1)：208-220.

[5]ACAR E，DUNLAVY D M，KOLDA T，et al.Scalable tensor factorization for incomplete data[J].Chemometrics and Intelligent Laboratory Systems，2011，106(1)：41-56.

[6]MØRUP M，HANSEN L K，HERRMANN C S，et al.Parallel factor analysis as an exploratory tool for wavelet transformed event-relatedEEG[J].NeuroImage，2006，29(3)：938-947.

[7]SIGNORETTO M，PLAS R，MOOR B，et al.Tensor versus matrix completion：a comparison with application to spectral data[J].IEEE Signal Processing Letters，2011，18(7)：403-406.

[8]GANDY S，RECHT B，YAMADAI.Tensor completion and low-n-rank tensor recovery via convex optimization[J].Inverse Problem，2011，27(2)：25-43.

[9]LIU Ji，LIU Jun，WONKA P，et al.Sparse non-negative tensor factorization using columwise coordinate decent[J].Pattern Recognition，2012，45(1)：649-656.

[10]史加荣，焦李成，尚凡华.张量补全算法及其在人脸识别中的应用[J].模式识别与人工智能，2011，24(2)：255-261.

[11]史加荣.多尺度张量逼近及应用[D].西安：西安电子科技大学，2012.

[12]KRESSNER D，STEINLECHNER M，VANDEREYCKEN B.Low-rank tensor completion by Riemannian optimization[J].BIT Numerical Mathematics，2014，54(2)：447-468.

[13]CAI Jian-feng，CANDèS E J，SHIN Zuo-wei.A singular value thresholding algorithm for matrix completion[J].Siam Journal on Optimization，2010，20(4)：1956-1982.

[14]KOLDA T G，BADER B W.Tensor decompositions and applications[J].Siam Review，2009，51(3)：455-500.

[15]KOLDA T G，GIBSON T.Multilinear operators for higher order decompositions[R].Albuquerque：Sandia National Laboratories，2006.

[16]刘圆圆.快速低秩矩阵与张量恢复的算法研究[D].西安：西安电子科技大学，2013.

[17]FAZEL M.Matrix rank minimization with applications[DJ].Palo Alto：Stanford University，2002.

[18]TSENG P.Convergence of block coordinate descent method for nondifferentiable minimization[J].Optimization Theory Application，2001，109(3)：475-494.

[19]IN Zhou-chen，CHEN Min-ming，MA Yi.The augmented lagrange multiplier method for exact recovery of corrupted low-rank matrices[R].Urbana-Champaign：University of Illinois at Urbana-Champaign，2009.

[20]LIU Yuan-yuan，JIAO L C，SHANG Fan-hua. A fast tri-factorization method for low-rank matrix recovery and completion[J].Pattern Recognition，2013，46(1)：163-173.

[21]SHEEHAN B N，SAAD Y.Higher order orthogonal iteration of tensors (HOOI) and its relation to PCA and GLRAM[C].Proceedings of the Seventh SIAM International Conference on Data Mining，2007：355-365.

[22]SHI Jia-rong，YANG Wei，YONG Long-quan，et al.Low-rank tensor completion via tucker decompositions[J].Journal of Computational Information Systems，2015，11(10)：3759-3768.

[23]CHEN Cai-hua，HE Bing-sheng，YUAN Xiao-ming.Matrix completion via an alternating direction method[J].Ima Journal of Numerical Analysis，2012，32(1)：227-245.

[24]CANDèS E J，TAO T.The power of convex relaxation：near optimal matrix completion[J]. IEEE Transactions on Information Theory，2009，56(5)：2053-2080.

[25]LIU Yuan-yuan，JIAO L C，SHANG Fan-hua.An efficient matrix factorization based low-rank representation for subspace clustering[J].Pattern Recognition，2013，46(1)：284-282.

[26]HILLAR C J，LIM L H.Most tensor problems are NP-hard[J].CORR，2009，60(6)：1333-1360.

[27]GENG Juan，WANG Lai-sheng，XU Yi-tian，et al.A weighted nuclear norm method for tensor completion[J].International Journal of Signal Processing Image Processing and Pattern Recognition，2014，7(1)：1-12.

[28]MØRUP M.Applications of tensors (multiway array) factorizations and decompositions in data mining[J].Wiley Interdisciplinary Reviews：Data Ming and Knowledge Discovery，2011，1(1)：24-40.

[责任编辑：谢 平]

Survey on algorithms to low-rank tensor completion

LIU Hui-Mei,SHI Jia-Rong

(School of Science, Xi’an University of Architecture and Technology, Xi’an 710055, China)

Abstract:With the fast development of modern information technology, most data to be analyzed have very complex structures. In the process of high-dimensional multi-linear data acquisition, some elements may be lost. Low Rank Tensor Completion (LRTC) is just a technique to recover all missing elements by the low rank property of the investigated data. LRTC is the higher-order generalization of compressed sensing and is mathematically described as a nuclear norm minimization problem. This paper reviews the existing algorithms to LRTC. First, preliminaries on tensor algebra and models of LRTC are briefly introduced. Then this paper reviews several mainstream algorithms to LRTC including simple low-rank tensor completion, high accuracy low-rank tensor completion, core tensor nuclear norm of tensor completion and so on. Finally, the paper points out the research directions of LRTC needed to be investigated and improved.

Key words:tensor completion；low rank；nuclear norm minimization；core tensor nuclear norm；alternating direction method of multipliers

[中图分类号]TP391

[文献标识码]A

作者简介：刘慧梅(1989—),女，陕西省延安市人，西安建筑科技大学硕士研究生，主要研究方向为概率统计应用；[通信作者]史加荣(1979—)，男，山东省聊城市人，西安建筑科技大学副教授，博士，主要研究方向为机器学习与模式识别。

基金项目：国家自然科学基金资助项目(61403298)；陕西省自然科学基础研究计划项目(2014JQ8323)

收稿日期：2015-12-02修回日期：2016-02-25

[文章编号]1673-2944(2016)02-0080-07