例谈初中数学几何综合问题的解题方法

郑波

摘 要： 初中数学中的几何问题不仅是平时教学中的重点，而且是中考中必考的知识点，在中考中它往往以压轴题出现，因此，在平时的教学中我们要关注这类题.本文从作者的教学实践出发，结合具体的中考实例谈谈初中数学几何综合问题的解题方法，其中主要包括从特殊到一般的解题方法和根据题干建立联系的方法.

关键词： 初中数学 几何综合题 解题方法 类型

几何综合题常常和运动问题结合起来，在题设图形中存在一个或多个动点，甚至是一个图形，它们在线段、射线或弧线上运动的一类开放性题目.解决这类问题的关键是动中求静，灵活运用有关数学知识，如平移、旋转、对称和运动过程中的面积变化关系等解决问题.在加入运动问题的同时，几何综合问题又可以大致分为两类，一类是几何综合题，一类是代数和几何型综合题.这两类题目不仅有各自的特点，还有一些共同点，下面笔者一一分析、阐述.

类型一：几何综合题

1.概念分析

几何型综合题是指以几何知识为主或以几何变换为主的一类综合题，涉及知识主要包括几何的定义、公理、定理及几何变换等内容.

2.解题策略

解决几何型综合题的关键是把代数知识与几何图形的性质及计算与证明有机融合起来，进行分析、推理，从而达到解决问题的目的.概括来讲就是采用从特殊到一般的解题方法.

3.例题展示

（2015·湖州）已知在△ABC中，AB边上的动点D由A向B运动（与A，B不重合），点E与点D同时出发，由点C沿BC的延长线方向运动（E不与C重合），连接DE交AC于点F，点H是线段AF上一点.

（1）初步尝试

如图1，若△ABC是等边三角形，DH⊥AC，且点D，E的运动速度相等.求证：HF=AH+CF.

小王同学发现可以由以下两种思路解决此问题：

思路一：过点D作DG∥BC，交AC于点G，先证GH=AH，再证GF=CF，从而证得结论成立；

思路二：过点E作EM⊥AC，交AC的延长线于点M，先证CM=AH，再证HF=MF，从而证得结论成立.

请你任选一种思路，完整地书写本小题的证明过程.

（2）类比探究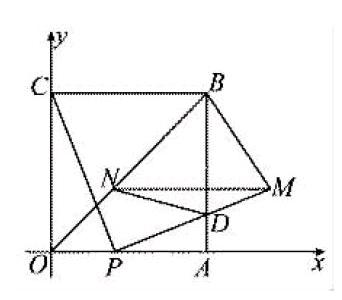

（3）延伸拓展

4.例题分析

类型二：代数和几何型综合题

1.概念分析

代数和几何型综合题是指以代数知识与几何知识综合运用为主，包括坐标系中的图形变换等的一类综合题，涉及知识以函数与圆、方程，函数与三角形、四边形等相关知识为主.

2.解题策略

几何图形形象直观，解题过程的可操作性强，因此解决这类题目时可以采用数形结合的思想.概括来讲就是根据题干建立适当联系.

3.例题展示

（2015·衡阳）如图，四边形OABC是边长为4的正方形，点P为OA边上任意一点（与点O，A不重合），连接CP，过点P作PM⊥CP交AB于点D，且PM=CP，过点M作MN∥OA，交BO于点N，连接ND，BM，设OP=t.

（1）求点M的坐标（用含t的代数式表示）；

（2）试判断线段MN的长度是否随点P的位置的变化而改变？并说明理由；

（3）当t为何值时，四边形BNDM的面积最小？

结语

纵观以上分析，我们发现要想掌握好几何综合性问题，不仅要将课本基本知识熟记于心，还要掌握一定的思想方法，比如：分类讨论思想、函数思想、方程思想、数形结合思想和转化思想等，在掌握这些内容后，还要把握“运动”的要义，不管是点的运动、线的运动、面的运动，都要熟悉，只有这样才能在考试中取得好成绩.

参考文献：

[1]王义兵.浅谈初中数学中函数与几何的综合应用问题[J].中学数学，2012，24.

[2]李长军，徐毅.解析几何学习中应注意的几个问题[J].数学通报，2005，08.

[3]张宏政.代数与几何综合问题[J].中学生数理化（初中版，中考版），2009，06.