Abundance of Asymmetric Dark Matter in Brane World Cosmology∗

Haximjan Abdusattar and Hoernisa Iminniyaz

School of Physics Science and Technology,Xinjiang University,Urumqi 830046,China

1 Introduction

Recent analyses show the possibility that the Dark Matter can be asymmetric.Most recent papers discussed the asymmetric Dark Matter models.[1−2]The motivation for considering this scenario is the comparable average density of Baryon and Dark Matter which is ΩDM=5Ωbwith Ωb≈0.046.Generally neutral,long-lived or stable Weakly Interacting Massive Particles(WIMPs)are assumed to be good Dark Matter candidates.One example is the neutralino which is stable particle with R-parity introduced in supersymmetry.Neutralino is Majorana particle for which its particle and anti-particle are the same.However,until now there is no evidence which shows that the Dark Matter particles should be Majorana particle.In the universe,most of the known elementary particles are not Majorana particles.The particles and anti-particles are distinct from each other if particles are fermionic.Therefore it is legitimate to consider the possibility that the Dark Matter particles can be asymmetric for which particles and anti-particles are not identical.

In Refs.[3–4],the authors investigated the relic abundance of asymmetric Dark Matter particles in the standard cosmological scenario in which particles were in thermal equilibrium in the early universe and decoupled when they were non-relativistic.There is an assumption that the Dark Matter asymmetry is created well before Dark Matter annihilation reactions freeze-out and in the beginning there are more particles than the anti-particles.In the standard cosmological scenario,it is assumed the particles and anti-particles are annihilated away when the asymmetry is large enough.Therefore the relic density for anti-particles is depressed in the present universe.There is only particles.Thus the asymmetric Dark Matter is only assumed to be detected by direct detection.

In nonstandard cosmological scenarios like quintessence,scalar-tensor models,brane world cosmological scenarios,the Hubble expansion rate is increased.[5−8]The modified Hubble expansion rate affects the relic density of asymmetric Dark Matter.The asymmetric Dark Matter relic density is already investigated in such models including quintessence model,scalar-tensor model.[9−11]In quintessence model,scalar-tensor models,the relic densities of both particles and anti-particles are increased simultaneously due to the increased Hubble expansion rate.The relic density of anti-particle is not depressed for appropriate annihilation cross section for nonstandard cosmological scenarios.This leaves the possibility that the asymmetric Dark Matter can be detected by indirect detection.

Recently Meehanet al.[12]probed the relic density of asymmetric Dark Matter in brane world cosmology.They found the enhanced Hubble expansion rate in brane world cosmology leads to the earlier decay of the particle and anti-particle from the equilibrium.Therefore there are enhanced relic densities for both particles and anti-particles.In our work we give more detailed analysis of the relic density of asymmetric Dark Matter in brane world cosmology in different way.We closely follow the analytic solution of asymmetric Dark Matter in standard cosmological scenario and derive the analytic solution of the relic density of asymmetric Dark Matter in brane world cosmological model.

The paper is arranged as follows.In Sec.2,the asymmetric Dark Matter relic density is calculated numerically and analytically in brane world cosmology.In Sec.3,we find the constraints on the parameter space of brane world cosmology from the observational data.The fi nal section is devoted to the conclusions.

2 Relic Abundance of Asymmetric Dark Matter in Brane World Cosmology

In this section,we calculate the relic abundance of asymmetric Dark Matter in brane world cosmological scenario.Before starting the calculation let us briefly review the brane world cosmological scenario.In brane world cosmology,the Hubble expansion rate is derived as[13]

whereGis 4-dimensional Newton coupling constant andρis the energy density of the ordinary matter on the brane withσbeing the brane tension.Ris the scale factor andkis the curvature of the 3-dimensional space.FinallyC′is a constant of integration which is known as dark radiation.We setk=C′=0 in this analysis and insertρ=π2/30g∗T4andσ=6into above equation whereM5is the 5-dimensional Plank mass andMPlis the reduced Planck massGeV.Then one obtains

wherex=mχ/Twithmχbeing the mass of Dark Matter particles andkb=(360M).Hereg∗is the effective number of the relativistic degrees of freedom.In order not to con fl ict with Big Bang Nucleosyn thesis(BBN)when temperatureT=1 MeV,the second term in the square rootkb/x4→1.This imposes thatM5>1.2×104GeV.Hstdis the Hubble expansion rate in the standard cosmological scenario,

Following we write down the Boltzmann equation with the modified expansion rate in brane world cosmology,which is the main equation to find the relic density for Dark Matter.In our analysis,Dark Matter particle is denoted asχ,which is not self-conjugate,i.e.the anti-particleThe Boltzmann equations for particle and anti-particle are

Here it is assumed that onlyχpairs can annihilate into Standard Model(SM)particles,whileχχandpairs can not.are the number densities of particle and anti-particle.is the thermally averaged annihilation cross section multiplied with the relative velocity of the two annihilatingχ,particles.are the equilibrium number densities ofχand,here it is assumed the Dark Matter particles were non-relativistic at decoupling.The equilibrium number densitiesandare given by

wheregχis the number of the intrinsic degrees of freedom of the particles andµχ,are the chemical potential of the particle and anti-particle,=−µχin equilibrium.

The number densities for particle and anti-particle are obtained by solving the Boltzmann equations(4).To solve the Boltzmann equations(4)in brane world cosmology,we follow the standard picture of Dark Matter evolution.[4,14]It is assumed the particlesχandwere in thermal equilibrium at high temperature.The equilibrium number densities decrease exponentially when temperature drops below the mass of the particle,formχ>|µχ|.Finally the falls of the interaction rates Γ =nχfor particle andfor anti-particle below the Hubble expansion rateHlead to the decoupling of the particles and antiparticles from the equilibrium.The number densities of the particles and anti-particles in a co-moving space are almost constant from the decoupling point.The temperature at that point is called freeze-out temperature.

First,we rewrite the Boltzmann equations(4)in terms of dimensionless new quantitiesandx=mχ/T.The entropy density is given bys=(2π2/45)g∗T3.During the radiation dominated period,we assume that the universe expands adiabatically,then the Boltzmann equations(4)become

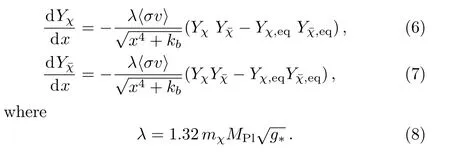
From Eqs.(6)and(7),we obtain

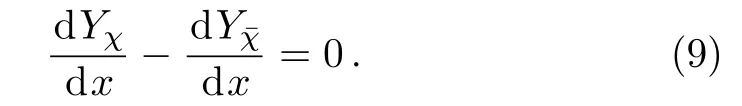
This implies

whereCis the difference of the co-moving densities of the particles and anti-particles and it is conserved.Using Eq.(10),the Boltzmann equations(6)and(7)become

whereMostly we use the WIMP annihilation cross section,which is expanded in the relative velocityvbetween the annihilating WIMPs.Its thermal average is

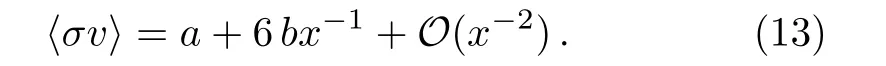
Hereais the dominant contribution toσvwhen particle and anti-particle are in ans-wave for the limitv→0.bis thep-wave contribution toσvwhen thes-wave annihilation is suppressed.

Fig.1(Color online)The relic abundances Yχand Y¯χfor particle and anti-particle as a function of the inversescaled temperature x for C=4×10−12,mχ =100 GeV,gχ =2,g∗=90,a=1.31×10−25cm ·s−1,b=0 for panels(a),(c),(e)and a=1.38×10−24cm3·s−1,b=0 for panels(b),(d),(f);M5=5×105GeV in(a),(b);M5=106GeV in(c),(d)and M5=5×106GeV in(e),(f).

Figure 1 shows the relic abundanceYχ,χ¯evolution as a function of the inverse-scaled temperaturexfor particle and anti-particle for different cross sections andM5in brane cosmology scenario and standard scenario.This figure is plotted using the numerical solutions of Eqs.(11)and(12).Here we takeC=4×10−12,mχ=100 GeV,gχ=2,g∗=90,a=1.31×10−25cm3·s−1,b=0 for panels(a),(c),(e)anda=1.38×10−24cm3·s−1,b=0 for panels(b),(d),(f);M5=5×105GeV in(a),(b);M5=106GeV in(c),(d)andM5=5×106GeV in(e),(f).The dot-dashed(red)line is the particle abundanceYχ,band the thick(red)line is the anti-particle abundancein brane world cosmology;the dashed(blue)line is particle abundanceYχ,sand dotted(blue)line is the anti-particle abundancein the standard scenario.

The double dotted(black)line is the equilibrium valueof the anti-particle abundance.Hubble expansion rate in brane world cosmology is larger than the Hubble expansion rate in the standard case.Particles and antiparticles freeze-out earlier than the standard cosmology.After decay of thermal equilibrium,there are more particles and anti-particles left in brane world cosmology than the standard case for appropriate cross section.Of course the extent of the increase depends on the cross sections and 5-dimensional Planck mass scaleM5.The relic abundancesYχ,bfor particleχandfor anti-particleare larger than the standard case for panels(a)and(c)when the cross section isa=1.31×10−25cm3·s−1for differentM5.We found for the same cross section the increase is larger for smallerM5.WhenM5=5×106GeV in panel(e),the relic abundances for particle and anti-particle in brane world cosmology are almost same with the standard result.There is no enhancement for the relic density for particles and anti-particles.On the other hand,in brane world cosmology,for the larger cross section asa=1.38×10−24cm3·s−1the particle abundance is almost kept in the same amount with the particle abundance in standard cosmology for different scaledM5.This is shown in panels(b),(d)and(f).The anti-particle abundance is depressed for such kind of large cross section.It is more obvious for largerM5as in panel(f).

Using the same method as Refs.[4,9,11],we obtain the analytic solution of the relic density for asymmetric Dark Matter in brane world cosmology.We solve Eq.(12)fordensity first and then use the relationYχ−=Cto findYχeasily.The Boltzmann equation(12)is rewritten as:

where∆¯χ=−Y¯χ,eq.We consider two extreme cases.At high temperature,closely tracks its equilibrium valuevery well.is small,then we can neglect dandThe Boltzmann equation(14)then becomes

Repeating the same way as in Refs.[4,9,11],one obtains the solution for

This solution is used to determine the freeze-out temperaturefor

In the second case,the production term∝can be ignored in the Boltzmann equation(14)for sufficiently low temperature,i.e.forx>therefore

After integration of Eq.(17)fromto∞,we obtain the fi nal WIMP abundance.Here the integration range is divided into two parts:one part is fromtoxtwhere the brane world cosmology is applied.At the transition temperaturext,the standard cosmology is recovered.It is given byxt=mχ/(0.51×10−9GeV).[7]Second part is fromxtto∞in which the standard cosmology is used.Again assuming∆χ()≫∆χ(∞),we have

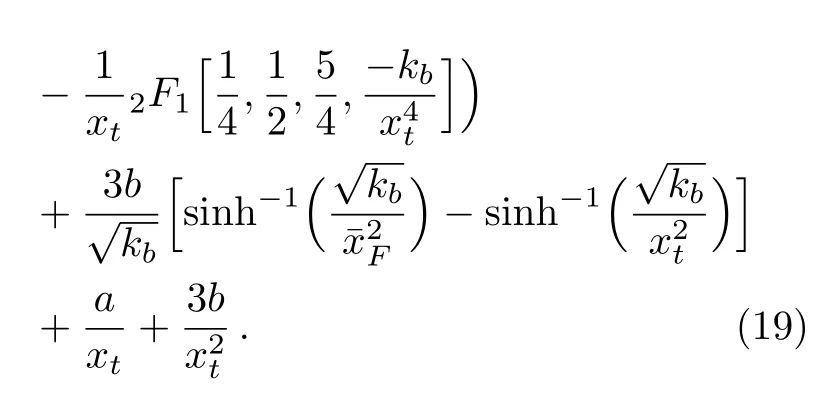
Using Eq.(10),we obtain the relic abundance forχparticle,

WhenxF=,Eqs.(18)and(20)are consistent with the constraint(10).Usually the fi nal abundance is expressed as

heres0=2.9×103cm−3is the present entropy density,andρcrit=is the critical density.The prediction for the present relic density for Dark Matter is then given by

The freeze-out temperature for¯χis fixed using the standard method.It is assumed that the deviation∆¯χis of the same order of the equilibrium value ofY¯χ:

whereξis a numerical constant of order unity.We find the approximate analytic result matches with the exact numerical result very well when we choose

3 Constraints on Parameter Space

The present cold Dark Matter relic density is given as

by Planck 2015 data,[15]whereh= 0.673±0.098 is the present Hubble expansion rate in units of 100 km·s−1·Mpc−1.We use this result to find the constraints on the parameters in brane world cosmology for asymmetric Dark Matter.The total Dark Matter density is

Figure 2 shows the relation between the cross section parametersa,band asymmetry factorCfor the brane world cosmology and standard cosmology when the Dark Matter relic density ΩDMh2=0.1199. Here we takemχ=100 GeV,gχ=2 andg∗=90,M5=106GeV.The dashed(red)lines are for the standard cosmology and the thick(blue)lines are for the brane world cosmological scenario.WhenCis small asC=0 toC=3.5×10−12,the cross section is almost independent ofC.The reason is that for smallC,the formulae forEq.(18)andEq.(22)can be recovered to the result for symmetric Dark Matter in standard cosmology.When the asymmetryCis large,e.g.C=4.0×10−12,the particle and anti-particle are completely annihilated away and the relic density is independent of the cross section.On the other hand,for brane world cosmology,the cross section is larger than the standard cosmology for the observed value of Dark Matter.The reason is that in brane world cosmological scenario the interaction rate is larger than the standard scenario.Asymmetric Dark Matter particles need larger annihilation cross sections in order to fall in the observation range.In Fig.2(a),it is shown fors-wave annihilation cross sections froma=3.99×10−26cm3·s−1toa=8.50×10−23cm3·s−1,the observed Dark Matter abundance is obtained forC=0 to 4.3×10−12.It is for the standard cosmology.The initial cross-section is increased toa=1.93×10−25cm3·s−1for the brane world cosmology.The similar behavior is seen in Fig.2(b).The cross section is increased evidently for brane world cosmology for boths-wave annihilation andp-wave annihilation cross sections to obtain the observed Dark Matter abundance.

For asymmetric Dark Matter,since in the beginning it is assumed that there is less anti-particle than the particle and at late time the anti-particle is completely annihilated away with the particle.Therefore the rest is the particle,which made up the present total Dark Matter abundance in asymmetric Dark Matter case in standard cosmological scenario.Thus the asymmetric Dark Matter particle is supposed to be detected by direct detection.Usually the indirect detection is not available for the asymmetric Dark Matter.However,for asymmetric Dark Matter in nonstandard cosmological scenarios including quintessence,scalar-tensor model and brane world cosmology,[9−11]the relic densities for both particle and anti-particle are increased due to the enhanced Hubble expansion rate.Again for appropriate cross section,the relic densities for both particle and anti-particle are almost in the same amount,which is different from the standard cosmological scenario where the anti-particle relic density is depressed.Therefore the indirect detection is possible for nonstandard cosmology.However,for large annihilation cross section asa=1.38×10−24cm3·s−1,the indirect detection signal can not be used.In Fig.1,it is shown when the cross section is as large asa=1.38×10−24cm3·s−1,the relic abundance of anti-particle is suppressed.Therefore there is not enough anti-particle left,which can annihilate with particle to make up the indirect detection signal.Thus the indirect detection for asymmetric Dark Matter is available in conditionally where the annihilation cross section is not so large.As we showed in Fig.1,it depends on the scale ofM5,the mass of Dark Mattermχ,and most important is the cross section.In this article,it is assumed there is only particle and anti-particle annihilations.Therefore the abundant Dark Matter particle can not annihilate with itself to make the product particle,which can be detected by indirect detection experiments.

Fig.2 (Color online)The allowed region in the(a,C)plane for b=0(a),and(b,C)plane for a=0(b)when the Dark Matter density Ωh2=0.1199.Here we take mχ =100 GeV,gχ =2 and g∗ =90,M5=106GeV.The dashed(red)line is for standard cosmology and the thick(blue)line is for brane world cosmology.

Fig.3 (Color online)Ratio of the relic abundance of anti-particle and particle as a function of annihilation cross section a in brane world cosmology and in the standard cosmology for the asymmetry factor C=4×10−12.The dotted(black)line is for the asymmetric Dark Matter(ADM)in standard cosmology and the solid(red)line is for the asymmetric Dark Matter in brane world cosmology.Here b=0,mχ=100 GeV and C=4×10−12,M5=106GeV,gχ =2,g∗ =90.

The ratio of the relic abundance of the anti-particle to the particle as a function of the annihilation cross sectionais plotted in Fig.3 forC=4×10−12.Here the dotted(black)line for asymmetric Dark Matter in standard cosmology and the solid(red)line in brane world cosmology.The decrease of the ratio is slower for brane world cosmology comparing to the standard cosmology as the cross section increases.For example,for the cross section valuea=2.50×10−25cm3·s−1,the ratio is decreased to 2.2×10−5for standard cosmology and 8.6×10−2for brane world cosmology.We noticed that when the cross section increases,in both cases the abundances of antiparticles are suppressed.Therefore the indirect detection signal is not used for too large cross section in brane world cosmology for asymmetric Dark Matter.

4 Summary and Conclusions

In this paper we investigated the relic abundance of asymmetric WIMP Dark Matter in brane world cosmology.For asymmetric Dark Matter the particles and antiparticles are different from each other.It is assumed the asymmetry starts well before the epoch of thermal decoupling of the WIMPs.The asymmetric Dark Matter particles and anti-particles freeze-out earlier than the standard cosmology due to the enhanced Hubble rate in brane world cosmology.This leads to the increase of the relic density of asymmetric Dark Matter particles.

We found that the relic densities of both particles and anti–particles are increased in brane world cosmology.The size of the increase depends on the 5-dimensional Planck mass scaleM5and the cross sections.The increases are more sizable for smallerM5for the same cross section.WhenM5is large,e.g.M5=5×106GeV,the case in the standard cosmology is recovered.For larger annihilation cross section asa=1.38×10−24cm3·s−1,the particle abundance in brane world cosmology is the same with the particle abundance in standard cosmology for differentM5.The antiparticle abundance is suppressed.

We used the Planck 2015 data to give the constraints on the cross section and asymmetry factorCin brane world cosmology.We showed that the indirect detection signal is used for asymmetric Dark Matter in brane world cosmology for not large annihilation cross section.

The result which is obtained in our work is important to understand the relic abundance of asymmetric Dark Matter in the early universe before Big Bang Nucleosyn thesis.If we know the annihilation cross section in the brane world cosmology,we can find the relic density of Dark Matter in this scenario.It has important effect to investigate the early universe before BBN.

[1]S.Nussinov,Phys.Lett.B 165(1985)55;K.Griest and D.Seckel,Nucl.Phys.B 283(1987)681;R.S.Chivukula and T.P.Walker,Nucl.Phys.B 329(1990)445;D.B.Kaplan,Phys.Rev.Lett.68(1992)742;D.Hooper,J.March-Russell,and S.M.West,Phys.Lett.B 605(2005)228;[arXiv:hep-ph/0410114];J.Cosmol.Astropart.Phys.0901(2009)043,[arXiv:0811.4153v1[hepph]];H.An,S.L.Chen,R.N.Mohapatra,and Y.Zhang,J.High Energy Phys.1003(2010)124,[arXiv:0911.4463[hep-ph]];T.Cohen and K.M.Zurek,Phys.Rev.Lett.104(2010)101301,[arXiv:0909.2035[hep-ph]];D.E.Kaplan,M.A.Luty,and K.M.Zurek,Phys.Rev.D 79(2009)115016,[arXiv:0901.4117[hep-ph]];T.Cohen,D.J.Phalen,A.Pierce,and K.M.Zurek,Phys.Rev.D 82(2010)056001,[arXiv:1005.1655[hep-ph]];J.Shelton and K.M.Zurek,Phys.Rev.D 82(2010)123512,[arXiv:1008.1997[hep-ph]].

[2]A.Belyaev,M.T.Frandsen,F.Sannino,and S.Sarkar,Phys.Rev.D 83(2011)015007,[arXiv:1007.4839].

[3]M.L.Graesser,I.M.Shoemaker,and L.Vecchi,J.High Energy Phys.1110(2011)110,[arxiv:1103.2771[hepph]].

[4]H.Iminniyaz,M.Drees,and X.Chen,J.Cosmol.Astropart.Phys.1107(2011)003,[arXiv:1104.5548[hepph]].

[5]P.Salati,Phys.Lett.B 571(2003)121,[arXiv:astroph/0207 396].

[6]R.Catena,N.Fornengo,A.Masiero,M.Pietroni,and F.Rosati,Phys.Rev.D 70(2004)063519,[arXiv:astroph/0403614].

[7]E.Abou El Dahab and S.Khalil,J.High Energy Phys.0609(2006)042,[arXiv:hep-ph/0607180].

[8]N.Okada and O.Seto,Phys.Rev.D 70(2004)083531,[arXiv:hep-ph/0407092].

[9]H.Iminniyaz and X.Chen,Astropart.Phys.54(2014)125,[arXiv:1308.0353[hep-ph]].

[10]G.B.Gelmini,J.H.Huh,and T.Rehagen,J.Cosmol.Astropart.Phys.1308(2013)003,arXiv:1304.3679[hep-ph].

[11]S.Z.Wang,H.Iminniyaz,and M.Mamat,Int.J.Mod.Phys.A 31(2016)1650021,[arXiv:1503.06519[hep-ph]].

[12]M.T.Meehan and I.B.Whittingham,J.Cosmol.Astropart.Phys.1406(2014)018,[arXiv:1403.6934[astroph.CO]].

[13]P.Binetruy,C.De ff ayet,and D.Langlois,Nucl.Phys.B 565(2000)169;P.Binetruy,C.De ff ayet,U.Ellwanger,and D.Langlois,Phys.Lett.B 477(2000)285;D.Langlois,Prog.Theor.Phys.Suppl.148(2003)181;E.E.Flanagan,S.H.H.Tye,and I.Wasserman,Phys.Rev.D 62(2000)044039;P.Kanti,I.I.Kogan,K.A.Olive,and M.Pospelov,Phys.Lett.B 468(1999)31;J.M.Cline,C.Grojean,and G.Servant,Phys.Rev.Lett.83(1999)4245;C.Csaki,M.Graesser,C.F.Kolda,and J.Terning,Phys.Lett.B 462(1999)34;C.Csaki,M.Graesser,L.Randall,and J.Terning,Phys.Rev.D 62(2000)045015.

[14]R.J.Scherrer and M.S.Turner,Phys.Rev.D 33(1986)1585,Erratum-ibid.D 34(1986)3263.

[15]P.A.R.Ade,et al.,[Planck Collaboration],arXiv:1502.01589[astro-ph.CO].