A Three Higgs Doublet Model for Fermion Masses∗

Wei Chao(晁伟)

Department of Physics,University of Massachusetts-Amherst,Massachusetts,01003,USA

1 Introduction

In the Standard Model(SM)of particle interactions,charged fermions get masses through the spontaneously broken of the electroweak symmetry and the Higgs mechanism,while neutrinos are massless.AtMZ,the charged lepton masses and the current masses of quarks are given by[1−2]

which show an enormous hierarchy among the Yukawa couplingsyψ.For example,we haveyu/yt∼10−5for the quark sector.

For the neutrino sector,recent results from solar,atmosphere,accelerator and reactor neutrino oscillation experiments show that neutrinos have small but non-zero masses at the sub-eV scale and different lepton flavors are mixed.If neutrinos are Dirac particles,their masses may come from the Higgs mechanism,then we haveyν/yt∼10−12,which seems even unnatural.For the case neutrinos being Majorana particles,the most popular way to explain neutrino masses is the seesaw mechanism.[3−5]If we assume the Yukawa couplings between left-handed lepton doublet and right-handed neutrinos are of order 1,then we havemt/mN∼10−12,which is also unnatural.

In this paper,we attempt to solve or explain the charged fermion and neutrino mass hierarchy problem in the three Higgs doublet model.There are already many excellent literatures focusing on this issue.[6−22]In our model,one Higgs doublet gets its vacuum expectation value(VEV)in the same way as that of the SM Higgs boson,while the other two Higgs fields get their VEVs through the mechanism similar to the way that the scalar triplet gets VEV in the type-II seesaw model‡i.e.,they get their VEVs through their mixings with the SM Higgs.Such that the VEVs can be in the normal hierarchy,which is guaranteed by a spontaneously broken U(1)gauge symmetry.We set them to bev1=100 MeV,v2=10 GeV andv3=173 GeV in our paper.For each generation of charged fermions,there is one Higgs field responsible the origin of their masses.For the neutrino sector,the Higgs doublet that links the Yukawa interactions between the left-handed lepton doublets and right-handed neutrinos is the one that is responsible for the origin of masses of the first generation fermions.Such that the Dirac neutrino mass matrix is naturally small without requiring small Yukawa coupling constants.Then active neutrinos may get small but non-zero masses through a TeV-scale seesaw mechanism.[24]We have to introduce some new fields to cancel anomalies of the U(1)Xgauge symmetry.By applying theZ2discrete flavor symmetry,the lightest neutral component of them can be cold dark matter candidate.We will study its signatures in dark matter direct detection experiments.

The note is organized as follows:In Sec.2 we give a brief introduction to the model,including particle contents,Higgs potential,and scalar mass spectrum.Section 3 is devoted to study the fermion masses.We investigate constraints on the model from electroweak precision measurements and dark matter phenomenology in Secs.4 and 5.The last part is concluding and remarks.

2 The model

We extend the SM with three right-handed neutrinos,two extra Higgs doublet,one Higgs singlet as well as a flavor dependent U(1)Xgauge symmetry.Six generation fermion singletsη(ξ)with U(1)Xhypecharge(−)1 as well as three generation fermion singletsψLwith U(1)Xhypecharge 0 are introduced to cancel the anomalies.The particle contents and their representation under the SU(3)C×SU(2)L×U(1)Y×U(1)Xgauge symmetry are listed in Table 1.We first study how to cancel anomalies of the model.The global SU(2)Lanomaly[29]requires fermions doublet to be even.Considering the conditions for the absence of axial-vector anomaly[30−32]in the presence of U(1)′and the absence of the gravitational-gauge anomaly,[33−35]which requires the sum of U(1)′charge to vanish,one has

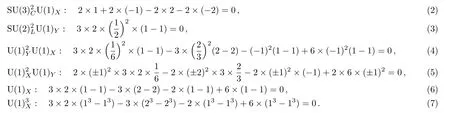
So anomalies are spontaneously cancelled.

Table 1 Particle contents and their quantum numbers under UX(1)gauge symmetry.i=1,2,3 and k=1,...,6.=(uL,dL)T,=(cL,sL)T,=(tL,bL)T,ℓLdenotes left-handed lepton doublets.

Table 1 Particle contents and their quantum numbers under UX(1)gauge symmetry.i=1,2,3 and k=1,...,6.=(uL,dL)T,=(cL,sL)T,=(tL,bL)T,ℓLdenotes left-handed lepton doublets.

U(1)X 1 −1 0 2 −2 0 0 0 0 0 −1 1 0 1 1 1 −1 0 0 1 −1 0 1 SU(2)L 2 2 2 1 1 1 1 1 1 2 1 1 1 1 1 1 1 1 1 2 2 2 1 SU(3)C 3 3 3 3 3 3 3 3 3 1 1 1 1 1 1 1 1 1 1 1 1 1 1 U(1)111222−1−1−1−1 −1 −1 0 0 −1 −1 −1 −1 1−1 110

The most general Higgs potential can be written as

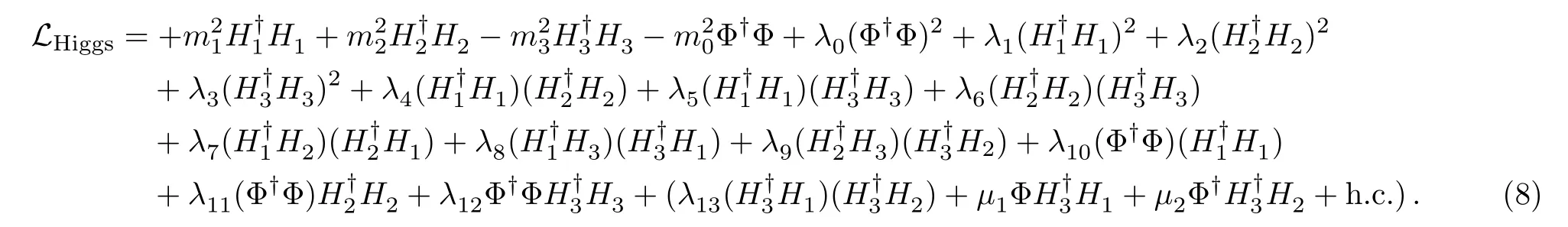
It is obviously thatH1andH2develop no VEVs without terms in the bracket of Eq.(8).The conditions forLHiggsdevelops minimum involve four constraint equations.By assumingandwe have

Let(for simpli fi city)and|µi|≪mi,then we have

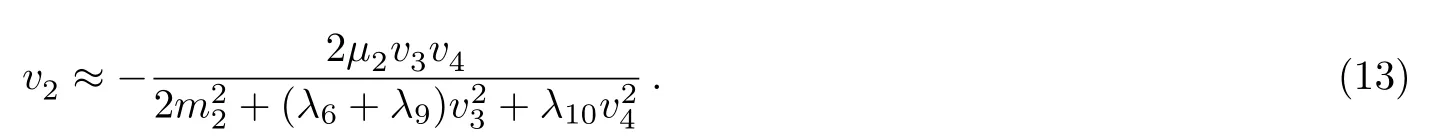
Notice thatv1andv2are suppressed by their masses,which is quite similar to the case that the Higgs triplet get VEV in the type-II seesaw model.So we can get relatively smallv1andv2without con fl icting with any electroweak precision measurements.By settingm1∼10m2andµ1∼µ2we get the normal hierarchal VEVs for the Higgs doublet sector.We setO(v1)∼0.1 GeV,O(v2)∼10 GeV andO(v3)∼100 GeV in our following calculation.In this way the fermion mass hierarchy problem will be fixed,as will be shown in the next section.

After all the symmetries are broken,there are four goldstone particles eaten byW±,ZandZ′.The mass matrix for the CP-even Higgs bosons can be written as

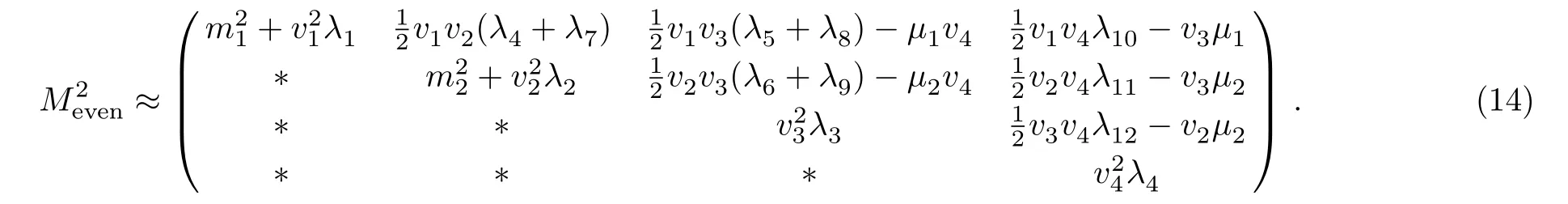
It can be blog diagonalized and the mapping matrix can be written as

whereViis the 2×2 unitary matrix and the expressions ofTandZare listed in the appendix.The corresponding mass eigenvalues are then

wherewith

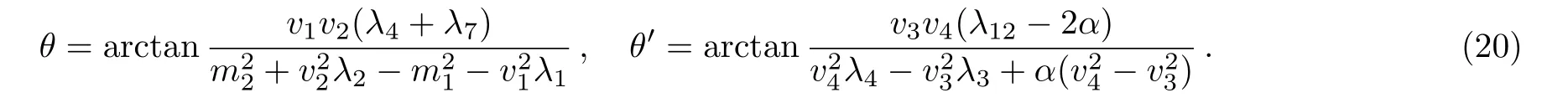
The mass matrix for the CP-odd Higgs fields is

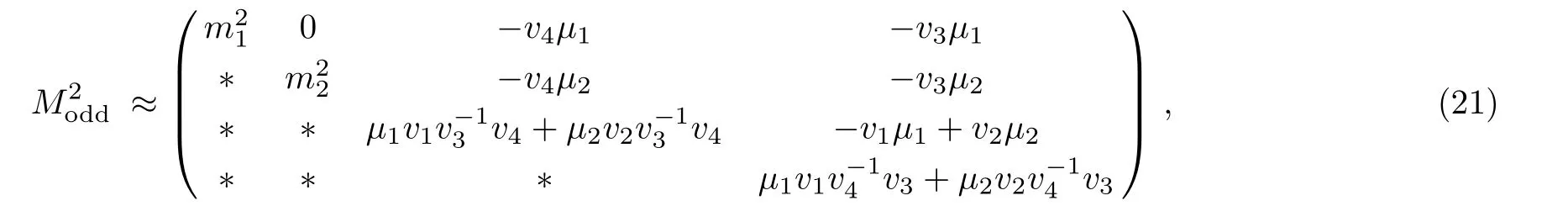
which has two non-zero mass eigenvalues

where

The other two are Goldstone bosons eaten byZandZ′,separately.

Let us give some comments on theZ−Z′mixing.Phenomenological constraints typically require the mixing angle to be less than(1∼2)×10−3[36]and the mass of extra neutral gauge boson to be heavier than 860 GeV.[37]The multi-Higgs contributions toZ−Z′mixing from both tree-level and one-loop level corrections are studied in Ref.[38].A suitable mass hierarchy and mixing betweenZandZ′are maintained by settingv1,v2<10 GeV,v4∼1 TeV andg∼gX.

3 Fermion Masses

Due to the flavor-dependent U(1)Xsymmetry,the Yukawa interaction of our model can be written as

After spontaneous breaking of the U(1)Xand the electroweak symmetry,we get the following mass matrix for the upper-type and down-type quarks:

As we have showed in the last section,viis hierarchal and we setv1=0.1 GeV,v2=10 GeV,andv3=173 GeV in our calculation.For simplification we may also setMuto be nearly diagonal matrices using discrete flavor symmetry,such asZ32.In this case,the mass matrix for the up-type quarks can be written asM′u=diag{Yu11v1,Yu22v2,Yu33v3},whereviis only responsible for the origin of thei-th generation up-type quark masses.Thus all the Yukawa coupling constants,except that of top quark,are ofO(10−2).The down-type quark mass matrix is still what we give in Eq.(24).Even for the most general case of Eq.(24),Yukawa coupling constant can be nearly at the same order.We need to study constraint on the Yukawa couplings from the electroweak precision measurements,which shall be carried out in the next section.

The most general charged lepton mass matrix and Dirac neutrino mass matrix are

The charged lepton mass matrix is quite similar to that in theA4model.[39−40]We set it to be diagonal usingZ2×Z2×Z2flavor symmetry,which is explicitly broken by neutrino Yukawa interactions.In this case the charged lepton mass matrix becomeswhereis of the orderO(10−2)and the Dirac neutrino mass matrix,MD,is the same as that given in Eq.(25).The Dirac neutrino mass matrix is proportional tov1,thusMDcan be at the MeV scale without requiring relatively small neutrino Yukawa couplings.The right-handed neutrino masses may come from integrating out certain high degrees of freedom.For example we may extend our model with three fermion singlet,SL,which transform as(1,1,0,0)under the gauge group SU(3)C×SU(2)L×U(1)Y×U(1)X.It is interaction can be written as

Integrating outSL,we haveIntegrating out heavy right-handed neutrinos,we get the mass matrix of active neutrinos:

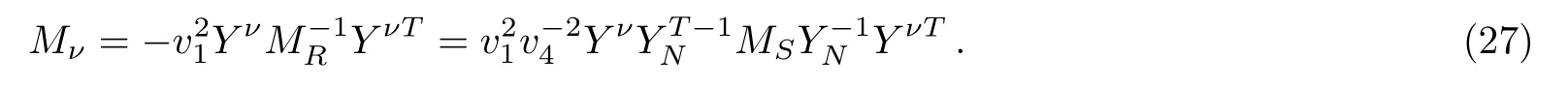
SettingO(Yν)∼10−2,O(YN)∼1 andO(v4)∼MS∼1000 GeV,we derive sub electron-volt scale active neutrino masses.

ηandξget masses after the spontaneous breaking of the U(1)Xsymmetry.Besides they mix with the charged leptons through the Yukawa interactions.To be consistent with the EW precision measurements,we assume the mixing is relatively small.ψLmay get the mass in the same way as that of right-handed neutrinos.It can be stable particle with the help ofZ2flavor symmetry,thus it can be dark matter candidate.It’s phenomenology will be studied in Sec.5.

4 Constraints

There are two major constraints on any extension of the Higgs sector of the SM:theρparameter and the flavor changing neutral currents(FCNC).Notice that in a model with only Higgs doublet,the tree level ofρ=1 is automatically satisfied without adjustment to any parameters in the model.For our model,the constraint fromρis maintained as the constraint on theZ-Z′mixing is fulfilled.However our model does not obey the theorem called Natural Flavor Conservation by Glashow and Weinberg,so that there are tree level FCNC’s mediated by the Higgs boson.In the basis whereMuis diagonalized,MDcan be written as

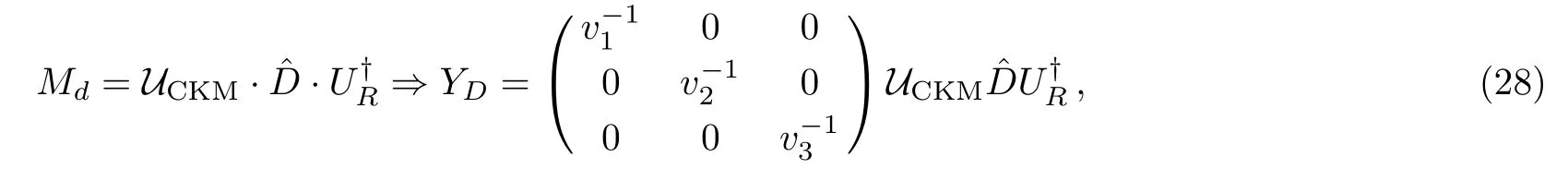
whereis the CKM matrix.The flavor changing neutral current can thus be written as

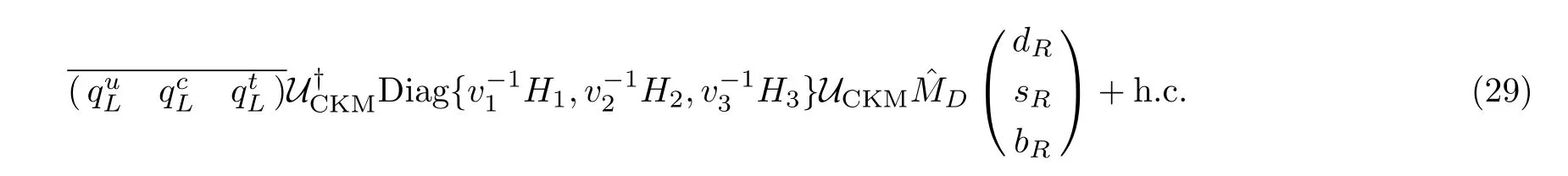
Here we have assumed the mass eigenstates ofHiare nearly equivalent to their flavor eigenstates for simplicity.For the review of various choices of basis in 2HDM,see Ref.[41]for reference.In this section,we consider various processes where FCNC may contribute significantly.Taking into account the experimental values of these processes,we may constrain the parameter spaces of the model.

4.1 K- Mixing

There are two well measured quantities related toK-¯Kmixing:the mass difference and the CP violating observable.Here we only focus on the constraint from the mass difference∆MK,which get its main contribution from the tree level exchange ofh0i.The relevant feynman diagram is given in Fig.1(a).Feynman rules for relevant vertices can be read from Eq.(29):

Thus the mass difference can be derived through the mass insertion method:

Fig.1 Feynman diagrams contributing to various processes.

Fig.2 ∆MK(a)and∆MD(b)as the function of m2the mass eigenvalue of the

UsingfK=114 MeV,mK=497.6 MeV and values of CKM matrix listed in PDG,[1]we plot in Fig.2(a)∆MKas the function ofm2,the mass of the neutral component of the second Higgs doubletH2.In the plot,we have setv1=0.1 GeV,v2=10 GeV,v3=173 GeV as well asm1=20m2,which is natural becausevi(i=1,2)is inverse proportional to theThe horizontal line in the figure is the experimental observed value.To fulfill the experimental constraint,m2should be no smaller than 8.66 TeV in our model.This value might still be accessible at the future LHC.

4.2 D- Mixing

TheD-mixing in our model is a little different from that ofK-¯Kmixing.The contributions to theD-¯Dmixing come from box diagrams,which include the SMW-boson exchange diagram,the two Higgs exchange diagrams,and the mixed exchange diagrams.We assume the two Higgs diagrams dominant the contribution,which is given in Fig.1(b).The following are relevant vertices:

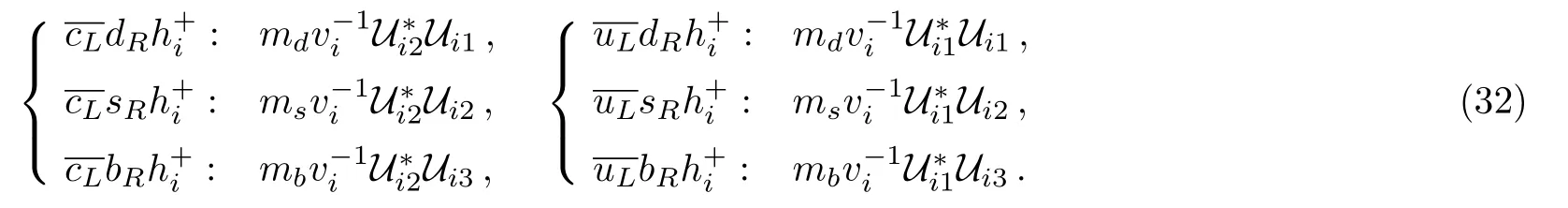
A direct calculation results in

whereyα,yβ=/Λ2and=The explicit expression of integrationI(a,b,c,d)can be found in Ref.[42].

UsingfD=170 MeV andMD=1864 MeV,we plot in Fig.2(b)∆MDas a function ofm2.Our parameter settings are the same as that in theK-mixing study.The horizontal line in the figure represents the experimental value.We can read from the figure that the data ofDmixing constrains the mass ofto be larger than 4.2 TeV.

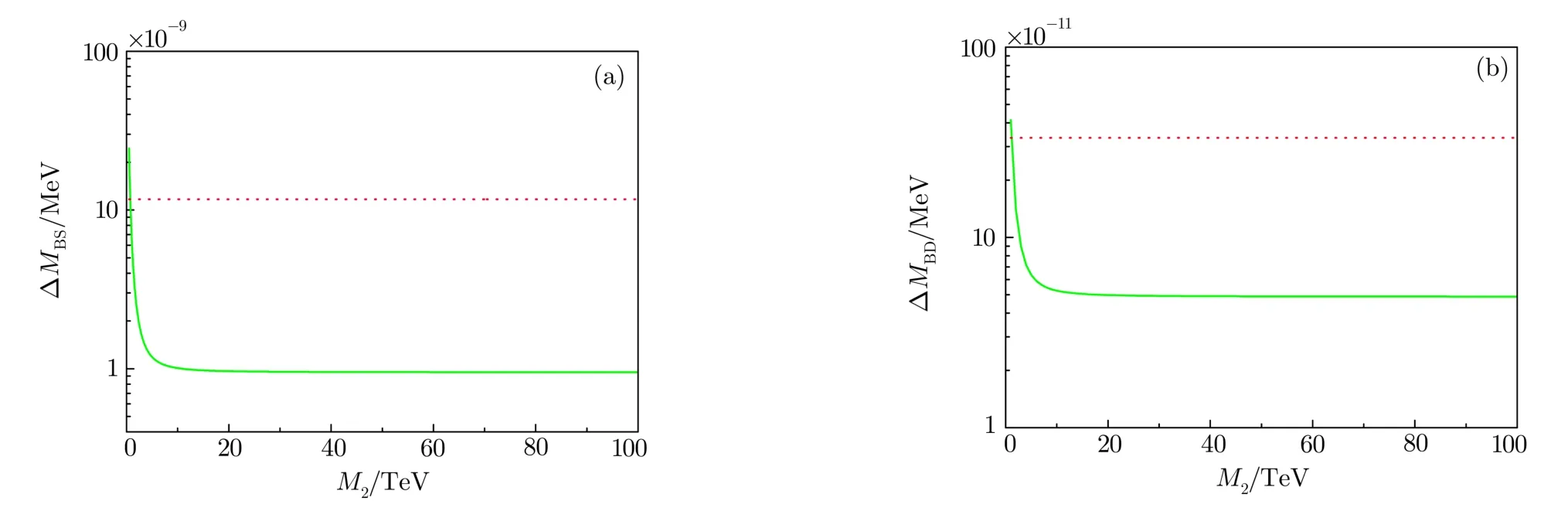
Fig.3 ∆MBS(a)and ∆MBD(b)as the function of m2the mass eigenvalue of the

4.3 B-¯B Mixing

The mass difference in the neutralBmeson system has been well measured by the D0 Collaboration and the CDF Collaboration at the Fermilab Tevatron.Similar to that ofKmixing,there are also tree-level contributions to the∆MBα.The following are relevant vertices that might lead toBα-mixing:

Direct calculation gives

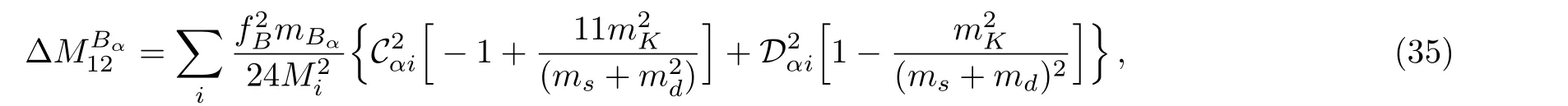
where

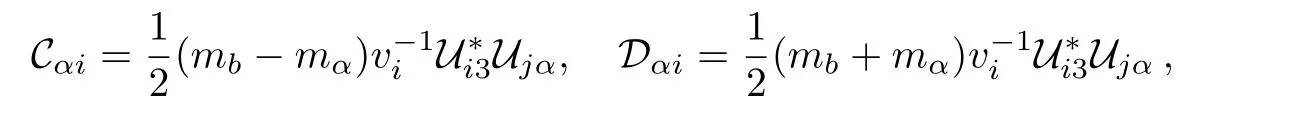
andmBs=5367.5 MeV,mB0=5279.4 MeV.Using the same initial input,we plot in Fig.2(a)∆MB0and in Fig.2(b)∆MBsas the function ofm2,where the horizontal lines in both cases represent the corresponding experimental observed values.Our results show that∆MBαis not so sensitive tom2,which is because the contribution ofH2is heavily suppressed by the CKM matrix.Our numerical results show thatm2should be no smaller than 0.8 TeV.

4.4 µ →eγ

Now we come to the lepton sector and study constraint on the model from lepton flavor violating decays.Among the current available experimental data,µ→eγgives the strongest constraint.We assume the Yukawa matrix for the charged leptons is diagonal,so that the only relevant Yukawa interactions areℓLYν+h.c.Here we only focus on one-loop contributions§§It is claimed in Ref.[43]that the two loop diagrams may be relevant for Higgs bound.to theµ→eγ.The relevant feynman diagram is given in Fig.1(c).Their contribution to theµ→eγcan be written as

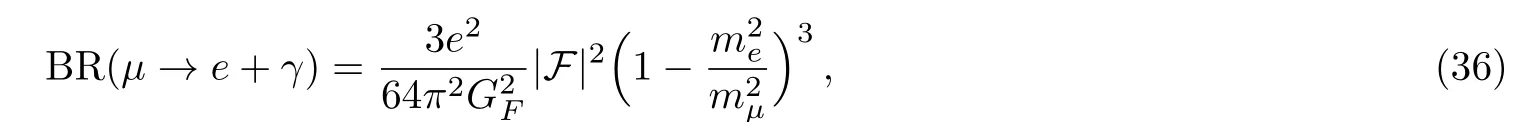
with

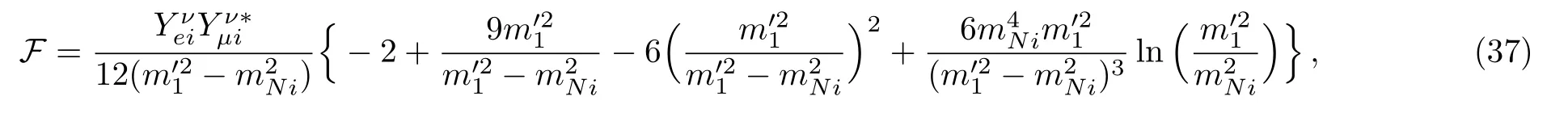
whereis the mass eigenvalue ofandmNiis the mass eigenvalues of right handed neutrinos.In deriving the upper results we have assumedmNi<.

The current experimental upper bounds for the BR(µ→eγ)is 1.2×10−11.[1]By assuming∼4.5 TeV andmNi∼500 GeV,we can get the upper bound for thewhich is of the orderO()∼1,i.e.,there are no severe constraint on the neutrino Yukawa couplings from lepton flavor violating processes.

5 Dark Matter

The lightest neutral fermionψL,which is introduced to cancel the anomalies ofNR,can be stable due to aZ2symmetry and thus can be the cold dark matter candidate.Its relic density can be written as

wherehis the Hubble constant in units of 100 km/s·Mpc,MPl=1.22×1019GeV is the Planck mass,g∗accounts the number of relativistic degrees of freedom at the freeze-out temperature andMZ′is the mass ofZ′with ΓZ′its decay width.We setxfequals to 20 in our calculation,a typical value at the freeze-out for weakly interacting particles.

The elastic scattering cross section of such a dark matter o ffthe nucleon is[44]

We follow the DARKSUSY[45]and use the following inputs for the spin-dependent calculations:

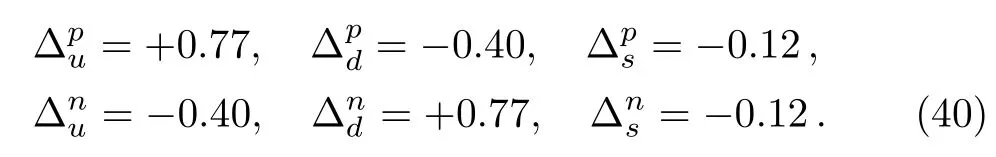
For our model,the coefficientdqcan be written as

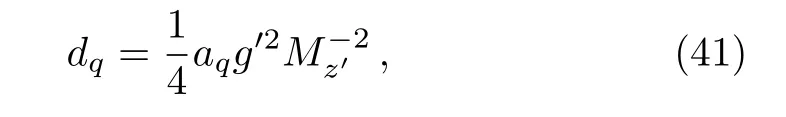
whereaqis the hypercharge of quarks under the new U(1)gauge symmetry.

The cosmological experiments have precisely measured the relic density of the non-baryonic cold dark matter:ΩDh2=0.1123±0.0035.[46]Taking this result into Eq.(38),we may derivegXas the implicit function ofMDMandMZ′.Then one free parameter is reduced.We plot in Fig.4σ(χn→χn)as the function of the mass of the dark matter constrained by the dark matter relic density.The solid and dotted lines correspond toMZ′=600 GeV and 800 GeV,separately.The Xenon-100[47]gives the strongest constraint on the dark matternucleon scattering cross section in the region,which is about[1×10−44,4×10−44].It constrainsMDMlying near 1/2MZ′for our model,around which all the experimental constraints may be fulfilled.

Fig.4 σ(χ+n → χ+n)as function of dark matter mass MDMconstrained dark matter relic density.

6 Conclusion

In this paper,we proposed a possible solution to the fermion mass hierarchy problem by fitting the type-II seesaw mechanism into the Higgs doublet sector.We extended the Standard Model with two extra Higgs doublets as well as a spontaneously broken UX(1)gauge symmetry.The VEVs of Higgs doublets are in normal hierarchy due to the U(1)Xsymmetry.In our model,all the Yukawa couplings of quarks and leptons except that of top quark,are of the orderO(10−2).Constraints on the model from meson mixings,lepton flavor violations as well as dark matter direct detection were studied.The masses of new Higgs fields are constrained to be of several TeV,the collider signatures of which are important but beyond the scope of this paper will be shown in somewhere else.

There are some other reference[48−50]also studying three Higgs doublet models.They try to solve the flavor problem by applying the discrete flavor symmetries to the fermion and scalar sector.It is quite appealing and important.However,it should be noted that to get proper VEVs for these scalars,renormalizable terms,that break the flavor symmetry explicitly,or non-renormalizable terms should be added to the Higgs potential.Thus the scalar VEVs looks quite arbitrary in these models.We use the spontaneously broken U(1)Xgauge symmetry to alignment the interactions of the scalar fields and get unique VEVs for these scalars.Almost all fermion masses come from the Yukawa interactions after the spontaneous breaking of symmetries.It is very appealing since the Higgs mechanism,that is responsible for the EW symmetry breaking and the origin of fermion masses,is quit approaching to be approved.

Aappendix A:Diagonalization of4×4Higgs Mass Matrix

The CP-even Higgs matrix can only be blog diagonalized.We first write it as

whereZ,TandZ′are 2×2 sub-matrix with

[1]K.Nakamura,et al.,(Particle Data Group),J.Phys.G 37(2010)075021.

[2]Z.Z.Xing,H.Zhang,and S.Zhou,Phys.Rev.D 77(2008)113016,[arXiv:0712.1419[hep-ph]].

[3]P.Minkowski,Phys.Lett.B 67(1977)421;T.Yanagida,inWorkshop on unified Theories,KEK report 79-18(1979)95;M.Gell-Mann,P.Ramond,and R.Slansky,inSupergravity,North Holland,Amsterdam(1979)eds.P.van Nieuwenhuizen,D.Freedman,p.315;S.L.Glashow,in1979 Cargese Summer Institute on Quarks and Leptons,Plenum Press,New York(1980)eds.M.Levy,J.L.Basdevant,D.Speiser,J.Weyers,R.Gastmans,and M.Jacobs,p.687;R.Barbieri,D.V.Nanopoulos,G.Morchio,and F.Strocchi,Phys.Lett.B 90(1980)91;R.N.Mohapatra and G.Senjanovic,Phys.Rev.Lett.44(1980)912;G.Lazarides,Q.Sha fi,and C.Wetterich,Nucl.Phys.B 181(1981)287.

[4]W.Konetschny and W.Kummer,Phys.Lett.B 70(1977)433;T.P.Cheng and L.F.Li,Phys.Rev.D 22(1980)2860;G.Lazarides,Q.Sha fiand C.Wetterich,Nucl.Phys.B 181(1981)287;J.Schechter and J.W.F.Valle,Phys.Rev.D 22(1980)2227;R.N.Mohapatra and G.Senjanovic,Phys.Rev.D 23(1981)165.

[5]R.Foot,H.Lew,X.G.He,and G.C.Joshi,Z.Phys.C 44(1989)441.

[6]C.D.Froggatt and Nielsen,Nucl.Phys.B 147(1979)277.

[7]K.R.Dienes,E.Dudas,and T.Gherghetta,Phys.Lett.B 436(1998)55.

[8]I.Gogoladze,C.A.Lee,T.Li,and Q.Sha fi,Phys.Rev.D 78(2008)015024.

[9]H.Frtzsch and Z.Z.Xing,Prog.Par.Nucl.Phys.45(2000)1.

[10]Y.Buchmuller and T.Yanagida,Phys.Lett.B 445(1999)399.

[11]Y.Nir,Phys.Lett.B 354(1995)107.

[12]J.J.Heckman and C.Vefa,Nucl.Phys.B 837(2010)137.

[13]F.Bazzocchi,M.Frigerio,and S.Morisi,Phys.Rev.D 78(2008)116018.

[14]K.Koshioka,Mod.Phys.Lett.A 15(2000)29.

[15]S.Davidson,G.Isidori,and S.Uhlig,Phys.Lett.B 63(2008)73.

[16]G.J.Ding,Phys.Rev.D 78(2008)036011.

[17]C.D.Froggatt,G.Lowe,and H.B.Nielsen,Nucl.Phys.B 414(1994)579.

[18]F.Feruglio and Y.Lin,Nucl.Phys.B 800(2008)77.

[19]A. Aranda, J.L. Diaz-Cruz, and A. Rosado,arXiv:1107.0227[hep-ph].

[20]A.E.Blechman,A.A.Petrov,and G.Yeghiyan,J.High Energy Phys.1011(2010)075,[arXiv:1009.1612[hepph]].

[21]S.Morisi,E.Peinado,Y.Shimizu,and J.W.F.Valle,Phys.Rev.D 84(2011)036003,[arXiv:1104.1633[hepph]].

[22]W.Grimus,L.Lavoura,and B.Radovcic,Phys.Lett.B 674(2009)117,[arXiv:0902.2325[hep-ph]].

[23]R.A.Porto and A.Zee,Phys.Lett.B 666(2008)491;Phys.Rev.D 79(2009)013003.

[24]E.Ma,Phys.Rev.Lett.86(2001)2502;Phys.Lett.B 516(2001)165.

[25]S.M.Davidson and H.E.Logan,Phys.Rev.D 80(2009)095008;T.Morozumi,H.Takata,and K.Tamai,arXiv:1009.1026[hep-ph].

[26]F.Josse-Michaux and E.Molinaro,arXiv:1109.0482[hepph].

[27]N.Haba and O.Seto,arXiv:1106.5353[hrp-ph];Prog.Theor.Phys.125(2011)1155;N.Haba and K.Tsumura,J.High Energy Phys.1106(2011)068;N.Haba and M.Hirotsu,Eur.Phys.J.C 69(2010)481.

[28]W.Grimus and L.Lavoura,Phys.Lett.B 687(2010)188.

[29]E.Witten,Phys.Lett.B 177(1982)324.

[30]S.L.Adler,Phys.Rev.177(1969)2426.

[31]J.S.Bell and R.Jackiw,Nuovo Cimento A 60(1969)47.

[32]W.A.Barden,Phys.Rev.184(1969)1848.

[33]R.Delbourgo and A.Salam,Phys.Lett.B 40(1972)381.[34]T.Eguchi and P.G.O.Freund,Phys.Rev.Lett.37(1976)1251.

[35]L.Alvarez-Gaume and E.Witten,Nucl.Phys.B 234(1984)269.

[36]P.Abreu,et al.,(DELPHI Collaboration),Phys.Lett.B 485(2000)45;R.Barate,et al.,(ALEPH Collaboration),Eur.Phys.J.C 12(2000)183;J.Erler,P.Langacker,S.Munir,and E.R.Pena,arXiv:0906.2345.

[37]J.F.Grivaz,Int.J.Mod.Phys.A 23(2008)3849 and reference therein.

[38]W.Chao and M.J.Ramsey-Musolf,Phys.Rev.D 89(2014)033007,doi:10.1103/PhysRevD.89 033007[arXiv:1212.5709[hep-ph]].

[39]K.S.Babu,E.Ma,and J.W.F.Valle,Phys.Lett.B 552(2003)207.

[40]X.G.He,Y.Y.Keum,and R.R.Volkas,J.High Energy Phys.0604(2006)039.

[41]P.M.Ferreira,H.E.Haber,M.Maniatis,O.Nachtmann,and J.P.Silva,Int.J.Mod.Phys.A 26(2011)769,[arXiv:1010.0935[hep-ph]].

[42]Y.Grossman,Nucl.Phys.B 426(1994)355.

[43]S.Davidson and G.J.Grenier,Phys.Rev.D 81(2010)095016,[arXiv:1001.0434[hep-ph]].

[44]G.Jungman,M.Kamionkowski,and K.Griest,Phys.Rept.267(1996)195,[hep-ph/9506380].

[45]P.Gondolo,J.Edsjo,P.Ullio,L.Bergstrom,M.Schelke,and E.A.Baltz,JCAP 0407(2004)008.

[46]E.Komatsu,et al.,arXiv:1001.4538[astro-ph.CO]

[47]E.Aprile,et al.,XENON 100 Collaboration,Phys.Rev.Lett.107(2011)131302.

[48]A.C.B.Machado,J.C.Montero,and V.Pleitez,Phys.Lett.B 697(2011)318,[arXiv:1011.5855[hep-ph]].

[49]R.Howl and S.F.King,Phys.Lett.B 687(2010)355,[arXiv:0908.2067[hep-ph]].

[50]L.Lavoura and H.Kuhbock,Eur.Phys.J.C 55(2008)303,[arXiv:0711.0670[hep-ph]].