Exact Solutions for a Local Fractional DDE Associated with a Nonlinear Transmission Line

smail Aslan

Department of Mathematics, zmir Institute of Technology,Urla, zmir 35430,Turkey

1 Introduction

Fractional calculus[1−2]has played a very important role in various fields(such as quantum mechanics,elasticity,signal analysis,and many other branches of pure and applied mathematics as well as nonlinear analysis and nonlinear dynamics)because the standard mathematical models of integer-order derivatives,including nonlinear models,do not work adequately in most cases.In fact,fractional calculus[3]begun with the seminal work of Leibniz.It is about a generalization of the ordinary differentiation and integration to non-integer order.In a letter to L’Hospital,Leibniz asked the question: “Can the meaning of derivatives with integer order be generalized to derivatives with non-integer orders?” In recent years,several equations in science and engineering have thus been generalized to non-integer orders so as to provide new models.It can be observed that many applications of fractional calculus amount to replacing the time derivative in a nonlinear evolution equation with a fractional order derivative.Though solving a fractional differential equation(FDE)is a quite difficult task,the theory of FDEs is furnished with some solution methods,theoretical and numerical.Among them are the differential transform method,[4]the Adomian decomposition method,[5]the finite element method,[6]the finite difference method,[7]the homotopy perturbation method,[8]the fractional subequation method,[9]the first integral method,[10]and so on.A good survey on numerical methods for FDEs can be found in Ref.[11].

On the other hand,the significance of differential difference equations(DDEs),or lattice equations,has also been demonstrated in various contexts from engineering to biophysics,chemistry,biology,and some other branches of pure and applied mathematics like nonlinear analysis and nonlinear dynamics.Due to the growing number of applications of DDEs(atomic chains,currents in electrical networks,molecular crystals,chemical reactions,pulses in biological chains,particle vibrations in lattices,and wave phenomena in fluids),some powerful methods are being developed to provide a tool for solving such problems.Among those,the well-known ones are Hirota’s bilinear method,[12]Tau method,[13]Casoratian technique,[14]ADM-Pad´e technique,[15]Exp-function method,[16−21]homotopy perturbation method,[22](G′/G)-expansion method,[23−26]discrete tanh method,[27]etc. Indeed,pioneering ideas of Fermi,Pasta and Ulam[28]have led to many fascinating DDE models such as discrete modified KdV equation,[29]Ablowitz–Ladik lattice equation,[30]Volterra lattice equation,[31]discrete sine-Gordon equation,[32]discrete KdV equation,[33]and Toda lattice equation.[34]Most of the models has the form dun/dt=P(un−1,un,un+1)wherePis a polynomial of its arguments andun(t)=u(n,t),n∈Z,is the displacement of then-th particle from the equilibrium position.

The present study is devoted to a local time-fractional DDE model associated with a previous nonlinear electrical transmission line which reads

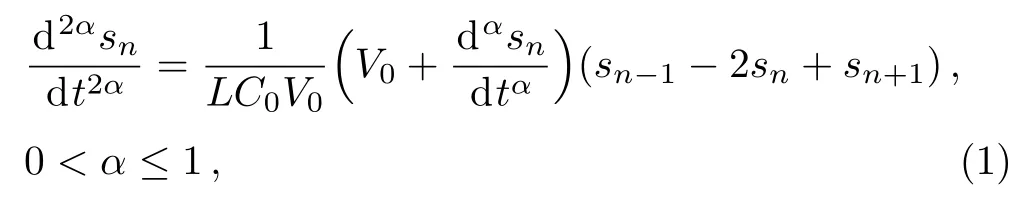
where dαsn/dtαdenotes the local fractional derivative[3]of orderαwith respect tot,sn(t)=s(n,t),n∈Z,Lis a linear inductor,C0andV0are constants.The fractional model(1)is a variant of the classical nonlinear DDE associated with a nonlinear electrical transmission line.[35]In recent years,starting from pioneering ideas going back to Hirota and Suzuki,[36−37]the use of nonlinear transmission lines for studying nonlinear waves and nonlinear modulated waves(pulse solitons,envelope pulse(bright),hole(dark)solitons and kink and anti-kink solitons,intrinsic localized modes(discrete breathers),modulational instability)has drawn much attention by researchers both from the mathematical and physical point of view.Nonlinear electrical transmission lines are discrete systems but approximate the continuum systems quite well.By applying the Kirchho ff’s laws and the continuum approximation to a nonlinear electrical line,Hubertet al.[38]derived an equation of wave propagation and solved it via the Kudryashov method and the(G′/G)-expansion method which provided kink,antikink,and breather soliton solutions.Sardaret al.[39]found multiple traveling wave solutions using three integration schemes(extended tanh method,(G′/G)-expansion method and sine-cosine method)to integrate the model of electrical transmission line. They obtained different kinds of solutions:solitary,shock,singular,periodic,rational and kink-shaped.Malweet al.[40]solved a continuous nonlinear model associated with the previous nonlinear transmission line using the generalized Riccati equation mapping method.Via the Riccati equation mapping scheme,Zhou[41]constructed soliton and soliton-like solutions to the modified Zakharov–Kuznetsov equation in nonlinear transmission line.By applying the variable-coefficient discrete(G′/G)-expansion method,Abdoulkaryet al.[35]investigated exact solutions of the nonlinear DDEs associated with the network.In order to complement the existing literature,in this study,our strategy is to construct exact solutions for the local time-fractional DDE model(1)using the discrete tanh method[27]coupled with the fractional complex transform which was first proposed in 2010 by Li and He[42]to convert FDEs into ODEs.

Here is a brief outlook of the paper.In the next section we focus on the derivatives from a fractional order point of view.In Sec.3 we introduce the fractional complex transform by giving a special example of a local fractional differential equation.Section 4 describes the solution method.In Sec.5 we present our main results.Finally in Sec.6,some concluding remarks are given.

2 Local Fractional Derivative

Some functions(such as Weierstrass’functions)are continuous everywhere,but nowhere differentiable.So,one cannot write down differential equations(to represent some physical dynamical system)to which they can be solutions.To overcome this difficulty,fractional calculus offers several different approaches and definitions for derivatives and integrals of arbitrary order[43]such as the Riemann–Liouville,the Grünwald–Letnikov,and the Caputo derivatives and the Riesz potential.At this stage,it is very crucial to point out that fractional order derivative definitions have their advantages and disadvantages.For instance,[3]the Caputo fractional derivative is defined as

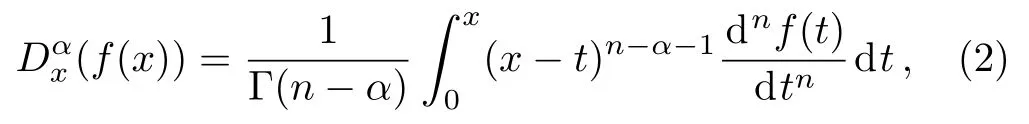
while the Riemann–Liouville fractional derivative is defi ned as

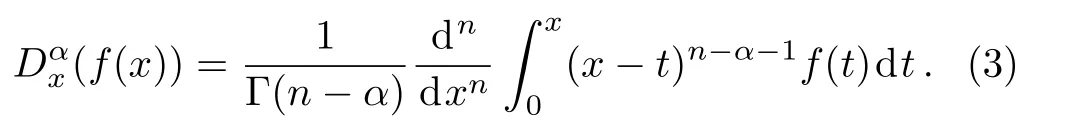
Here dn/dtnstands for the ordinary derivative of integer ordernand Γ denotes the Gamma function.In fact,the Caputo derivatives are defined only for differentiable functions,whilefcan be a continuous(but not necessarily differentiable)function.The Riemann–Liouville definition is suitable for any functions that are continuous but not differentiable anywhere,however,Dαx(f(x)) =0 whenf(x)is a constant.Hence,Jumarie[44]suggested a modification of the Riemann–Liouville fractional derivative,wherefis a continuous(but not necessarily differentiable)function,which reads

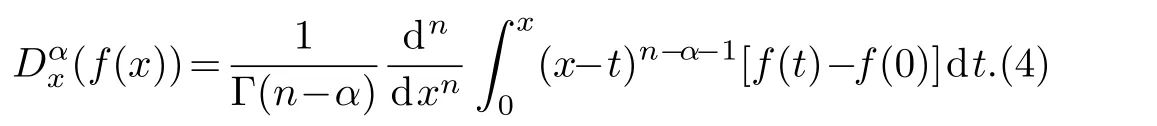
The Jumaire’s fractional derivative(4)has the following properties

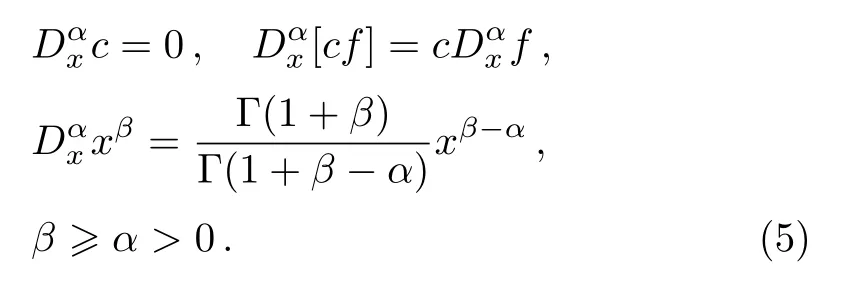
Because of its simple chain rule,recently,the local fractional derivative[3]has attracted much attention,which is defined as

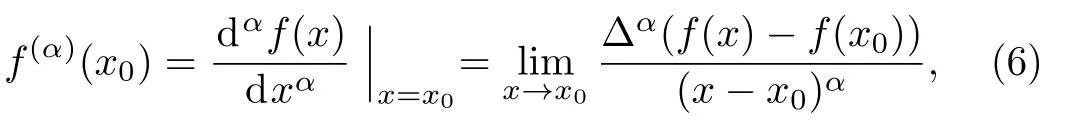
where

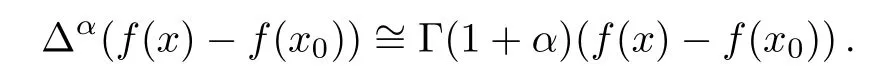
The local fractional derivative(6)obeys the rules

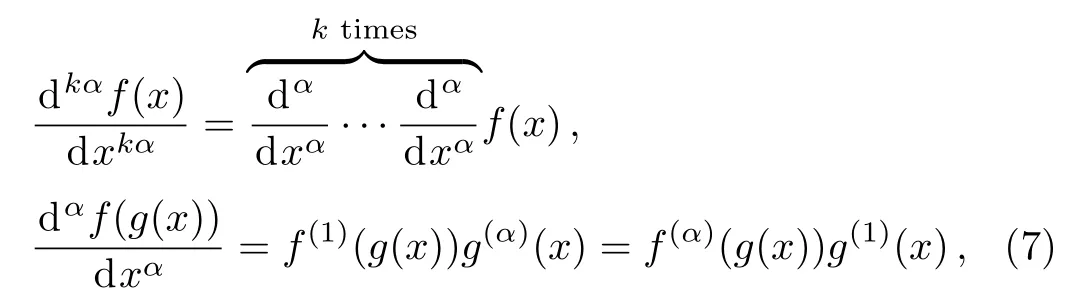
as well as the properties(5)and the product rule

see Ref.[45]for further properties.Similarly,the local fractional partial derivative is defined as

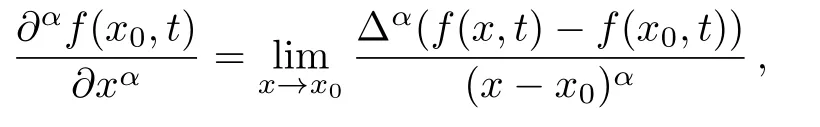
where

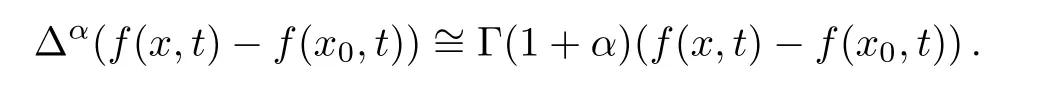
The local fractional derivatives introduced in physical models can describe sound attenuation in complex media.Fractal media,being complex,appears in different fields of physics.

3 Fractional Complex Transform

As is well known,transforms are useful tools in solving problems of applied sciences.To make mention a few;the Laplace transform,the Fourier transform,the wave transformation,the Backlund transformation,the integral transform,etc.The fractional complex transform[3,42]was introduced to convert FDEs in the sense of the Jumaire’s modified Riemann–Liouville derivative to integer order partners. Though many applications of the fractional complex transform appeared in the literature,a counter-example making the approach much skeptical was found.[46]It is observed that the previous demerit can be completely eliminated when the local fractional derivative[3]is used.For example,consider a local fractional partial differential equation[3]in the form

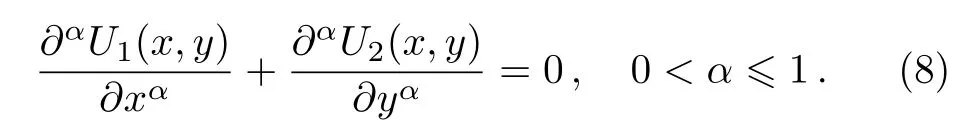
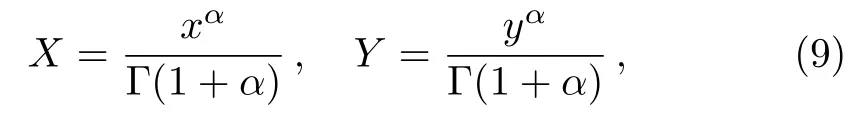
By means of the fractional complex transform one can easily convert Eq.(9)to its differential partner

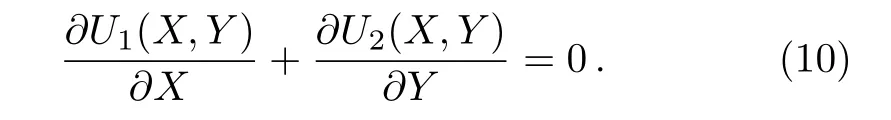
4 Solution Method

The discrete tanh method[27]can be summarized as follows.For a given nonlinear DDE,we construct a system consisting of a differential equation and recurrence relations which read

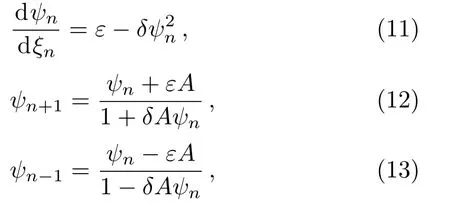
whereξn=kn+λt,andε,δ,A,k,andλare constants.Then,we make the following observations:

(i)Ifε=1,δ=1,A=tanh(k),then the system(11)–(13)has the solutionsψn=tanh(ξn)andψn=coth(ξn).

(ii)Ifε=1,δ=−1,A=tan(k),then the system(11)–(13)has the solutionsψn=tan(ξn)andψn=−cot(ξn).

(iii)Ifε=0,δ=1,A=k,then the system(11)–(13)has the solutionψn=1/ξn.

Now,we consider a system of fractional DDEs in the form

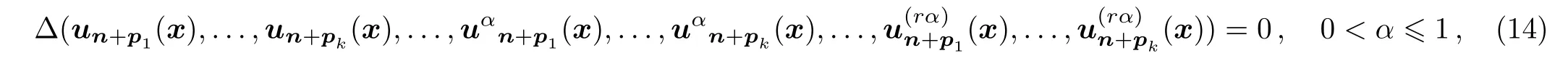
where the dependent variableunhaveMcomponentsui,nand so do its shifts;the continuous variablexhasNcomponentsxi;the discrete variablenhasQcomponentsnj;thekshift vectorspi∈ZQ;andu(rα)(x)denotes the collection of local fractional derivative terms of orderrα.To search for exact solutions of Eq.(14),we first take the fractional complex transformation

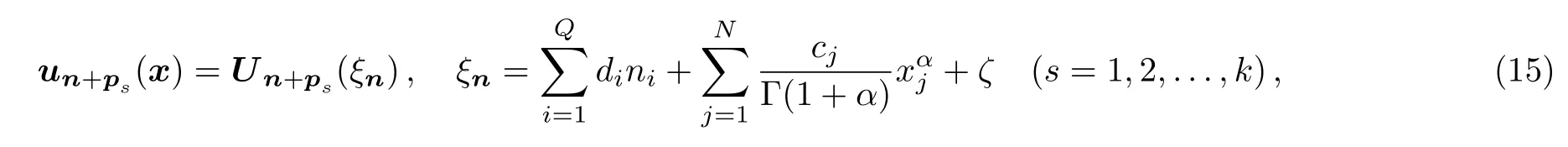
into consideration where the coefficientsc1,c2,...,cN,d1,d2,...,dQand the phaseζare all constants,while the symbol Γ denotes the gamma function.Then,Eq.(14)changes into a system of integer order in the form

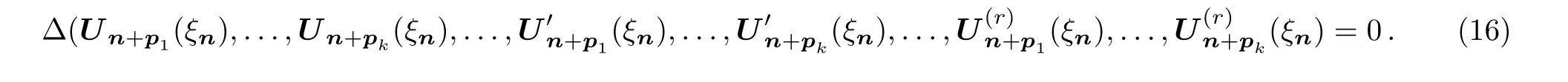
To obtain an exact solution for Eq.(16),a finite expansion

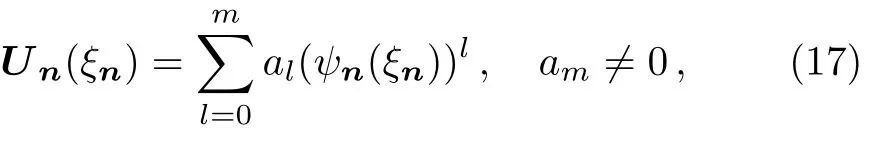
is proposed,wheremis a positive integer,which is usually determined by a homogeneous balance principle,ai’s are constants to be determined,ψn(ξn)is a solution of the system(11)–(13).

5 Exact Solutions for Eq.(1)

Solitary solutions of DDEs have caught much attention because discrete spacetime may be the most radical and logical viewpoint of reality.[47]Indeed,soliton was first discovered in 1834 by Russell,[48]who observed that a canal boat stopping suddenly gave rise to a solitary wave which traveled down the canal for several miles,without breaking up or losing strength.Russell called this phenomenon the “‘soliton”.A soliton is a special traveling wave that after a collision with another soliton eventually emerges unscathed.Today,the study of solitons has been generalized to many areas(such as optics,electrical transmission and various other media)other than water waves.Solitons that occur in electrical transmission lines are commonly refered to as electrical solitons.

In order to integrate Eq.(1),we first introduce the fractional complex transform

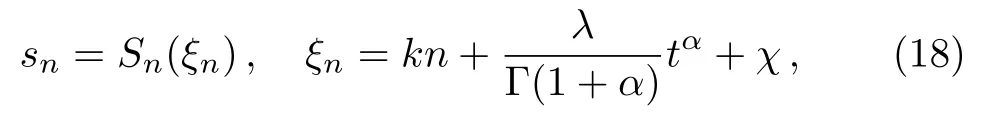
wherekandλare real parameters to be specified,whileχdenotes the phase shift.Substituting Eq.(18)into Eq.(1)gives

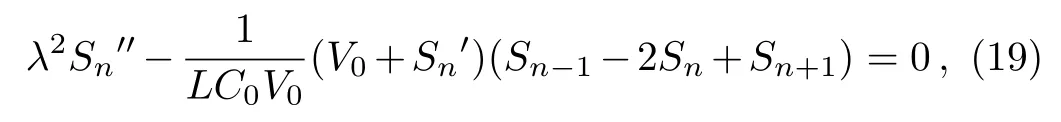
where prime denotes ordinary derivative with respect to the new independent variableξn.Our solution method then suggests looking for exact solutions of Eq.(19)in the form

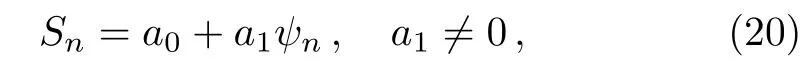
whereψn=ψn(ξn)satisfies the auxiliary equation(11),whilea0anda1are arbitrary constants to be determined at the stage of solving the problem.By means of Eqs.(11)and(20),we get the derivatives

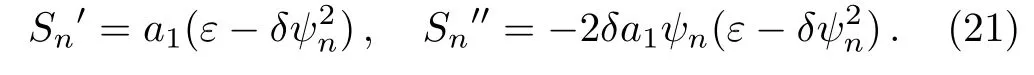
Substituting Eqs.(20)and(21),along with the recurrence relations(12)and(13),into Eq.(19),we obtain a polynomial inψn.Collecting all like termsψin(i=0,1,...)and setting the coefficients to zero yields a nonlinear algebraic system forλ,a0,anda1,which reads

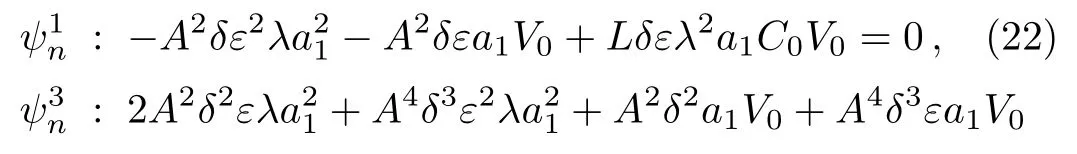
Solving the above system(22)–(25)with the aid ofMathematica,we could get a constrained relation among the parameters as follows

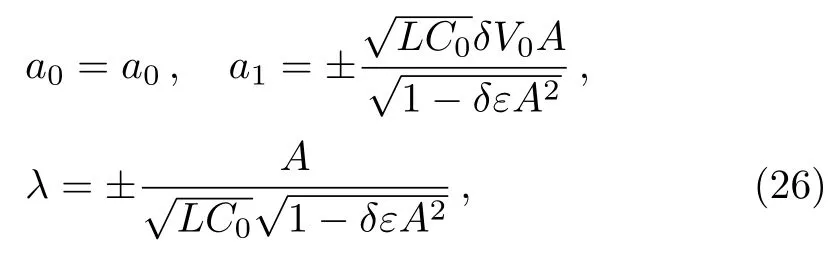
wherea0,δ,ε,andAremain arbitrary.Here and after the signs are ordered in a vertical manner.Then the local time-fractional DDE(1)has the following exact solution

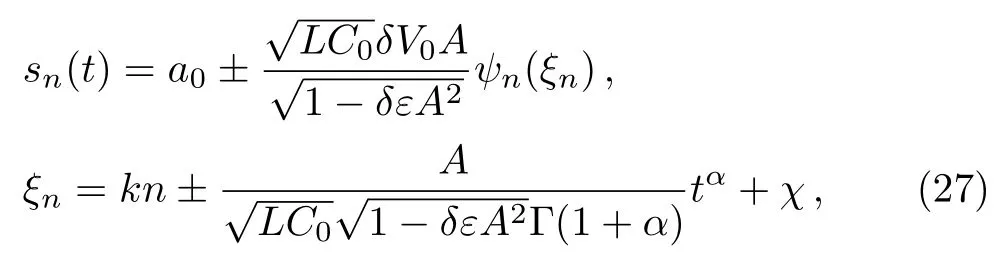
where 0<α6 1,a0,k,andχare arbitrary constants,ψnis the solution of the system(11)–(13).Now,we can construct three types of exact solutions for Eq.(1)as follows:

(i)Whenε=1,δ=1,A=tanh(k),then Eq.(27)leads to the exact solitary wave solutions

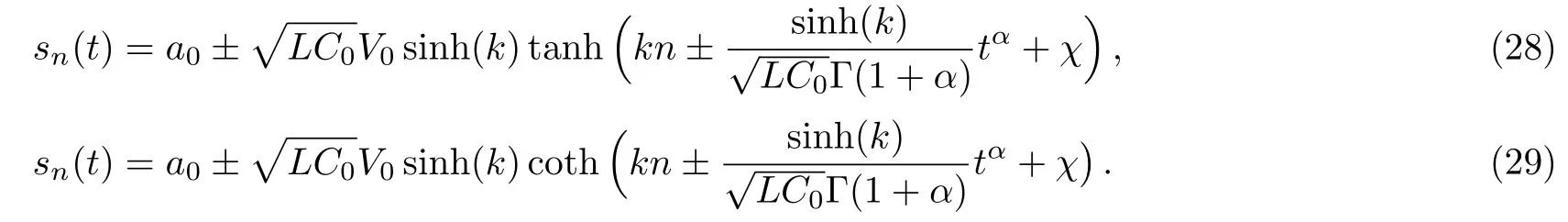
We observe that Eq.(28)is a kink/antikink-type solitary wave solution while Eq.(29)is a singular traveling wave solution(see Figs.1 and 2.).

(ii)Whenε=1,δ=−1,A=tan(k),then(27)gives singular periodic wave solutions

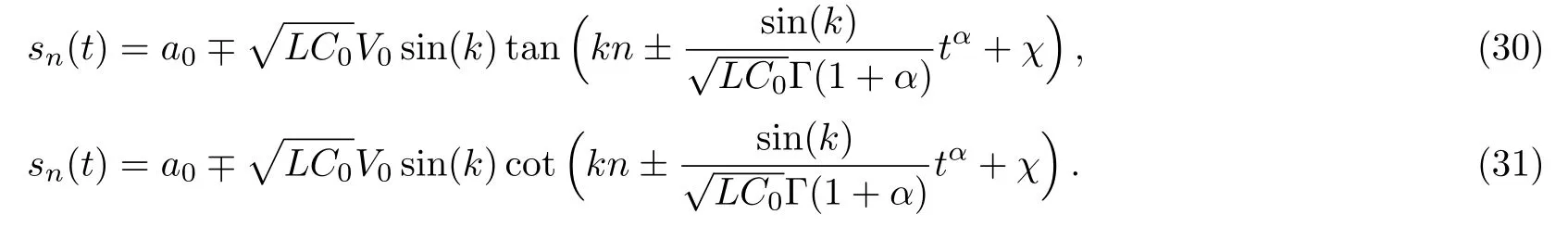
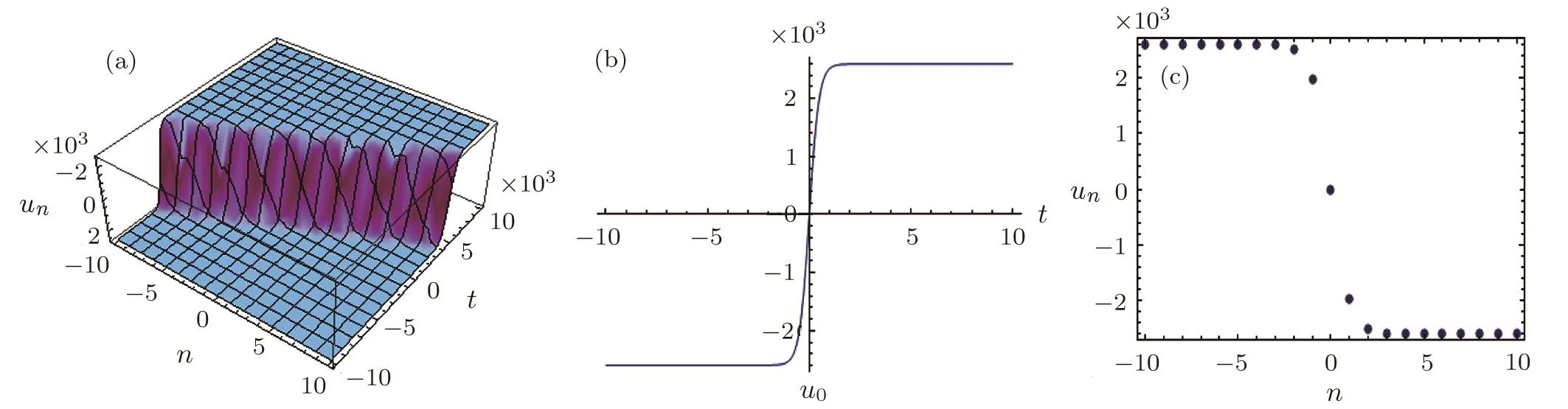
Fig.1 A pro file of the kink-type solitary wave solution(28)with a0=χ=0,k=α=1,V0=3.9 V,C0=470 pF,L=680 µH:(a)−1046 t 6 104,n=0,±1,±2,...,±10;(b)−1046 t 6 104,n=0;(c)t=0,n=0,±1,±2,...,±10.

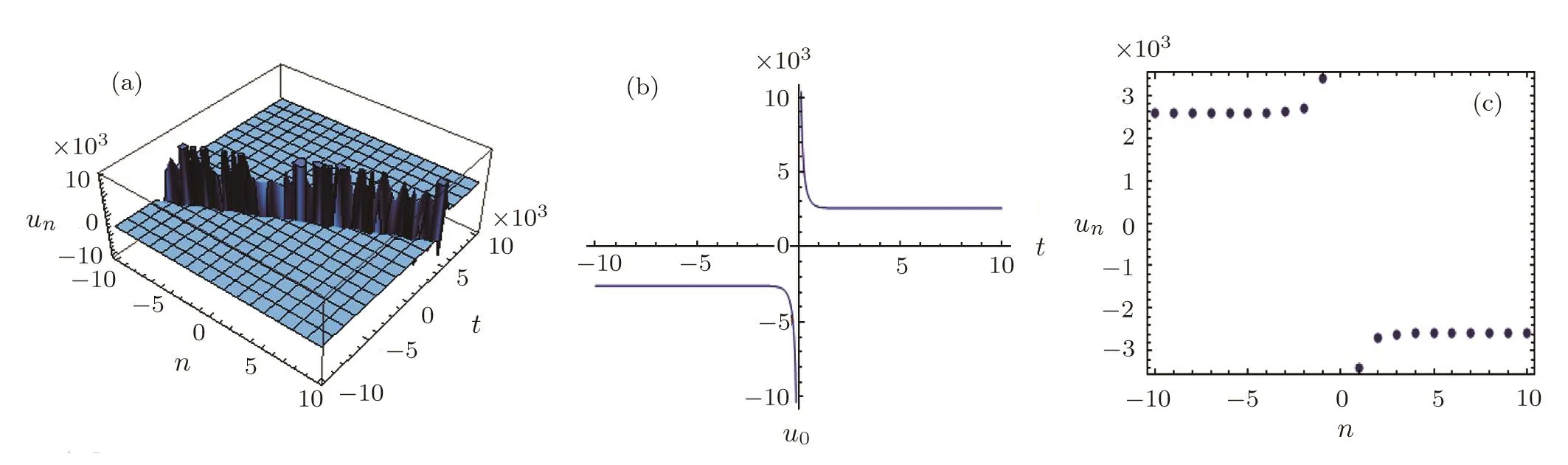
Fig.2 A pro file of the singular traveling wave solution(29)with a0=χ=0,k=α=1,V0=3.9 V,C0=470 pF,L=680 µH,(a)−1046 t 6 104,n=0,±1,±2,...,±10;(b)−1046 t 6 104,n=0;(c)t=0,n=0,±1,±2,...,±10.

(iii)Whenε=0,δ=1,A=k,then Eq.(27)provides a rational solution in the form

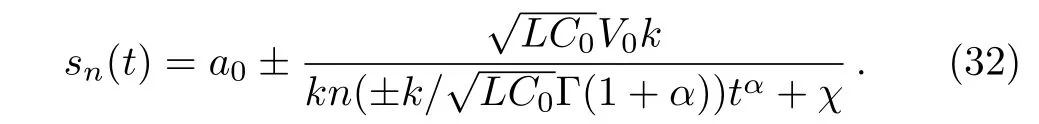
6 Conclusions

From a dynamical view point,the literature exhibits a growing interest in the generalizations of fractional calculus to DDEs.The model which has been considered in this article is a fractional variant of a previous nonlinear DDE associated with a nonlinear electrical transmission line.Local fractional derivative is used due to its simple chain rule.Complexity of fractional calculus,caused partially by non-local properties of fractional derivatives,makes it quite difficult to develop efficient analytic methods.However,it is observed that the discrete tanh method coupled with the fractional complex transform can be used for nonlinear DDEs with localized fractional derivative.Fractional complex transform,which is valid only for general“wave” solutions for FDEs,makes the solution procedure extremely practical.We obtained three types of exact solutions for our model;hyperbolic,trigonometric and rational including antikink/kink-type solitary waves and singular periodic solutions.The local fractional calculus theory is very important for modelling problems on Cantorian space in fractal media.The local fractional derivatives are also useful for solving non-differentiable problems in fractal time-space.We believe that there are still enough freedom degrees in our model for allowing us to analyze it using some other approches.[49]

[1]K.B.Oldham and J.Spanier,The Fractional Calculus,Academic Press,New York(1974).

[2]K.S.Miller and B.Ross,An Introduction to the Fractional Calculus and Fractional differential Equations,Wiley,New York(1993).

[3]J.H.He,Int.J.Theor.Phys.53(2014)3698.

[4]Z.Odibat and S.Momani,Appl.Math.Lett.21(2008)194.

[5]A.M.A.El-Sayed and M.Gaber,Phys.Lett.A 359(2006)175.

[6]Q.Huang,G.Huang,and H.Zhan,Adv.Water Resour.31(2008)1578.

[7]M.Cui,J.Comput.Phys.228(2009)7792.

[8]J.H.He,Int.J.Nonlinear Mech.35(2000)37.

[9]S.Zhang and H.Q.Zhang,Phys.Lett.A 375(2011)1069.

[10]B.Lu,J.Math.Anal.Appl.395(2012)684.

[11]A.A.Kilbas,H.M.Srivastava,and J.J.Trujillo,Theory and Applications of Fractional differential Equations,Elsevier,San Diego(2006).

[12]X.B.Hu and W.X.Ma,Phys.Lett.A 293(2002)161.

[13]A.Saadatmandi and M.Dehghan,Comput.Math.Appl.59(2010)2996.

[14]W.X.Ma and Y.You,Chaos,Soliton&Fractals 22(2004)395.

[15]P.Yang,Y.Chen,and Z.B.Li,Appl.Math.Comput.210(2009)362.

[16]C.Q.Dai and Y.Y.Wang,Phys.Scr.78(2008)015013.

[17]S.Zhang and D.Wang,Therm.Sci.18(2014)1555.

[18]S.Zhang,J.Li,and Y.Zhou,Entropy 17(2015)3182.

[19]S.Zhang,J.Wang,A.X.Peng,and B.Cai,Pramana J.Phys.81(2013)763.

[20]S.Zhang,Q.A.Zong,Q.Gao,and D.Liu,J.Nano Res.23(2013)113.

[21]S.Zhang,Q.Gao,Q.A.Zong,and D.Liu,Therm.Sci.16(2012)1476.

[22]S.D.Zhu,Y.M.Chu,and S.L.Qiu,Comput.Math.Appl.58(2009)2398.

[23]S.Zhang,L.Dong,J.M.Ba,and Y.N.Sun,Phys.Lett.A 373(2009)905.

[24]S.Zhang,Bull.Malays.Math.Sci.Soc.36(2013)699.

[25]S.Zhang,J.M.Ba,Y.N.Sun,and L.Dong,Z.Naturforsch.A 64(2009)691.

[26]S.Zhang,Y.N.Sun,J.M.Ba,and L.Dong,Z.Naturforsch.A 66(2011)33.

[27]Z.Wang,Comput.Phys.Commun.180(2009)1104.

[28]E.Fermi,J.Pasta,and S.Ulam,Collected Papers of Enrico Fermi,Univ.of Chicago Press,Chicago(1965).

[29]R.Hirota,J.Phys.Soc.Jpn.35(1973)289.

[30]M.J.Ablowitz and J.Ladik,J.Math.Phys.16(1975)598.

[31]M.Wadati,Prog.Suppl.Theor.Phys.59(1976)36.

[32]S.J.Orfandis,Phys.Rev.D 18(1978)3828.

[33]Y.Ohta and R.Hirota,J.Phys.Soc.Jpn.60(1991)2095.

[34]M.Toda,Theory of Nonlinear Lattices,Springer-Verlag,New York(1989).

[35]S.Abdoulkary,A.Mohamadou,O.Dafounansou,and S.Y.Doka,Chin.Phys.B 23(2014)120506.

[36]R.Hirota and K.Suzuki,J.Phys.Soc.Jpn.28(1970)1366.

[37]R.Hirota and K.Suzuki,Proc.IEEE.61(1973)1483.

[38]M.B.Hubert,G.Betchewe,S.Y.Doka,and K.T.Crepin,Appl.Math.Comput.239(2014)299.

[39]A.Sardar,S.M.Husnine,S.T.R.Rizvi,M.Younis,and K.Ali,Nonlinear Dyn.82(2015)1317.

[40]B.H.Malwe,G.Betchewe,S.Y.Doka,and T.C.Kofane,Nonlinear Dyn.(2015),doi:10.1007/s11071-015-2318-4.

[41]Q.Zhou,Nonlinear Dyn.(2015),doi:10.1007/s11071-015-2415-4.

[42]Z.B.Li and J.H.He,Math.Comput.Appl.15(2010)970.

[43]E.C.D Oliveira and J.T.Machado,Math.Probl.Eng.2014(2014),Art.ID 238459,6 pp.

[44]G.Jumarie,Comput.Math.Appl.51(2006)1367.

[45]X.J.Yang,Advanced Local Fractional Calculus and its Applications,World Science Publisher,New York(2012).

[46]J.H.He,S.K.Elagan,and Z.B.Li,Phys.Lett.A 376(2012)257.

[47]Y.V.Kartashov,V.A.Vysloukh,A.Malomed Boris,and L.Torner,Rev.Mod.Phys.83(2011)247.

[48]J.S.Russell,York 1844 BA Reports,John Murray,London(1845).

[49]J.Cresson,Fractional Calculus in Analysis,Dynamics and Optimal Control,Nova Science Publishers,New York(2014).