Finite-Time Quasi-Synchronization of Two Nonidentical Chaotic Systems via Intermittent Control∗
2016-05-28YanDong董燕andJinGuoXian咸进国
Yan Dong(董燕) and Jin-Guo Xian(咸进国)
1Department of Mathematics,Shanghai Maritime University,Shanghai 201306,China
2Department of Mathematics,Shanghai Jiao Tong University,Shanghai 200240,China
1 Introduction
During the past decade,chaos synchronization has attracted a lot of interests in various fields,such as mathematics,information technology,applied physics,biology,and social science.This is mainly due to their wide applications in many areas ranging from physics to biological,social and computer sciences.Up to date,many interesting results on synchronization were derived for coupled complex systems.[1−5]However,in reality,especially in some engineering fields,it is desirable and more valuable that the convergence of a dynamical system is realized in finite time rather than in finite time.So,many e ff orts have been made to study finite-time synchronization and many finite-time control techniques have been proposed,including adaptive control,[6−7]impulsive control,[8−9]sliding mode control,[10−11]pinning control,[12]and so on.
In comparison with continuous control of chaos,the discontinuous control method,which includes impulsive control and intermittent control,has attracted more interest recently due to its easy implementation in real physical and engineering systems.Also,it has been shown that,applying controllers to the system continuously would take great costs and seem too impractical in real applications.In this sense,using the discontinuous controllers can lead to the reduction of the control cost.So far,asymptotically synchronization of chaotic systems via discontinuous control was investigated in Refs.[13–17]and so on.In our recent paper,[18]we studied the finite-time synchronization of identically chaotic systems using intermittent control strategy.
In practical situations,parameter mismatch is inevitable in synchronization implementations,and it has significant effects on the collective behaviors of coupled systems.In some cases,parameter mismatches can lead to the loss of synchronization.[19]In other cases,approximate synchronization with a nonzero synchronization error,called quasi-synchronization,can be achieved,[20]which shows the importance of parameter mismatches in synchronization implementations.There have been some reports on synchronization in the presence of parameter mismatches.[21−27]However,most of these studies focus only on the asymptotic quasi-synchronization,but the study of finite-time quasi-synchronization is more valuable.Also, finite-time synchronization has demonstrated better robustness against uncertainties.Therefore,it is of great importance to investigate the finite-time quasisynchronization of nonidentical chaotic systems with parameter mismatches.However,to the best of our knowledge,there have been no studies concerned with this subject.
In thispaper,we study the finite-time quasisynchronization of nonidentical chaotic systems with parameter mismatches via intermittent control.The main contribution of this paper is twofold:(i)the previous studies relating to intermittent control either focused on the finite-time synchronization of identically chaotic systems[18,28]or asymptotical synchronization of coupled nonidentical chaotic systems.[27]Few people put intermittent control,nonidentical chaotic systems and the finitetime synchronization together to study.In this paper,our proposed intermittent control method can ensure the nonidentical chaotic systems with parameter mismatches achieve finite-time quasi-synchronization;(ii)the sufficient conditions for finite-time quasi-synchronization are derived in the form of two simple inequalities,which are easy to check in comparison with those previously reported LMIs.[27−28]Moreover,the explicit expression of error level is given,and the relationships among the error level,parameter mismatches,control period and control width are established.It is shown that the system heterogeneity plays a key role in the error level estimation.Further,the theoretical results contain the finite-time synchronization conditions of chaotic systems with continuous coupling and identical parameters as special cases.In addition,an illustrative example is presented to validate the effectiveness of the theoretical results.
The rest of the paper is organized as follows.Section 2 contains the problem formulation,Sec.3 is the main results.A numerical simulation is presented in Sec.4.The conclusion is given in Sec.5.
Notations:Throughout this paper,∥·∥stands for either the Euclidean vector norm or its induced matrix 2-norm.λmax(A)represents the maximum eigenvalue of the symmetric matrixA.µ(A)=λmax(A+AT).
2 Model and Preliminaries
Consider a general drive-response synchronization scheme with the dynamics of the drive system described by

wherex(t)∈Rndenotes the state vector of the Lur’e system(1);A1∈Rn×n,B1∈Rn×mandC1=(c1ij)n×m=(c11,c12,...,c1m);c1j(j=1,2,...,m)is thej-th column ofC1;the nonlinear functionsatisfies a sector condition withfi(·)belonging to a sector[0,L],i.e.,fi(ξ)(fi(ξ)−Lξ)≤0.
The corresponding response system under consideration is given by
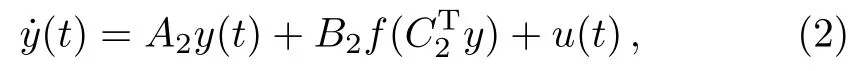
wherey(t)∈Rnis the state vector of the Lur’e system(2);A2∈Rn×n,B2∈Rn×m,andC2=(c2ij)n×m=(c21,c22,...,c2m);c2j(j=1,2,...,m)is thej-th column ofC2;u(t)is the controller.
Definition1Drive system(1)and response system(2)are said to achieve finite-time quasi-synchronization with an error levelϵ>0 if,for any initial statesx(0),y(0),there exists a constantT0>0 such that
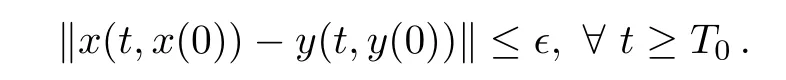
In order to achieve finite-time quasi-synchronization via intermittent control,we design

wheree(t)=y(t)−x(t)is the synchronization error between the drive-response systems(1)and(2),sign(e(t))=diag(sign(e1(t)),...,sign(en(t))),|e(t)|γ=(|e1(t)|γ,...,|en(t)|γ)T,0<γ<1. The coupling strengthsk(t)andη(t)are the intermittent couplings.[13,29]specifically speaking,for the durationnT≤t<(n+θ)T,two systems are switched on andk(t)=k,η(t)=η,wherekandηare positive constants;for the other time(n+θ)T≤t<(n+1)T(n=0,1,2,...),two systems are switched off withk(t)=0,η(t)=0.Here,T>0 is the control period and 0<θ≤1 is called the control width(control duration),whileθ=1,the study is then recovered to the continuous case.
According to Eqs.(1),(2)and(3),the synchronization error between systems(1)and(2)can be written as

wherewith∆A=A2−A1.
To derive our main results,we need the following assumptions and lemmas.
Assumption 1The attractor of the drive system(1)is contained in a bounded set Ω ={x∈Rn|∥x∥≤δ}.
The assumption is reasonable due to the chaotic feature of the Lur’e system.In addition,by Assumption 1,it is clear that the nonlinear functionW(x(t))is bounded,i.e.,

However,the upper bound ofW(x(t))in(5)is rough.For a more precise value,we define

Assumption 2The nonlinearityg(CT2e(t),x(t))belongs to the sector[0,L],i.e.,

Under Assumption 2,the following inequality holds:
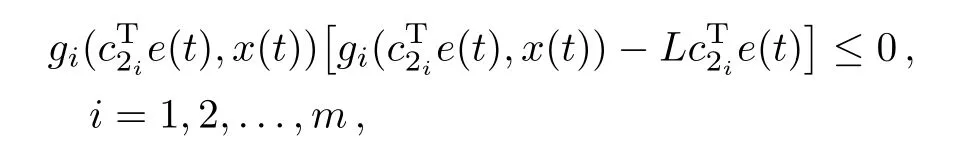
from which we have

where
Lemma 1(Wanget al.[30])Assume that a continuous,positive-de finite functionV(t)satisfies the following differential inequality:

wherec>0,0<η<1 are all constants.Then,for any givent0,V(t)satisfies the following inequality:
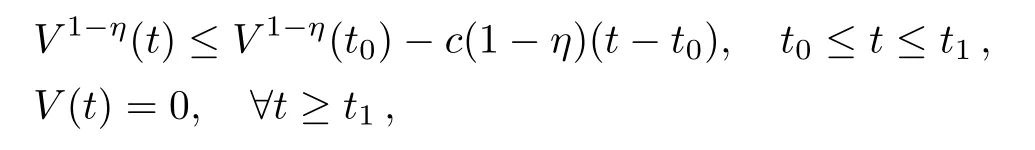
witht1given by

Lemma 2(Jensen’s inequality[31])Leta1,a2,...,an>0 and 0 Lemma 3Suppose thatV(t)is continuous and satisfies ˙V(t)≤g(V),t≥t0.If there exists a time instantT0≥t0such thatV(T0)≤δandg(V)≤0 ifV≥δ,thenV(t)≤δ,∀t≥T0. ProofAssume by contradiction that there exists a time instants>T0such thatV(s)>δ.By the conditionV(T0)≤δ,there exists a time instants1∈[T0,s)such thatV(s1)=δandV(t)>δ,∀t∈(s1,s].Hence,we have(t)≤g(V)≤0,∀t∈[s1,s],which implies thatV(s)≤V(s1)=δ.Note thatV(s)>δ,which leads to a contradiction.The proof is completed. Lemma 4Suppose that a continuous and nonnegative functionV(t),t∈[t0,+∞)satisfies the following conditions: wherek,η,mandϕare positive constants,1/2<γ<1,0<θ≤1.Assume thatk>mand where Π =(ϕ/(k−m)+ϕ/m)(exp{m(T−θT)}−1),then if there exists a time instantT0≥t0such thatV(T0)≤ϕ/(k−m),then ProofSee Appendix. In this section, finite-time quasi-synchronization will be analyzed for the drive-response systems(1)and(2). Theorem 1Suppose that Assumptions 1 and 2 hold.If there exist positive constantsαandβsuch that where then the synchronization error system(4)converges to the setDin finite time,where i.e.,the finite-time quasi-synchronization between systems(1)and(2)is achieved with an error levelProofChoose a Lyapunov function as Taking the derivative ofVwith respect totalong the solution of(4)yields It is clear that Substituting(18)–(20)into(17),we obtain whereMis defined in(14). There are two possibilities forV(t)whent≥0.One is that,for allt≥0,V(t)>βω2/2(k−M);while the other is that there exists a time instantT0such thatV(T0)≤βω2/2(k−M).Case 1 V(t)>βω2/2(k−M),∀t≥0. In the following,we will prove that Case 1 is impossible.In this case,we consider the dynamics ofV(t)for the durationnT≤t<(n+2)T,within which the durationsnT≤t First,the durationnT≤t where we have used the fact thatV(t)>βω2/2(k−M),∀t≥0.Thus,combining(22)and Lemma 1,we have that Second,the durationnT+θT≤t<(n+2)Tis considered.From(21),we have that Thus,from the definition ofk(t),(24)means that:(i)For the durationsnT+θT≤t<(n+1)Tand(n+1)T+θT≤t<(n+2)T, which implies that (ii)For the duration(n+1)T≤t<(n+1)T+θT, which implies that Then,from Eqs.(26),(27),and(29),we have where Ξ>0 is defined in(15).It then follows by condition(12)that IfV((n+2)T)−V(nT+θT)≤0,then based on(23),we have that If 0 where we have used the fact thatV(t)>βω2/2(k−M),∀t≥0.Then,(23)and(33)imply that Combining Eqs.(32)and(34),we have that, whereδ=θTη(1−γ)−(β/2)(1−γ)/2(k−M)(1+γ)/2Ξω1−γ>0 since condition(13)is satisfied.This implies that there must exist a time instantT0such thatV(T0)≤βω2/2(k−M),which contradicts with the fact thatV(t)>βω2/2(k−M),∀t≥0.Therefore,case 1 is impossible. Case 2There exists a time instantT0such thatV(T0)≤βω2/2(k−M). Since Case 1 is impossible,then Case 2 holds.Due to 0<θ≤1,then condition(12)implies thatk>Mand condition(13)implies that further 1/2<(1+γ)/2<1,then the conditions of Lemma 4 are satisfied for system(21),using Lemma 4,we can obtain that Therefore, which means that the finite-time quasi-synchronization between systems(1)and(2)is achieved with an error levelThe proof is completed. Remark 1Theorem 1 provides a reasonably simple finite-time quasi-synchronization criterion,relating to the parameters of system(2),the heterogeneity of the two systems,the control periodT,the control widthθas well as the protocol parametersk,ηandγ.Obviously,for fixed control widthθand appropriately selectedαandβ,condition(12)can be guaranteed by selecting relatively largek.In addition,ifkis determined firstly by(12),thenk>Mdue to 0<θ≤1.Also,0<θ≤1 implies that Ξ>0.Then,for fixed control periodTand appropriately selectedγ,condition(13)can be guaranteed by selecting relatively largeη.In these senses,Theorem 1 implies that,for fixed control periodTand control widthθ,the coupled systems(1)and(2)with intermittent controller(3)can achieve if nite-time quasi-synchronization if the protocol parameterskandηare large enough. Remark 2We emphasize that the parametersk,η,γandθplay important roles in ensuring the finite-time quasi synchronization.specifically speaking,from the proof of case 1 in Theorem 1,we can see that the decrement of the decay of the functionV(t)for the duration[nT,nT+2T)is dominated byδ=θTη(1−γ)−(β/2)(1−γ)/2(k−M)(1+γ)/2Ξω1−γ.That is to say,for fixedk,θ,T,andγ,the convergence rate increases asηincreases.This means that,ηis closely related with the synchronization speed.In addition,by some straightforward arguments,it can be shown that smallerγcan lead to a shorter convergence time if the ratio betweenk−Mand(β/2)ω2is large enough,and largerγcan lead to a shorter convergence time if the ratio betweenk−Mand(β/2)ω2is small enough.Further,from the expression of the error level(16),one can see that the error level decreases askandθincrease. Remark 3Note that,the existing intermittent control methods for studying finite-time synchronization are mostly based on the finite-time stability analysis of the following differential inequality[32] whereV(t)is a continuous and nonnegative function,η>0,0<γ<1,T>0 is the control period,0<θ≤1 is the control width.Further,in order to enrich the results in Ref.[32],Ref.[28]has investigated the finite-time stability of a novel differential inequality,where(t)is smaller thanmV(t)(mis an arbitrary positive constant)when no controllers are added into systems.However,since the above inequalities imply(t)=0 whenV(t)=0,none of them applies to the finite-time quasi-synchronization problem.Here,we have developed Lemma 4 of this paper,where(t)is smaller than a positive constantϕifV(t)turns to be zero.Based on Lemma 4,we have successfully ensured the finite-time quasi-synchronization of nonidentical chaotic systems with parameter mismatches via intermittent control.In addition,our synchronization criterion is very simple,which only involvesMand Ξ to be computed.Thus,it would be easy to check in comparison with those previously reported LMIs. Remark 4It should be noted that,for fixed coupling strengthkand control widthθ,the synchronization error level can be further reduced by the following optimization problem; subject to Eqs.(12)and(13).If the optimization problem has a minimumσ∗,then the drive-response systems(1)and(2)with intermittent controller(3)can achieve finite-time quasi-synchronization with an error levelσ∗ω.Remark 5It should be noted that,if the control process is continuous,i.e.,θ=1,then the error level is recoveredIn addition, finite-time complete synchronization can be achieved if the parameter mismatches vanish.Therefore,the sufficient conditions in Theorem 1 can also be applied to finite-time complete synchronization between two continuous coupled chaotic systems with identical parameters,which shows the generality of the theoretical results derived in this paper. In order to show the effectiveness of the derived results,we consider the following Chua’s circuit as the drive system: with nonlinear characteristic and parametersa=9,b=14.286,c=1,m0=−1/7,m1=2/7 in order to obtain the double scroll attractor(see Refs.[33]and[34].)The Chua’s circuit can be interpreted as the Lur’e systemwhere andf(x)=1/2(|x+c|−|x−c|)belongs to sector[0,1]. The corresponding response system is designed by following the same structure as the drive system but with parameter mismatches in the below Fig.1 Drive-response systems without controller u(t). Fig.2 Evolution of∥W(x(t))∥. By the chaotic feature of the Lur’e system,the drive system and the response system have totally different trajectories due to parameter mismatches.Figure 1 shows the trajectories of the drive system and the response system with initial valuesx1(0)=−0.1,x2(0)=0.2,x3(0)=0.1,y1(0)=0.6,y2(0)=−0.8,y3(0)=−0.6. By simple computation,we obtain that∥B2∥=3.7571,L=1, Figure 2 depicts the evolution of∥W(x(t))∥,from which we getω=2.4688 in(6).Letα=6,β=2,k=23,θ=0.6,T=0.5,η=126,γ=0.01.It follows thatM=9.5768,Ξ=4.1059.Then,the sufficient conditions of Theorem 1 are satisfied and the error level is 5.3995.Thus,we can conclude that the drive-response systems will achieve quasi-synchronization in finite time.Figure 3 gives the simulation result for the error system.Figure 4 compares the derived error level with simulated synchronization error,which shows the conservativeness of the quasi-synchronization conditions. Fig.3 Time evolutions of synchronization error ei(t),i=1,2,3. In Ref.[27],the intermittent linear protocolu(t)=−k(t)e(t)has been proposed to investigate the asymptotically quasi-synchronization of chaotic neural networks with parameter mismatches via intermittent control.To have a fair comparison of the control performance between the finite-time protocol(3)of our paper and the intermittent linear protocol in Ref.[27],we simulate the evolution of the error system according to the intermittent controllers defined in(3)through takingη=150 andη=0.The initial values of the two systems are chosen randomly from the interval[−0.8,0.8].The simulation result is shown in Fig.5.It is easy to see that the finite-time protocol(3)of our paper has a faster convergence speed than the intermittent linear protocol in Ref.[27]. Fig.4 The time evolution of∥e(t)∥ and the estimated error level. The problem of finite-time quasi-synchronization of nonidentical Lur’e systems with parameter mismatches has been discussed,in which an intermittent control scheme has been proposed and the sufficient conditions ensuring finite-time quasi-synchronization have been established based on the Lyapunov stability theory and some differential inequality methods.Moreover,the synchronization error has been explicitly estimated.A simulation result has been presented to demonstrate the effectiveness of our theoretical results.Note that,although we have obtained an explicit expression of error level,the error level estimation is still conservative.This problem needs to be investigated further. Fig.5 The variations of ∥e(t)∥ between systems(1)and(2)with α =6,β =2,k=23,θ =0.6,T=0.5,γ =0.01. Appendix ProofAssume thatT0∈[n∗T,(n∗+1)T)for somen∗>0.Then,eitherT0∈[n∗T,n∗T+θT)orT0∈[n∗T+θT,(n∗+1)T). (i)For the caseT0∈[n∗T,n∗T+θT),according to(8)and Lemma 3,we can conclude thatV(t)≤ϕ/(k−m)for allt∈[T0,n∗T+θT).In addition,(9)implies that Especially,V((n∗+1)T)≤Φ.Whent∈[(n∗+1)T,(n∗+1)T+θT),andV(t)≥Φ, where we have used the conditionsk>mand 0<θ≤1.Then by(42)and Lemma 3,we have Therefore, Next,we will prove that there must exist aT1∈[(n∗+1)T,(n∗+1)T+θT)such thatV(T1)≤ϕ/(k−m).Assume by contradiction thatV(t)>ϕ/(k−m)for allt∈[(n∗+1)T,(n∗+1)T+θT),then(8)implies that Thus,by Lemma 1,we have Further,sinceVis nonnegative and 1/2<γ<1,we can obtain that Then,combining(10)and(47),we can easily obtain that Note thatV((n∗+1)T+θT)≥ϕ/(k−m),which leads to a contradiction.Thus,there must exist aT1∈[(n∗+1)T,(n∗+1)T+θT)such thatV(T1)≤ϕ/(k−m).Then,analyze the dynamics ofV(t)on[T1,(n∗+2)T+θT)similarly to[T0,(n∗+1)T+θT),we can conclude thatV(t)≤Φ,∀t∈[T1,(n∗+2)T+θT)and there exists aT2∈[(n∗+2)T,(n∗+2)T+θT)such thatV(T2)≤ϕ/(k−m).The process repeats,we can fi nally conclude thatV(t)≤Φ,∀t≥T0. (ii)For the caseT0∈[n∗T+θT,(n∗+1)T),the proof is similar to that of case(i),so we omit it.The proof is completed. [1]W.He and J.Cao,IEEE Trans.Neural Networks 21(2010)571. [2]X.Liao and G.Chen,Int.J.Bifur.Chaos 13(2003)207. [3]W.He and J.Cao,Phys.Lett.A 373(2009)2682. [4]J.Lu,J.Cao,and W.C.Ho Daniel,IEEE Trans.Circuits Syst.I 55(2008)1347. [5]W.He and J.Cao,Phys.Lett.A 372(2008)408. [6]M.P.Aghababa,Chin.Phys.B 20(2011)090505. [7]H.Y.Li,Y.A.Hu,and R.Q.Wang,Kybernetika 49(2013)554. [8]J.Mei,M.H.Jiang,W.M.Xu,and B.Wang,Commun.Nonlinear Sci.Numer.Simul.18(2013)2462. [9]W.Xiong and J.J.Huang,Adv.Di ff er Equny 2016(2016)101. [10]S.Li and Y.Tian,Chaos,Solitons&Fractals 15(2003)303. [11]H.Wang,Z.Han,Q.Xie,and W.Zhang,Commun.Nonlinear Sci.Numer.Simul.14(2009)2728. [12]X.H.Liu,X.H.Yu,and H.S.Xi,Neurocomputing 153(2015)148. [13]L.Chen,C.Qiu,H.B.Huang,G.X.Qi,and H.J.Wang,Eur.Phys.J.B 76(2010)625. [14]J.Gao and Z.Y.Wu,Int.J.Mod.Phys.C 22(2011)861. [15]H.J.Shi,Y.Z.Sun,and D.H.Zhao,Phys.Scr.88(2013)045003. [16]G.Wang,Y.Shen,and Q.Yin,Neural Process Lett.42(2015)501. [17]S.M.Cai,P.P.Zhou,and Z.R.Liu,Nonlinear Anal-Hybri 18(2015)134. [18]Y.Dong and J.W.Chen,Int.J.Mod.Phys.C 26(2015)1550095. [19]V.Astakhov,M.Hasler,T.Kapitaniak,A.Shabunin,and V.Anishchenko,Phys.Rev.E 58(1998)5620. [20]G.A.Johnson,D.J.Mar,T.L.Carroll,and L.M.Pecora,Phys.Rev.Lett.80(1998)3956. [21]C.Li,G.Chen,X.Liao,and Z.Fan,Chaos 16(2006)023102. [22]T.Huang,C.Li,and X.Liao,Chaos 17(2007)033121. [23]K.Yuan and J.Cao,In Proc.27th Chinese Control Conf.,(2008)540–543. [24]W.He,F.Qian,J.Cao,and Q.Han,Phys.Lett.A 375(2011)498. [25]W.He,F.Qian,Q.Han,and J.Cao,IEEE Trans.Circuits Syst.I 58(2011)1345. [26]W.He,F.Qian,Q.Han,and J.Cao,IEEE Trans.Neural Netw.23(2012)1551. [27]W.Zhang,J.J.Huang,and P.C.Wei,Appl.Math.Model 35(2011)612. [28]J.Mei,M.H.Jiang,Z.Wu,and X.H.Wang,Nonlinear Dyn.79(2015)295. [29]L.Chen,C.Qiu,and H.B.Huang,Phys.Rev.E 79(2009)045101. [30]H.Wang,Z.Han,Q.Xie,and W.Zhang,Nonlinear Anal.Real 10(2009)2842. [31]G.Hardy,J.Littlewood,and G.Polya,Inequalities,Cambridge University Press,Cambridge(1952). [32]J.Mei,M.H.Jiang,X.H.Wang,et al.,J.Frankl.Inst.351(2014)2691. [33]L.O.Chua,M.Komuro,and T.Matsumoto,IEEE Trans.Circuits Syst.I 33(1986)1072. [34]L.O.Chua,Int.J.Circuit Theory Appl.22(1994)279.



3 Main Results
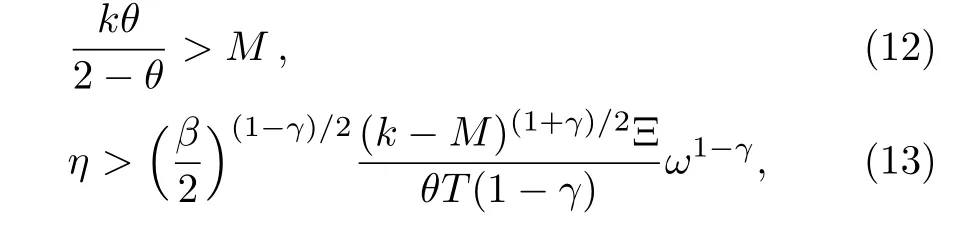















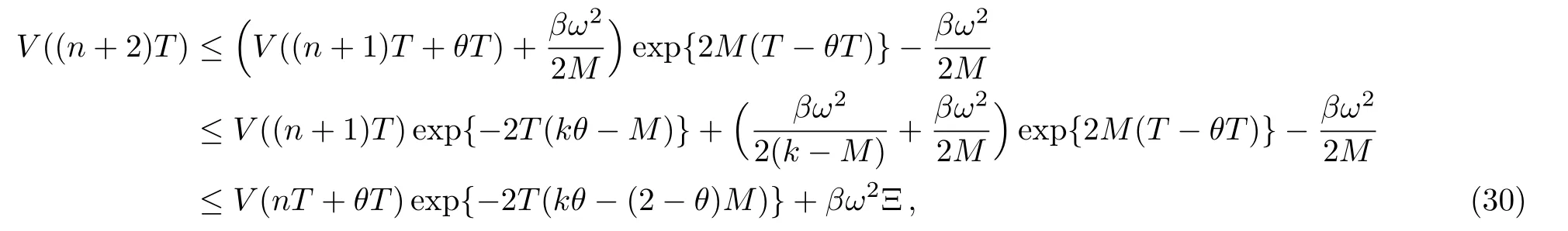
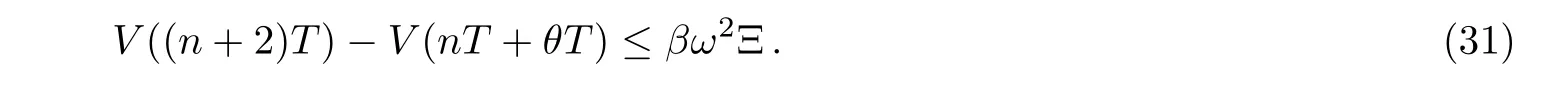

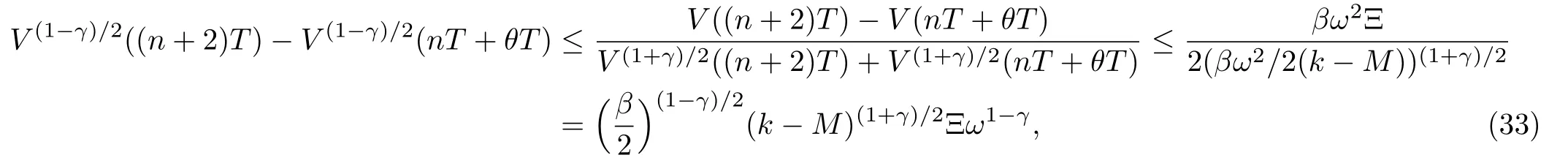





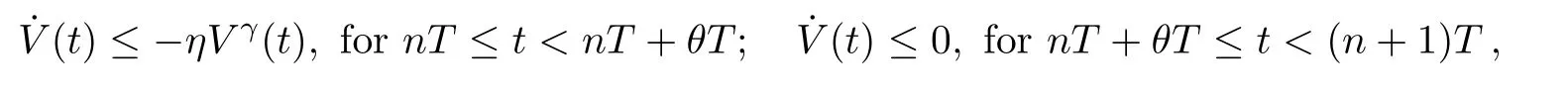
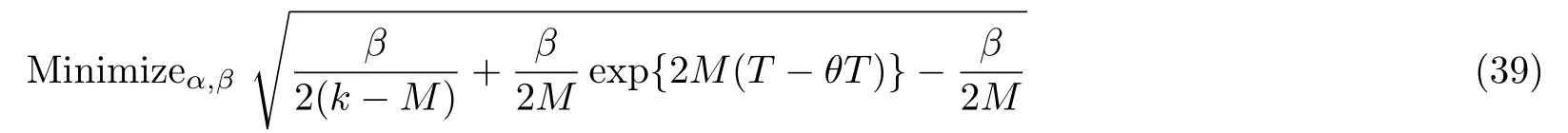
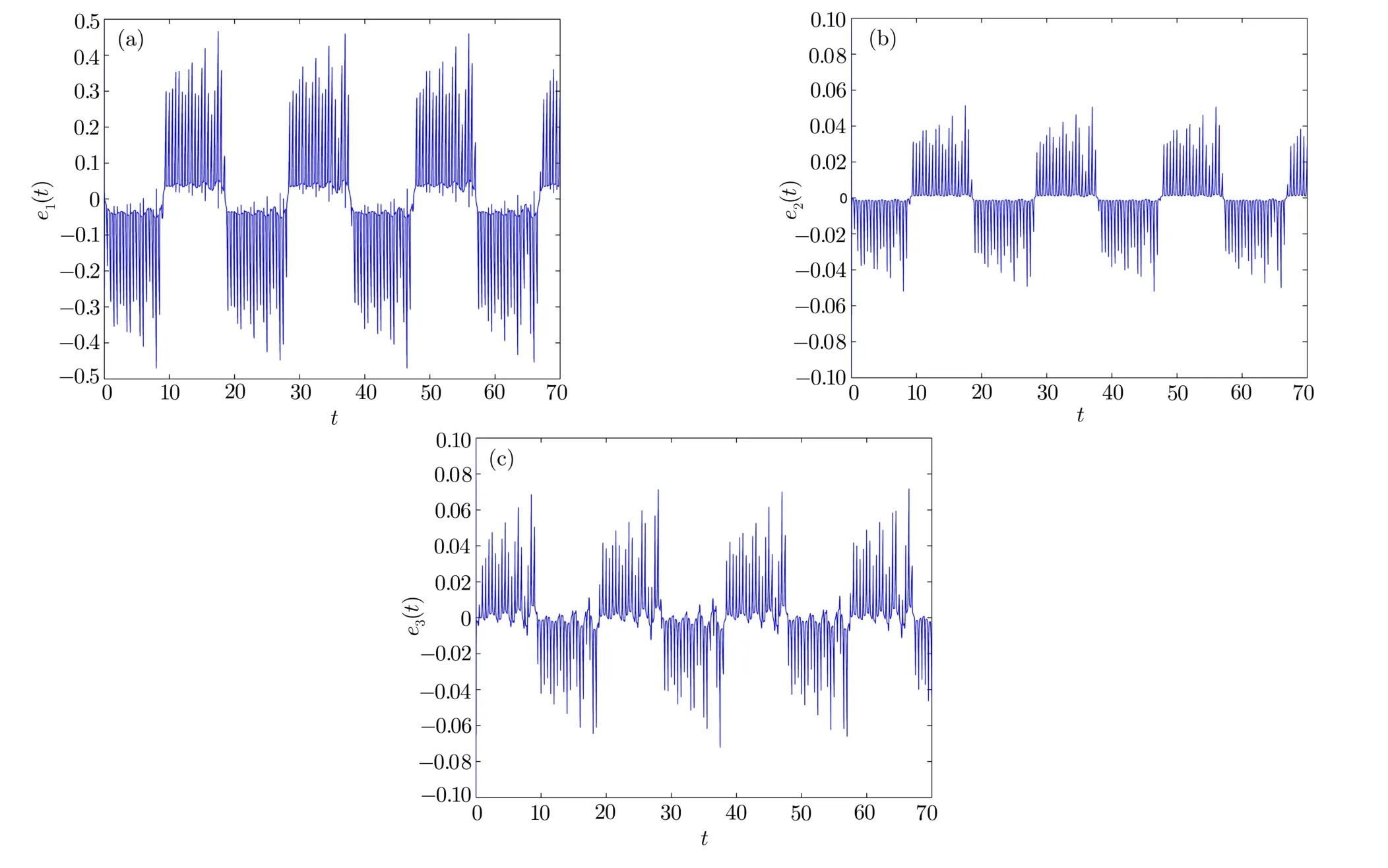
4 Simulation Results

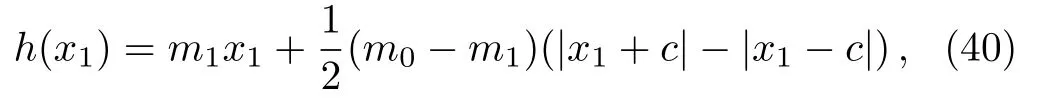






5 Conclusion
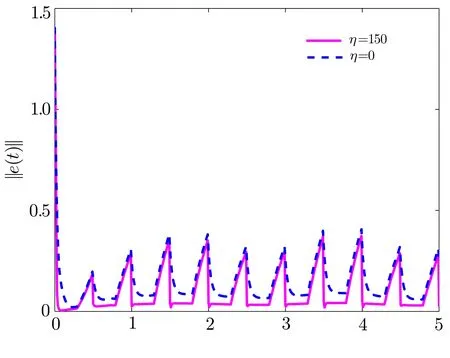

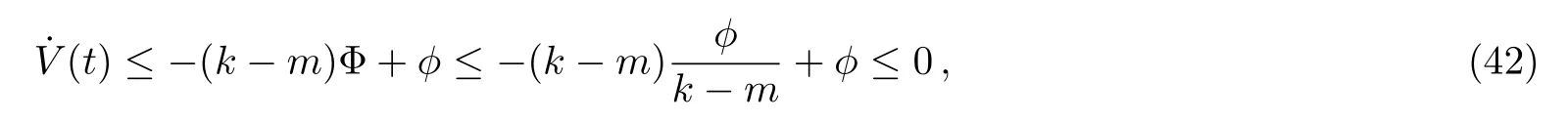






杂志排行
Communications in Theoretical Physics的其它文章
- Self-Focusing/Defocusing of Chirped Gaussian Laser Beam in Collisional Plasma with Linear Absorption∗
- Stationary Probability and First-Passage Time of Biased Random Walk∗
- Analysis of X(5568)as Scalar Tetraquark State in Diquark-Antidiquark Model with QCD Sum Rules∗
- A Three Higgs Doublet Model for Fermion Masses∗
- Lie Symmetry Analysis,Conservation Laws and Exact Power Series Solutions for Time-Fractional Fordy–Gibbons Equation∗
- Critical Behaviors and Finite-Size Scaling of Principal Fluctuation Modes in Complex Systems∗
