Amplitude-Phase Modulation,Topological Horseshoe and Scaling Attractor of a Dynamical System∗

Chun-Lai Li(李春来) Wen Li(李文)Jing Zhang(张敬)Yuan-Xi Xie(谢元喜)and Yi-Bo Zhao(赵益波)

1College of Physics and Electronics,Hunan Institute of Science and Technology,Yueyang 414006,China

2School of Electronic and Information Engineering,Nanjing University of Information Science and Technology,Nanjing 210044,China

3Jiangsu Collaborative Innovation Center on Atmospheric Environment and Equipment Nanjing,Nanjing 210044,China

1 Introduction

Chaos is an interesting yet mysterious phenomenon which can be observed in many natural systems.Chaotic system has been a central issue of renewed interest for researchers since the first discovery in 1963.[1]Many three-dimensional(3D)autonomous chaotic systems with quadratic nonlinearities,such as Chen system,[2]Lü system[3]and some other Lorenz-like systems,[4−14]have been presented by developing Lorenz model.For these chaotic systems,careful but common analyses are carried out,whereas the issue of amplitude and phase modulation,which may be more problematic,has not been studied in depth.

Amplitude and phase modulation of chaotic signal are important in engineering and technological applications.It turns out that the amplitude modulation system can yield the desired signal amplitude without any accessional circuitry,thus it can reduce the hardware spending and decrease the probability of failure in circuit implementation,and can also avoid the influence of the band-limit fi lter in signal ampli fi cation circuit.[15−17]In addition,this kind of system can provide a new security encoding key.[16]Therefore,from a control engineering point of view,it is a promising type system for providing an actual test platform for chaotic communication and advanced control techniques.

Generally,for these amplitude modulation systems with quadratic nonlinearities,the amplitude control parameters are the coefficients of quadratic terms,which can adjust partial or all of the signal amplitude of system variables nonlinearly.[15−17]Actually,the coefficient of the single nonlinear term can modulate the signal amplitude since it uniquely determines the scale of the variables.As an illustration,we consider the chaotic system with a single nonlinear term as˙x1=x2,˙x2=x3,˙x3=bx1−x2−ax3−bx31.[18]With the transformationx1→k−0.5x1,x2→k−0.5x2,x3→k−0.5x3,the system becomes˙x1=x2,˙x2=x3,˙x3=bx1−x2−ax3−(b/k)x31.Therefore,coefficientbof cubic nonlinearityx31can scale the amplitude ofx1,x2,x3according to power function with the index–0.5.However,for these systems with a single linear term such as˙x1=−x2−x2x3,˙x2=x21+14x1x3,˙x3=x2x3+x23,the coefficient ofx2can modulate both amplitude and frequency of the signals because it is the only term of which the dimension is different from the remaining quadratic terms.[19]From what has been discussed above,an interesting yet interrogative question is whether each coefficient of non-single linear terms in chaotic system can modulate the signal amplitude.

As a rigorous theory and a powerful tool for the investigation of chaotic dynamics,topological horseshoe is based on the geometric analysis of continuous maps on some subsets of state space.For any point of the space subsets,we can find its image under Poincar´e map by using short-term computation.Since one just needs to solve the piece of trajectory between the point and its Poincar´e image,the numerical error is much smaller than long-term computation for Lyapunov exponent spectra.So,compared with Lyapunov exponents,we can acquire more information and detailed dynamics of chaotic system from topological horseshoe.The pioneering work for topological horseshoe is the chaos lemma for continuous map proposed by Kennedy.[20]Then,Yang obtained a significant result for topological horseshoe of non-continuous map.[21]Recently,Li presented a new method for seeking horseshoe in continuous chaotic system,[22]which has been applied to verify the existence of chaos for some practical systems.[15,23−26]

On the other hand,the issue of scaling attractors of some typical nonlinear systems was investigated with the help of projective synchronization,which means that the drive signalxdand the response signalxrcan be synchronized up to a nonzero scaling factor.[27−31]Scaling factor describes the dynamics of projective synchronization in partially linear chaotic systems and can expand the mode for encoding data and achieve communication rapidly.[16,32]Besides,the scaling factor in projective synchronization can additionally enhance the security of communication since it is unpredictable.[33−35]

Enlightened by the above analyses,a 3D quadratic chaotic system is considered in this paper. The main peculiarity of this system is that the signal amplitude can be modulated via controlling the coefficients of the linear term,cross-product term and squared term simultaneously or respectively,and that the phase ofx3can be modulated by the coefficient product of the linear term and cross-product term.What is more,the fl exible selection and combination of modulation coefficient will turn out different modulation type.Some basic dynamical properties of the system,such as phase portrait,Poincar´e map,continuous spectrum,Kaplan–Yorke dimension,Lyapunov exponent spectra,and signal amplitude,are studied by theoretical analysis and dynamic simulation.Then,the topological horseshoe of this system is studied by carefully selecting cross-section and Poincar´e map,which gives a rigorous theoretical veri fi cation of the existence of chaotic behavior in this system.Finally,the chaotic attractor of this system is scaled by modified projective synchronization(MPS)with a single linear coupling scheme.Particularly,based on the constructed performance function of the controller,which decides the lowest control consumption,the optional control gain is selected.Because the scaling factors in projective synchronization are determined only by the system parameters and thus can be regarded as the encoding key,the introduced scheme is more useful and safer for real-time encryption and decryption in secure communications than the existed synchronization method.[27−29]

The rest of this paper is organized as follows.In Sec.2,the 3D chaotic system is presented,and some basic dynamical properties are analyzed to verify the existence of chaos.In Sec.3,amplitude and phase modulation property is analyzed in detail.In Sec.4,topological horseshoe of the introduced system is investigated.In Sec.5,we focus on scaling chaotic attractors of the system by MPS.Finally,conclusion is drawn in Sec.6.

2 The 3D Dynamical System

2.1 System Description

The discussed 3D quadratic autonomous system is described as

In system(1),x1,x2,x3are the state variables,anda,b,f,g,hare the constant parameters.System(1)is found to be chaotic witha=10,b=6,f=1,g=1,h=1,as depicted in Fig.1.

2.2 Poincar´e Map,Power Spectrum and Kaplan–Yorke Dimension

The chaotic feature can be further illustrated by Poincar´e map and continuous power spectrum,as shown in Fig.2.It appears from Fig.2 that the proposed attractor displays complicated dynamical behaviors.

The three Lyapunov exponents of system(1)is calculated as(0.86473,4.15×10−4,−8.07802)whena=10,b=6,f=1,g=1,h=1.Therefore,we obtain the corresponding Kaplan–Yorke dimension as

DKY=2+(0.86473+4.15×10−4)/8.07802=2.1071,which is fractional,and system(1)is a real dissipative system.The essence of the fractal does not merely mean the system has non-periodic orbits;it also causes adjacent trajectories to diverge.Similar to all other chaotic attractors,orbits leaving from different initial conditions will soon reach the attracting set.These orbits do not stay close to each other but diverge and follow utterly different trajectories in the attractor.Therefore,system(1)is indeed a new chaotic dynamical system.

2.3 Symmetry

Generally,the symmetry property widely exists in the dynamical systems with an even number of attractors.It is easy to know from Eq.(1)that the proposed system is symmetric with respect to thex3-axis,as shown by the coordinate transformation(x1,x2,x3)→(−x1,−x2,x3).

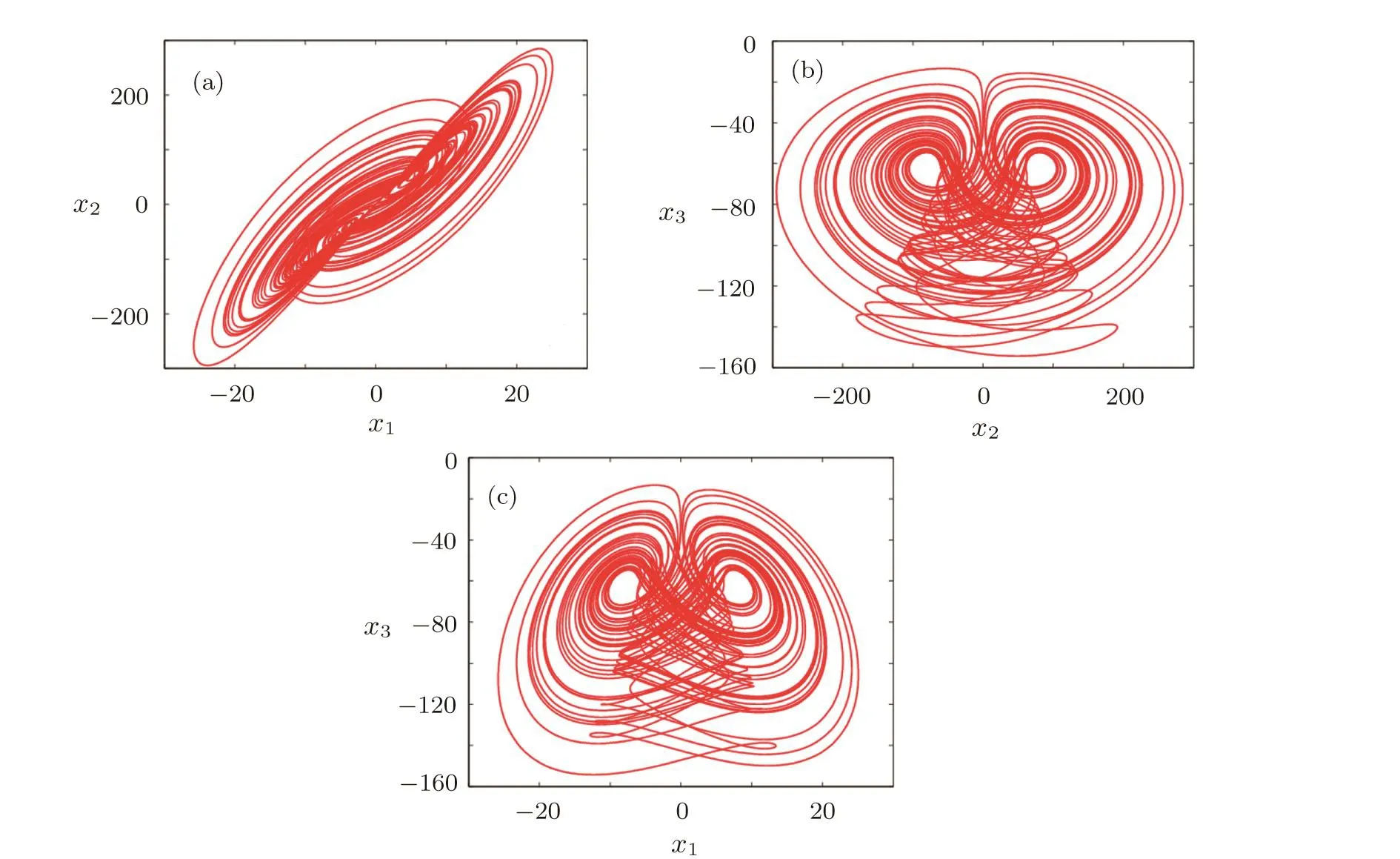
Fig.1 (a)x1-x2phase portrait;(b)x2-x3phase portrait;(c)x1-x3phase portrait.

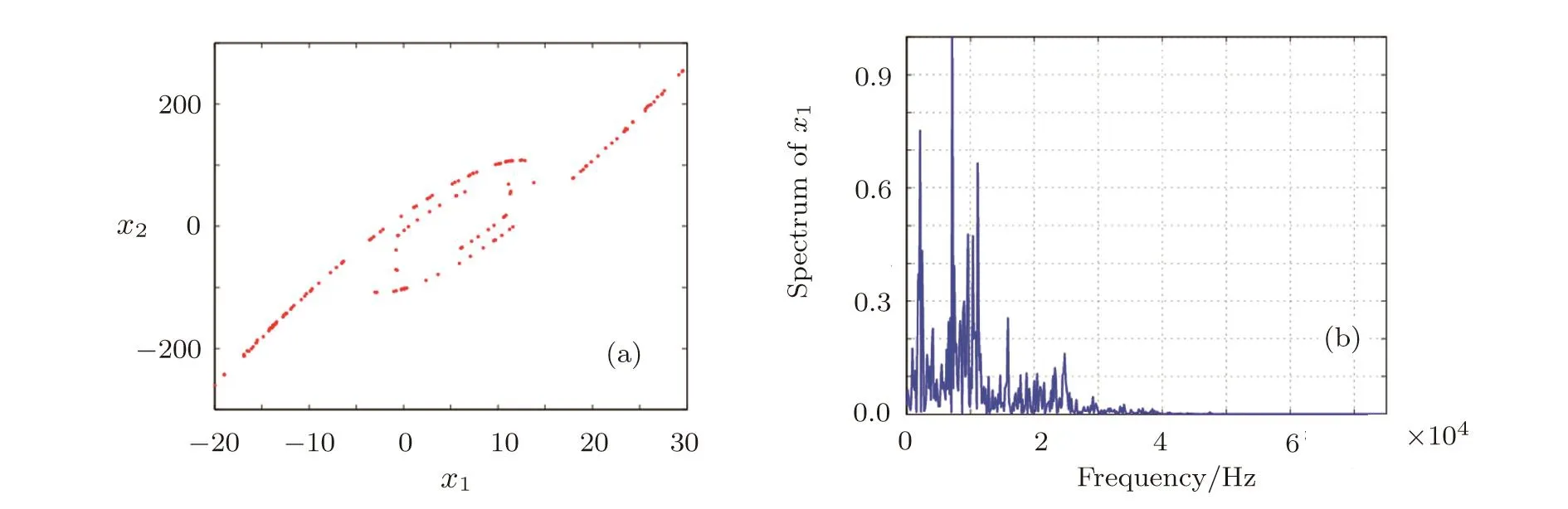
Fig.2 (a)Poincar´e map with x3= −100 and(b)power spectrum of time series x1.

3 Amplitude and Phase Modulation Property of System(1)

The main finding for the proposed system is that the signal amplitude can be modulated via controlling the coefficients of the linear term,cross-product term and squared term simultaneously or respectively,and the phase of signalx3can be modulated by the product termfg,which discriminate from the existent results in Refs.[15–17,19].

Theorem 1The coefficientsf,g,hmodulate the signal amplitude of variablesx1,x2,x3according torespectively.And the Lyapunov exponent spectrum remains constant when these coefficients vary.

Proofv3/(fg),the deduced system of Eq.(1)is expressed as

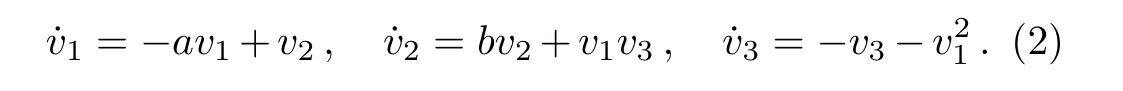
The resulting system(2)is identical to system(1)withf=g=h=1.Therefore,The coefficientsf,g,hmodulate the signal amplitude of variablesx1,x2,x3accordingrespectively.

System(1)possesses three equilibrium points,as below

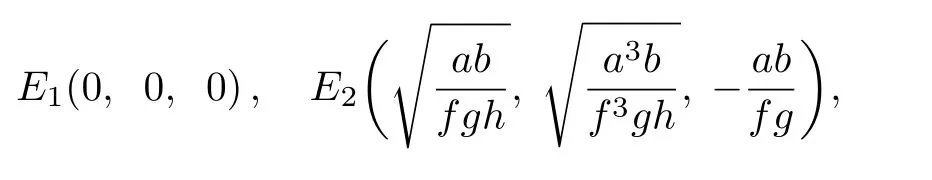
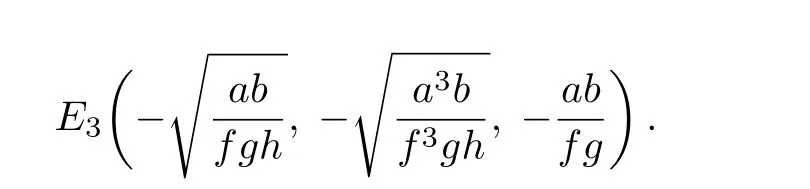
The corresponding characteristic equation of system(1)evaluated at equilibrium point(x1E,x2E,x3E)is depicted by

Considering equilibrium pointE0,we obtain

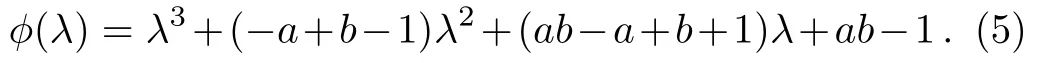
And when substituting the equilibrium pointE+orE−into expression(3),one gets As we know,characteristic equations(4)and(5)are irrespective to parametersf,g,h,that is,the characteristic roots remain unchanged whenf,g,hvary in the field of real number,proving that the Lyapunov exponent spectrum remains constant.This completes the proof.

Remark 1Wheng=h=constant,the coefficientfmodulates the signal amplitude of variablesx1,x2,x3according torespectively.And the Lyapunov exponent spectrum remains constant whenfvaries.As diagramed in Fig.3.

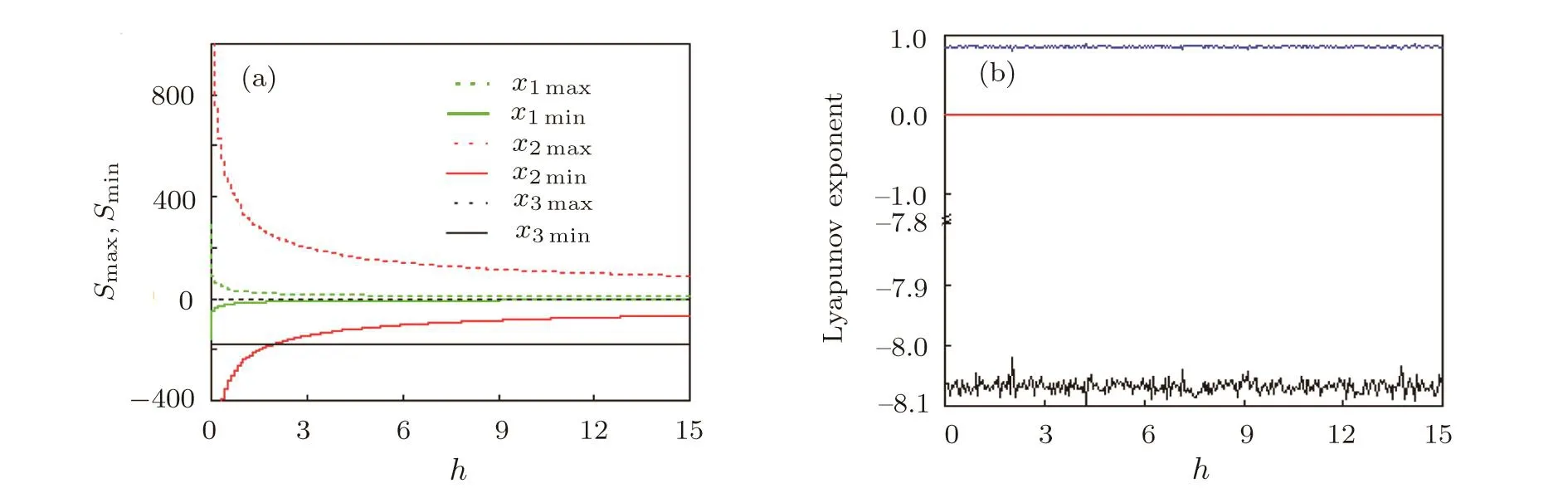
Fig.3 (a)Signal amplitude and(b)Lyapunov exponent spectrum versus f.

Remark 2Whenf=h=constant,the coefficientgmodulates the signal amplitude of variablesx1,x2,x3accordingrespectively,with constant Lyapunov exponent spectrum.The corresponding iconography is displayed as Fig.4.

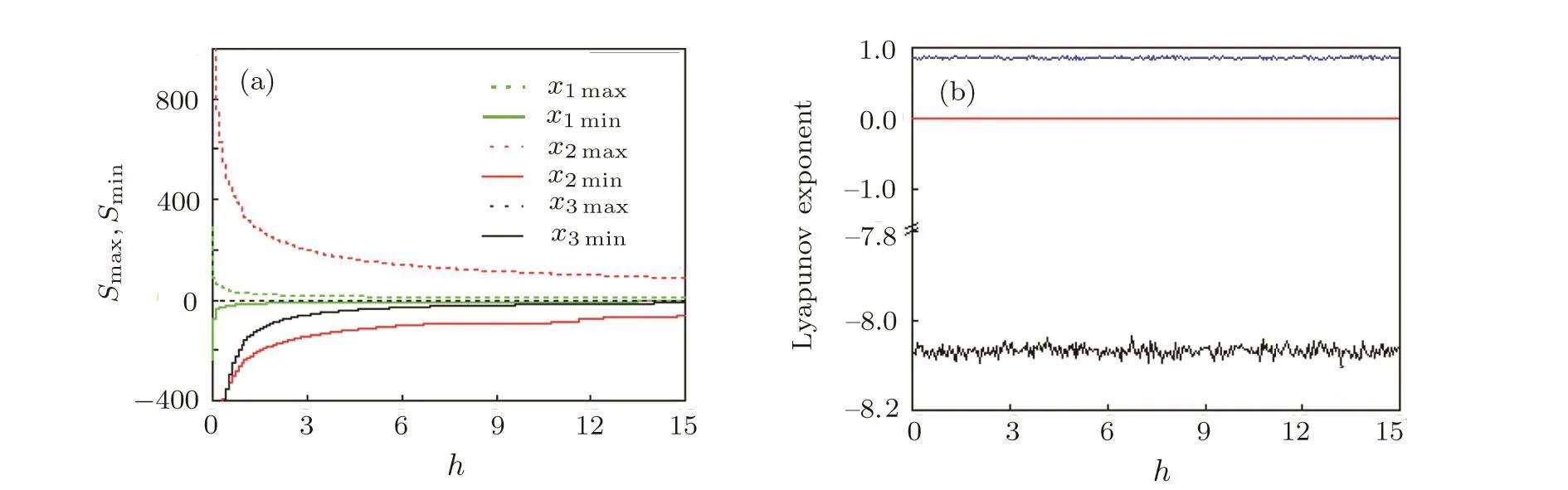
Fig.4 (a)Signal amplitude and(b)Lyapunov exponent spectrum versus g.

Remark 3Whenf=g=constant,the coefficienthmodulates the signal amplitude of variablesx1,x2accordingrespectively,while the signal amplitude ofx3is unchanged,with constant Lyapunov exponent spectrum.As displayed in Fig.5.

Remark 4One can obtain different modulation type for the amplitude of output variables by fl exibly selecting and combining modulation coefficient.For example,let the control parameter ask,andf=h=k,g=k−2,then control parameterkmodulates the signal amplitude of variablesx2,x3according to 1/k,k,respectively,while the signal amplitude ofx1is unchanged.

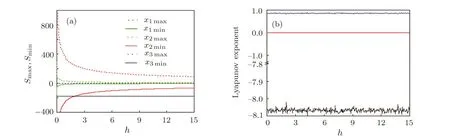
Fig.5 (a)Signal amplitude and(b)Lyapunov exponent spectrum versus h.

Remark 5When conditionfgh>0 is met,the productfgcan modulate the signal phase ofx3.That is to say,the polarity of signalx3changes with the one of productfg.The phase reversal can also be seen from the invariance under the coordinate transformation(x1,x2,x3,a,b,f,g,h)→(x1,x2,−x3,a,b,f,−g,−h)or(x1,x2,x3,a,b,f,g,h)→(x1,x2,−x3,a,b,−f,g,−h).Two different cases are depicted in Figs.6(a)and 6(b),respectively.In Fig.6(a),the transformationfg→−fgonly leads to the phase reversal ofx3.But in Fig.6(b),the amplitude modulations ofx1andx2are obtained besides phase reversal ofx3.

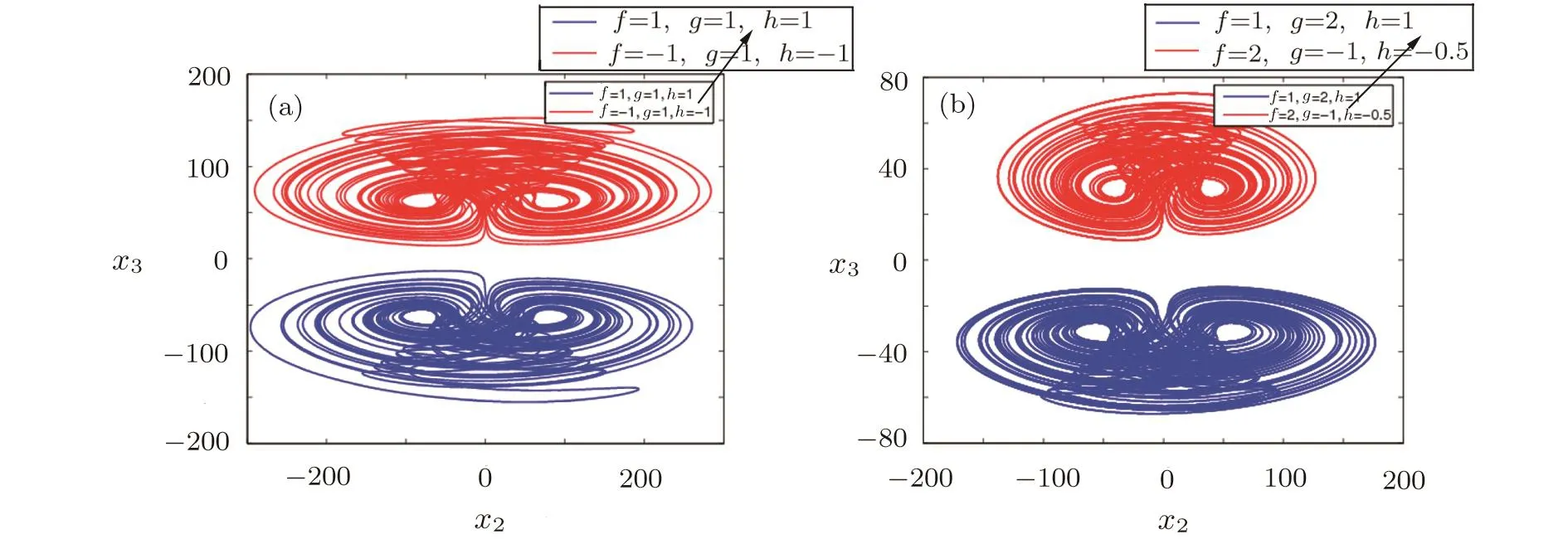
Fig.6 (Color online)Phase reversal of x3when(f,g,h)equals to(a)(1,1,1)in red,(−1,1,−1)in blue;(b)(1,2,1)in red,(2,−1,−0.5)in blue.

4 Topological Horseshoe of System(1)

4.1 Topological Horseshoe Theory

In this section,we recall the topological horseshoe theory of dynamical system.[20,22]

LetSm={1,2,...,m}be the set of non-negative integer from 1 tom,andRmbe the collection of all unilateralin finite sequences with elementSm,i.e.,s∈Rmimpliess={s1,s2,...,sm,...},si∈Sm.If we consider another sequence˜s(˜si∈Sm),then the distance betweensand˜sis defined as below

With the exact definition as above equation,Rmis a Cantor set with the properties of compact,totally disconnected and perfect.

Anm-shift mapσ:Rm→Rmis defined as

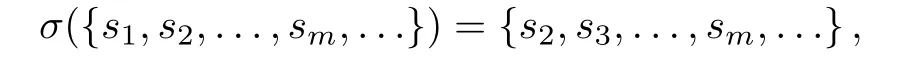
which possesses the following properties:(i)An uncountable in fi nity of non-periodic orbits;(ii)A countable in fi nity of periodic orbits consisting of orbits of all periods;(iii)A dense orbit.The dynamics generated by the shift mapσdepend sensitively on the initial conditions,therefore are chaotic.

LetSbe a separable metric space,Qbe a compact subset ofS,andf:Q→Sis a map satisfying thatQ1,Q2,...,Qmaremmutually disjoint compact subsets ofQ.f|Qiis continuous for eachQi.

Definition1[20,22]Suppose,⊂Qi(1≤i≤m)be two fixed disjoint compact subsets.We say a connected subsetγofQiconnectand,ifγ∩ndγ∩are compact and nonempty,and we denote it byDe finition 2[22]Letγbe a connected subset ofQi,f(γ)is called to suitably acrossQiwith respect toandif there exists a connected subsetγi⊂γsuch thatf(γi)⊂Qi,andf(γi)∩,f(γi)∩are nonempty.And we denote this byf(γ)7→Qi.

De finition 3For topological spacesRmandS,continuous functionsg:Rm→Rmandf:S→S,if there is a continuous surjectionh:Rm→Ssuch thatf◦h=h◦g,we say thatfis topologically semi conjugate tog.

Theorem 2[22]Iffu(Q1)7→Q1,fu(Q1)7→Q2,fv(Q2)7→Q1andfv(Q2)7→Q2,then there exists a compact invariant set Λ⊂Q,such thatfu+v|Λ is semi conjugate to 2-shift dynamics,and the topological entropy offsatisfies ent(f)≥[1/(u+v)]log2.

4.2 Topological Horseshoe of System(1)

We will present a rigorous veri fi cation of chaos in the proposed system(1)following the idea in Ref.[22].To study the horseshoe of system(1)with parametersa=10,b=6,f=1,g=1,h=1,we consider the crosssection plane∏:x1=0.And in the plane,we take a quadrilateralPwith four vertices being(0,−180,−160),(0,0,−160),(0,0,−20),(0,−180,−20),as shown in Fig.7.

First,after many attempts,we find a subsetQ1ofsectionP, with the four vertices (0, –97.769,−60.099),(0,–95.985,–63.092),(0,–111.152,–91.521),(0,−112.936,−87.032).Letandbe the right and left sides ofQ1.The computer simulation(see Fig.8(a))shows that under the first return mapH1,H1()lies on the left side ofH1()lies on the right side ofwhich implies the imageH1(x)(x∈Q1)suitably across the quadrangleQ1.

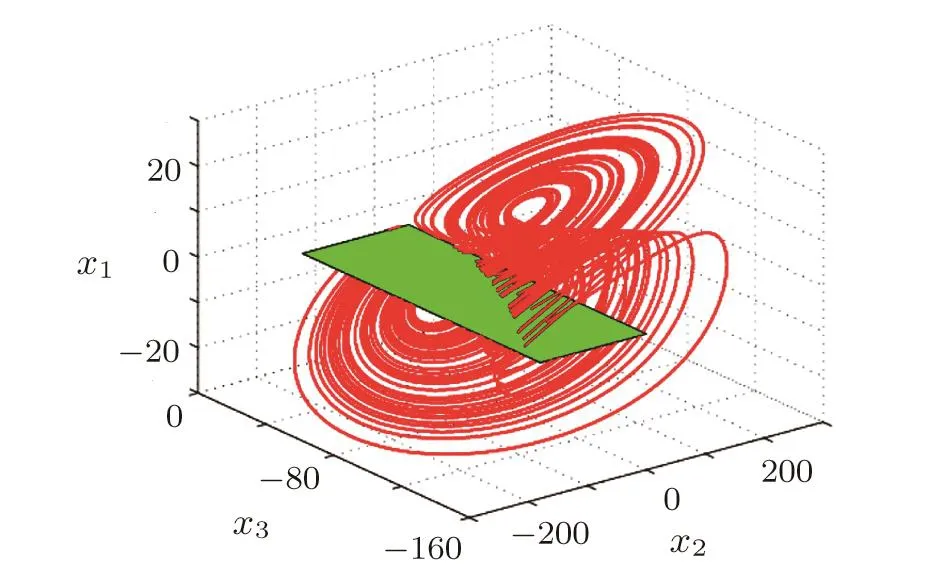
Fig.7 Poincar´e cross-section of system(1).

Fig.8 (a)The subset Q1and its image;(b)The subset Q2and its image.

Secondly,we select another subsetQ2of sectionPwith vertexes(0,–116.803,–107.1821),(0,–121.323,–98.2045),(0, –131.316, –116.758),(0,−125.606,−123.342),such thatH(Q1)7→Q2,H(Q2)7→Q2andH(Q2)7→Q1.Analogously,supposeandbe two sides ofQ2,respectively.SinceH1()lies on the right side of,H1()lies on the left side of.Therefore,we can conclude that the first return Poincar´e mapH1(x)(x∈Q2)is wholly across the quadrangleQ1andQ2,as displayed in Fig.8(b).

It follows from Theorem 2 that there exists a compact invariant set Λ⊂Q,such thatH2|Λ is semi conjugate to a 2-shift dynamics,and we have ent(H)≥0.5·log2.This fact proves that the attractor illustrated in Fig.7 has positive topological entropy,therefore it is chaotic.

5 Scaling Attractor of System(1)

5.1 Synchronization Scheme

Taking full account of the amplitude and phase modulation property,the scaling chaotic attractors of the proposed system are studied here,and some new results are obtained.

Based on the modified projective synchronization scheme,the corresponding drive-response systems are expressed,respectively,as

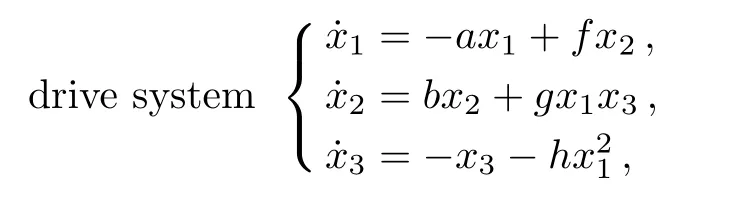
whereuis the controller,parameters(f,g,h)in drive system and(f′,g′,h′)in response system may be different to regulate the scaling factor.

Let the synchronization errors as

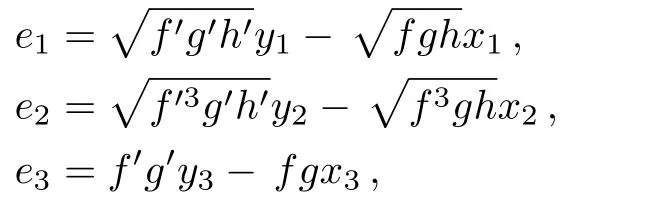
then the error dynamical system reads

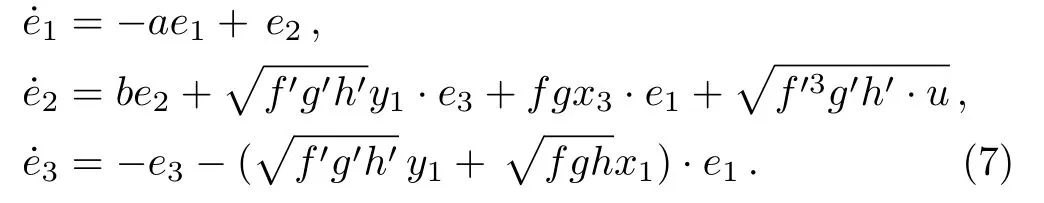
Theorem 3The modified projective synchronization between drive-response systems in Eq.(6)can be realized when the single controller is designed asu=−ke2,wherekis control strength satisfyingand the scaling factors can be remark as

ProofFor the error dynamical system(7),we construct the following candidate Lyapunov function

Taking the time derivative ofValong the synchronization error leads to

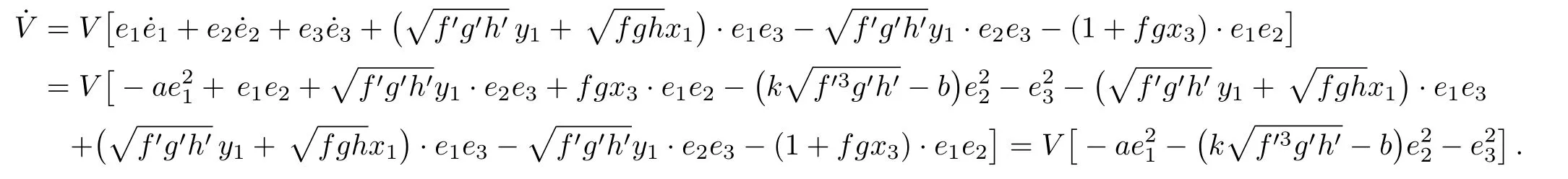
According to the Lyapunov stability theory,the orbits of the error system(7)will converge asymptotically to the set(e1,e2,e3)=(0,0,0)with certain transient period and thus the drive-response systems in Eq.(6)become synchronized only since the conditionsV>0 and˙V<0 underk≥kcare satisfied completely.This completes the proof.

The introduced synchronization scheme is simpler and more applicable because it only holds a single linear coupling controller.And since the scaling factors in projective synchronization are determined only by the system parameters and can be regarded as the key,this scheme may be safer for real-time encryption and decryption in secure communications than the existed synchronization method.[27−29]

Generally speaking,increased control strengthkwill bring on shorter transient period of synchronization and yet larger instantaneous power of controller. Spontaneously,we will consider the significant issue on the variation tendency of the total control consumption with coupling strengthk.For synchronization scheme in Eq.(6),the total energy consumption for the controller can be evaluated by the integral representation of synchronization error,depicted as

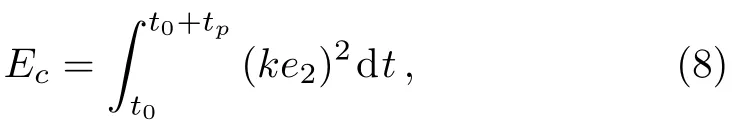
wheret0is the initial time for controller inputting,andtpdenotes the transition period of synchronization.

As we know from Eq.(8)that the total control cost depends on the coupling strengthk. In order to realize modified projective synchronization between driveresponse systems in Eq.(6)with best quality,we attempt to find an optimal coupling strengthkto minimize the total energy consumption of the controller.This handling way means that the appropriate parameterkis found to minimize the performance index(8)with shortest possible transient time.

5.2 Numerical Simulation and Analysis

In this subsection,two numerical examples are taken into account to achieve MPS with different scaling factors,the initial conditions for drive and response systems are chosen asx(0)=(−1,1,−1),y(0)=(2,0.5,1).

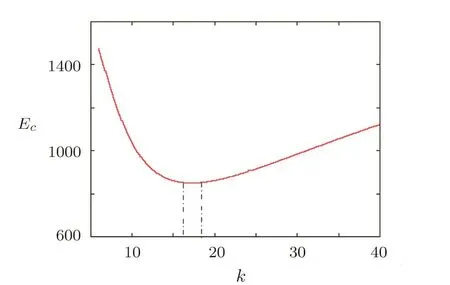
Fig.9 Energy consumption Ecversus coupling strength k with a=10,b=6,f=1,g=4,h=1,f′=1,g′=1,h′=1.

First,we select system parametersa=10,b=6,f=1,g=4,h=1,f′=1,g′=1,h′=1.The critical coupling strength is calculated askc=6,which may not be the optimal parameter.The relation of energy consumptionEcdepending onkis depicted in Fig.9.It shows when parameterkis slowly increased,Ecdecreases first,then increases gradually.We find with a detailed observation that the energy consumptionEcremains invariable whenk∈[16.5,18].Therefore,when selectingk=kopt=18,one can realize MPS of drive-response systems in Eq.(6)with lowest control consumption and shortest possible transient time.The corresponding simulation results for MPS are presented in Fig.10.It is known that the proposed control scheme provides the scaling factorsα1=2,α2=2,α3=4.

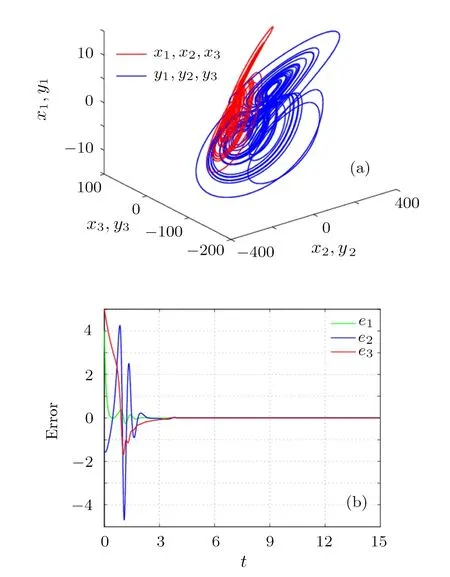
Fig.10 Scaling attractor obtained by MPS with a=10,b=6,f=1,g=4,h=1,f′=1,g′=1,h′=1,k=18.(a)chaotic attractors;(b)errors evolution.

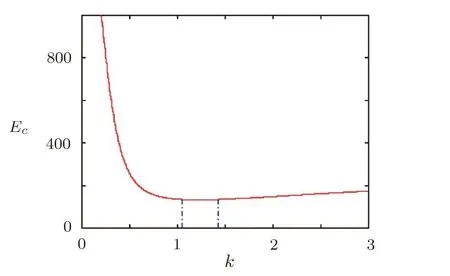
Fig.11 Energy consumption Ecversus k with a=10,b=6,f=1,g= −1,h= −64,f′=4,g′=4,h′=1.

Then,with the selection of system parametersa=10,b=6,f=1,g=−1,h=−64,f′=4,g′=4,h′=1,the critical coupling strength is calculated askc=0.375.As described in Fig.11,the total energy consumptionEcdecreases when 0.375≤k<1.1,keeps almost invariable when 1.1≤k≤1.35,then increases slowly withk>1.35.Therefore,to achieve MPS of the drive-response systems in Eq.(6)with lowest control cost and shortest possible transient time,the optimal control parameter isk=1.35,as depicted in Fig.12.It is shown that the proposed control scheme provides the scaling factorsα1=2,α2=1/2,α3=−1/16.In particular,the phase difference between two attractors withx3isπ.

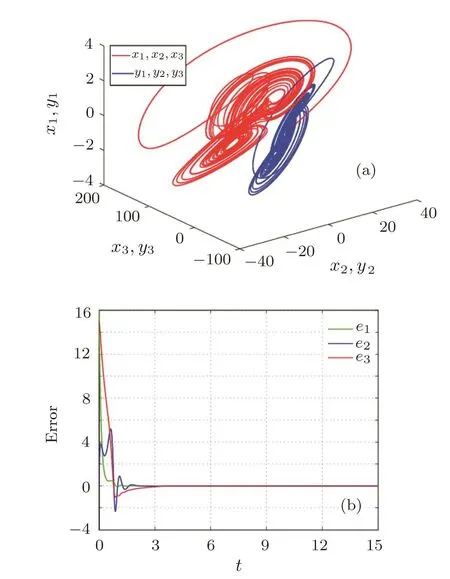
Fig.12 Scaling attractor obtained by MPS with a=10,b=6,f=1,g= −1,h= −64,f′=4,g′=4,h′=1,k=1.35.(a)chaotic attractors;(b)errors evolution.

6 Conclusion

Amplitude and phase modulation of chaotic system are important in engineering and technological applications.To the best of our knowledge,however,the issue of amplitude and phase modulation received only moderate attention and there have been few results in the literature so far.Therefore,it still remains open and challenging.

In this paper,a three-dimensional autonomous chaotic system with quadratic nonlinearities is considered.The main property of the system we found through this study is that the coefficients of linear term,cross-product term and squared term can be simultaneously or respectively employed to modulate the signal amplitude,and the phase ofx3can be modulated by the coefficient product of the linear term and cross-product term.But in Refs.[15–19],only the coefficient of nonlinear term or the coefficient of single linear term can be provided to modulate the signal amplitude.And it is known to us from the existed result that the phase reversal parameter is only one of the coefficients of nonlinear term.[16]The comparative analyses show that the type of amplitude-phase modulation can be well designed by fl exibly combining different coefficients,which will greatly enhance the potential application of the present system in various disciplines of science and engineering.

Some basic dynamical properties of the system,including topological horseshoe,are studied in detail.Furthermore,scaling chaotic attractors of this system are achieved by modified projective synchronization with a single linear coupling controller.Based on the total energy consumption of the controller,the optimal coupling strength is determined numerically.The scaling factors can be regarded as the encoding key in synchronization process,which renders the proposed scheme greatly meritorious and safer to practical secure communications.

[1]E.N.Lorenz,J.Atmospheric Sci.20(1963)130.

[2]G.R.Chen and T.Ueta,Int.J.Bifurcat Chaos 9(1999)1465.

[3]J.H.Lü and G.R.Chen,Int.J.Bifurcat Chaos 12(2002)659.

[4]Z.C.Wei and Q.G.Yang,Nonlinear Anal.:RWA.12(2011)106.

[5]Z.H.Guan,Q.Lai,M.Chi,X.M.Cheng,and F.Liu,Nonlinear Dyn.75(2014)331.

[6]K.B.Deng,J.Li,and S.M.Yu,Optik 125(2014)3071.

[7]C.L.Mu,F.C.Zhang,Y.L.Shu,and S.M.Zhou,Nonlinear Dyn.67(2012)987.

[8]S.J.Cang,Z.H.Wang,Z.Q.Chen,and H.Y.Jia,Nonlinear Dyn.75(2014)745.

[9]P.YU and J.H.Lü,Int.J.Bifurcat Chaos 21(2011)2647.

[10]D.Kim and P.H.Chang,Results Phys.3(2013)14.

[11]D.Cafagna and G.Grassi,Commun.Nonlinear Sci.Numer.Simul.19(2014)2919.

[12]C.L.Li and Y.B.Zhao,Commun.Theor.Phys.63(2015)317.

[13]B.Muthuswamy and L.O.Chua,Int.J.Bifurcat Chaos 20(2010)567.

[14]V.Sundarapandian and I.Pehlivan,Math.Comput.Model.55(2012)1904.

[15]C.L.Li,L.Wu,H.M.Li,and Y.N.Tong,Nonlinear Anal Model Control.18(2013)66.

[16]C.L.Li,K.L.Su,and L.Wu,J.Comput Nonlinear Dynam.8(2013)031005.

[17]C.L.Li,K.L.Su,and J.Zhang,Appl.Math.Model 39(2015)5392.

[18]M.S.Abdelouahab and N.E.Hamri,Nonlinear Dyn.67(2012)457.

[19]C.B.Li and J.C.Sprott,Phys.Lett.A 378(2014)178.

[20]J.Kennedy,S.Kocak,and J.A.York,A Chaos Lemma.Amer.Math.Mon.108(2001)411.

[21]X.Yang,Int.J.Bifurcat Chaos.19(2009)1127.

[22]Q.Li and X.Yang,Int.J.Bifurcat Chaos.20(2010)467.

[23]H.Y.Jia,Z.Q.Chen,and G.Y.Qi,IEEE Trans.Circ.Syst.I.61(2014)845.

[24]C.Ma and X.Wang,Commun.Nonlinear Sci.Numer.Simulat.17(2012)721.

[25]C.L.Li,S.M.Yu,and X.S.Luo,Int.J.Bifurcat Chaos 23(2013)13501701.

[26]Q.J.Fan,Int.J.Bifurcat Chaos.22(2012)12502021.

[27]C.P.Li and W.H.Deng,Mod.Phys.Lett.B 20(2006)633.

[28]D.L.Xu,Z.G.Li,and S.R.Bishop,Chaos 11(2001)439.

[29]Q.G.Yang and C.B.Zeng,Commun.Nonlinear Sci.Numer.Simul.15(2010)4041.

[30]G.L.Wen,Nonlinear Dyn.63(2011)387.

[31]H.Xie and G.L.Wen,Commun.Nonlinear Sci.Numer.Simul.18(2013)3167.

[32]Y.G.Yu and H.X.Li,Nonlinear Anal.:RWA 11(2010)2456.

[33]Z.G.Li and D.L.Xu,Chaos,Solitons&Fractals 22(2004)477.

[34]S.E ff ati,J.Saberi-Nadja fi,and N.H.Saberi,Appl.Math.Model 38(2014)759.

[35]K.Z.Li,M.C.Zhao,and X.C.Fu,IEEE Trans.Circ.Syst.I.56(2009)2280.