Virial Coefficients from unified Statistical Thermodynamics of Quantum Gases Trapped under Generic Power Law Potential in d Dimension and Equivalence of Quantum Gases
2016-05-28ShahMohammadBahauddinandMirMehediFaruk
Shah Mohammad Bahauddinand Mir Mehedi Faruk∗
1Physics and Astronomy,Rice University,Houston,USA
2Theoretical Physics,Blackett Laboratory,Imperial College,London SW7 2AZ,United Kingdom
3Department of Theoretical Physics,University of Dhaka,Dhaka-1000,Banglagesh
1 Introduction
After the demonstration by Einstein[1−2]that there is a possibility of condensation of free bosons,bulk behavior of ideal free Bose gas are studied by many authors.[3−11]At the same time,theoretical investigations are also done for the free Fermi gas[12−16]and remarkable property of degeneracy pressure of the free fermions are noticed.[4]Dimensional dependence of the thermodynamic quantities of both types of ideal quantum gases are investigated in detail[3,10−11]and interesting dimensional dependence of thermodynamic quantities was reported.For instance,BEC is noticed in free Bose gas only whend>2,whether the specific heat is found discontinuous ifd≥4.But,it was May,[6]who first noticed an equivalence of specific heat for two-dimensional ideal free bosons and fermions.Later,Lee[17]generalized this equivalence between two-dimensional quantum gases for other thermodynamic quantities as well.It is reported in the paper that,one can obtain this equivalence,if the fugacities of Bose and Fermi gases are related by Euler transformation.[17−18]He also found a way to present the thermodynamic quantities of both of Fermi and Bose gases in a unified approach.Viefereset al.[19]showed that all the virial coefficients are equal in two-dimensional free quantum gases(except the second virial coefficients for which the signs are opposite).
The subject of quantum gases drew more attention after it was possible to experimentally detect BEC[20−22]and Fermi degeneracy[23]in trapped quantum gases.Since then,a lot of studies are done on Bose and Fermi gas trapped under generic power[24−31]law potential(U=in arbitrary dimension.Some drastic changes are noted in the characteristics of both Bose and Fermi gases due to trapping potential.[24−31]For instance,Bagnato and Kleppner demonstrated the possibility of BEC of an ideal Bose gas con fi ned by one-and two-dimensional power-law traps[32−33](d<3)with appropriate trapping potential,which is not a property of free Bose gas.[25,30]In addition,the equivalence of two dimensional free quantum gases do not remain valid for any trapping potential.[34]Very recently Mehedi[34]was able to present the thermodynamics of both types of quantum gases trapped under generic power law potential in a unified way.Remarkably an equivalence between them ind=1 was found for harmonically trapped systems.[34]Turning our attention towards virial coefficients,it would be intriguing to check if the virial coefficients become equal,for harmonically trapped quantum gases in one dimension.
Virial coefficients appear to relate the pressure of a many-particle system in powers of the number density in a givend-dimensional volume,providing a systematic treatment in the corrections of the laws of ideal gases.Thed-dimensional virial coefficients of quantum gases trapped under generic power-law potentials are not yet reported.In this paper,we have first calculated the virial coeffi-cients of both types of ideal quantum gases trapped under generic power law potentialin a unified approach in arbitrary dimension.But the main motivation of this investigation is to check out whether the virial coefficients of Bose and Fermi gases become same for when they are harmonically trapped ind=1.Now,from the more general result one should be able to reproduce the known solutions such as text book results of virial coefficients of bosons and fermions ind=3 and the outcome of Viefereset al.’s calculation relating virial coefficients of two-dimensional free Bose and Fermi gases.But more importantly,we would be able to find out,whether the virial coefficients are also the same for one-dimensional quantum gases trapped in a harmonic potential,suggesting the equivalence found by Mehedi.[34]
2 Virial Coefficients of Ideal Quantum Gases Trapped under Generic Power Law Potential
For a quantum gas,the average number of particles occupying thei-th single particle energy eigenstate and the grand potential are given by

where,a=−1(1)stands for a Bose systems(Fermi systems),zis the fugacity andβ=1/KTis the Boltzmann constant.Let us consider an ideal quantum system trapped in a generic power law potential ind-dimensional space with a single particle Hamiltonian of the form,

where,b,l,ai,ci,andniare all positive constants,pis the momentum andxiis thei-th component of the coordinates of a particle.Here,ci,ai,nidetermine the depth and con fi nement power of the potential,lis the kinematic parameter,andxi where,λ′andV′are the effective thermal wavelength and effective volume,††To read more about effective volume and effective thermal wavelength,see Refs.[26–27,29].and Liχ(σ)is the polylog function.Here, And a useful representation of polylog is[17] for Re(m)<1.And quantityχandσare, wherezis the fugacity.Now the density can be calculated from the grand potential, And the pressure, Now writing the pressure and density equation as series[4] where the coefficientsbjare defined as, Next we need to express the fugacity in terms of density so that one can write the pressure as a series of density.Writing the density equation explicitly, In the high temperature limit we can approximate fugacity, Puttingzinto the expressionλ′dρ, Now comparing Eqs.(15)and(17), So,one can establish relation betweenaiandbi, Now from the pressure equation, The virial expansion is defined as, where,Alare the virial coefficients.Thus comparing the above two equations we can calculate the virial coefficients, where,thebjare defined in Eq.(14). Point to note that,these results are quite general for ideal quantum gas trapped under generic power law potential.Depending upon boson or fermion as well as the type of trapping potential the virial coefficients,Eqa.(22)–(28)will change accordingly.Also,the result of Eqs.(22)–(25)coincides well with Ref.[25]. The results of virial coefficients presented in Eqs.(22)–(28)are for ideal quntum gases trapped under generic power law potential in any dimension.In this section we first present the fi nal results for some specific situation. We have later presented two tables containing the results of virial coefficients of bosons and fermions,trapped under different power law potentials. At first,we present the virial coefficients for the free massive bosons(l=2)in three-dimensional space.So,choosingd=3 and allni−→∞which leaves usχ=3/2.In this case Eqs.(22)–(28)dictates,the virial coefficients of bosons are, Turning our attention towards free massive Fermi gas in three-dimensional space,the virial coefficients are, The results of Eqs.(29)and(30)concur with Ref.[4].It is interesting to point out that,in the case of Fermi gases ind=3 the virial coefficients alters sign while all the virial coefficients of Bose gases are negative.Point to note,any negative(positive)virial coefficientAnindicates that,then-particle wave function is symmetric(asymmetric).As the bosonicn-particle wave function is always symmetric in three-dimensional space,we see the virial coefficients of bosons are negative.And as we know in three dimensions,thenparticle fermion wave functions(evenn)are anti-symmetric,Anare positive for evenn,ind=3.But anyn-particle Fermi wave function is symmetric ind=3 whilenis odd.So,we have found negative virial coefficientAn,for oddn.Thus we find out the reason due to which we get the alternating sign in virial coefficients of Fermi gas ind=3. Turning our focus on the virial coefficients of free massive quantum gases in lower dimensions we choosed=2 and allni−→∞,and find out thatχ=2. Equations(22)–(28)dictate the virial coefficients for bosons are, while the virial coefficients of fermions are, The results match precisely with the vieferset al.[19]Please note that,all the virial coefficients for Bose gases are equal to Fermi gases(except for the second virial coefficient,for which the signs are opposite).This important result turns out to indicate the equivalence of free Bose and Fermi gases in two dimension.[17]And the opposite signs of second virial coefficient indicate that,the only difference in pressures between free Fermi and Bose gases is the Fermi degeneracy pressure.[19]Also,note that all the even virial coefficients are zero afterA2.Both of these features are explained later,more carefully.But it is reported in Ref.[34]the equivalence found in two dimensional quantum gases is lost when they are trapped with potential.So,let us now turn our attention towards the virial coefficients of the trapped system. To see the effect of different trapping potential in the various dimension we introduce two tables presenting virial coefficients of Bose(Table 1)and Fermi gases(Table 2)below.In this case we have considered symmetric potential,i.e.n1=n2=···=nd=n.It is clear from the tables that the trapping potential greatly affects the virial coefficients. Table 1 Virial coefficients of ideal Bose gas trapped under power law potential in d dimension. Table 2 Virial coefficients of ideal Fermi gas trapped under power law potential d dimension. More importantly,it is seen in the tables that the virial coefficients of one-dimensional harmonically trapped Bose gases are equal to the one-dimensional harmonically trapped Fermi gases,except the second virial coefficients for which the signs are opposite.This outstanding property,ealier seen in two-dimensional free quantum gases,indicates the equivalence reported by Mehediet al.[34]Another intriguing behavior is the appearance of even virial coefficients being zero while there is an equivalence in Bose and Fermi gases are seen in this case,which is also found in two-dimensional free quantum gases only.And fi nally we point out the most remarkable property feature in the table,which is the virial coefficients of one-dimensional harmonically trapped quantum gases are being equal to the virial coefficients of two dimensional free system(both bosons and fermions).This phenomenon suggests high temperature behavior of two-dimensional free quantum gases(Bose and Fermi)is similar to one-dimensional harmonically trapped quantum gases(Bose and Fermi). (i)Equivalence of Harmonically Trapped Quantum Gases in d=1 It is very important to point out in both the cases where this equivalence of Bose and Fermi gases are noticed[34]takes the valueχ=1.Now,focusing over the harmonically trapped quantum gases in one dimension,we find the density of such quantum gases where,the upper sign is for fermions and the other is for boson.From this we can explicitly write the fugacity,which is The pressure equation leads us to Now using the techniques of partial derivative we get from the above two equations, Now the equation of state is thus given by, Notably this functional form can be expressed in terms of Bernoulli numbers,[19] where,0<|p|<2π.Bnare known as Bernoulli numbers and be defined as,[36] Again rewriting Eq.(21),choosingd=1 andn=2, Using the above equations we conclude virial coefficients in this case, Incidentally this is the same result obtained in two dimensional free quantum gas as well.[19]Now as odd Bernoulli numbersBnare zero except(n=1)we find out even virial coefficientsAnwill be zero for both Bose and Fermi gases,except(n=2).As it is seen from above beside the second virial coefficient,all the virial coefficients do become the same when there is an equivalence,let us focus on this phenomena in a more detail.The pressure for one-dimensional harmonically trapped quantum gases from Eq.(38), So,the difference in pressure of Bose and Fermi gas in this case is,Now,with harmonic trapping potentialV′∝T1/2andλ′∝T−1/2,the right hand side of the above equation is a temperature independent quantity.As it turns out it is nothing but the ground state pressure also known as degeneracy pressure in Fermi gases.[34]Similar situation is also observed in Ref.[19]in the case of two-dimensional free quantum gases.The reason of such phenomena is due to Landen relation of dilog functions,[17] where,x1andx2are related asx2=x1/(1−x1),known as Euler transformation.[18]As fugacities of Bose and Fermi gas can be connected as an Euler transformation Eqs.(10)and(11)dictate the relation described by Eq.(43) The virial coefficients of both types of ideal quantum gases trapped under generic power law potentials are calculated from unified statistical thermodynamics.The general results of this paper coincide with the known results[4,19]ind=2 andd=3 with appropriate choice ofni.The equivalence[17]of two-dimensional ideal free Bose and Fermi gases revealed a remarkable property[19]that their virial coefficient are same(except the second virial coefficient,where the sign is different).We further showed that,the recently established equivalence(ind=1)between the harmonically trapped ideal Bose and Fermi gases also maintains this property.Hence it can be concluded that,in both of the cases,where equivalence relation can be established between Bose and Fermi gas,bosons and fermions do carry identical virial coefficients.Also from the table,one can see that the virial coefficients of two-dimensional free quantum gases are identical to the virial coefficients of one-dimensional harmonically trapped quantum gases.This interesting result suggests that the high-temperature behavior of bosons and fermions in these two types of systems should be indistinguishable.Lastly,since the calculation in this paper is done in thermodynamic limit,the virial coefficients are yet to be done beyond the thermodynamic limit.We are currently doing this using Yukolov’s semiclassical approximation.[37]It will be equally intriguing to examine the behavior of virial coefficients for relativistic quantum gases by taking into account the effect of antiparticles. Acknowledgments M.M.Faruk would like to thank Md.Alamgir Al Faruqui for his cordial hospitality during MMF’s stay in London.Special thanks to Laura Alejiandra Moya Camacho to help MMF to present the manuscript. [1]S.N.Bose,Z.Physik 26(1924)178. [2]A.Einstein,Berl.Ber 22(1924)261. [3]R.M.Zi ff,G.E Uhlenbeck,and M.Kac,Phys.Rep.32(1977)169. [4]R.K.Pathria,Statistical Mechanics,Elsevier,Amsterdam(2004). [5]H.E.Haber and H.A.Weldon,Phys.Rev.Lett.46(1981)1497. [6]R.H.May,Phys.Rev.A 1515(1964)135. [7]J.E.Robinson,Phys Rev.E 83(1951)678. [8]E.H.Lieb and W.Liniger,Phys.Rev.130(1964)1605. [9]E.H.Lieb,Phys.Rev.130(1963)1606. [10]D.S.Fisher and P.C.Hohenberg,Phys.Rev.B 37(1988)4936. [11]R.Beckmann,F.Karch,and D.E.Miller,Phys.Rev.Lett.43(1979)1277. [12]C.M.Bender,S.Boettcher,and L.Lipatov,Phys.Rev.D 46(1992)5557. [13]C.M.Bender and S.Boettcher,Phys.Rev.D 51(1994)1875. [14]C.M.Bender and S.Boettcher,and L.R.Mead,J.Math.Phys.35(1994)368. [15]C.M.Bender and K.A.Milton,Phys.Rev.D 50(1994)6547. [16]C.Grosche and F.Steiner,J.Math.Phys.36(1995)2354. [17]M.H.Lee,Phys.Rev.E 55(1997)1518. [18]M.H.Lee,Acta Phys.Polonica 40(2009)1279. [19]S.Viefers,F.Ravndal,and T.Haugset,American Journal of Physics 63(1995)369,doi:10.1119/1.17922. [20]C.C.Bradley,C.A.Sackett,J.J.Tollett,and R.G.Hulet,Phys.Rev.Lett.75(1995)1687. [21]M.H.Anderson,J.R.Esher,M.R.Mathews,C.E.Wieman,and E.A.Cornell,Science 269(1995)195. [22]K.B.Davis,M.O.Mewes,M.R.Andrew,N.J.Van Druten,D.S.Durfee,D.M.Kurn,and W.Ketterle,Phys.Rev.Lett.1687(1995)75. [23]B.DeMarco and D.S.Jin,Science 285(1999)1703. [24]S.Biswas,J.Mitra,and S.Bhattacharyya,J.Stat.Mech.P 03013(2015)15. [25]Luca Salasnich,J.Math.Phys.41(2000)8016. [26]Z.Yan,Phys.Rev.A 59(1999)4057. [27]Z.Yan,Phys.Rev.A 61(2000)063607. [28]Z.Yan,Ming-Zhe Li,L.Chen,C.Chen,and J.Chen,J.Phys.A:Math.Gen.32(1999)4069. [29]Z.Yan,Eur.J.Phys.21(2000)625. [30]M.M.Faruk and G.M.Bhuiyan,Acta Physica Polonica B 46(2015)12. [31]M.M.Faruk,Acta Phys.Polonica B 46(2015)12. [32]V.Bagnato and D.Kleppner,Phys.Rev.A 44(1991)7439. [33]W.S.Dai and M.Xie,Phys.Rev.A 67(2003)027601. [34]M.M.Faruk,J.Stat.Phys.DOI 10.1007/s10955-015-1344-4. [35]Kazumoto Iguchi,Mod.Phys.Lett.B 11(1997)765. [36]M.Abramowitz and I.A.Stegun,eds.Handbook of Mathematical Functions with Formulas,Graphs,and Mathematical Tables,9th Printing,Dover,New York(1972)pp.804-806. [37]V.I.Yukalov,Phys.Rev.A 72(2005)033608.






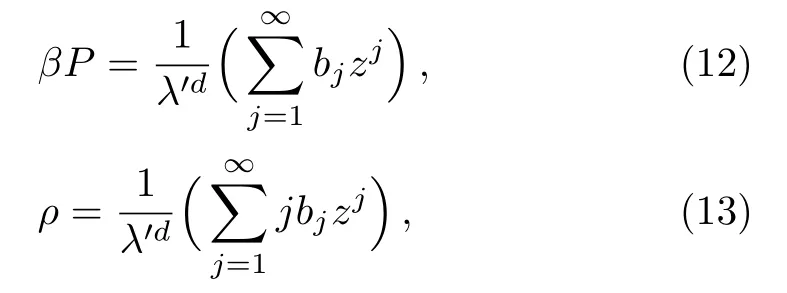
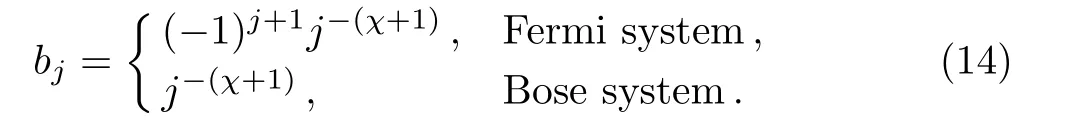



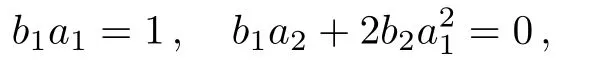
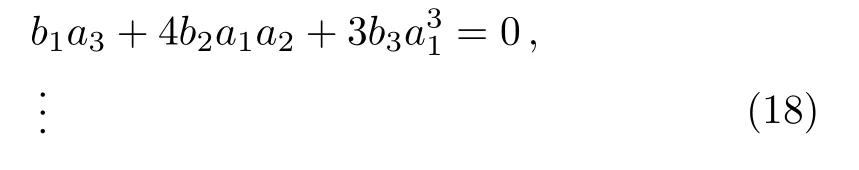





3 Results
3.1 Free Quantum Gases in d=3


3.2 Free Quantum Gases in d=2

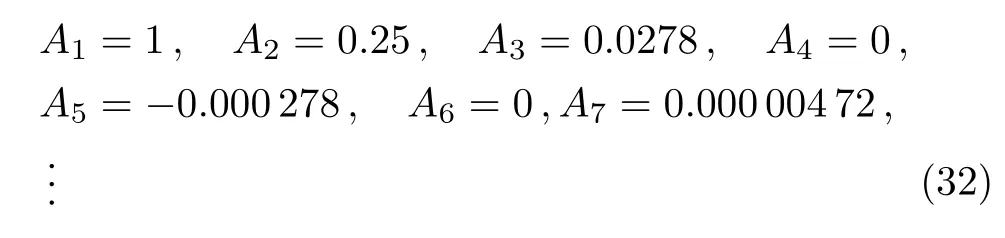
3.3 Effect of Trapping Potential on Virial Coefficients




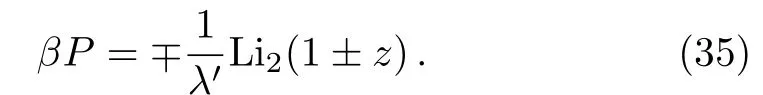





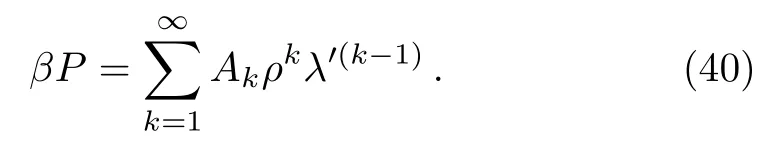


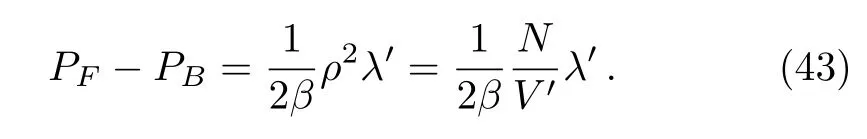

4 Conclusion
杂志排行
Communications in Theoretical Physics的其它文章
- Self-Focusing/Defocusing of Chirped Gaussian Laser Beam in Collisional Plasma with Linear Absorption∗
- Stationary Probability and First-Passage Time of Biased Random Walk∗
- Analysis of X(5568)as Scalar Tetraquark State in Diquark-Antidiquark Model with QCD Sum Rules∗
- A Three Higgs Doublet Model for Fermion Masses∗
- Lie Symmetry Analysis,Conservation Laws and Exact Power Series Solutions for Time-Fractional Fordy–Gibbons Equation∗
- Critical Behaviors and Finite-Size Scaling of Principal Fluctuation Modes in Complex Systems∗
