Multi-Party Quantum Private Comparison Protocol Based on Entanglement Swapping of Bell Entangled States∗

Tian-Yu Ye(叶天语)

College of Information and Electronic Engineering,Zhejiang Gongshang University,Hangzhou 310018,China

1 Introduction

Secure multi-party computation(SMPC),which was first introduced by Yao[1]in the millionaire problem,is a basic and important topic in classical cryptography.In Yao’s millionaire problem,two millionaires wish to know who is richer under the condition of not revealing the genuine amount of asset to each other.Afterward,Boudotet al.[2]constructed an equality comparison protocol to judge whether two millionaires are equally rich.SMPC can be applied into many scenarios such as private bidding and auctions,secret ballot elections,e-commerce,data mining and so on.

As a particular branch of SMPC,classical private comparison(CPC)aims to determine whether two secret inputs from different users are equal or not without disclosing their genuine values.With the development of quantum technology,CPC has been extensively generalized to its quantum counterpart,i.e.,quantum private comparison(QPC),whose security is based on the quantum mechanics principles rather than the computation complexity.However,Lo[3]pointed out that in a two-party scenario,the equality function cannot be securely evaluated.Under this circumstance,some additional assumptions,for example,a third party(TP),are needed.

The first QPC protocol was proposed by Yanget al.[4]using Einstein–Podolsky–Rosen(EPR)pairs with the help of one TP.In the same year,Yanget al.[5]proposed the QPC protocol with single photons.The security of these two protocols are essentially based on the one-way hash function.In 2010,Chenet al.[6]designed the QPC protocol with Greenberger–Horne–Zeilinger(GHZ)states.In 2012,Tsenget al.[7]constructed a novel QPC protocol with EPR pairs.In these two protocols,the secret inputs from two users are encrypted with the one-time-pad keys derived from the single-particle measurements.In 2012,Liuet al.[8]proposed the QPC protocol based on entanglement swapping of Bell states(hereafter,this protocol is called as LWC-QPC protocol).In this protocol,the secret inputs from two users are encrypted with the one-time-pad keys derived from the Bell-basis measurements after entanglement swapping of the original Bell states.However,Liuet al.[9]pointed out that in the protocol of Ref.[8],the TP can extract the two users’secret inputs without being detected by launching the Bell-basis measurement attack,and suggested an improved protocol(hereafter,this improved protocol is called as LLCLL-improved-QPC protocol).Up to now,besides the protocols mentioned above,many other two-party QPC protocols[10−34]have also been designed with different quantum states and quantum technologies.

As to the role of TP,Chenet al.[6]first introduced the semi-honest model.That is,TP executes the protocol loyally,records all its intermediate computations but might try to reveal the users’secret inputs from the record under the limit that he cannot conspire with the adversary including the dishonest user.However,Yanget al.[12]pointed out that this model of semi-honest TP was unreasonable and thought that the reasonable one should be in the following way:TP is allowed to misbehave on his own and also cannot be corrupted by the adversary in-cluding the dishonest user.In fact,up to now,this kind of assumption for TP is the most reasonable one.

Suppose that there areKusers,each of whom has a secret input.They want to know whether theirKsecret inputs are equal or not without disclosing them.If the twoparty QPC protocol is adopted to solve this multi-party equality comparison problem,the same two-party QPC protocol has to be executed withK−1∼K(K−1)/2 times so that the efficiency is not high enough.In 2013,Changet al.[35]proposed the first multi-party quantum private comparison(MQPC)protocol withn-particle GHZ class states,which can accomplish arbitrary pair’s comparison of equality amongKusers within one execution.Subsequently,the MQPC protocol based ond-dimensional basis states and quantum fourier transform,[36]and the MQPC protocol based onn-level entangled states and quantum fourier transform[37]were constructed.However,there are still few MQPC protocols until now.

In this paper,after carefully investigating the LLCLL-improved-QPC protocol,we find out that it still has an information leakage problem toward TP.Then we suggest an improved strategy for this loophole.We further put forward the three-party QPC protocol also based on entanglement swapping of Bell entangled state and generalize it into the multi-party case accordingly.

2 Review of the LLCLL-Improved-QPC Protocol

For integrity,in this section,a brief review of the LLCLL-improved-QPC protocol is given.

Alice and Bob have two secret integers,XandY,respectively,where here,xj,yj∈{0,1}.They want to know whetherXandYare equal or not with the help of a semi-honest TP.

The LLCLL-improved-QPC protocol can be depicted in the following way:

Step 1Alice/Bob divides her/his binary representation ofX/Yinto「L/2」groups

where each group contains two binary bits.IfLmod 2=1,one 0 should be added toby Alice/Bob.

Step 2Alice/Bob/TP prepares「L/2」quantum states all in the state of|ϕ+＞A1A2/|ϕ+＞B1B2/|ϕ+＞T1T2.Afterward,Alice/Bob/TP picks out the first particle from each state to form an ordered sequenceThe remaining second particle from each state automatically forms the other ordered sequence

Step 3∗Alice/TP preparesL′decoy photons randomly in one of the four statesto form sequenceDA/DT.Then,Alice/TP randomly insertsDA/DTintoto obtainAfterward,Alice and TP exchangebetween them.To check the security of the TP-Alice channel,Alice and TP implement the following procedures after Alice receives:(i)TP tells Alice the positions and the measurement bases of decoy photons in;(ii)Alice uses the measurement bases TPtold to measure the decoy photons inand informs TP of her measurement results;(iii)TP computes the error rate by comparing the initial states of the decoy photons in with Alice’s measurement results.If the error rate is low enough,they will continue the next step and Alice will drop out the decoy photons in;otherwise,they will halt the communication.

Step 4Forj=1,2,...,「L/2」,Alice performs the Bellbasis measurement on each pair inand obtains the corresponding measurement resultConsequently,the corresponding pair inin TP’s hands is collapsed into one of the four Bell states.These「L/2」collapsed Bell states in TP’s hands are denoted by

Step 5∗Bob preparesL′decoy photons randomly in one of the four statesto form sequenceDBand randomly insertsDBintoto obtainThen,Bob and TP exchangebetween them.After TP receives,TP and Bob check the security of the Bob-TP channel with the same method as that in Step 3∗.On the other hand,after Bob receives,Bob makes one-time eavesdropping check for the Alice-TP channel and the TP-Bob channel with Alice by checking the decoy photons in.If all quantum channels are secure,Bob and TP will discard the decoy photons and continue the next step.

Step 6Forj=1,2,...,「L/2」,Bob performs the Bellbasis measurement on each pair inand obtains the corresponding measurement resultConsequently,the corresponding pair inin TP’s hands is collapsed into one of the four Bell states.TP also performs the Bell-basis measurement on each pairand obtains the corresponding measurement resultthen

Step 7Forj=1,2,...,「L/2」,Alice and Bob calculateand sendRjto TP.Then,TP calculatesWithout loss of generality,we assume that Alice needs to send the result ofto Bob for calculatingRj.

Step 8TP sendsRto Alice and Bob.IfR=0,Alice and Bob conclude thatX=Y;otherwise,they know thatX=Y.

Note that the LLCLL-improved-QPC protocol only makes change for Steps 3 and 5 of LWC-QPC protocol.Steps 1,2,4,6,7,and 8 of LWC-QPC protocol are kept unchanged.

3 Information Leakage Problem and Corresponding Improvement

In this section,we first point out the information leakage problem in the LLCLL-improved-QPC protocol in Subsec.3.1,then suggest the corresponding improvement in Subsec.3.2.

3.1 Information Leakage Problem

The protocol involves many different parameters,including Alice’s two-bit inputBob’s two-bit inputAlice’s measurement resultthe coding of Alice’s measurement resultBob’s measurement result,the coding of Bob’s measurement result,TP’s measurement result,the coding of TP’s measurement resultthe result ofthe result of

lations among these different parameters whenare listed in Table 1(see Appendix).It is easy to find out thattotally has three different kinds of value,i.e.,0,1 and 2.When=0,we haveotherwise,it followsAfter deducing all the relations among these different parameters when=01,=10 and=11,respectively,we can further summarize the relations betweenand,which are shown in Table 2(see Appendix).From Table 2,it is easy to know that when=0,()may be(00,00),(01,01),(10,10)or(11,11);when=1,()may be(00,01),(01,00),(10,11),(11,10),(00,10),(01,11),(10,00)or(11,01);and when=2,(,)may be(00,11),(01,10),(10,01)or(11,00).Furthermore,when=,there are totally four kinds of(,);and when,there are totally twelve kinds of().As a result,when=1,the eight possible kinds of()include 3 bits for TP,which means that log23−1 bit information has been leaked out to TP;and when=2,the four possible kinds of(,)include 2 bits for TP,which means that log23 bit information has been leaked out to TP.This protocol has an information leakage problem toward TP indeed.

3.2 Corresponding Improvement

In order to avoid the information leakage problem toward TP,we should make TP get nothing aboutandwhenIn this Subsection,we give an improvement to mend this loophole.In order to retain the main features of the LWC-QPC protocol,we make as few modifications as possible.The LWC-QPC protocol should be modified as follows:

Step1#Similar to the QPC protocols of Refs.[4–5],Alice and Bob share a secret one-way hash functionHin advance.Here,the one-way hash function is defined as:H:{0,1}L→{0,1}N,whereLis the length of the secret inputs andNis the length of the hash values of the secret inputs.The hash values ofXandYarerespectively. Alice/Bob divides her/his binary representation ofX#/Y#into「N/2」groupwhere each group contains two binary bits. IfNmod2=1,one 0 should be added toby Alice/Bob.

Step 2#Alice/Bob/TP prepares「N/2」quantum states all in the state ofAfterward,Alice,Bob and TP do the same thing as that in Step 2 of the LWC-QPC protocol.

Step 3#,4#,5#and 6#These Steps here are the same as those of the LWC-QPC protocol.

Step 7#Forj=1,2,...,「N/2」,Alice and Bob calcu-

Rjto TP.Then,TP calculatesWithout loss of generality,we assume that Alice needs to send the result ofto Bob for calculatingRj.

Step 8#This Step here is the same as that of the LWCQPC protocol.

Compared with the LWC-QPC protocol,in the above improvement,we add the encryption process for Alice and Bob’secret inputs with a one-way hash function to enhance their privacy.Similar to the LWC-QPC protocol,in the above improvement,TP can also obtain the relations betweenwhich are shown in Table 3(See appendix).However,the one-way property of the hash function can guarantee that knowingandis still helpless to deduceAs a result,TP cannot get the relations betweenwhen.Therefore,none of information about Alice and Bob’secret inputs have been leaked out to TP whenIt can be concluded that using a one-way hash function to encrypt Alice and Bob’secret inputs beforehand helps overcome the information leakage problem toward TP.

It should be further emphasized that in order to retain the main features of the LWC-QPC protocol as many as possible,the above improvement still adopts the same eavesdropping check methods to those used in the LWCQPC protocol.Because the encryption process for Alice and Bob’secret inputs with a one-way hash function can automatically resist the Bell-basis measurement attack from TP suggested by Liuet al.,[9]it is not necessary for the above improvement to employ the decoy photon eavesdropping check methods any more.

4 Three-Party QPC Protocol Based on Entanglement Swapping of Bell Entangled States

In this section,by utilizing the above analysis,we suggest the three-party QPC protocol based on entanglement swapping of Bell entangled states in Subsec.4.1 first,then analyze its correctness and security in Subsec.4.2.

4.1 Three-Party QPC Protocol

Alice,Bob and Charlie have three secret integers,X,YandZ,respectively,whereThey want to know whether every two ofX,Y,andZare equal or not with the help of a semi-honest TP.They achieve the equality comparison of every two secret integers by implementing the following steps.Step 1 Preparation

(a)Similar to the QPC protocols of Refs.[4–5],Alice,Bob and Charlie share a secret one-way hash functionHin advance.The hash values ofX,YandZrespectively.Alice/Bob/Charlie divides her/his/her binary representation ofX#/Y#/Z#into「N/2」groupswhere each group contains two binary bits.IfNmod 2=1,one 0 should be addedby Alice/Bob/Charlie.

(b)Alice/Bob/Charlie/TP prepares「N/2」quantum states all in the state ofthe first particle from each state to form an ordered sequenceThe remaining second particle from each state automatically forms the other ordered sequence

(c)For the security check,Alice/TP prepares a sequence ofL′quantum states all in the state ofagain,which is denoted asDA′/DT′.Then Alice/TP inserts the first and the second particles of each Bell state inDA′/DT′intoat the same positions,respectively.Accordingly,Alice/TP obtainsThen,Alice and TP exchangetween them.To ensure the transmission security of Alice-TP/TP-Alice quantum channel,the entanglement correlation between two different particles of each Bell state inDA′/DT′is used to check whether there is an eavesdropper or not.If there is no eavesdropper,Alice and TP drop out the sample particles,and implement the next step.

(d)Forj=1,2,...,「N/2」,Alice performs the Bellbasis measurement on each pair inand obtains the corresponding measurement resultIfissequently,the corresponding pair inin TP’s hands is collapsed into one of the four Bell states.These「N/2」collapsed Bell states in TP’s hands are denoted by

Step 2The First Round Comparison

(a)Bob/TP prepares a sequence ofL′quantum states all in the state of|ϕ+＞to guarantee the security for the exchange ofandIf there is no eavesdropper,Bob and TP drop out the sample particles,and implement the next step.

(b)Forj=1,2,...,「N/2」,Bob performs the Bellbasis measurement on each pair inand obtains the corresponding measurement resultisConsequently,the corresponding pair inin TP’s hands is collapsed into one of the four Bell states.TP also performs the Bell-basis measurement on each pair inand obtains the corresponding measurement re-These「N/2」collapsed Bell states in TP’s hands are denoted by

(c)Forj=1,2,...,「N/2」,Alice and Bob cooperate to calculate

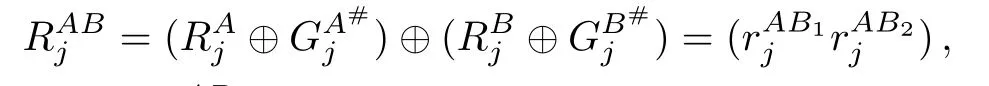
and sendto TP.Without loss of generality,we assume that Alice needs to send the result ofto Bob for calculating.Then,TP calculates

Afterward,TP publishesRABto Alice and Bob. IfRAB=0,Alice and Bob conclude thatX=Y;otherwise,they know thatX=Y.

Step 3The Second Round Comparison

(a)Charlie/TP prepares a sequence ofL′quantum states all in the state of|ϕ+＞to guarantee the security for the exchange ofandIf there is no eavesdropper,Charlie and TP drop out the sample particles,and implement the next step.

(b)Forj=1,2,...,「N/2」,Charlie performs the Bellbasis measurement on each pair inand obtains the corresponding measurement result isConsequently,the corresponding pair inin TP’s hands is collapsed into one of the four Bell states.TP also performs the Bell-basis measurement on each pair inand obtains the corresponding measurement result

(c)Forj=1,2,...,「N/2」,Alice,Bob and Charlie cooperate to calculate

and sendto TP.Without loss of generality,assume that Alice and Bob sendand the result ofto Charlie for calculatingrespectively.Then,TP calculates

In the meanwhile,forj=1,2,...,「N/2」,Alice,Bob,and Charlie cooperate to calculate

and sendto TP.Without loss of generality,assume that Alice and Bob send the result ofandto Charlie for calculating,respectively.Then,TP calculates

Finally,TP sendsRBCto Bob and Charlie.IfRBC=0,Bob and Charlie conclude thatY=Z;otherwise,they know thatY=Z.On the other hand,TP sendsRAC,to Alice and Charlie.IfRAC=0,Alice and Charlie conclude thatX=Z;otherwise,they know thatX=Z.Until now,the protocol is finished.

For clarity,the entanglement swapping process of Bell states among the four participants of the above three party QPC protocol is further shown in Fig.1.

Fig.1 The entanglement swapping of Bell states among the four participants.(a)Alice/Bob/Charlie/TP prepares quantum states in the state of|ϕ+＞A1A2/|ϕ+＞B1B2/|ϕ+＞C1C2/|ϕ+＞T1T2.(b)Alice and TP exchange the second particles A2and T2of the Bell states in their respective hands.(c)Particles T1and A2in TP’s hands become entangled together after Alice performs the Bell-basis measurement on particles A1and T2.(d)TP and Bob exchange particles A2and B2.(e)Particles T1and B2in TP’s hands become entangled together after Bob performs the Bell-basis measurement on particles B1and A2.(f)TP and Charlie exchange particles B2 and C2.(g)Particles T1and C2in TP’s hands become entangled together after Charlie performs the Bell-basis measurement on particles C1and B2.

4.2 Analysis

We analyze the above three-party QPC protocol from the aspects of correctness and security here.

(i)Correctness

There are three cases of correctness need to be discussed in total.

Case 1The Quality Comparison of Alice and Bob’s Secret Inputs

As for the quality comparison ofXandY,Alice and Bob need to calculateMoreover,TP needs to calculateAccording to Fig.1,the following evolution is satisfied:

Therefore,the quality comparison result ofXandYin the above three-party QPC protocol is correct.

Case 2The Quality Comparison of Bob and Charlie’s Secret Inputs

As for the quality comparison ofYandZ,Alice,Bob and Charlie need to calculateMoreover,TP needs to calculateAccording to Fig.1,the following evolution is satisfied:

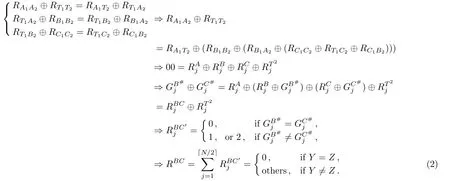
Therefore,the quality comparison result ofYandZin the above three-party QPC protocol is correct.

Case 3The Quality Comparison of Alice and Charlie’s Secret Inputs

As for the quality comparison ofXandZ,Alice,Bob and Charlie need to calculateMoreover,TP needs to calculateAccording to Fig.1,the following evolution is satisfied:

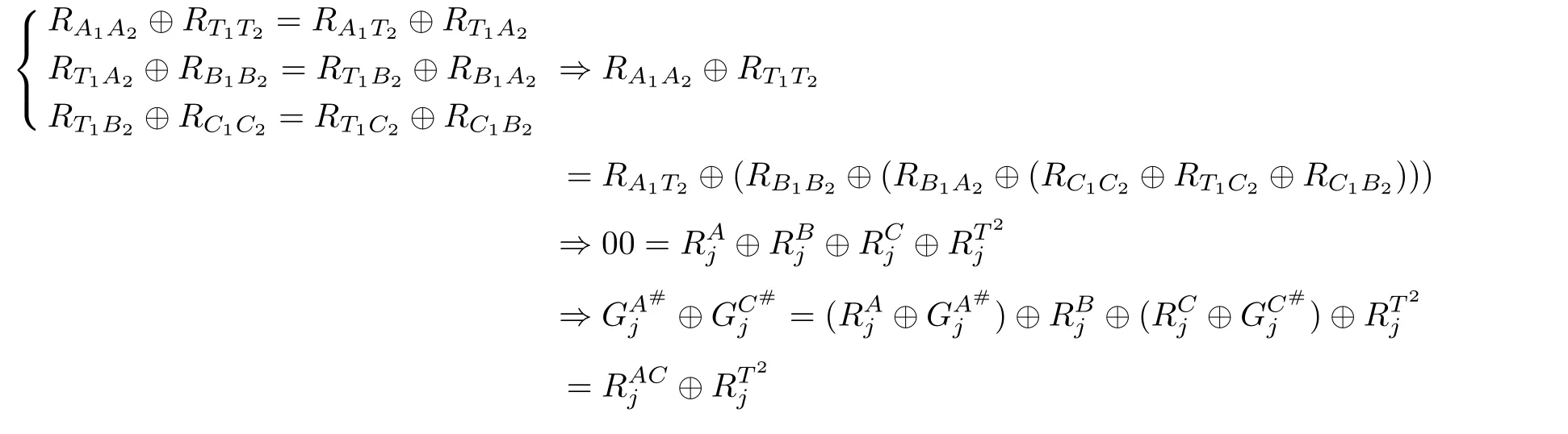
Therefore,the quality comparison result ofXandZin the above three-party QPC protocol is correct.

(ii)Security

As far as the security is concerned,all of the outside attack,the participant attack and the information leakage problem should be taken into account.

Case 1Outside Attack

We analyze the possibility for an outside eavesdropper to get information aboutX,Y,andZ.

In Step 1(c)/2(a)/3(a),TP and Alice/Bob/Charlie exchange two quantum state sequences in their respective hands.However,same to the LWC-QPC protocol,the entanglement correlation between two different particles of each Bell state is used to detect the eavesdropping behavior from an outside attacker.It has been widely accepted that several famous attacks,such as the intercept-resend attack,the measure-resend attack and the entangle-measure attacket al.,are invalid to this eavesdropping check method.[38−41]Moreover,except Steps 1(c),2(a)and 3(a),there is no chance for an eavesdropper to steal as no transmission for quantum states occurs.

In addition,in Steps 2(c)and 3(c),there are classical information transmissions.Suppose that the outside attacker is powerful enough to get all the transmitted classical information.In Step 2(c),the outside attacker obtains the result ofwhen Alice sends it out to Bob and the result ofwhen Bob sendsout to TP.However,as she has no knowledge about the onetime-pad keysandshe cannot deduce outrespectively.Similarly,in Step 3(c),the outside attacker can get other useful classical information includingand the result ofUntil now,the outside attacker can extractrespectively,since she has knownHowever,the one-way property of the hash function can guarantee that knowingis still helpless to deduceandrespectively.In this way,the outside attacker still has no access toand.On the other hand,the outside attacker cannot geteither since she does not knowRight now,it can be concluded that an outside eavesdropper cannot getX,YandZin the three-party QPC protocol.

Case 2Participant Attack

Gaoet al.[42]pointed out for the first time that the attack from dishonest participants,i.e.,the participant attack,is generally more powerful and should be paid more attention to.It has greatly aroused the interest of researchers in the cryptanalysis of quantum cryptography.There are two cases of participant attack in the three party QPC protocol.The first one is the attack from an insider user,while the second one is the attack from TP.

(a)Inside User’s Attack

Suppose that Alice is a powerful dishonest user who tries her best to get the other users’secret inputs with possible strong means.If Alice tries to intercept the transmitted particles from the TP-Bob channel,the Bob-TP channel,the TP-Charlie channel or the Charlie-TP channel,she will be caught as an outside attacker as analyzed in Case 1.Another way for Alice to get Bob and Charlie’s secret inputs is to utilize all the possible classical information in her hands.After the protocol is finished,all the possible classical information Alice has is,As a result,Alice can only deduce outfrom these classical information,but she still cannot knowsince she has no knowledge about.Moreover,the one-way property of the hash function can make Alice not aware ofGBjfrom.Therefore,Alice cannot getYandZ.

Suppose that Bob is a powerful dishonest user who tries his best to get the other users’secret inputs with possible strong means.If Bob tries to intercept the transmitted particles from the TP-Alice channel,the Alice-TP channel,the TP-Charlie channel or the Charlie-TP channel,he will be caught as an outside attacker as analyzed in Case 1.Another way for Bob to get Alice and Charlie’s secret inputs is to utilize all the possible classical information in his hands.After the protocol is finished,all the possible classical information Bob has isAs a result,Bob can only deduce outfrom these classical information,buthe still cannot knowsince he has no knowledge about Moreover,the one-way property of the hash function can make Bob not aware offrom.Therefore,Bob cannot getXandZ.

Suppose that Charlie is a powerful dishonest user who tries her best to get the other users’secret inputs with possible strong means.If Charlie tries to intercept the transmitted particles from the TP-Alice channel,the Alice-TP channel,the TP-Bob channel or the Bob-TP channel,she will be caught as an outside attacker as analyzed in Case 1.Another way for Charlie to get Alice and Bob’s secret inputs is to utilize all the possible classical information in her hands.After the protocol is finished,all the possible classical information Charlie has isAs a result,Charlie can deduce out bothfrom these classical information.However,according to the one-way property of the hash function,knowingstill helpless for Charlie to deducerespectively.Therefore,Charlie cannot getXandY.

(b)TP’s Attack

TP may try to get Alice,Bob and Charlie’s secret inputs with all the possible classical information in her hands.After the protocol is finished,all the possible classical information TP has isNote that TP need not launch the Bellbasis measurement attack to getandas she can get them from the public classical channels.As a result,TP can deduce out all offrom these classical information.However,according to the one-way property of the hash function,knowingandis still helpless for TP to deducerespectively.Therefore,TP cannot getX,Y,andZaccurately.

To sum up,in the three-party QPC protocol,TP can know the comparison result of each two users’secret inputs but cannot know the genuine value of each input.Each user cannot know the genuine values of the other two users’secret inputs.

Case 3The Information Leakage Problem

According to formulas(1)–(3),the relations betweenthe relations between′andand the relations betweenand,can also be depicted as Table 3,respectively.As analyzed in Subsec.3.2,the usage of one-way hash function can automatically avoid the information leakage problem pointed out in Subsec.3.1.

It can be concluded now that the three-party QPC protocol is highly secure.

5 MQPC Protocol Based on Entanglement Swapping of Bell Entangled States

There areKusers,P1,P2,...,PK,wherePihas a secret integerXi,i=1,2,...,K.The binary representationHere,∈{0,1},j=0,1,...,L−1.They want to know whether each two differentXiare equal or not with the help of a semi-honest TP.

They achieve the equality comparison of each two differentXiby implementing the following steps.Same to the above three-party QPC protocol,each transmission of quantum state sequence here is checked with the entanglement correlation between two different particles of a sample Bell stateFor simplicity,we omit the description of eavesdropping check processes in the following.

Step 1Preparation

(a)Similar to the QPC protocols of Refs.[4–5],Kusers,P1,P2,...,PK,share a secret one-way hash functionHin advance.The hash value ofXiisH(Xi)=vides her binary representation ofXi#into「N/2」groupswhere each group contains two binary bits.IfNmod 2=1,one 0 should be added to

(b)Pi/TP prepares「N/2」quantum states all in the state ofAfterward,Pi/TP picks out the first particle from each state to form an ordered sequenceThe remaining second particle from each state automatically forms the other ordered sequence

(c)P1and TP exchange

(d)Forj=1,2,...,「N/2」,P1performs the Bellbasis measurement on each pair inand obtains the corresponding measurement resultisConsequently,the corresponding pair inin TP’s hands is collapsed into one of the four Bell states.These「N/2」collapsed Bell states in TP’s hands are denoted by

Step kThe k−1thRound Comparison(k=2,3,4,...,K)

(a)Pkand TP exchange

(b)Forj=1,2,...,「N/2」,Pkperforms the Bell-basis measurement on each pair inand obtains the corresponding measurement resultIfMPk

jisquently,the corresponding pair inin TP’s hands is collapsed into one of the four Bell states.TP also performs the Bell-basis measurement on each pair inand obtains the corresponding measurement resultthen

(c)Forj=1,2,...,「N/2」,kusers cooperate to calculate

and sendto TP.Here,m=1,2,...,k−1.Without loss of generality,assume thatPi(i=1,2,...,m−1,m+1,...,k−2,k−1)andPmsendand the resultfor calculatingrespectively.

Then,TP calculates

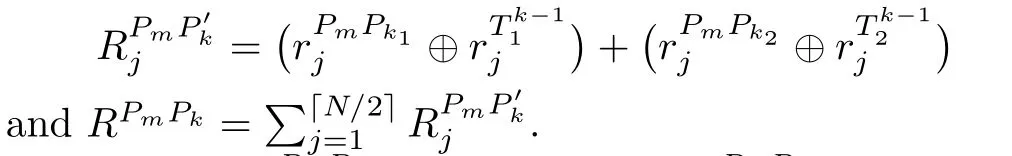
TP sendsRPmPktoPmandPk.IfRPmPk=0,Pmand

Pkconclude thatXm=Xk;otherwise,they know thatXm=Xk.

CorrectnessWe continue to demonstrate the output correctness.As for the quality comparison ofXmandXk(m=1,2,...,k−1 andk=2,3,4,...,K),kusers need to calculateMoreover,TP needs to calculate

andAccording to the entanglement swapping processes of the multi-party QPC protocol,we can obtain

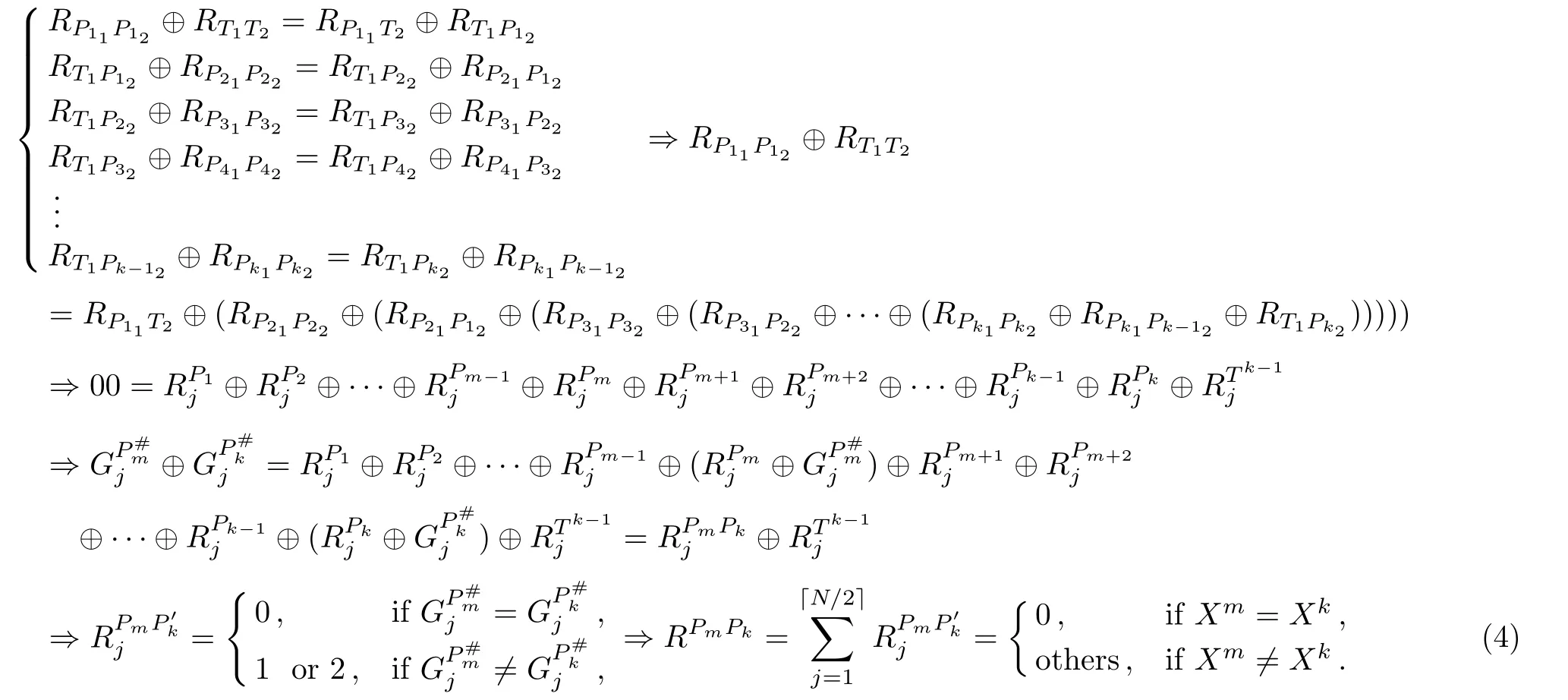
Therefore,the quality comparison result ofXmandXkin the aboveK-party QPC protocol is correct.

SecurityAs far as the security of the MQPC protocol is concerned,we can analyze it in a way similar to that of the three-party QPC protocol.It is easy to find out that the MQPC protocol is also immune to all of the outside attack,the participant attack and the information leakage problem.

Comparison with Previous QPC ProtocolsThe comparison of our MQPC protocol with some previous representative QPC protocols,such as Yanget al.’s protocol,[4]Chenet al.’s protocol,[6]Tsenget al.’s protocol,[7]Liuet al.’s protocol,[8]Yanget al.’s protocol[17]and Changet al.’s protocol,[35]is described in Table 4.According to Table 4,it is easy to know that each of the protocols in Refs.[4,6–8,17,35]has advantages and disadvantages more or less.For example,our protocol adopts Bell state as quantum resource.As for quantum state used,our protocol takes advantage over the protocols of Refs.[6,35]but is defeated by the protocol of Ref.[17],since the preparation of Bell state is easier than that of GHZ state and is more difficult than that of single photon product state.However,it can be concluded that our protocol exceeds the protocols of Refs.[4,6–8,17]in number of times of protocol execution when they are used to achieve the equality comparison amongKusers,because in our protocol,arbitrary pair’s comparison of equality amongKusers can be accomplished within one execution.

It should be further emphasized that different quantum methods have been used to achieve the equality comparison in present MQPC protocols[35−37]and our MQPC protocol.Concretely speaking,Changet al.’s protocol[35]uses the entanglement correlation between two different particles of onen-particle GHZ class state;both Liuet al.’s protocol[36]and Wanget al.’s protocol[37]use quantum fourier transform.However,our protocol uses quantum entanglement swapping.

6 Conclusion

In this paper,we first point out the information leakage problem toward TP in the LLCLL-improved-QPC protocol,and then mend this loophole by utilizing the one way hash function to encrypt the two users’secret inputs.Afterward,the three-party QPC protocol also based on entanglement swapping of Bell entangled state is constructed.Its output correctness and its security against the outside attack,the inside participant attack and the information leakage problem are validated in detail.Finally,the MQPC protocol also based on entanglement swapping of Bell entangled state is designed,where arbitrary pair’s comparison of equality amongKusers can be accomplished within one execution.

Appendix

Table 1 The relations among different parameters when =00.

Table 1 The relations among different parameters when =00.

|ϕ+＞ |ϕ+＞ 00 00 00/01/10/11 |ϕ+＞ 00 0/1/1/2|ϕ+＞ |ϕ−＞ 00 01 01/00/11/10 |ϕ−＞ 01 0/1/1/2|ϕ+＞ |ψ+＞ 00 10 10/11/00/01 |ψ+＞ 10 0/1/1/2|ϕ+＞ |ψ−＞ 00 11 11/10/01/00 |ψ−＞ 11 0/1/1/2|ϕ−＞ |ϕ−＞ 01 01 00/01/10/11 |ϕ+＞ 00 0/1/1/2|ϕ−＞ |ϕ+＞ 01 00 01/00/11/10 |ϕ−＞ 01 0/1/1/2 00 00/01/10/11 |ϕ−＞ |ψ−＞ 01 11 10/11/00/01 |ψ+＞ 10 0/1/1/2|ϕ−＞ |ψ+＞ 01 10 11/10/01/00 |ψ−＞ 11 0/1/1/2|ψ+＞ |ψ+＞ 10 10 00/01/10/11 |ϕ+＞ 00 0/1/1/2|ψ+＞ |ψ−＞ 10 11 01/00/11/10 |ϕ−＞ 01 0/1/1/2|ψ+＞ |ϕ+＞ 10 00 10/11/00/01 |ψ+＞ 10 0/1/1/2|ψ+＞ |ϕ−＞ 10 01 11/10/01/00 |ψ−＞ 11 0/1/1/2|ψ−＞ |ϕ+＞ 11 00 11/10/01/00 |ψ−＞ 11 0/1/1/2|ψ−＞ |ψ+＞ 11 10 01/00/11/10 |ϕ−＞ 01 0/1/1/2|ψ−＞ |ϕ−＞ 11 01 10/11/00/01 |ψ+＞ 10 0/1/1/2|ψ−＞ |ψ−＞ 11 11 00/01/10/11 |ϕ+＞ 00 0/1/1/2

Table 2 The relations between

Table 2 The relations between

0 00/01/10/11 00/01/10/11 1 00/01/10/11 01/00/11/10 10/11/00/01 2 00/01/10/11 11/10/01/00

Table 3 The relations between and

Table 3 The relations between and

0 00/01/10/11 00/01/10/11 1 00/01/10/11 01/00/11/10 10/11/00/01 2 00/01/10/11 11/10/01/00

Table 4 The comparison of our MQPC protocol with previous QPC protocols.

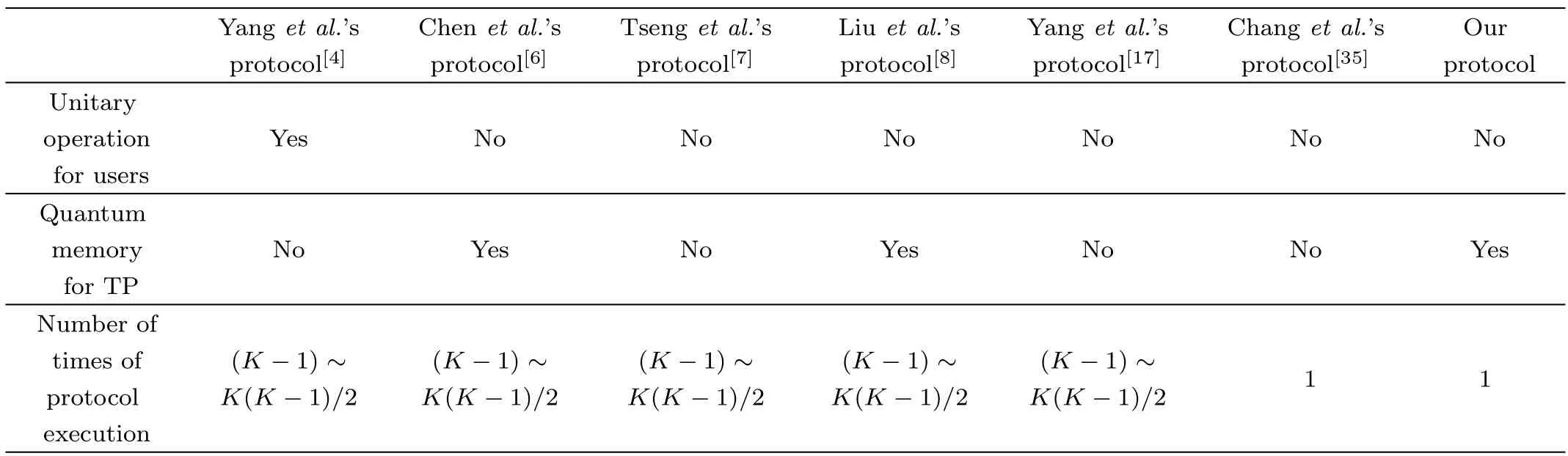
Table 4 (continued)

Acknowledgments

The author would like to thank the anonymous reviewer for his valuable suggestion that helps enhancing the quality of this paper.

[1]A.C.Yao,InProceedings of the 23rd Annual IEEE Symposium on Foundations of Computer Science,IEEE Computer Society,Washington(1982)160.

[2]F.Boudot,B.Schoenmakers,and J.Traore,Discret Appl.Math.111(2001)23.

[3]H.K.Lo,Phys.Rev.A 56(1997)1154.

[4]Y.G.Yang and Q.Y.Wen,J.Phys.A:Math.Theor.42(2009)055305;Y.G.Yang and Q.Y.Wen,J.Phys.A:Math.Theor.43(2010)209801.

[5]Y.G.Yang,J.W.Tian,Y.Hong,and H.Zhang,Phys.Scr.80(2009)065002;Y.G.Yang,W.F.Cao,and Q.Y.Wen,Phys.Scr.80(2009)065002.

[6]X.B.Chen,G.Xu,X.X.Niu,Q.Y.Wen,and Y.X.Yang,Opt.Commun.283(2010)1561.

[7]H.Y.Tseng,J.Lin,and T.Hwang,Quantum Inf.Process.11(2012)373.

[8]W.Liu,Y.B.Wang,and W.Cui,Commun.Theor.Phys.57(2012)583.

[9]W.J.Liu,C.Liu,H.W.Chen,Z.Q.Li,and Z.H.Liu,Commun.Theor.Phys.62(2014)210.

[10]J.Lin,H.Y.Tseng,and T.Hwang,Opt.Commun.284(2011)2412.

[11]C.Wang,G.Xu,and Y.X.Yang,Int.J.Quantum Inf.11(2013)1350039.

[12]Y.G.Yang,J.Xia,X.Jia,and H.Zhang,Quantum Inf.Process.12(2013)877.

[13]W.W.Zhang and K.J.Zhang,Quantum Inf.Process.12(2013)1981.

[14]W.Liu,Y.B.Wang,and Z.T.Jiang,Opt.Commun.284(2011)3160.

[15]Y.B.Li,Q.Y.Wen,F.Gao,H.Y.Jia,and Y.Sun,Eur.Phys.J.D 66(2012)110.

[16]W.Liu and Y.B.Wang,Int.J.Theor.Phys.51(2012)3596.

[17]Y.G.Yang,J.Xia,X.Jia,L.Shi,and H.Zhang,Int.J.Quantum Inf.10(2012)1250065.

[18]W.Liu,Y.B.Wang,and Z.T.Jiang,Int.J.Theor.Phys.51(2012)69.

[19]W.Liu,Y.B.Wang,Z.T.Jiang,Y.Z.Cao,and W.Cui,Int.J.Theor.Phys.51(2012)1953.

[20]H.Y.Jia,Q.Y.Wen,Y.B.Li,and F.Gao,Int.J.Theor.Phys.51(2012)1187.

[21]G.A.Xu,X.B.Chen,Z.H.Wei,M.J.Li,and Y.X.Yang,Int.J.Quantum Inf.10(2012)1250045.

[22]S.Lin,C.D.Guo,and X.F.Liu,Int.J.Theor.Phys.52(2013)4185.

[23]Z.W.Sun and D.Y.Long,Int.J.Theor.Phys.52(2013)212.

[24]W.Zi,F.Z.Guo,Y.Luo,S.H.Cao,and Q.Y.Wen,Int.J.Theor.Phys.52(2013)3212.

[25]B.Liu,F.Gao,H.Y.Jia,W.Huang,W.W.Zhang,and Q.Y.Wen,Quantum Inf.Process.12(2013)887.

[26]J.Lin,C.W.Yang,and T.Hwang,Quantum Inf.Process.13(2014)239.

[27]Y.T.Chen and T.Hwang,Int.J.Theor.Phys.53(2014)837.

[28]J.Li,H.F.Zhou,L.Jia,and T.T.Zhang,Int.J.Theor.Phys.53(2014)2167.

[29]Y.Li,Y.Ma,S.Xu,W.Huang,and Y.Zhang,Int.J.Theor.Phys.53(2014)3191.

[30]W.J.Liu,C.Liu,H.W.Chen,Z.H.Liu,M.X.Yuan,and J.S.Lu,Int.J.Quantum Inf.12(2014)1450001.

[31]W.J.Liu,C.Liu,H.B.Wang,J.F.Liu,F.Wang,and X.M.Yuan,Int.J.Theor.Phys.53(2014)1804.

[32]W.W.Zhang,D.Li,and Y.B.Li,Int.J.Theor.Phys.53(2014)1723.

[33]Z.W.Sun,J.P.Yu,P.Wang,L.L.Xu,and C.H.Wu,Quantum Inf.Process.14(2015)2125.

[34]G.P.He,Quantum Inf.Process.14(2015)2301.

[35]Y.J.Chang,C.W.Tsai,and T.Hwang,Quantum Inf.Process.12(2013)1077.

[36]W.Liu,Y.B.Wang,and X.M.Wang,Int.J.Theor.Phys.53(2014)1085.

[37]Q.L.Wang,H.X.Sun,and W.Huang,Quantum Inf.Process.13(2014)2375.

[38]G.F.Shi,X.Q.Xi,X.L.Tian,and R.H.Yue,Opt.Commun.282(2009)2460.

[39]G.F.Shi,Opt.Commun.283(2010)5275.

[40]G.Gao,Opt.Commun.283(2010)2288.

[41]T.Y.Ye and L.Z.Jiang,Chin.Phys.Lett.30(2013)040305.

[42]F.Gao,S.J.Qin,Q.Y.Wen,and F.C.Zhu,Quantum Inf.Comput.7(2007)329.