Fisher Information and Complexity Measure of Generalized Morse Potential Model

C.A.Onateand J.O.A.Idiodi

Physics Department,University of Benin,Nigeria

1 Introduction

In classical physics,the positions and momenta of every particle can be determined without any fundamental limitations.Thus,the uncertainty of position and momentum are caused by lack of precision of our measuring instruments.[1]It is noted that the state of a single nonrelativistic quantum particle can be described by a wave functionψ(r).The square of the modulus of this wave functionρ(r)=|ψ(r)|2determines the probability distribution of the position of the particle.Since the probability to find the particle anywhere must be equal to 1,the functionψ(r)must be normalized to unity.According to the density functional theory initiated by Hohenberg and Kohn,[2]the one particle position and momentum probability densities are the basic elements for describing the physical and chemical properties of some molecular systems.The quantum information theory plays an important role in the measurement of uncertainty and other quantum parameters of the system.[3]The basic measures of the quantum information are the Shannon entropy[4]and Fisher information.[5]The Shannon information entropy is the logarithmic function of the density which is the starting point of the methods of maximum entropy[6−8]and a global measure of the spreading of the density.The applications of Shannon entropy are found in many fields of studies e.g.biology,medicine,genetics,linguistics,economics,engineering,computer science,geophysics,chemistry,and physics.On the other hand,the Fisher information introduced in theory of statistical estimation by Fisher is the main theoretic tool of the extreme physical information principle that allows one to derive various fundamental equations of physics[9−12]and some conservation laws.In this paper,we deduce the information content stored in a system and the measure of the concentration of a quantum system(or disequilibrium).The Cramer–Rao uncertainty product(complexity measure “C”)has been obtained using the information content stored and disequilibrium system.

2 Calculation of Wave Function

The Schrdinger equation with the position dependent mass for any arbitrary potential is given as

whereEnℓis the energy spectrum andV(r)is the interacting potential,in this case,generalized morse potential.This potential takes the form[13−14]

whereDeis the dissociation energy andreis the equilibrium bond length.The centrifugal term~2ℓ(ℓ+1)/2µr2is replaced by[15−16]

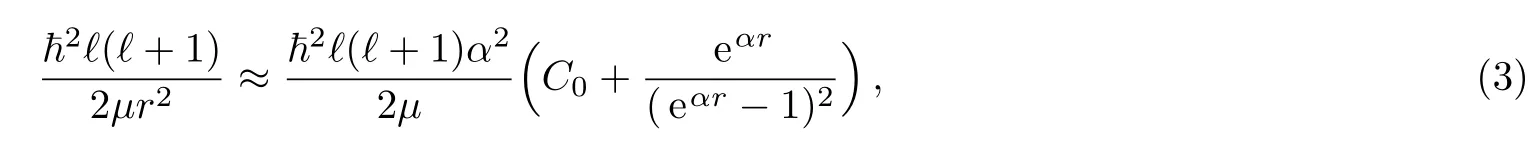
whereC0=1/12.With Eqs.(2)and(3),Eq.(1)becomes

In this paper,we use formula method to obtain the wave function.definings=e−αrandb=eαre−1,Eq.(4)turns to be[17]

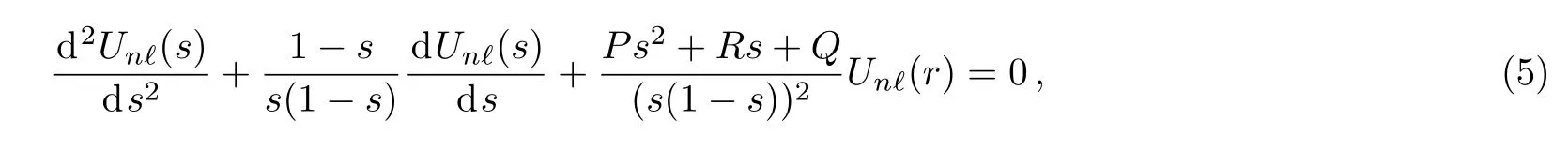
where

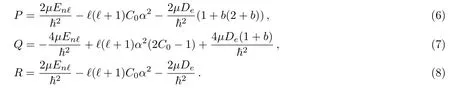
The wave function is thus given as[17]

Comparing Eq.(5)with equation of the form[17]

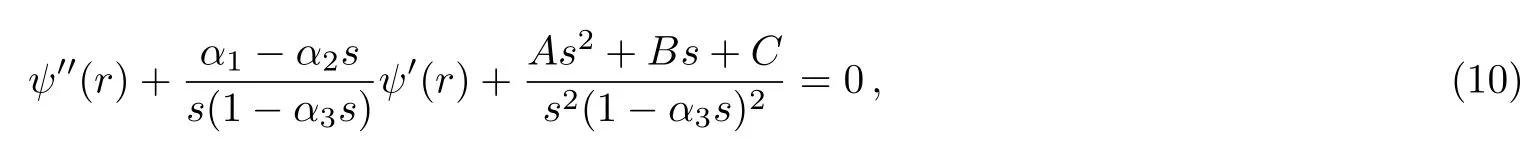
we deduce the following

In order to obtain the normalization constant,we used the normalization condition,

Using Jacobi hypergeometric function

Thus,the normalization constant is obtained as

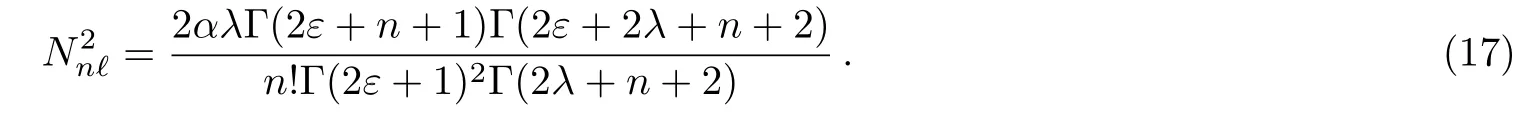
3 Shannon Information Entropy,Information Energy and Uncertainty Measure for Generalized Morse Potential

3.1 Shannon Information Entropy

The Shannon information entropy for position space and momentum space are given as[18−19]

respectively.In order to obtain the solutions of Eqs.(18)and(19),we normalized the wave function of Eq.(9)to unity and then obtained the probability distribution as

Substituting Eq.(20)into Eq.(18),we have

Using the relation(16)and the one below

The Shannon entropy in the position space is obtained as

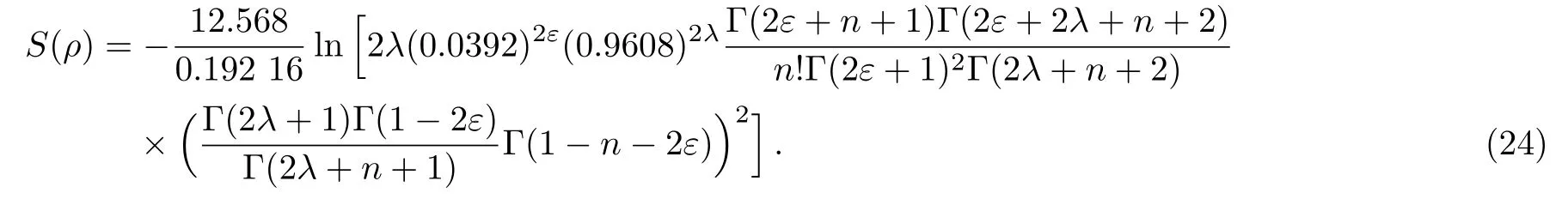
To obtain the momentum space of the Shannon entropy for the generalized morse potential,we use Nikiforov–Uvarov method and recast the wave function of Eq.(20)as

wherea=2λandb+1=2ε.Substituting Eq.(25)into Eq.(19),we have

where

Using Eq.(23)and the standard integral

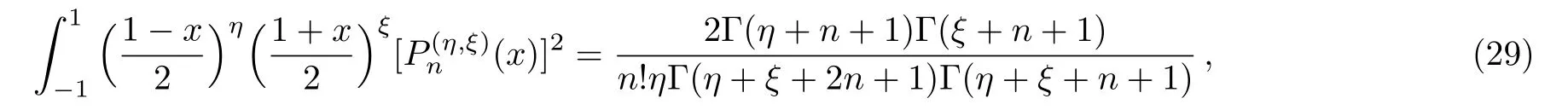
we obtain the Shannon entropy for the momentum space as

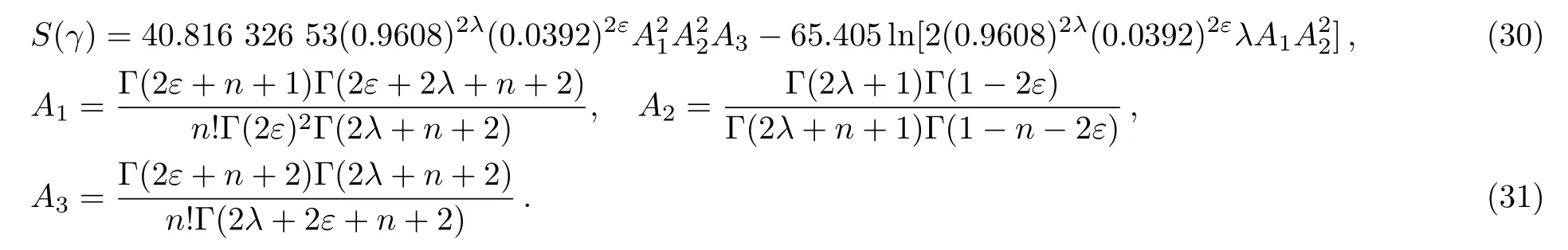
It is now convenient to calculate the information content stored in the system which is the total Shannon information entropy of a system.The information content storedSTof any system is given as

Substitute Eqs.(24)and(30)into Eq.(32),the information content stored is obtained as

3.2 Information Energy of Generalized Morse Potential

The information energy for the position space is given as

Substituting Eq.(20)into Eq.(34)to have

The momentum space of the information energy is given as

Substituting Eq.(25)into Eq.(38)we have

Using standard integral of the form

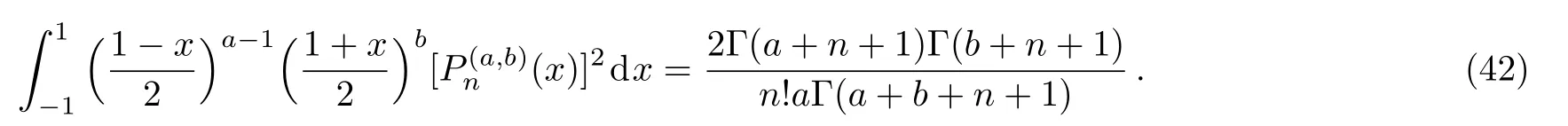
Equation(41)becomes

Thus,the disequilibrium of the system or the measure of the concentration of a quantum system is calculated using

Substituting the values ofE(ρ)andE(γ),into Eq.(44),we obtainETas

3.3 Complexity Measure C

The complexity measure of a quantum system is the product of the total Shannon information entropy and the concentration of the information energy.This is equivalent to the Cramer–Rao uncertainty product.It is given as

Now,substituting the values ofSTandETinto Eq.(48),we obtain the Cramer–Rao uncertainty product as

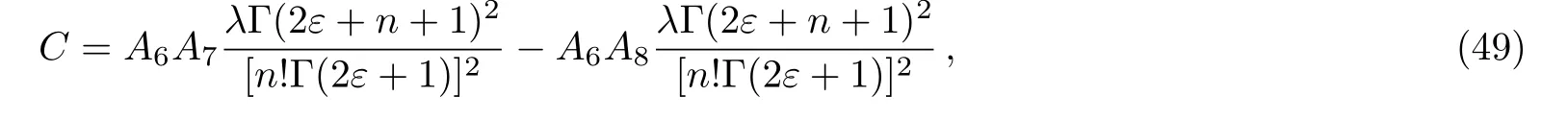
where

4 Conclusion

In this paper,the Shannon entropy and information energy of quantum system have been investigated for the spreading of the position and momentum spaces for a known generalized morse potential model used in molecular and atomic physics.These describe the chemical and physical properties of the system.We have equally obtained the information content stored and the concentra-tion of the quantum system.With these two obtained quantities,the complexity measure which is equivalent to Cramer–Rao uncertainty product is calculated.Numerically,the information content increases as the principal quantum number increases.The concentration of the quantum system increases as the principal quantum number increases.Similarly,the complexity measure increases as the principal quantum number increases.Table 1 above shows the numerical computation of the Information content,concentration of the quantum system and complexity measures.

Table 1 Information content stored ST,disequilibrium ET,and complexity measure C.

Acknowledgments

We are grateful to the kind referee and editor for their patience and positive suggestions for the success of this research work.

[1]E.Romera,P.Sanchez-Moreno,and J S.Dehesa,Chem.Phys.Lett.414(2005)468.

[2]P.Hohenberg and W.Kohn,Phys.Rev.136(1964)8864.

[3]B.J.Falaye,F.A.Serrano,and H.S.Dong,Phys.Lett.A 380(2016)267.

[4]C.E.Shannon and W.Weaver,The Mathematical Theory of Communication,University Press,Cambridge(2004).

[5]B.R.Freiden,Science from Fisher Information,Cambridge University Press,Cambridge(2004).

[6]C.E.Shannnon,Bell Syst.Tech.J.27(1948)623.

[7]J.S.Dehesa and S.Lopez-Rosa,and B.Olmos,J.Math.Phys.47(2006)052104.

[8]R.A.Fisher,Proc.Cambridge Philos.Soc.22(1925)700.

[9]R.A.Fisher,Statistical Methods and Scientific Inferences,2nd.,Oliver and Boyd,London(1959).

[10]B.R.Frieden,Physics from Fisher Information,Cambridge University Press,Cambridge,USA(1999).

[11]B.R.Frieden and B.H.So ff er,Phys.Rev.E 52(1995)2274.

[12]M.Reginatto,Phys.Rev.A 58(1998)1775.

[13]Z.H.Deng and Y.P.Fan,J.Shandong University,Shandong 7(1957)162.

[14]S.H.Dong and X.Y.Gu,J.Phys.Conf.Series 96(2008)1.

[15]C.S.Jia and T.Chen,and G.Cui,Phys.Lett.A 373(2009)21.

[16]L.H.Zhang,X.P.Li,and C.S.Jia,Int.J.Quan.Chem.111(2011)1870.

[17]B.J.Falaye,S.M.Ikhdar,and M.Hamzavi,Few-Body Syts.56(2015)63.

[18]J.S.Dehesa,W.V.Assche,and R.J.Yanez,Meth.Applic.Analysis 4(1997)91.

[19]W.A.Yahya,K.J.Oyewumi,and K.D.Sen,J.Math.Chem.(2016),doi.10.1007/S10910-016-0657.