Entropy,Fisher Information and Variance with Frost-Musulin Potenial

J.O.A.Idiodi and C.A.Onate

Physics Department,University of Benin,Benin,Nigeria

1 Introduction

There has been a great interest in studying information theoretic measures for different quantum systems because the information theory of quantum-mechanical systems are related to the modern quantum communication and density functional methods.[1−2]The quantum information plays a crucial role in the measurement of uncertainty and other quantum parameters of the system.[2]The information entropy is a superior measure of spreading and then of quantum uncertainity,a property of fundamental relevance for the adequate characterization of the position and momentum densities.[3−5]The entropies have been used for numerous practical purposes e.g.measure the squeezing of quantum fluctuation[6]and to reconstruct the charge and momentum densities of atomic and molecular systems[7−8]by means of maximum entropy procedures.The Fisher information is the basic variable of the principle of extreme physical information which has been used to obtain various fundamental equations of motion in physics.[9]It is equally being used to rederive classical thermodynamics without the usual concept of Boltzmann’s entropy.It is understood that the position-space Shannon entropyS(ρ)measures the uncertainity in the localization of a particle in space while the momentum-spacenthe Shannon entropy measures the uncertainity in predicting the momentum of the particle.[10]These entropies are closely related to fundamental and experimentally measurable quantities such as the kinetic energy and magnetic susceptibility,which make them useful in the study of the structure and dynamics of atomic and molecular systems.[8]Thus in this paper,we calculate both the position and momentum of the Shannon entropy and Renyi entropy,the Fisher information and Variance of a system and the observed behavior of these quantities with the quantum numbern.We compute the wave function in Sec.2.In Sec.3,we show the basic equation in this work.Section 4 presents the Shannon,Renyi entropies,Fisher information and variance.In the fi nal section,we give the conclusion.

2 Wave Function of Radial Schrdinger Equation with Frost-Musulin Potential

Given the Radial Schrdinger Equation as[11]

and the Frost–Musulin potential as

where

Substitute Eqs.(2)and(3)into Eq.(1)and by defining a variable of the formy=e−δr,we have a differential equation of the form

where

The wave function is obtained as

where

3 Basic Equations

In this section,we write some equations that are useful in this work.The Shannon information entropyS(ρ)andS(γ)of the electron densityρ(r)in the coordinate space for position and momentum space respectively are defined as[12−14]

whereγ(p)denotes the momentum density.The Renyi position entropy is defined as[15−18]

It is a generalization of the Shannon entropy.The corresponding momentum space entropy is given as[14]

The Fisher information entropy of the radial probability distributionρ(r)function is calculated by using[19]

The position Variance is given as[19]

4 Frost-Musulim Potential with Shannon Entropy,Renyi Entropy,Fisher Information and Variance

To obtain the Shannon and Renyi entropies in the position space,we define the radial probability distribution functionρ(r)for this problem as the square of the radial wave function and obtain the following

where,

4.1 Shannon Entropy for the Frost-Musulin Potential

Entropy is a thermodynamic quantity representing the unavailability of a system’s thermal energy for conversion into mechanical work.It is often interpreted as the degree of disorder or randomness in the system.Shannon entropy is the expected value or average of the information contained in each message.It measures the information in a message as opposed to the portion of the message that is determined.Shannon entropy can determine the minimum channel capacity required to reliably transmit the source as encoded binary digit.

To obtain the position space for the Shannon entropy,we substitute Eq.(14)into Eq.(8)and have

where we have used the following for mathematical simplicity;

By using the identity in Appendix B and standard integral in Appendix A,we obtain the Shannon entropy in the position space as

whenn=1,

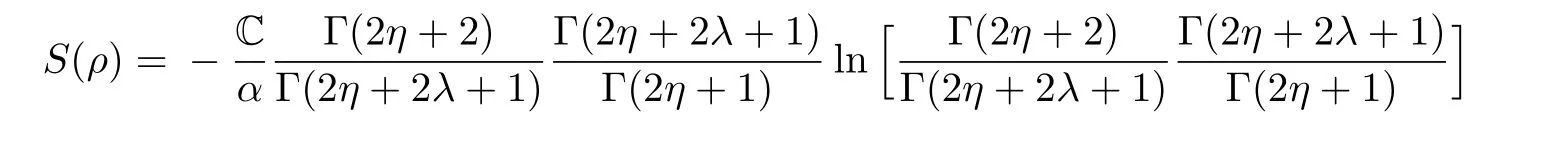
The momentum space of the Shannon entropy is obtained by substituting Eq.(15)into Eq.(9)to have

where=lnγ(p).Using the relation in Appendix B and integral in Appendix A,we obtain the Shannon entropy in the momentum space as

4.2 Renyi Entropy for the Frost-Musulin Potential

To obtain the position-space for the Renyi-entropy,we substitute Eq.(14)into Eq.(10)to have

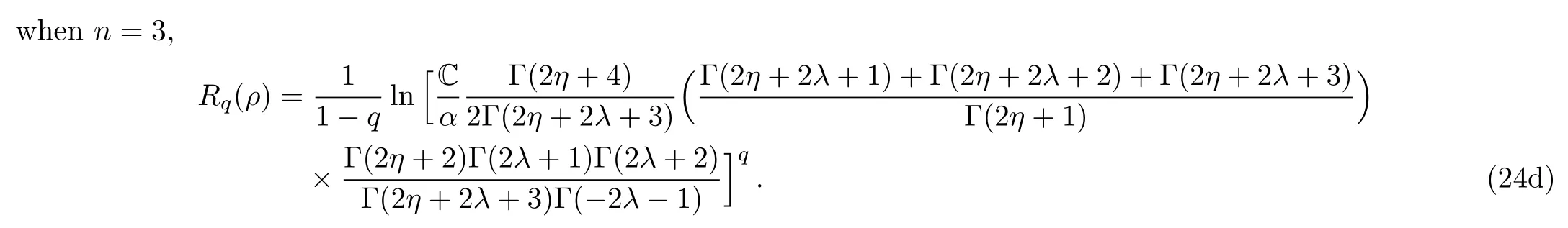
The Renyi entropy in the momentum space is obtained by substituting Eq.(15)into Eq.(11)to have

which gives

4.3 Fisher Information Entropy for the Frost-Musulin Potential

To obtain the Fisher information entropy,we substitute Eq.(14)into Eq.(13)and then solve it bit by bit as follows

where

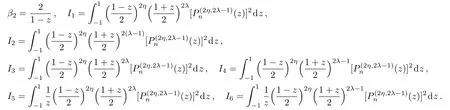
Thus,we obtain the Fisher information entropy as

4.4 Variance with Frost-Musulin Potential

Using Eq.(13),we obtain the following

Here,we obtain the information content in terms of the Shannon entropy and Renyi entropy.The information content in terms of Shannon entropy is given as

Equation(32)thus gives the uncertainty relation.The information content in terms of Renyi entropy is defined as

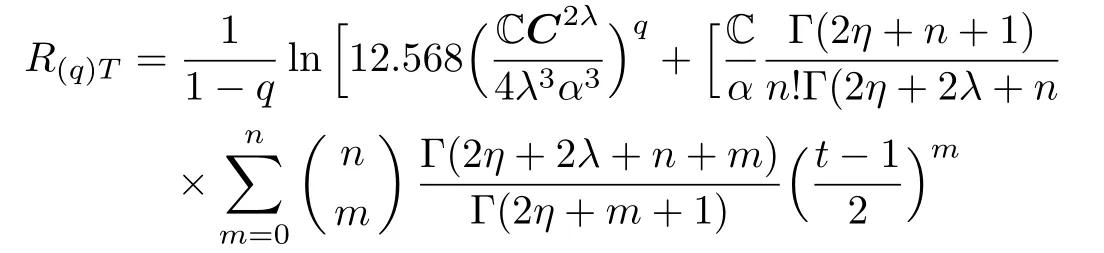
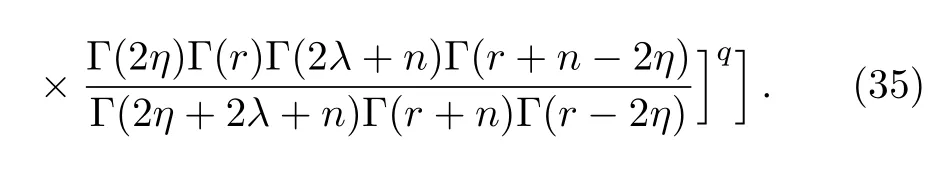
5 Conclusion

In this paper,we have calculated the position-space and momentum-space of the Shannon entropy and Renyi entropy,the Fisher information and the variance of the Frost-Musulin potential.The information-theoretic measures of the localization of the quantum-mechanical distribution density of the system are obtained in a closed and compact form.The Shannon entropy gives the average of information contained in each message in any quantum mechanical system.The Fisher information describes the concentration of the density around its nodes,providing a measure of the oscillatory character of the corresponding wave function.This describes the chemical and physical properties of the systems.The computed variance gives the spreading around the centroid.However,we have computed the Shannon entropy,the Renyi entropy,the Fisher information and variance for various values ofn.It is observed that the Shannon entropy,the Renyi entropy,the Fisher information and variance all decrease with increasing quantum numbernrespectively.

Appendix A

Appendix B

[1]E.Romera,P.Sanchez-Moreno,and J.S.Dehesa,Chem.Phys.Lett.414 (2005)468,doi: 10.1016/j.cplett.2005.08.032

[2]B.J.Falaye,F.A.Serrano,and S.H.Dong,Phys.Lett.A(2015),doi:org/10.1016/j.physleta.2015.09.029.

[3]P.Hohenberg and W.Kohn,Phys.Rev.A 136(1964)864,doi:10.1103/PhysRevA.136.B864.

[4]P.G.Parr and W.Yang,Theory of Atoms and Molecules,Oxford University Press,Oxford(1989).

[5]N.H.March,Electron Density Theory of Atoms and Molecules,Academic Press,New York(1992).

[6]A.Orlowski,Phys.Rev.A 56(1997)2545.

[7]A.Galindoand P.Pascual,QuantumMechanics,Springer,Berlin(1978).

[8]J.C.Angulo,J.Antolin,A.Zarzo,and J.C.Cuchi,Eur.Phys.J.D 7(1999)479.

[9]B.R.Frieden,Science from Fisher Information,Cambridge University Press,Cambridge(2004).

[10]J.S.Dehesa,A.Martinez-Finkelshtein,and J.Snchez-Ruiz,J.Comput.Appl.Math.133(2001)23,doi:Pll s0377-0427(00)00633-6.

[11]S.M.Ikhdair,M.Hamzavi,and B.I.Ita,Phys.Scr.85(2012)045009,doi:10.1088/0031-8949/85/04/045009

[12]K.D.Sen and J.Katriel;J.Chem.Phys.125(2006)074117,doi.org/10.1063/1.2263710.

[13]W.A.Yahya,K.J.Oyewumi,and K.D.Sen,J.Math.Chem.(2016),doi.10.1007/s10910-016-0657.

[14]J.S.Dehesa,R.J.Yanez,A.I.Aptekarev,and V.Buyarov,J.Math.Phys.39(1998)3050,doi:10.1063/1.2190-335

[15]E.Romera and A.Nagy,Phys.Lett.A 372(2008)6823,doi:10.1016/j.physleta.2008.10.027.

[16]S.Lopez-Rosa,J.C.Angulo,J.S.Dehesa,and R.J.Yanez,Phys.Lett.A.387(2008)2243.doi:10.1016/j.physa2007.12.005.

[17]F.de los Santos,C.Guglieri,and E.Romera,Physica E 42(2010)303,doi:10.1016/j.physe 2009.06.078.

[18]A.I.Aptekarev,J.S.Dehesa,and A.Martinez-Finkelshtein,J.Comput.Appl.Math.233(2010)1355,doi.org/10.1090/jams/853.

[19]B.J.Falaye,K.J.Oyewumi,S.M.Ikhdar,andM.Hamzavi, Phys. Scr. 89 (2014) 115204, doi:10.1088/0031.8949/89/1152204.

[20]J.S.Dehesa,A.Martinez-Finkelshtein,and V.N.Sorokin,Mol.Phys.34(2006)613.