On Recursion Operator of the q-KP Hierarchy∗

Ke-Lei Tian(田可雷), Xiao-Ming Zhu(朱晓鸣),and Jing-Song He(贺劲松)

1School of Mathematics,Hefei University of Technology,Hefei 230009,China

2Department of Mathematics,Ningbo University,Ningbo 315211,China

1 Introduction

Theq-deformed Kadomtsev–Petviashvili(q-KP)hierarchy[1−12]is an interesting subject of intensive study in the integrable systems,which can be defined formally by means of theq-derivative∂q[13−14]instead of the usual derivative∂with respect toxin the Kadomtsev–Petviashvili(KP)hierarchy.[15−16]Asq→1,∂qgoes to∂,thenq-KP reduces to KP hierarchy.So main motivation of the research of theq-KP hierarchy is to explore two aspects:integrable properties inherited from KP hierarchy,and the difference(or called “q-effect”)betweenq-KP and KP hierarchy.On the one side,it has been shown thatq-KP hierarchy inherits some integrable properties,such as bi-Hamiltonian structure,in finite conservation laws,τfunction,additional symmetries and symmetry constraint sub-hierarchy[2−3,5,7,9]from KP hierarchy.On the other side,the “q-effect” can be observed[9]intuitionally single q-soliton of theq-KP equation:qdeformation does not destroy the pro file of soliton,it is just similar to an “impulse” to soliton,which can be thought of a non-uniform translation[5]of dynamical variablestibetweenτqKPandτKP,i.e.,τqKP(ti)=τKP(ti→˜ti=ti+((1−q)i/i(1−qi))xi).This translationti→˜tiis also re-delivered in the Virasoro constraint of theq-KP hierarchy.[12]Because quantum calculus[14]is one kind of calculus in non-commutative plane,these results of theq-KP hierarchy just demonstrate the internal properties of the dynamical evolution of the noncommutative plane.H-calculus is another one of the calculus in non-commutative plane.What is more,theqdeformed,differential-difference systems[17−19]are corresponding to theq-calculus andh-calculus respectively.

Up to now,there are still two questions in the study of theq-KP hierarchy:(i)What is the distinct difference between the fl ow equations of theq-KP and KP hierarchy?(ii)Is there recursion operator for theq-KP hierarchy undern-reduction?The central work of this paper is to solve these questions starting from the Lax equations of theq-KP hierarchy.For the KP hierarchy,noncommutative KP hierarchy and Dispersionless KP Hierarchy,there are several methods to construct the recursion.[20−24]Here we use Strampp and Oevel’s method to get a general formula of the recursion operator.

The organization of this paper is as follows.After reviewing some basic results ofq-KP hierarchy,we give two general expressions of fl ow equations in Sec.2.In particular,a single componentq-KP family equation about the dynamical coordinateu1ofq-KP hierarchy is obtained,and then-reduction is also discussed in this section.The recursion operators for then-reducedq-KP hierarchy are given in Sec.3.Section 4 is devoted to conclusions and discussions.

At the end of this section,let us recall some useful facts of theq-calculus[14]in the following to make this paper be self-contained.Theq-derivative∂qis defined by

and theq-shift operator is

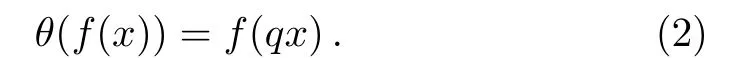
It is worth pointing out that theq-shift operatorθdoes not commute with∂q,indeed,the relation(∂qθk(f))=qkθk(∂qf),k∈Z holds.∂q(f(x))recovers the ordinary differentiation∂x(f(x))asqgoes to 1.Let∂−1qdenote the formal inverse of∂q.In general the followingq-deformed Leibnitz rule holds

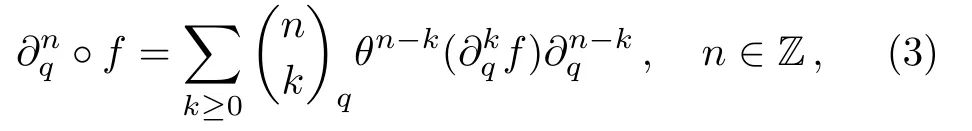
where theq-number and theq-binomial are defined by

For example,

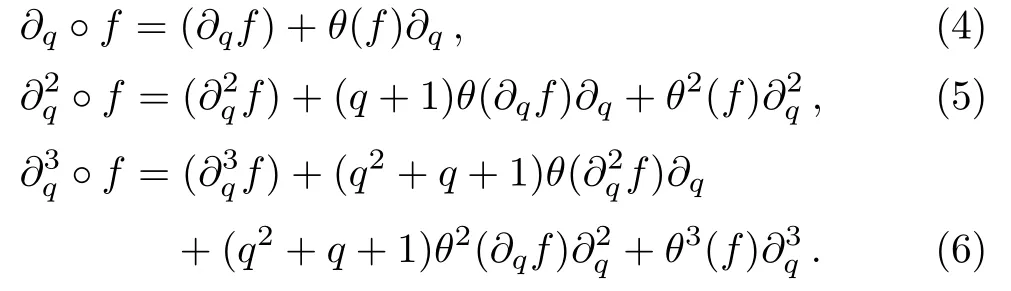
By comparing with Leibnitz rule for∂n◦f,the difference in Eq.(3)is due toq-binomial and the action ofq-shift operatorθ.This simple observation is crucial to find the difference between the fl ow equations of theq-KP and KP hierarchy.Moreover,for aq-pseudo-differential operator(q-PDO)of the form

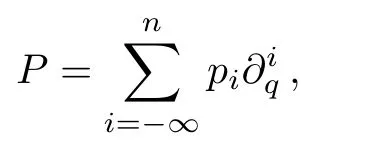
we separatePinto the differential part

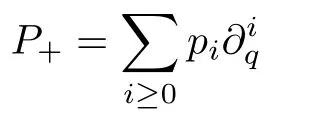
and the integral part

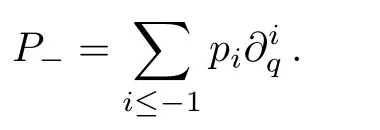
2 Flow Equations of theq-KP Hierarchy

Similar to the general way of describing the classical KP hierarchy,[15−16]we first give a brief introduction ofq-KP hierarchy based on Ref.[5].

LetLbe oneq-PDO given by

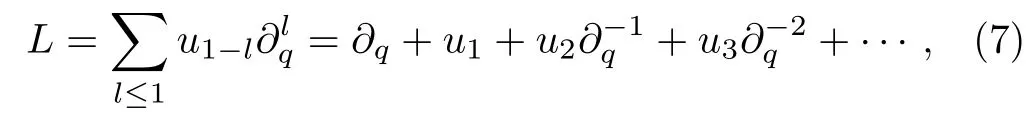
withu0= 1,the operator is called Lax operator ofq-KP hierarchy. There exist in finite number ofqpartial differential equations related to dynamical variables{ui(x,t1,t2,t3,...),i=1,2,3,...}and can be deduced from the generalized Lax equations,

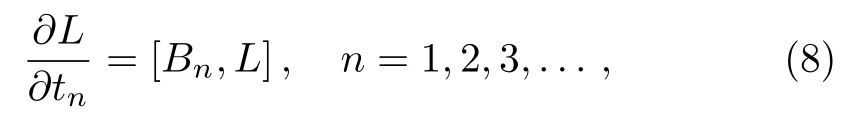
which are calledq-KP hierarchy.Here

We fix a natural numbernand define the sets of functionspj,j≤nandqj,j≤nas the coefficients in then-th power on∂qofL:

where

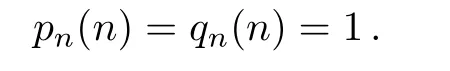
There is a one to one correspondence between(u1,u2,u3,...)and(pn−1(n),pn−2(n),pn−3(n),...),also(u1,u2,u3,...)and(qn−1(n),qn−2(n),qn−3(n),...).Moreover,we note that the functionsqj(n)(andpj(n))are uniquely determined as functions of{u1,u2,...,un−j−1,un−j}as

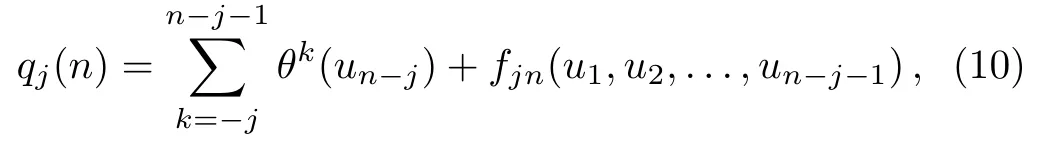
wherefjnare differential polynomials with∂qof{u1,u2,...,un−j−1,un−j}.For example,

By comparing withq−h(n)of the KP hierarchy,[20]it is easy to know that the distinct difference of Eq.(10)is due toq-binomial and the action ofq-shift operatorθ.

The differential part ofis

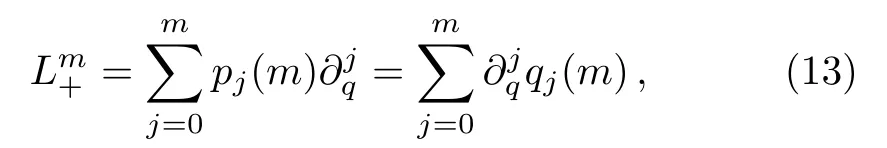
and the integral part is

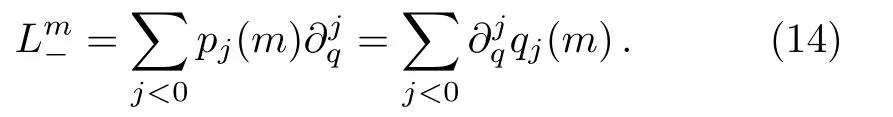
By a straightforward calculation,the relation betweenpj(n)andqj(n)is given as

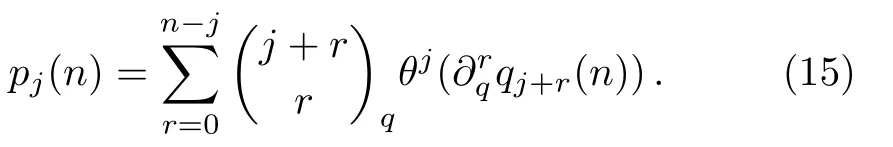
Theorem 1The fl ow equations of theq-KP hierarchy can be expressed as

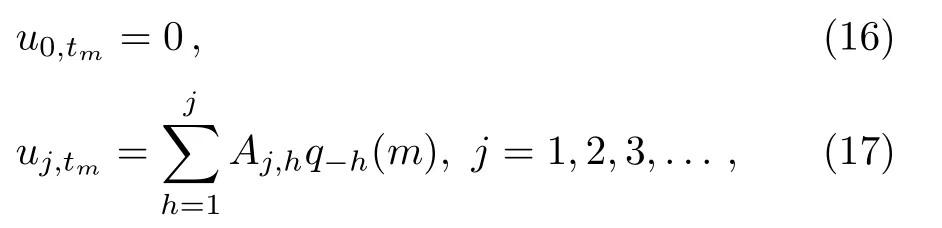
where the differential operator

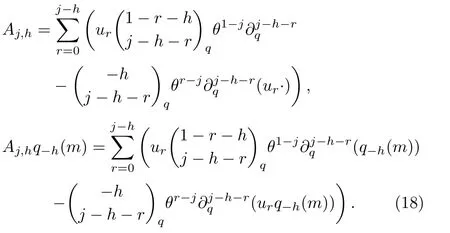
ProofThe first fl ow equationu0,tm=0 is obvious because of the factu0=1.

Note that

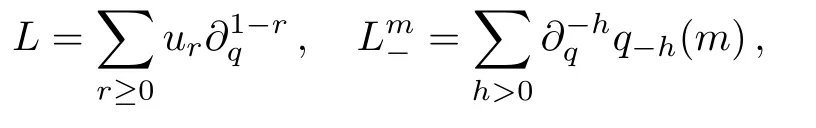
following the Lax equation of theq-KP hierarchy

we have

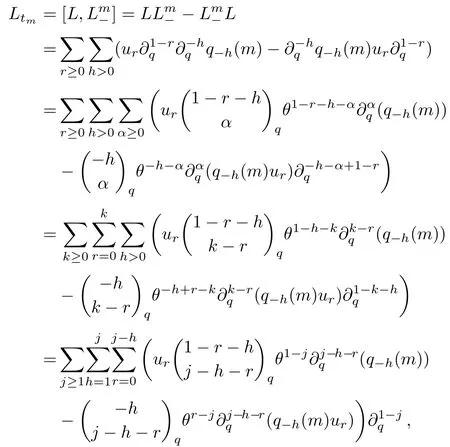
wherek=r+αandj=k+h.Combining the above equation with

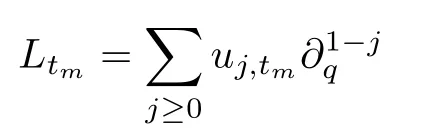
finishes the proof.

Remark 1We can see that the main difference between fl ow equations of the KP hierarchy andq-KP hierarchy is due toq-binomial and the action ofq-shift operatorθ,which is appeared inAj,handq−h(m).This distinct difference originates from the essential property of quantum calculus,i.e.q-deformed Leibnitz rule Eq.(3).

We write out several explicit forms of operatorsAj,has

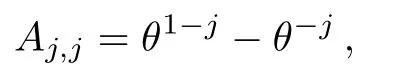
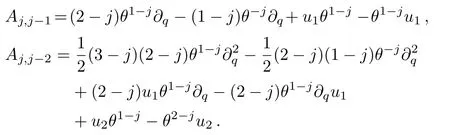
The first two fl ow equations of theq-KP hierarchy can be given by

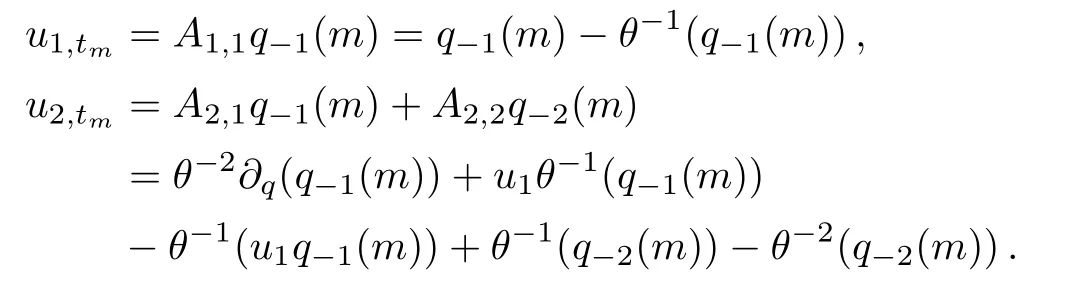
Letm=1,2 and usinguisubstitute forq−j(m),we will get the fl ow equations ofu1,u2ont1,t2respectively as

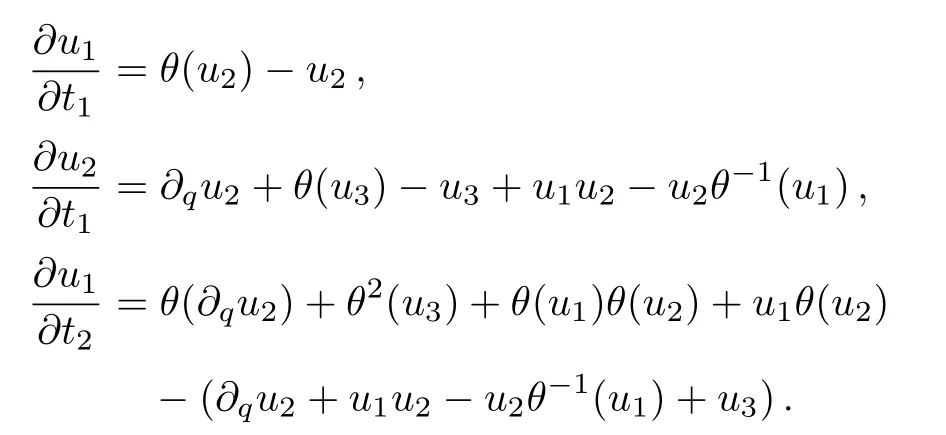
Solving these above equations we arrive at the following equation of a single componentq-KP family

Let us consider then-reducedq-KP hierarchy,letLbe a purely differential operator,i.e.Ln=Ln+.

Theorem 2The Lax equations ofn-reducedq-KP hierarchy can be written in the finite matrix form as

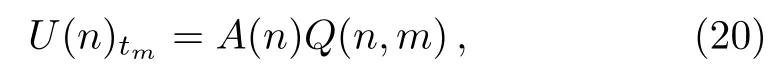
where

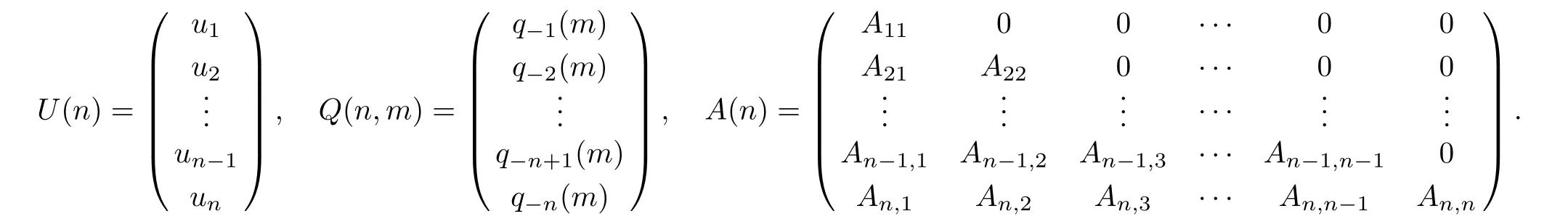
ProofFrom Eq.(10)andLn=,it is easy to knowqj(n)=0 forj<0.

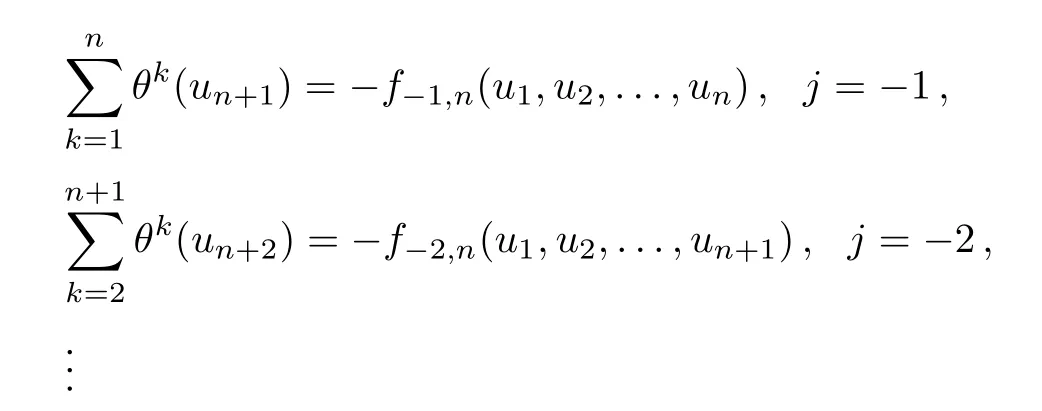
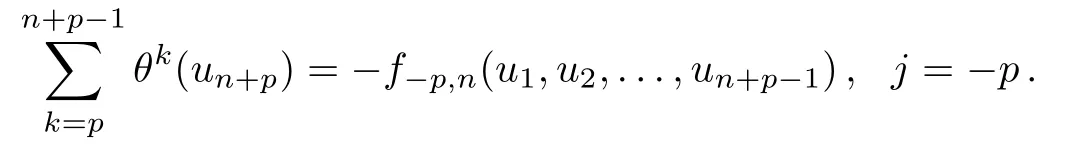
The above equations show that(un+1,un+2,...,un+p)depending only on(u1,u2,...,un). This means that in the case ofn-reduction,only the firstndynamical coordinates(u1,u2,...,un)are independent.Equation(10)tells us the coordinates(qn−1(n),qn−2(n),qn−3(n),...)become to be finite (q0(n),q1(n),q2(n),...,qn−1(n)),and (pn−1(n),pn−2(n),pn−3(n),...)are also finite as(p0(n),p1(n),p2(n),...,pn−1(n)). Then-reducedq-KP hierarchy defined by Eq.(19)is a closed time-evolution system of(u1,u2,...,un).Now we can write the Lax equations Eq.(19)of then-reducedq-KP hierarchy as

U(n)tm=A(n)Q(n,m).

The above two theorems are based on the coordinates{q−1(m),q−2(m),...,q−n(m)},we also can express the fl ow equations of theq-KP hierarchy by another family of coordinates{p−1(m),p−2(m),...,p−n(m)}.

Theorem 3The fl ow equations of theq-KP hierarchy can be expressed as

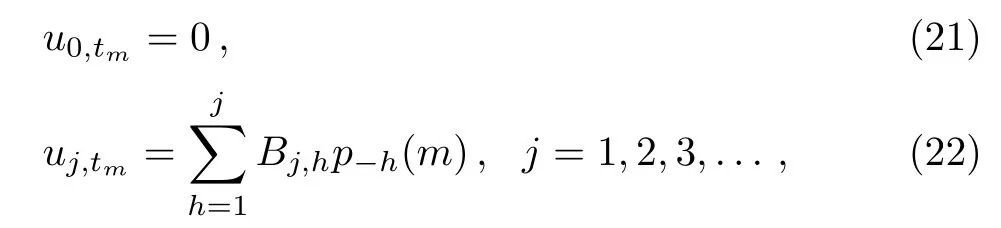
where the differential operator

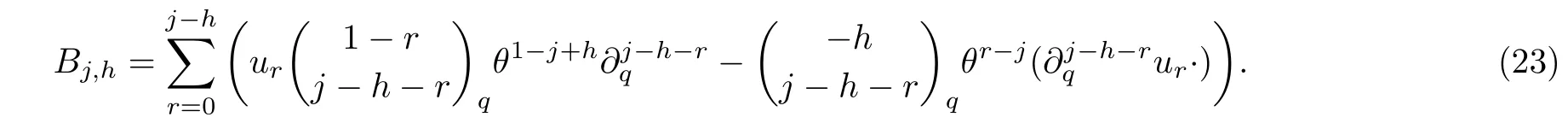
Theorem 4The Lax equations ofn-reducedq-KP hierarchy can be written in the finite matrix form as

where

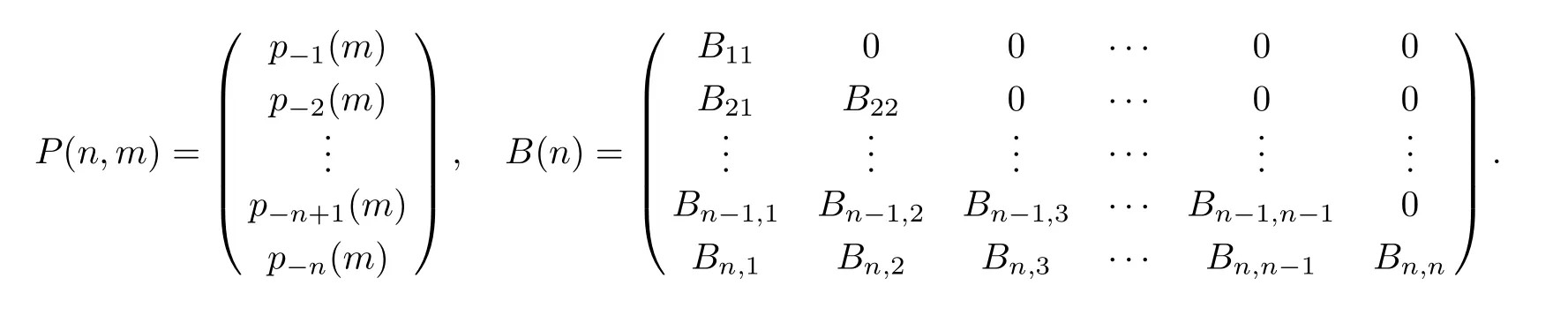
3 Recursion Operator ofn-Reducedq-KP Hierarchy

In this section,we shall give a recursion formula relatingP(n,n+m)andP(n,m),and a recursion operator mapping the lower order fl ow equations to higher order fl ow equations ofn-reducedq-KP hierarchy.To this end,we first state two useful Lemmas.

Lemma 1

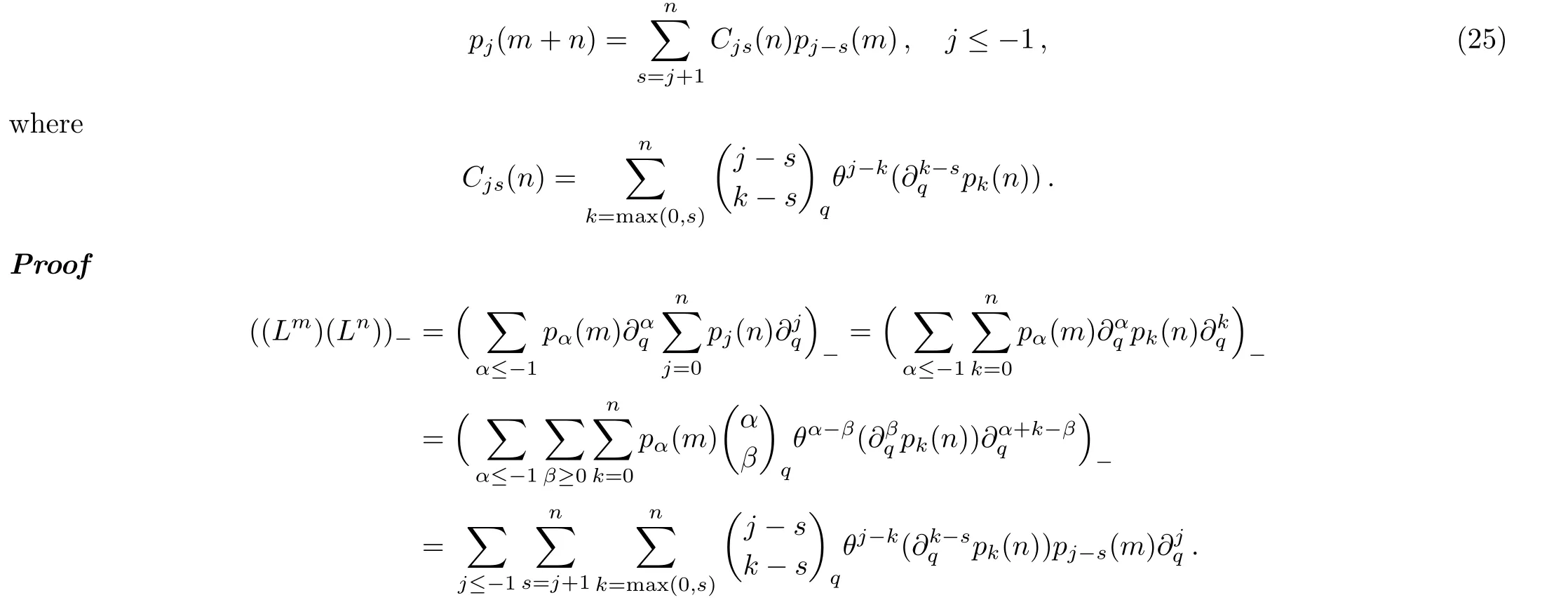
Since(Lm+n)−=((Lm)(Ln))−,comparing withyields the Lemma 1.

Lemma 2

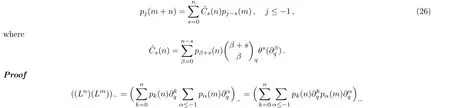
Since

Theorem 5Then-reducedq-KP hierarchy possess a recursion operator Φ(n)such that

fork=0,1,2,...andm,n=1,2,3,...

ProofNote that(Lm+n)−=((Lm)(Ln))−=((Ln)(Lm))−,Eq.(25)in Lemma 1 and Eq.(26)in Lemma 2 forj=−1,−2,...,−ntogether give the next equations.

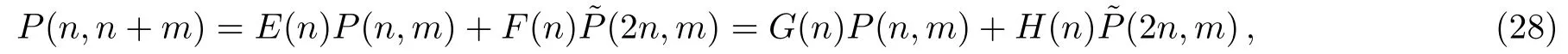
where

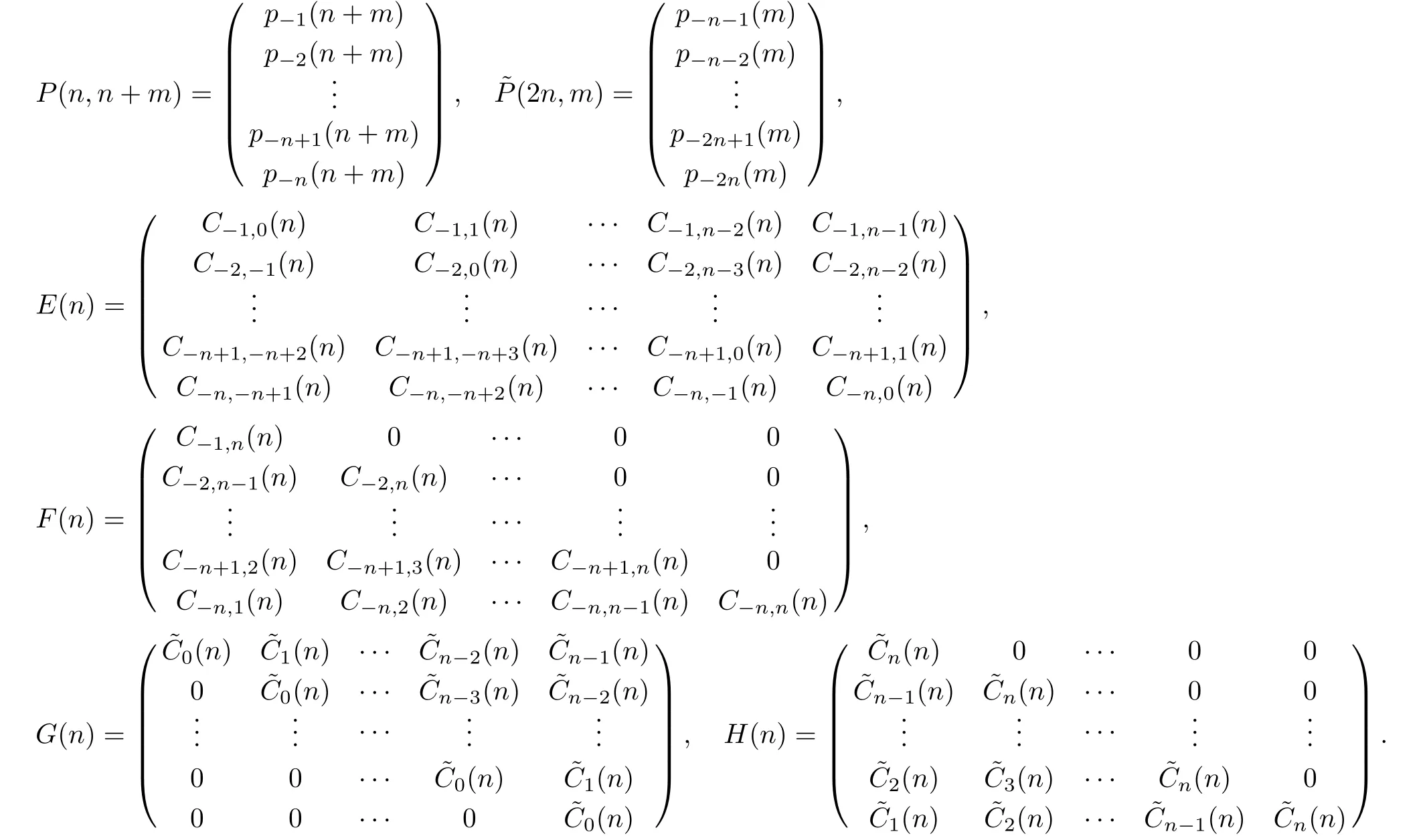
Then we obtain

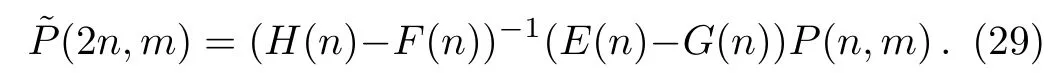
Inserting the vector

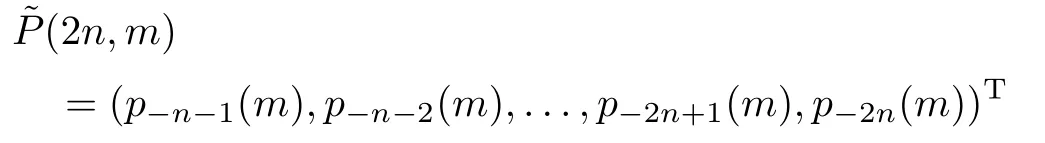
from Eq.(29)into Eq.(28),i.e.

with

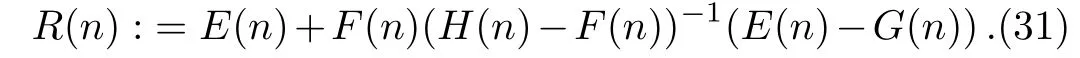
Introducing

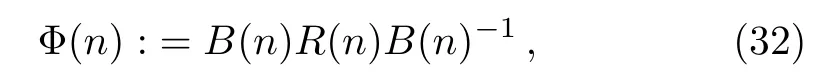
whereB(n)is the same in Theorem 4.Finally,the recursive scheme for the Lax equations of then-reducedq-KP hierarchy could be written out as

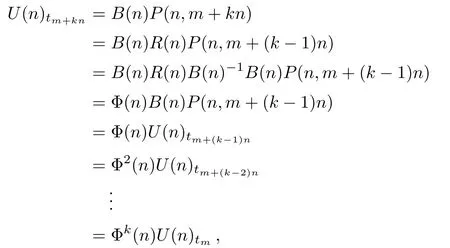
fork=0,1,2,...andm,n=1,2,3,...

Remark 2From Theorem 5 one can find that the recursion operator Φ(n)for then-reducedq-KP hierarchy cannot be reduced to the classical situation asq→1.The reason is that in general we cannot letθ=1 i.e.θ(f)=fin the recursion operator because there is(θn−1)−1in the(H(n)−F(n))−1of Φ(n).Therefore,we can not think that the recursion operator Eq.(32)is aq-extension of the recursion operator of the KP hierarchy.[20]

4 Conclusions and Discussions

To summarize,we have derived two general expressions of the fl ow equations of theq-KP hierarchy in Eqs.(17)and(22)in Theorem 1 and Theorem 3 respectively.We have pointed from these general expressions that the main difference between the fl ow equations of the KP hierarchy and theq-KP hierarchy is due toq-binomial and the action ofq-shift operatorθ,which reflects an essential character of quantum calculus in some senses.The another main result is a general formula of the recursion operator for the fl ow equations of theq-KP hierarchy under thenreduction,which is given in Theorem 5.We would like to stress that the recursion operator Φ(n)for then-reducedq-KP hierarchy cannot be reduced to the classical situation asq→1,which shows that the recursion operator Eq.(32)is not a q-extension of the recursion operator of the KP hierarchy.[20]These results also show thatq-KP hierarchy is not a trivial formalism generalization of the KP hierarchy,and thus it deserves further investigation in the near future.

Acknowledgments

One of the authors(K.T.)is supported by Erasmus Mundus Action 2 EXPERTS and would like to thank Professor Jarmo Hietarinta for many helps.

[1]E.Frenkel,Int.Math.Res.Notices 2(1996)55.

[2]J.Mas and M.Seco,J.Math.Phys.37(1996)6510.

[3]Z.Y.Wu,D.H.Zhang,and Q.R.Zheng,J.Phys.A:Math.Theor.27(1994)5307.

[4]P.Iliev,J.Phys.A:Math.Theor.37(1998)241.

[5]P.Iliev,Lett.Math.Phys.44(1998)187.

[6]P.Iliev,J.Geom.Phys.35(2000)157.

[7]M.H.Tu,Lett.Math.Phys.49(1999)95.

[8]K.Takasaki,Lett.Math.Phys.72(2005)165.

[9]J.S.He,Y.H.Li,and Y.Cheng,SIGMA 2(2006)060.

[10]R.L.Lin,X.J.Liu,and Y.B.Zeng,J.Nonlinear Math.Phys.15(2008)333.

[11]K.Takasaki,J.Geom.Phys.59(2009)1244.

[12]K.L.Tian,J.S.He,and Y.Cheng,AIP Conf.Proc.1212(2010)35.

[13]A.Klimyk and K.Schmüdgen,Quantum Groups and Their Represntaions,Springer,Berlin(1997).

[14]V.Kac and P.Cheung,Quantum Calculus,Springer-Verlag,New York(2002).

[15]E.Date,M.Kashiwara,M.Jimbo,and T.Miwa,Transformation Groups for Soliton Equations,inNonlinear Integrable Systems-Classical and Quantumtheory,World Scientifc,Singapore(1983)39-119.

[16]L.A.Dickey,Soliton Equations and Hamiltonian Systems,2nd ed.NJ:World Scientifc,Singapore(2003).

[17]S.W.Liu and Y.Cheng,J.Phys.A:Math.Theor.43(2010)135202.

[18]H.M.Li,Y.Q.Li,and Y.Chen,Commun.Theor.Phys.62(2014)641.

[19]R.G.Zhou and J.Chen,Commun.Theor.Phys.63(2015)1

[20]W.Strampp and W.Oevel,Lett.Math.Phys.20(1990)195.

[21]M.Gurses,A.Karasu,and V.V.Sokolov,J.Math.Phys.40(1999)6473.

[22]D.J.Zhang and D.Y.Chen,J.Phys.Soc.Jpn.72(2003)448.

[23]J.S.He,J.Y.Tu,X.D.Li,and L.H.Wang,Nonlinearity 24(2011)2875.

[24]Q.S.Cheng and J.S.He,Commun.Theor.Phys.58(2012)631.