基于正交灰关联分析的橡胶改性沥青研究

王　丹, 李　映

(1.黄河交通学院， 河南 焦作　454950；　2.核工业西南勘察设计研究院有限公司， 四川 成都　610061)



基于正交灰关联分析的橡胶改性沥青研究

王丹1, 李映2

(1.黄河交通学院， 河南 焦作454950；2.核工业西南勘察设计研究院有限公司， 四川 成都610061)

[摘要]针对目前橡胶改性沥青改性效果评价指标多，不统一的情况，为了提高橡胶改性沥青整体性能以及提出更为合理的评价方法，首先采用正交设计试验方法配制了4因素3水平的9种橡胶改性沥青，分别测试软化点、锥入度、延度和黏度4项技术指标，进而采用灰关联分析法分析各项指标在橡胶改性沥青改性效果评价中重要性比例，计算综合评分排出4个因素对橡胶沥青改性效果影响的主次顺序，选出最优组合方案。试验结果表明：胶粉掺量对橡胶改性沥青的改性效果影响最大，沥青品种次之，然后是胶粉目数，PE掺量的改性效果最差；在3#沥青中掺加20%的60目橡胶粉和1%的PE具有较好改性效果，为最优组合方案。

[关键词]橡胶粉； 改性沥青； 正交设计； 灰关联分析； 最优组合

0引言

近些年，随着橡胶粉生产的积极发展以及沥青路面结构研究的深入，橡胶粉作为一种能显著改善沥青路面性能(抗滑耐磨、低噪声等)的新型道路建筑材料，在道路建设中逐渐广泛应用[1-3]。但是，橡胶改性沥青的改性效果不是由单一指标决定的，通常由软化点、锥入度(概念同针入度，由于橡胶改性沥青中含有橡胶颗粒，针入度试验的标准针针尖太细，针扎在橡胶颗粒上和不扎在橡胶颗粒上的误差比较大，国外许多试验是采用锥人度来代替针人度，所以本次试验也采用锥入度试验[4])、延度、黏度等多项评价指标共同作用，因此，如何平衡橡胶改性沥青的各项指标以及评价其改性效果成为研究的重点和难点。本文综合考虑沥青种类、胶粉目数、胶粉掺量和PE掺量等因素，采用正交设计试验法[5]进行4因素3水平的L9(34)正交试验，以精简试验次数。通过灰关联分析方法[6-7]对试验结果进行分析，评选出最优组合方案。

1原材料性质

① 沥青： 基质沥青为金陵70号沥青，通过添加不同掺量的RET成为性能不同的改性沥青，其基本性能指标如表1所示。

② 橡胶粉： 本次试验中所使用的橡胶粉是由廊坊市赫维节能材料提供的，胶粉细度分别为40目、60目、80目，主要成分为橡胶(含量45%～55%)，炭黑(含量15%～25% )。废旧胶粉掺量分为10%、15%、20%共3种。

③ PE改性剂由重庆鑫路洁公司提供。本文中提到的掺量均采用外掺法。

表1 试验品种沥青基本性能指标Table1 Performancetestspeciesofbasicasphalt指标1%RET1.5%RET2%RET25℃针入度/(0.1mm)软化点/℃135℃粘度/(Pa·s)延度5℃10℃cmRTFOT后延度/(10℃)/cm61.56159.559.164.266.51.0751.7612.3875.26.16.312.211.310.89.29.710.2

2试验方案设计

2.1正交设计方案

正交设计是从多因素试验次数众多的全面试验中挑选部分具有代表性的点进行试验，正交设计具有“均匀分散、整齐可比”的优点，主要包括试验设计和数据处理两部分。具体设计步骤如下：

① 明确试验目的，确定考察指标。

本次试验是以提高橡胶改性沥青改性质量为目的，选取的考察指标有软化点(℃)、锥入度(0.1 mm)、延度(5℃)和黏度(135℃)等4个指标。

② 定因素、选水平、编制因素水平表。

影响试验结果的因素为试验沥青的品种、胶粉目数、胶粉掺量、PE掺量。各因素均取3个水平。

由上列出四因素A、B、C、D的3水平表，如表2所示。

③ 列出正交表L6(34)及试验组合方案。

试验组合方案见表3所示。

2.2正交试验结果

按照对应的试验组合方案进行试验，试验结果见表4所示。

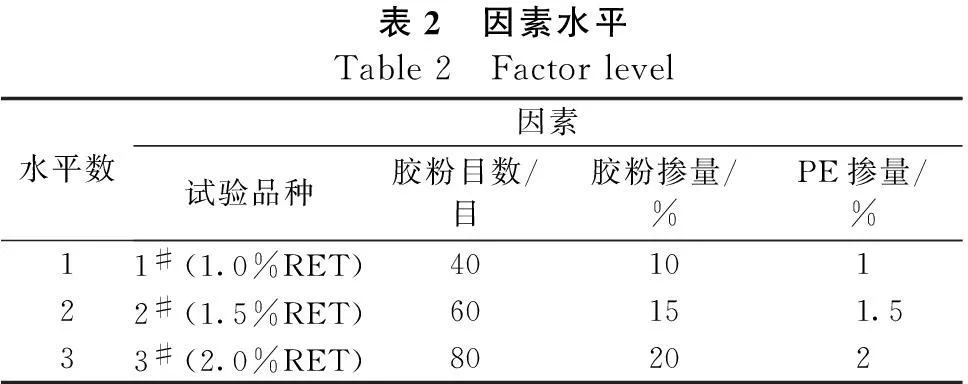
表2 因素水平Table2 Factorlevel水平数因素试验品种胶粉目数/目胶粉掺量/%PE掺量/%11#(1.0%RET)4010122#(1.5%RET)60151.533#(2.0%RET)80202

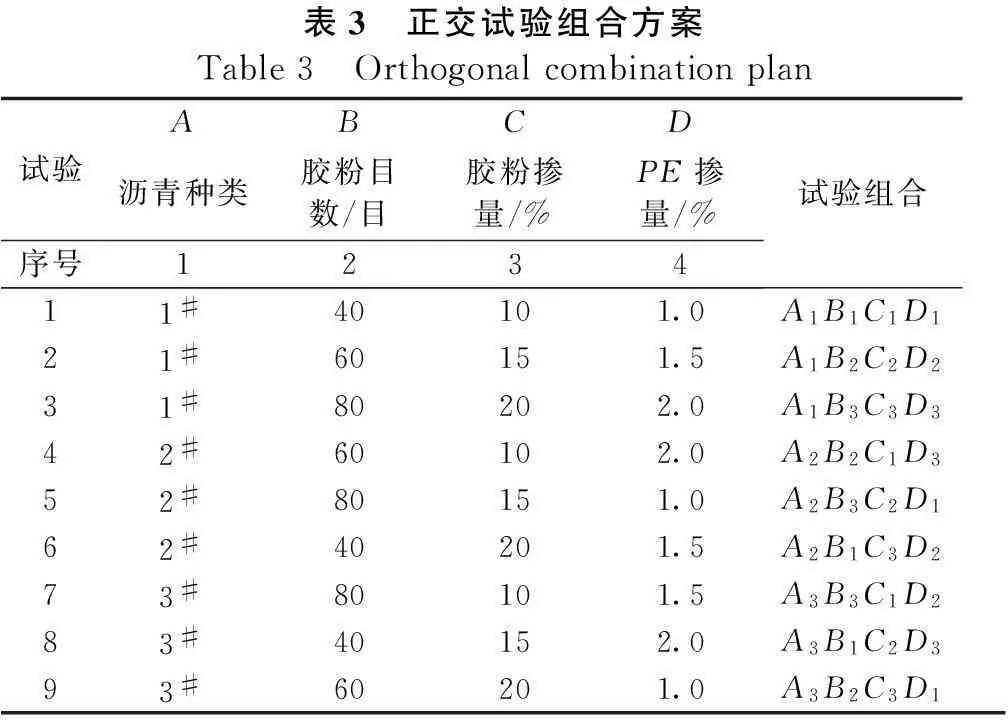
表3 正交试验组合方案Table3 Orthogonalcombinationplan试验序号ABCD沥青种类胶粉目数/目胶粉掺量/%PE掺量/%1234试验组合11#40101.0A1B1C1D121#60151.5A1B2C2D231#80202.0A1B3C3D342#60102.0A2B2C1D352#80151.0A2B3C2D162#40201.5A2B1C3D273#80101.5A3B3C1D283#40152.0A3B1C2D393#60201.0A3B2C3D1

表4 试验结果Table4 Testresults序号软化点/℃锥入度/(0.1mm)延度(5℃)/cm黏度(135℃)/(Pa·s)169.930.54.83.000278.130.44.16.875385.028.86.013.467477.232.95.02.688574.732.27.37.346683.731.45.611.125768.435.24.72.871878.233.34.06.775978.131.87.114.267

3灰关联分析试验数值

灰色关联分析是依据各因素之间发展趋势的相似或相异程度，即“灰色关联度”来衡量因素间关联程度的一种方法[6]。计算步骤如下：

3.1灰色系统序列

定义灰色系统序列：

设X0=(x0(1)，x0(2)，…，x0(n))为系统特征序列，且：

X1=(x1(1)，x1(2)，…，x1(n))

…………………

Xi=(xi(1)，xi(2)，…，xi(n))

…………………

Xm=(xm(1)，xm(2)，…，xm(n))

X1，…，Xm为相关序列，其中，x0(n)为参考序列，xm(n)为比较因素序列。这里取胶粉掺量为参考序列，即X0=(10、15、20)。

3.2对试验数值进行均值化处理

均值化计算的序列公式如下：

(1)

X0=10/15=0.667

同理可得均值化后的其他数据列。

均值化计算后的数据汇总如表5所示。

表5 均值化数据汇总Table5 SummaryofequalizationX0X1X2X3X40.6670.9080.9590.8890.3951.0001.0140.9560.7600.9051.3331.1040.9061.1111.7720.6671.0031.0350.9260.3541.0000.9701.0131.3520.9671.3331.0870.9871.0371.4640.6670.8881.1070.8700.3781.0001.0161.0470.7410.8911.3331.0141.0001.3151.877

3.3求差序列

i=1,2,3,4,k=1,2,…，9

(2)

即Δ01=(Δ01(1)，Δ01(2)，Δ01(3)，Δ01(4)，Δ01(5)，Δ01(6)，Δ01(7)，Δ01(8)，Δ01(9))。同理可得Δ0i，见表6。

表6 序列差Table6 SequencedifferenceΔ01Δ02Δ03Δ040.2410.2920.2220.2720.0140.0440.2400.0950.2290.4270.2220.4390.3360.3680.2590.3130.0300.0130.3520.0330.2460.3460.2960.1310.2210.5400.2030.2890.0160.0470.2590.1090.3190.3330.0820.544

3.4求两极差

(3)

即，Δmax=0.544Δmin=0.013

3.5求关联系数、关联度及因素所占比例

① 关联系数。

(4)

ρ(0,1)为分辨系数，通常取ρ=0.5去辨识灰关联度最理想[7]。

② 关联度。

(5)

由关联系数、关联度可计算各因素重要性所占比例。

由以上公式可得软化点、锥入度、延度和黏度四个因素的重要性比例，见表7。

表7 关联系数及关联度计算结果Table7 Correlationcoefficientandcorrelationcalculationresultsr0ii=1软化点/℃ i=2锥入度/(0.1mm) i=3延度(5℃)/cmi=4黏度(135℃)/(Pa·s)ζ0i(1)0.55660.50530.57700.5239ζ0i(2)0.99650.90190.55660.7766ζ0i(3)0.56890.40770.57690.4008ζ0i(4)0.46880.44530.53670.4872ζ0i(5)0.94371.00000.45670.9344ζ0i(6)0.55020.46120.50180.7072ζ0i(7)0.57810.35100.60000.5080ζ0i(8)0.98960.91350.55560.7480ζ0i(9)0.48220.47110.80510.3493r0i(关联度)0.68160.55690.57400.6039各指标所占比例/%28.2123.0523.7524.99

3.6试验结果处理

以灰关联分析法为依据，使用各评价指标在评价指标中所占比例，用加权法逐一对试样的多个指标进行综合评分计算，将多指标评价转化为单个指标[8]，进而使得分析计算变得简单方便，然后再利用正交设计试验中的极差分析法得出各因素的主次顺序和最优组合方案。

① 确定bij。

分别计算各试验指标最大值与最小值的差，计作h[9]：

软化点h=85-69.9=15.1；锥入度h=35.2-28.8=6.4；延度h=7.3-4.0=3.3；黏度h=14.267-2.688=11.579利用bij=各指标所占比例/h，计算系数bij(j=1,2,3,4)即bi1=28.21/15.1=1.868；

同理可得bij各值，见表8所示。

② 加权综合评分值[10]。

把多指标转化为单指标Yi，Yi的计算公式如下[8]：

表8 bij值Table8 bijvaluesbi1bi2bi3bi41.8683.6027.1972.158

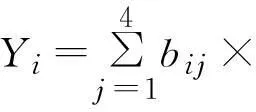
(6)

即:Y1=1.868×69.9+3.602×30.5+7.197×

4.8+2.158×3.000=281.45；

同理可得Y2,…，Y9值。把上面计算的结果列于表9中。

画出同水平综合评分与各因素的水平关系图，如图1所示。

表9 综合评分值汇总Table9 Summaryofcompositedscores试验号试验方案A沥青种类B胶粉目数/目C胶粉掺量/%DPE掺量/%综合评分Yi试验结果1A140101.0281.452A160151.5299.743A180202.0334.764A260102.0304.505A280151.0323.916A240201.5333.777A380101.5294.588A340152.0309.439A360201.0342.32K1915.95924.65880.53947.68T=282.46K2962.18946.56933.08928.09K3946.33953.251010.85948.69K1305.32308.22293.51315.89K2320.73315.52311.03309.036K3315.44317.75336.95316.23R15.419.5343.446.87因素主至次CABD优方案C3A3B2D1

图1　综合评分与各因素的水平关系图Figure 1　Composite scores and each factor levels diagram

从表9及关系图1可得出下列结论：

① 从直接分析来看，九组试验中，第9号试验获得的评分值最高，最优水平组合为A3B2C3D1。

② 由表中的R值大小可以得出四个因素的主次次序(有主到次)为C→A→B→D。也就是说，胶粉掺量对橡胶改性沥青的改性效果影响最大，其次是所用沥青品种，然后是胶粉目数，PE掺量的改性效果最差。

③ 由图1所示，得出最优组合是A2B3C3D3，这个组合在上面的9次试验中没有做过，应安排这个组合的补充试验。

从上面得出的两个最优组合再进行的试验指标对比分析，可得到如表10所示的试验数据。

表10 最优组合试验指标对比Table10 Comparingoftheoptimalcombinationofindicators试验号试验组合方案试验指标软化点/℃锥入度/(0.1mm)9A3B2C3D178.131.810A2B3C3D381.030.5试验指标延度/(5℃)/cm黏度(135℃)/(Pa·s)综合评分7.114.267342.325.410.286322.23

从上面的最优组合对比分析试验中可以看出方案A3B2C3D1优于A2B3C3D3。即橡胶改性沥青的最佳改性效果的最优方案为： 在3#沥青中掺加20%的60目橡胶粉，再加入1%的PE。

4结论

① 针对橡胶改性沥青的多指标评价改性效果的问题，使用正交试验设计和灰关联分析法能够精简试验次数并通过综合评分法选出最优组合方案，回避了只用单一指标带来的不合理性。

② 从改性后的软化点、延度等指标来分析，橡胶沥青的高温稳定性、低温抗裂性等性能指标均得到一定程度的改善。

③ 通过正交试验的综合评分值和灰关联分析结果可以得到各因素对橡胶沥青改性效果的影响程度从大到小依次是胶粉掺量、沥青种类、胶粉目数、PE掺量。即本次橡胶改性沥青的最佳试验组合为：在3#沥青中掺加20%的60目橡胶粉，再加入掺量是1%的PE。

[参考文献]

[1]郭朝阳.废胎胶粉橡胶沥青应用技术研究[D].重庆：重庆交通大学,2008.

[2]王国峰，苏群，张奇，等.应用碳纳米管提高SBS改性沥青及其混合料路用性能的研究[J].森林工程，2014，30(1)：120-

123.

[3]孙红亮，赵曜，朱宇杰，等.透水性沥青混合料配合比设计和路用性能研究[J].森林工程，2015，31(2)：130-134.

[4]李峰,黄颂昌，等.沥青路面灌缝胶性能评价及技术要求[J].交通运输工程学报,2009,9(2) :7-11.

[5]吴贵生.试验设计与数据处理[M].北京:冶金工业出版社,1997.

[6]刘思峰,党耀国,方志耕,等.灰色系统理论及其应用[M] .北京:科学出版社,2004/2008.

[7]邓聚龙.灰色系统基本方法(第二版)[M].武汉：华中科技大学出版社,2005.

[8]张彩利.基于正交灰关联分析的改性沥青性能影响因素分析[J] .公路,2009(11)：191-195.

[9]肖敏敏.灰关联分析在废胶粉改性沥青试验中的应用[J].工业建筑,2009,39(S).

[10]邱轶兵.试验设计与数据处理[M].合肥:中国科学技术大学出版社,2008.

Based on the Orthogonal Grey Relation Analysis of Rubber Modified Asphalt Study

WANG Dan1， LI Ying2

(1.Hanghe Jiaotong University， Jiaozuo， Henan 454950， China；2.Southwest Geotechnical & Design Insfitute of China Nuclear Industry， Chengdu， Sichuan 610061， China)

[Abstract]Aiming at the current situation of more but non-uniform evaluation indexes of rubber modified asphalt modification effect. In order to improve the overall performance of the rubber modified asphalt and made more reasonable evaluation method. Firstly, nine kinds of rubber modified asphalt with four factors and three levels are compounded using orthogonal design method, and four technical indicators including softening point, penetration, ductility and viscosity are tested. Then the importance proportion of every indicator to modification effect is analyzed using gray relational analysis method, and the sequence of four factors affecting on rubber modified asphalt effects after the composite score is calculated to select the optimal combination scheme. The result shows that powder dosage make most impact on modification effect of rubber modified asphalt, followed by varieties of asphalt, then is the powder mesh, PE dosage provides the weakest modification effect. The optimal combination of solutions the 3# asphalt mixed with 20% of 60 mesh rubber powder and 1% of modified PE.

[Key words]rubber powder; modified asphalt; orthogonal design; gray relational analysis; the optimal combination

[中图分类号]U 414.1

[文献标识码]A

[文章编号]1674—0610(2016)02—0256—04

[作者简介]王丹(1989—)，女，河南商丘人，在读硕士研究生，主要研究方向路面材料。

[收稿日期]2014—04—04