落实“四基”重在渗透数学思想

2016-05-28黄奖英

广西教育·A版 2016年1期

关键词：四基数学思想

黄奖英

【关键词】数学思想落实四基

分层渗透

【中图分类号】G 【文献标识码】A

【文章编号】0450-9889（2016）01A-

0023-01

新课标明确提出“四基”的培养目标，但在教学实践中，大部分教师对基本思想和基本经验的理解不够透彻，导致“四基”并不能有效落实。那么，基本思想和基本经验在“四基”中扮演什么角色呢？有人认为，“四基”是一个互相链接的三维模块，其中“基本活动经验”并不能构成单独维度，而是成为基本知识、基本技能、基本思想方法的填充（如图1）。也就是说，数学思想方法的渗透，成为落实“四基”关键中的关键。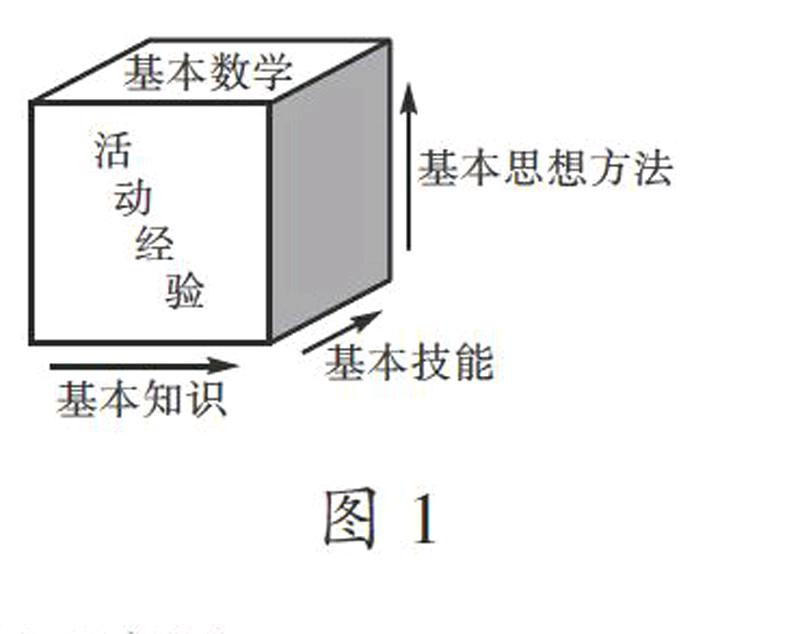

一、经历过程，分层渗透

在小学数学教学中，数学思想方法是一个较为宽泛的概念，要让学生理解这个抽象的概念，需要一个循序渐进的渗透过程。因此，教师要加强过程引导，带领学生经历数学概念的形成过程，分层设置数学思想的渗透，帮助学生感知数学思想方法。

在教学人教版六年级数学上册《圆的面积》时，笔者设置了分层渗透的估算环节。层次一，孕伏极限思想。笔者先出示超市的“幸运大转盘”，让学生根据这个转盘的面积，找出一个合适放置的地方。学生先自行预估，有学生认为可以采用数方格的方法求圆的面积，也就是数出来一行，然后再乘行数；也有学生认为，可以利用正方形的面积来预估，也就是将圆面积与圆内接正方形和圆外切正方形作比较，为极限思想做好孕伏。层次二，渗透转化思想。学生提出将圆转化为已经学过的图形，那么，到底转化为哪种图形呢？学生提出了三种方案，第一种是将圆转化为正方形，但剩下的部分没法转化为已经学过的图形；第二种是将圆转化为几个相等的小扇形，但扇形是没有学过的；第三种是将圆沿着半径等分成4等份，拼成一个近似的平行四边形。此时笔者引导学生针对三种方案展开对比，引导思考：到底哪一种方案更好？学生讨论交流后排除了前两种，选择第三种方案。层次三，明确方法，体验转化思想和极限思想。学生认为，要让圆更接近平行四边形，就要将圆等分的份数增多。接着笔者通过电脑演示，将圆等分为32份、64份……学生发现，圆逐渐转化成了长方形。

这样的教学环节，教师借助分层渗透，让学生一步步体会到极限思想和转化思想，并通过电脑展示，将整个过程呈现出来，使学生直观观察到并经历了化曲为直、化圆为方的转化过程，充分体会了逐渐逼近的极限思想。

二、对比联系，凸显本质

在小学数学教学中，形式的运动变化有利于学生“透过现象看本质”。因而，教师要加强对比联系，让学生深入这一数学过程，凸显数学本质。

在教学人教版五年级数学上册《平行四边形的面积》时，笔者指导学生思考：如何将平行四边形转化成我们学过的已知图形？学生认为，要将高剪下来，然后进行拼接。此时笔者故意将平行四边形剪成了平行四边形，追问学生：为何会这样？学生指出，这是没有沿着高剪开导致的。笔者让学生展开自主操作。学生通过画一条高，沿着高剪开，而后将剪下来的部分拼接到另一边，将平行四边形转化为长方形。接着笔者追问：是不是所有的平行四边形都可以转化为长方形？学生验证确认后，笔者再让学生展开对比联系：转化后的长方形和平行四边形相比，什么发生了变化？学生指出，转化后的长方形面积没变，长没变，但高变了；也有学生指出，长方形的周长变了，名称变了。到底有什么变化呢？学生总结后指出，转化后平行四边形的底边和高变成了长方形的长和宽。由此，学生对转化思想有了本质上的理解。

三、加强应用，整体感知

数学教学的本质，是要培养学生的数学思维，将现实问题通过数学思维展开思考，并最终解决问题。因此，教师要加强实践应用，带领学生整体感知数学思想。

在教学人教版五年级数学上册《三角形的面积》时，笔者设计了这样一道练习题（如图2）：两个正方形中有一个三角形，算出阴影部分的面积。学生很快找到了问题的关键，认为要求阴影三角形的面积，就要找出三角形的高，但是三角形的高如何找呢？笔者引导学生从转化思想入手，先找出已知的条件，然后根据已知条件，寻找未知条件的突破。学生先根据正方形的边长，确定和三角形的关系。学生发现，三角形的高就是两个正方形的边长之和。由此，自然而然地求出了三角形的面积。