弱刚度环类零件装夹变形的研究
2016-05-27卢继平张程焱曹博然焦思程
王 欢,卢继平,张程焱,曹博然,焦思程
(北京理工大学 机械与车辆学院,北京 100081)
弱刚度环类零件装夹变形的研究
王欢,卢继平,张程焱,曹博然,焦思程
(北京理工大学 机械与车辆学院,北京 100081)
摘要:弱刚度环类零件车削加工易变形,在装夹过程中产生的弹性形变是造成加工后形状误差的一个重要原因。将普通卧式车床上所使用的三爪自定心卡盘改良为扇形卡盘,分别计算了2种装夹方式产生的理论变形量,建立了影响装夹变形的各个因素与变形量之间的函数关系,根据计算结果得到了扇形卡盘的最优结构参数,并通过有限元仿真实验,针对齿圈这类典型的弱刚度件的2种装夹方式进行了对比验证,为减小弱刚度环类零件的装夹变形提供了理论基础。
关键词:环类零件;弱刚度;单位载荷法;扇形卡盘
零件加工精度包括尺寸精度、形状精度和位置精度。环类薄壁件的整体刚度较差,在装夹过程中由于夹紧力和加紧方式安排不当,会造成较大的弹性变形,从而使零件加工之后产生较大的形状误差,严重影响了这类工件的加工精度[1-2]。M. Maraĉeková等研究了夹紧力对空心薄壁筒加工后圆度误差的影响,并使用新的装夹系统来减小圆度误差[3]。石振鹏对薄壁件的车削工艺进行了优化,提出了通过减小夹具和工件的高度差以保证加工质量[4]。陈树峰等分析了薄壁套筒的装夹变形并给出了加工误差与卡爪数之间的关系式[5]。根据现有研究成果和实际生产加工中的经验,可以得到如下几种改善装夹变形的方法[6]:1)确定大小与作用位置合适的夹紧力;2)增加夹持点的数目;3)设计某种特定结构的夹具元件。
在加工发动机传动系统中所需的端盖、齿圈和行星架等关键零件时,通常采用带三爪自定心卡盘的普通卧式车床。由于三爪自定心卡盘具有自定心功能,所以在装夹零件时,加紧位置和夹持点的数目是相对固定的。在这种情况下,应通过设计某种结构参数的卡爪才能够改善由装夹引起的变形。将普通的三爪自定心卡盘的卡爪改良为扇形卡爪(见图1),增大卡爪与工件的接触面积,对工件形成包络,在这种装夹情况下进行车削加工,工件的形状误差会有所改善。

图1 扇形卡盘
本文利用单位载荷法从弯矩的角度分析这种改进对变形量的影响,通过计算扇形卡盘的装夹变形系数得出使变形量最小的扇形圆心角大小,用齿圈这一典型弱刚度环类零件的仿真实验来验证扇形卡盘减小装夹变形的效果。
1环类零件装夹变形量的计算分析
1.1三爪自定心卡盘夹持工件变形量的计算
普通车床上三爪自定心卡盘夹持环形薄壁工件的受力状态如图2所示。3个夹头端点施加3个互成120°的径向集中力P,圆环的半径为R,工件材料的弯曲刚度为EI,其中,E为零件材料的弹性模量,I为零件截面的惯性矩。
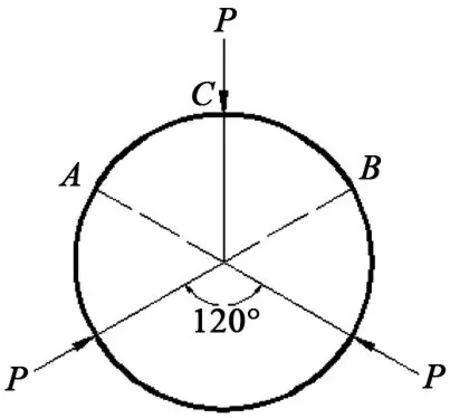
图2 三爪卡盘受力状态
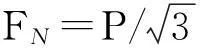
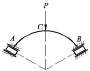
图3 约束转化
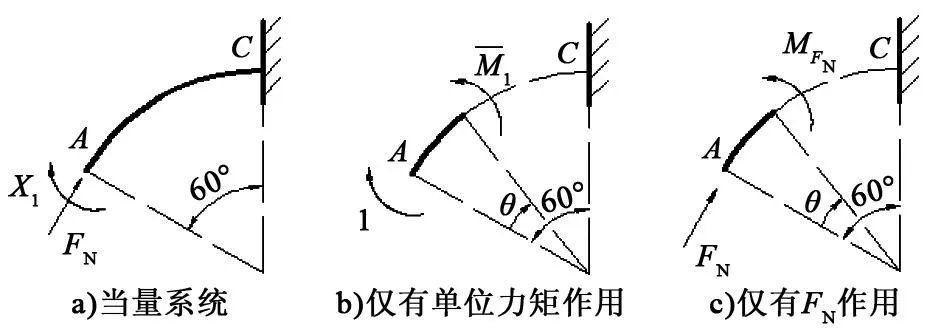
图4 一次静不定问题
力法正则方程为:
δ11X1+Δ1F=0
式中,X1为A截面处的弯矩;δ11为单位载荷(力或力矩)作用下的变形;Δ1F为力F作用下的变形。
当仅有单位力矩作用时:
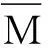
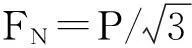
MFN=-FNR(1-cosθ)
将δ11与Δ1FN代入正则方程得:
由对称性可知,A、C两处没有转动,只有沿径向的移动。利用单位载荷法,求解A、C两处的变形(见图5)。其中,C处的位移可转化为A处反向的位移。
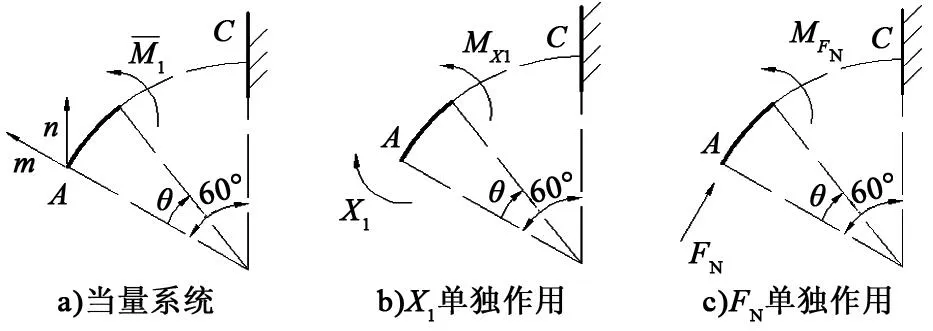
图5 单位载荷法求A、C截面位移
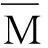
ΔA=Δ1X1+Δ1FN=
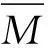
1.2扇形卡盘夹持工件变形量的计算
将三爪自定心卡盘的夹头改为扇形(见图6),每个扇形夹爪对应的圆心角为60°,3个夹头互成120°分布,每个夹头处施加载荷集度为q的均布载荷,圆环半径为R,工件材料的弯曲刚度为EI。
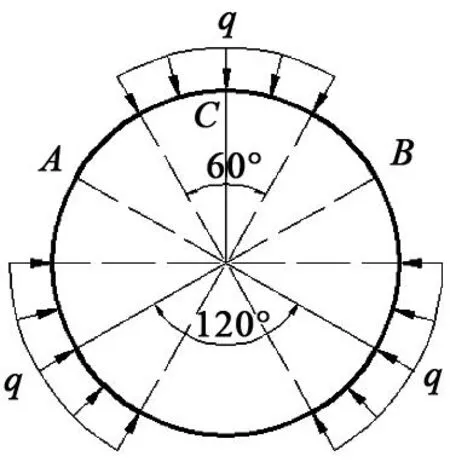
图6 扇形卡盘受力情况
利用对称性,取1/3圆弧(见图7)。由力的平衡条件,得出A、B处的法向约束力FN与载荷集度q的等式关系为:
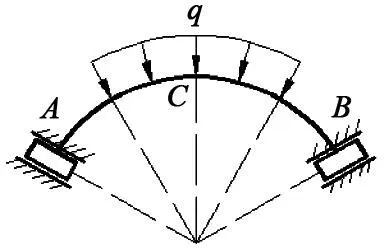
图7 约束转化
该结构可简化为一次静不定问题(见图8)。
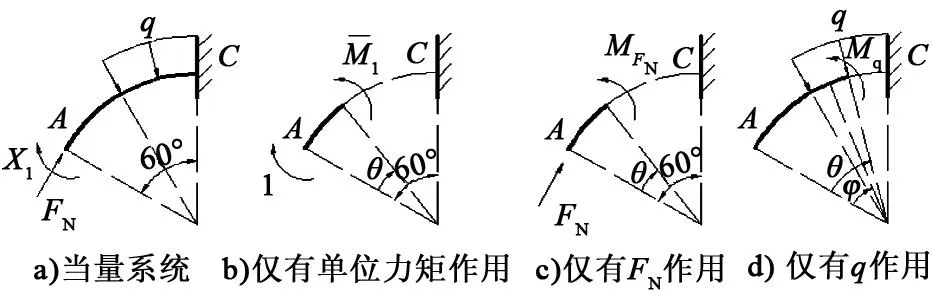
图8 一次静不定问题
力法正则方程为:
δ11X1+Δ1F=0
式中,X1为A截面处的弯矩;δ11为单位载荷作用下的变形;Δ1F为力F作用下的变形。
当仅有单位力矩作用时:
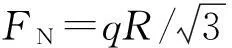
将δ11、Δ1FN和Δ1q代入正则方程得,
由对称性可知,A、C两处截面没有转动,只有沿径向的移动。利用单位载荷法求解A、C两处的变形。其中,在求解C截面处的位移时,可将C处位移转化为A处与之反向的位移。
单位载荷法求A、C两截面处位移如图9所示。
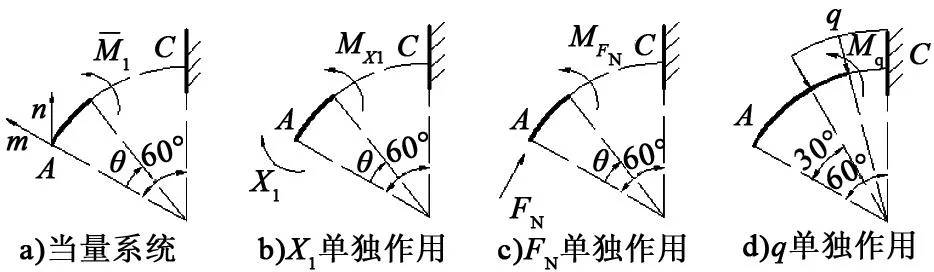
图9 单位载荷法求A、C两截面处位移
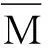
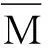
当P=qR时,即分布载荷q在竖直方向上的合力与集中载荷P大小相等时,通过计算结果可以比较出在A、C两处,普通卡盘的装夹变形量大于扇形卡盘的装夹变形量。
1.3扇形卡盘结构参数的优化
根据上述对扇形卡爪装夹环类零件产生的变形量的分析,可以得出A截面变形量的函数关系式:
这他是知道的。不久他就会走到那块“小棍子地”。他觉得它就在左面的什么地方,而且不远——可能翻过下一座小山头就到了。
y=[0.892sinx-0.547cosx-0.25sinxsin2x+
式中,x为扇形卡爪对应的圆心角;P为夹紧力值;R为环类零件的半径。
从函数式中可以看出,变形量与夹紧力的大小呈线性关系,也与环类零件的结构尺寸、截面形状以及零件材料的弹性模量有关,同时与夹具的结构尺寸、加工部位以及粗精车方式有关。
0.25sinθsin2θ+0.217cosθsin2θ+
式中,θ为扇形卡爪对应的圆心角。
针对特定的环类零件,PR3/(EI)为定值,此时变形系数k的大小决定了变形量。
扇形卡盘装夹环类工件的变形量随扇形卡爪圆心角变化的趋势如图10所示。当扇形卡爪的圆心角为0.88 rad时,变形系数将产生一个极小值,此时零件的装夹变形量最小;当θ≥1.25 rad时,扇形卡盘的变形系数大于普通卡盘,说明此时随着卡盘与工件接触面积的增大,由于二者精确配合的难度增加,变形量会增大。需要注意的是,当θ≤0.35 rad时,扇形卡爪与零件的面接触较小,此时近似于普通卡爪的线接触,因此,该函数式不适用于扇形卡爪角度较小的情况。
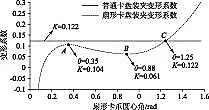
图10 变形系数变化曲线
1.4齿圈的有限元仿真验证实验

图11 齿圈的三维模型
对于理论分析得出的结论,可通过有限元仿真进行模拟验证。本文针对齿圈这一典型弱刚度环类零件进行仿真模拟。车辆传动系统中的齿圈属于高精度弱刚度件,其材料为20Cr2Ni4A,三维模型如图11所示,零件图如图12所示。齿圈最大外圆直径为369 mm,加工完成后最小壁厚为11.5 mm,齿圈的直径和壁厚的比值较大,刚度较弱,容易产生变形。
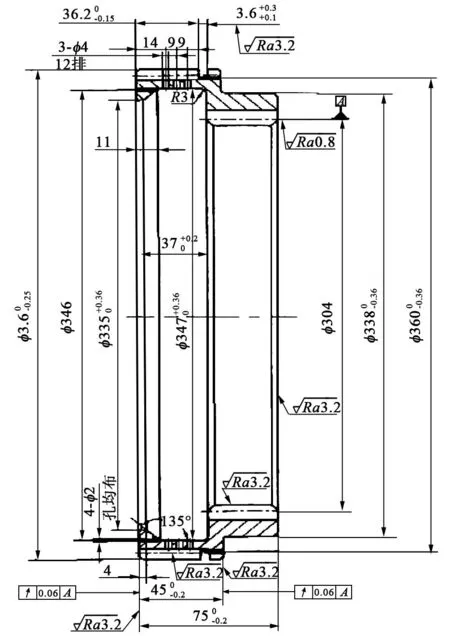
图12 齿圈的零件图
总体来说,齿圈的加工主要分为“锻造制坯→粗车→热处理→精车→滚插齿→磨削加工→修整”这几个工序。在Abaqus6.11中模拟粗车内圆时的装夹变形,仿真结果如图13和图14所示,扇形卡盘的最大装夹变形比普通卡盘减小了26.9%。

图13 普通卡盘装夹变形
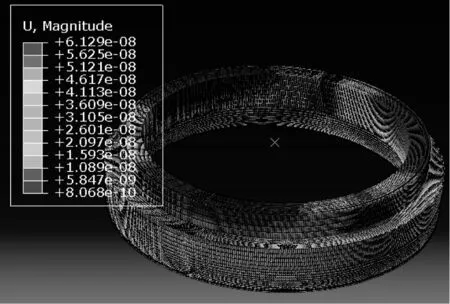
图14 扇形卡盘装夹变形
2结语
通过理论分析和有限元仿真,可以得到如下结论。
1)利用单位载荷法的理论分析,可以定量得出均布载荷作用在环类零件上的变形量小于数值上等效的集中载荷作用的变形量。
2)使用扇形卡盘装夹环类零件的变形量与夹紧力的大小呈线性关系,也与环类零件的结构尺寸、截面形状、零件材料的弹性模量以及变形系数有关。通过分析可知,当扇形卡爪的圆心角为0.88 rad时,变形系数最小,此时对环类零件产生的装夹变形量最小。
3)通过有限元仿真实验可知,与普通三爪自定心卡盘相比,扇形卡盘可以有效地减小装夹变形,从而改善环类零件加工后的形状误差。
参考文献
[1] 王先逵. 机械制造工艺学[M]. 北京:机械工业出版社,2006.
[2] 王三民,陈波,廉继西,等.定力夹具应用技术工艺研究[J].新技术新工艺,2014(6):9-11.
[3] Maraĉeková M, Zvonĉan M, Görög A. Effect of clamping pressure on parts inaccuracy in turning[J]. Technical Gazette, 2012(3):509-512.
[4] 石振鹏. 45Cr淬硬钢薄壁件车削工艺优化研究[D]. 天津:天津大学,2008.
[5] 陈树峰,马伏波. 薄壁工件在夹紧力作用下变形量的计算[J]. 煤矿机械,2005(2):70-72.
[6] 程建明. 控制盘类零件加工精度的理论及其方法的研究[D]. 上海:上海交通大学,2002.
责任编辑郑练
Research on Clamping Deformation of Weak-rigidity Hollow Disk
WANG Huan, LU Jiping, ZHANG Chengyan, CAO Boran, JIAO Sicheng
(School of Mechanical Engineering, Beijing Institute of Technology, Beijing 100081)
Abstract:The weak-rigidity hollow disk is easy to deform when cutting. Clamping deformation is one of the most significant reasons to bring about the form error after machining. The three-jaw chuck is replaced by the fan chuck on the lathe and deformations of the two clamping modes which are calculated separately. A function relationship between the factors influenced on the deformation and the clamping deformation is concluded and the best structure parameter of the fan chuck is optimized. The finite element method is used to compare the two clamping modes by a typical weak-rigidity gear ring. The result provides a basic theory to minimize the clamping deformation of weak-rigidity hollow disk.
Key words:hollow disk, weak-rigidity, unit load method, fan chuck
中图分类号:TH 161+.3
文献标志码:A
收稿日期:2015-11-05
作者简介:王欢(1990-),男,硕士研究生,主要从事先进加工技术及生产系统等方面的研究。
