做好中小学数学教学衔接
2016-05-26张峰
张峰
实现九年义务教育,按照系统论的观点,是一个密不可分的完整体系。为此,要做好中小学数学教学的衔接问题,仍需中小学双边共同努力。作为小学数学教师,我们应抓好以下方面,为小学毕业生迈进中学搭桥铺路。
一、教好数的概念,向学习有理数过渡
数的概念是逐步扩展的。小学主要学习非负整数,直到六年级才认识负数,进入初一年级,正式学习负数,数就扩展为全部有理数。因此,由非负有理数过渡到全部有理数是小学学习数的概念之衔接点。为使学生顺利渡过这一关,应注意以下几点。
1.教学整数的意义时,要注意数的扩展。不能说“自然数叫做整数”或“整数就是自然数”。应按教材中说的“自然数是整数”或更确切地说“自然数是整数中的一部分”,即整数包括自然数,使学生意识到整数内容尚未学完。
2.教学“0”的意义时,讲清“0”是表示一个物体也没有,“0”在数位上表示这位上一个单位也没有,并起着占位的作用。此外,要求学生注意“0”有别的意义,如温度的摄氏0度,时刻的0时,地球经纬线的0度……这里“0”表示一种特殊的量,是界数,为初一年级学习负数打下基础。
3.教学中应注重课本中出现的“用直线上的点表示数”,如:
教师应十分重视类似内容,为学习数轴打好基础。
4.数学中应注重课本中出现的一些意义相反的量。如:增加与减少,增产与减少,上升与下降,向东与向西,前进与后退,等等。让学生对这些意义相反的量有些了解,为学生七年级进一步学习负数打好基础。
二、教好“用字母表示数”,向学习代数过渡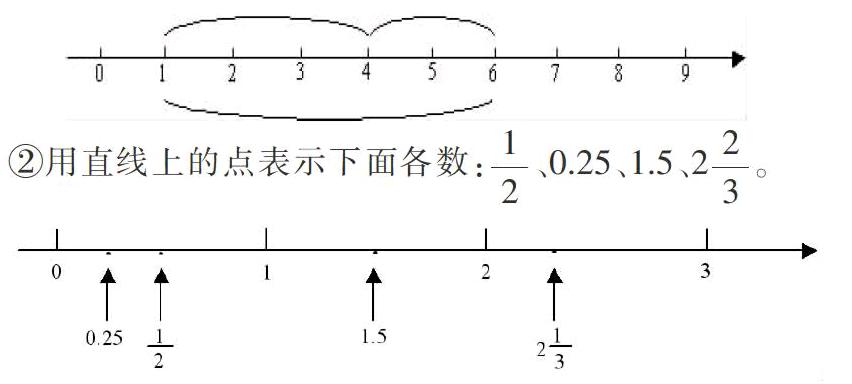
从算术到代数是数学的一次飞跃。“用字母表示数”是学生学习代数知识的入门内容,是学习代数知识的基础,这部分知识对于学生来说较抽象,掌握有一定难度。学生在以往的数学学习中,接触到的都是具体的数,而现在要学会用字母即抽象的符号代表具体情境中的数量,用含有字母的式子表示简单的数量关系,这是从具体形象思维到抽象逻辑思维的一次过渡,也是思维的一次飞跃。其中,从确定的数→用字母表示数→引进代数式,是一个很重要的内容。如:
在教学中,教师要利用学生熟悉的生活情境,引导学生用字母表示数,体会字母的作用,使学生自然萌生出用字母表示数的需要,并渗透归纳猜想、数形结合等数学思想方法,从而为初中代数学习打下坚实的基础。
三、教好简易方程,向代数解法过渡
小学一至四年级,学生解答应用题习惯用算术解法,把未知量放在特殊的位置,用已知量求出未知量,这对进入中学学习代数解法很不利。故而在教学“简易方程”一章时,应让学生掌握解题要领,即把未知量用字母表示,并且和已知量放在平等的位置上,设法找出等量关系,列出方程,求出未知量。主要抓好:
1.用含有字母的式子表示数量关系。如:比x少5的数,表示为x-5。
2.用方程式表示数量关系。如:比某数的3倍少2是25,求某数。表示为3x-2=25等。
3.分析题意,依条件找等量关系,列出方程,这是列方程解应用题最重要之处。如何找到等量关系是关键所在。常用以下方法:①抓住关键词语,如:一共,还剩,多(少),增产,节约等。②依题意画图,直观演示题中的数量关系,具体明确,容易找到等量关系。③将题中的条件与问题列成表,清楚明白,这样也容易找到等量关系。
四、教好几何初步知识,向学习平(立)几过渡
小学几何初步知识,是中学平面几何和立体几何的基础,为了搞好衔接,教学中应注意以下方面。
1.重视几何图形知识的教学。几何图形是几何学研究的对象,是几何学的基础。几何学知识即从最基本的几何图形出发,用推理方法建立起来的关于几何图形间的联系和规律的系统。因此,小学几何初步知识的线、角、形、体的认识,在教学中应该以直观描述图形的特征为主,不给学生下严格的定义,但必须通过形象直观让学生形成关于几何图形的正确表象。
2.重视求积公式的教学。在小学阶段,面积、体积公式的导出,主要是利用演示、实验的方法。如数方格,把所示图形割拼转变成已学图形等,而缺少必要的论证。在使用公式时,要求学生弄清每一步的理论依据。如:三角形面积=底×高÷2,“底×高”求出两个完全一样的三角形拼成的平行四边形面积,“除以2”即求出其中一个三角形的面积。这样,从小培养学生说话有依据,计算有道理,为今后中学学习几何证明打下坚实的基础。
此外,在推导公式时,应注意引导学生多方面思考,同一图形用不同的方法导出其公式,可以发展学生的发散思维,培养学生的思维品质。
教学中,教师应高瞻远瞩,掌握知识的整体性、连续性、独立性和阶段性,把握中小学的相关知识的衔接处,恰当而正确地为学生搭桥铺路、清除障碍,使学生的认识与思维畅通无阻,顺利提高学生的科学文化素养。
