考虑Hub网络拥堵的轴辐式网络优化

杨 斌，邓志慧，胡志华

(上海海事大学 物流研究中心，上海201306)

考虑Hub网络拥堵的轴辐式网络优化

杨 斌，邓志慧，胡志华

(上海海事大学 物流研究中心，上海201306)

在轴辐式网络背景下，枢纽节点通过集散货物，产生规模经济效应来降低成本。但同时也会增加Hub网络拥堵的可能性和成本的增加。首先，为缓解Hub网络拥堵并降低其造成的经济损失成本，提出与轴辐式网络节点流量相关的拥堵成本函数。其次，在保证轴辐式网络节点正常货物运输的前提下，最大限度的平衡货物运输规模经济效应和产生的Hub网络拥堵成本，建立混合整数非线性规划模型，以最小化运输成本、建设成本和拥堵成本为目标。最后，引用实际算例验证Hub网络拥堵对网络优化的影响与模型的合理性。对于未来如何平衡规模经济效应和Hub网络拥堵的轴辐式网络优化有重要的参考价值。

交通运输工程；轴辐式网络；网络优化；枢纽选址；Hub网络拥堵；混合整数非线性

0 引 言

轴辐式网络(Hub-and-Spoke network)是指由非枢纽点(Spoke)与枢纽点(Hub)通过一定方式连接而成的运输网络，在军事、航空、通讯、邮政、旅游等行业中运用广泛。在轴辐式网络中，在运送过程中，OD流首先汇聚到相应的枢纽点，再由枢纽点转运至指定的辐节点，这一方式依靠枢纽点的集货和散货功能，增大了运输网络中干线的货物流量，从而形成了枢纽之间的规模经济效应，降低了运输成本。但在实际情况中，每个枢纽都具有相应的最大能力水平，反应其对集中到该枢纽的货流的处理能力。当流过该枢纽的货流量超过其最大能力水平，就会导致枢纽的处理不及时，让许多货物停留在枢纽之间的干线运输上，造成Hub网络的拥堵，从而影响货物的正常运输，增加总成本。因此考虑Hub网络拥堵的轴辐式网络优化问题是非常必要。在轴辐式网络设计和优化中必须考虑Hub网络拥堵因素。如何规划轴辐式物流网络，确定枢纽位置和数量，确定非枢纽节点和枢纽的连接关系是轴辐式网络设计研究的重心。枢纽网络中的中位问题最早由M.E.O’Kelly[1-2]提出，建立了二次规划模型，并利用启发式算法进行求解。ZPFEL G等[3]认为轴辐式网络设计的关键是确定枢纽节点。T.MEYER等[4]设计了两阶段算法求解单分配的P枢纽选址问题。C.C.LIN[5]则研究星型二级网络的设计问题，建立了有向网络配置的整数规划模型。针对轴辐式网络设计中的不确定性问题，S.A.ALUMUR等[6]研究了不确定性交通运输方式下的枢纽网络设计问题，建立混合整数规划模型，并设计启发式算法进行求解。陆化普等[7]研究了OD流不确定条件下的离散交通网络设计问题。翁克瑞等[8]分析了轴辐式物流网络的形式和优缺点，并指出了该网络设计应考虑的3个问题：规模效应、确定枢纽的数量与选址、分配物流需求节点与运输路线。翁克瑞[9]提出了轴辐式物流网络中的轴线固定成本的问题，并建立混合整数规划模型和设计拉格朗日松弛算法，并且在扩展问题中引入了“绕道约束”，给出了解决方案。郭建华[10]在分析影响快运网络枢纽节点城市布局的经济因素基础上，利用主成分分析法建立评价模型。崔小燕等[11]针对无容量约束的单分配轴辐式物流网络设计的特点，建立了单分配P-枢纽中位模型，并提出一种基于蚁群算法的启发式算法。

目前拥堵的研究主要集中于分析拥堵产生的原因、提高码头作业效率和优化集疏运体系等3个方向。文献[12-13]对港口拥堵的背景、拥堵特征和原因等进行了分析，同时提出了可能出现的排解港口拥堵的方法。R.C.LEACHMAN等[14]通过排队理论建立了基于进口货量、操作人员和装备能力的“货流—时间”模型，用以预测通过特定港口枢纽的货量和拥堵时间之间的关系，并且以中国至美国间的集装箱水路运输为例对模型进行检验。L.FAN等[15]建立了一个多式联运网络，对美国进口集装箱运输网络的空间竞争性、拥堵状况及货流进行了研究。K.H.KIM等[16]为提高堆场装卸效率，对龙门吊路径优化问题进行了研究，提出了一个混合整数规划模型并且使用动态编程技术求解。X.GUO等[17]提出了一种新的动态码头工作负载分配方法，利用时间分割算法有效地找到了可以随工作负载分配的改变而迅速匹配的时间窗口序列，并且达到了与现有空间分割算法同样的效果。S.CHOO等[18]将港口拥堵作为数学建模的依据之一，综合考虑码头处理单船和多船同时靠泊的情况，研究了码头岸桥调度的优化算法。CHEN G等[19]利用“船舶时间窗口”的概念处理口岸集卡拥堵的问题，采用“削峰填谷”的思想有效地缓解了码头集装箱卡车的拥堵。

综上所述，在国内外，大部分关于拥堵问题的研究主要涉及对拥堵产生的原因、背景及特征等方面进行定性分析，对衡量拥堵造成的损失和影响缺乏定量的依据；笔者对Hub网络拥堵成本进行了量化，建立了与节点流量相关的拥堵成本函数，将拥堵和轴辐式网络结合，针对轴辐式网络中的Hub网络拥堵现象，建立了基于Hub网络拥堵的混合整数非线性模型，并通过目标函数线性化等方法进行模型求解，最后通过算例验证模型的有效性和合理性。在保证网络节点正常运输的前提下，通过确定枢纽节点和辐节点及流量分配，最大限度的平衡货物运输使总成本最小化。这对未来轴辐式网络优化中考虑Hub网络拥堵具有重要的参考价值。

1 考虑Hub拥堵的轴辐式网络模型

1.1 拥堵成本的量化

轴辐式网络通过将多个节点确定为枢纽，辐节点都必须通过枢纽节点进行中转。虽然这个可以在Hub网络中形成规模经济效应，但这样也意味着大量的货流量被集中在干线运输上，当进入枢纽节点的货流量超过最大处理能力时就会形成Hub网络拥堵。拥堵成本的量化就是对拥堵发生时的增加的经济成本进行数学上的表达。

为了将拥堵成本量化，在建立拥堵成本函数之前做出如下假设：拥堵成本只发生在Hub网络中，且无论枢纽节点单日货物流量多少，总量上拥堵成本一直发生；拥堵成本包含直接营运损失及其他各类隐性成本。由拥堵造成的单位时间的经济损失为某一定值，即拥堵成本与延误时间之间成正比关系。图1是延误时间随节点流量变化趋势图[20]：

图1 枢纽节点的流量与延误时间示意Fig.1 Schematic figure of the hub node flow and the delay time

从图1可以看出，延误时间随流量的变化呈指数递增关系。当流量小于一定量时，延误的上升趋势缓慢；当流量超过该值时，延误急剧上升。根据上节的假设，拥堵成本与延误时间成正比，所以也与枢纽节点的流量成正比。故定义描述拥堵成本与节点流量之间的拥堵成本函数为[21]

f(u)=aub

式中：f(u)为拥堵成本；u为枢纽节点的流量(由于采取指数形式表达，为使函数在整体量纲上统一，计算时将u视为无量纲值，仅保留数值关系)；a为有量纲系数；b为正常数且b≥1；参数a=1，b取值不同时的拥堵成本函数见图2[22]。

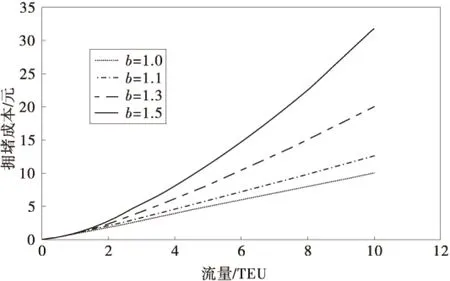
图2 不同参数下的拥堵成本函数 (a=1)

1.2 模型的建立

笔者考虑hub网络拥堵情况，建立混合整数非线性规划模型，目标是平衡hub网络规模经济效应和hub网络拥堵前提下，使总成本最小。结合上节的拥堵成本函数，建立数学模型：

minf=fsetup+fcol+fdist+fhh+∑f(u)

(1)

s.t

∑kxik=1 ∀i,k∈N

(2)

xik≤xkk∀i,k∈N

(3)

∑lyijkl-∑lyijlk=Oixik-∑jWijxjk∀i,k,l∈N

(4)

∑l≠kyijkl≤Oixik∀i,k,l∈N

(5)

∑lyijkl=xik∀i,k,l∈N

(6)

∑kyijkl=xjk∀i,k,l∈N

(7)

∑kxkk=p∀k∈N

(8)

Oi=∑jWij∀i,j∈N

(9)

Di=∑jWji∀i,j∈N

(10)

(11)

yijkl≥0 ∀i,k,l∈N

(12)

目标函数为最小化网络的总成本如式(1)，总成本包括有4个部分，分别为枢纽点的建设成本，货物由起始点运到枢纽点过程中的收集成本，干线运输成本，以及由枢纽点运至目的节点的配送成本。式(2)为节点分配关系约束，表示每一个节点只能作为枢纽节点或是枢纽点的辐节点，不能独立存在；式(3)表示只有当节点k的xkk为1时，即选择节点k作为枢纽节点，才能够将其他节点分配至节点k，否则节点k不能拥有辐节点；式(4)为节点i的货物流量平衡约束；式(5)为辅助约束，用以确保模型在节点距离不严格符合三角形不等式时仍然可以使用；式(6)和式(7)确保任意流经(k,m)的货流(i,j)，节点i和j被分别分配至节点k和m；式(8)保证枢纽节点的数量；节点i的总货物流入量与流出量由式(9)与式(10)得到；xik的0-1约束与yijkl的非负限制如式(11)，式(12)。

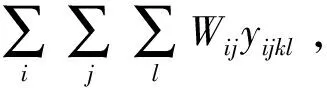
所以原模型可以写为：

minf=fsetup+fcol+fdist+fhh+

∑ka(∑i∑j∑lWijyijkl)b

约束条件仍为式(2)～式(12)。

2 目标函数的线性化

注意到模型的目标函数是一个非线性函数，它会对模型的求解带来很大的困难。基于上一节的讨论，用逐次正切线性化之后再对模型进行求解。表示流经枢纽节点k的货量，对于一个给定的货流 ，拥堵成本函数的正切值可以通过式(13)表示：

(13)

因此f(uk)线性化可以表示为：

(14)

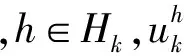
minf=fsetup+fcol+fdist+fhh+

∑kmaxh∈Hk{a(1-b)(∑i∑jWijxik)b+

ab(∑i∑jWijxik)b-1∑i∑jWijxik}

(15)

约束条件仍为式(2)～式(12)。

由于在目标函数线性化的过程中引入了无数的约束变量，为保持问题的等价，模型改为:

f=fsetup+fcol+fdist+fhh+a∑kωk

(16)

约束条件为式(2)～式(12)及：

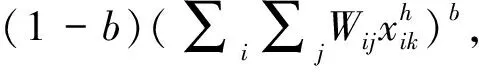
(17)

3 算例分析

3.1 计算实验

为了验证上述所提出的考虑Hub网络拥堵的轴辐式网络优化模型的有效性和合理性，我们使用一个具体的算例进行算例仿真。为了不使计算过程过于复杂，本算例选取了20个节点，由Excel随机生成的横纵坐标值，节点分布如图3，节点之间的OD运输量如表1，求解模型用MATLAB实现。

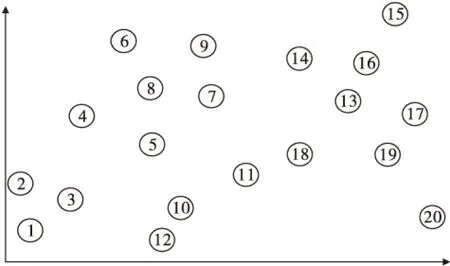
图3 各节点分布Fig.3 Distribution of each node

表1 各节点间的OD运输量

参数设置:我们设置3种不同经济规模折扣系数的场景，分别是α=0.2，α=0.5，α=0.8，为了分析枢纽节点数量限制对结果的影响，给出p=(3,4)场景下的轴辐式网络节点分配图；同时分析不同拥堵成本参数组合场景下对轴辐式网络设计的影响，分别给出拥堵成本函数参数a,b，分别选取a=(0.1，1，10)；b=(1，1.1，1.5，2.0)；

下面是随着限制枢纽个数、拥堵成本参数变化的情况节点指派关系图。其中图4(a)为限制枢纽个数为3个，且α=0.2，a=10，b=1.5情况下节点指派关系图；图4(b)为限制枢纽个数为3个，且α=0.2，a=10，b=2.0情况下节点指派关系图。

图4 限制枢纽数量为3个的节点指派关系Fig.4 Assignment relationship when the limit of the number of hubs is 3

3.2 结果分析

为检验模型对Hub网络拥堵的控制效果，我们引入了货流量不平衡比以体现设计模型的目的是分散货流量、缓解干线运输拥堵和枢纽之间规模经济效应的矛盾来使总成本最小。

为了分析限制枢纽数量p对轴辐式网络优化结果的影响，我们分析了当p=3和p=4情景下的货流量不平衡比和网络总成本的对比情况，分析结果如表2。

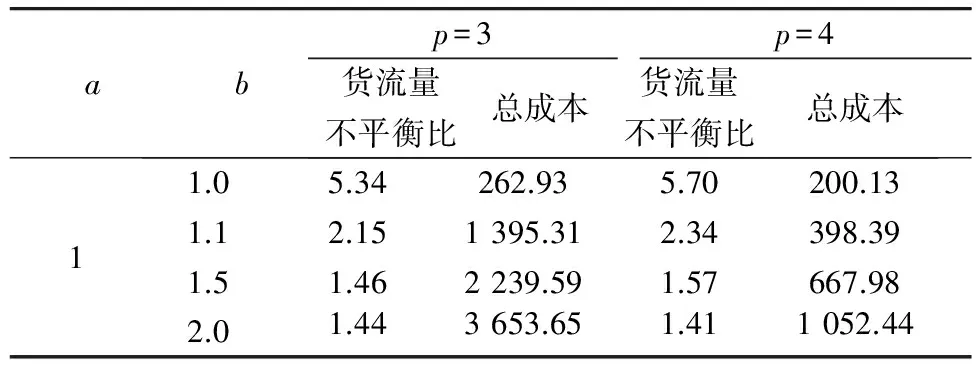
表2 不同限制枢纽数量p对不平衡比和总成本的影响

为了分析规模经济折扣系数α对结果的影响，我们分析了在限制枢纽数量p=3、不同α情景下枢纽节点选择、总成本和货流量不平衡比的变化情况，对比分析结果如表3。

表3 不同经济规模折扣系数α下的对比分析结果

表4是在经济规模折扣系数α=0.5，拥堵成本参数a=1和枢纽节点个数p=3的情况下，比较分析不考虑Hub网络拥堵和考虑拥堵下的枢纽节点货流量分配和货流量不平衡比。这体现考虑Hub网络拥堵对轴辐式网络优化的重要性。

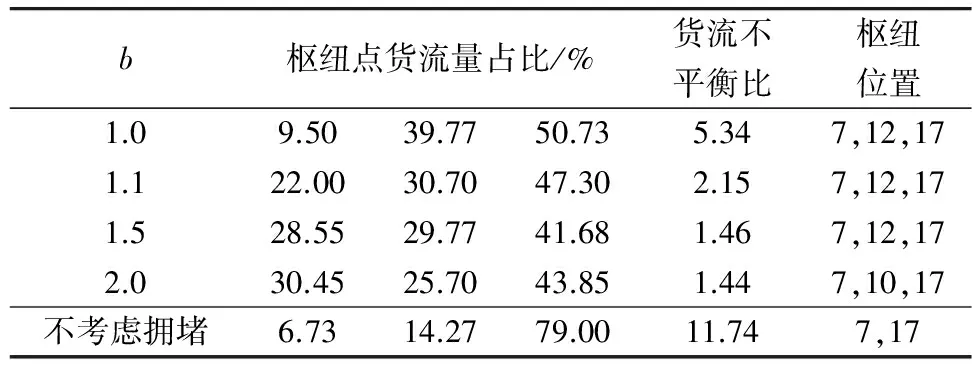
表4 考虑Hub网络拥堵和不考虑拥堵情况下的流量分配和不平衡比

通过对表2～表4的数据分析可以得出以下结论：

1)限制枢纽数量p对结果的影响。在保持拥堵成本参数a和b不变的前提下，有更多的枢纽节点选择的网络总是有着更低的总成本。这是因为：一方面是更多的枢纽节点意味着Hub网络上枢纽之间可以利用更多的经济规模效应，从而降低总成本；另一方面是更多的枢纽节点意味着辐节点能够找到更好的路线，减少运输距离、降低运输时间，从而在保证Hub网络经济规模效应的同时减少Hub网络拥堵成本。

2)从表3可以看出随着枢纽节点个数限制和拥堵成本参数的变化时，有一些节点总是被选择成为枢纽节点，例如表格中的枢纽节点7。可能原因是节点的地理位置处于整个轴辐式网络的中间地带，这样可以包含周围更多的辐节点，以此减少运输距离和更加容易达到经济规模效应，降低总成本。

3)经济规模折扣系数α对结果的影响。随着经济规模折扣系数的逐渐增大，不同拥堵成本参数下的总成本也逐渐增加。这是因为α的增大，Hub网络的经济规模效应减少，但Hub网络的拥堵成本却逐渐增加。同时α的变化对结果的影响也体现在货流量不平衡比上。最大的不平衡比出现在α取 0.2 时，达到了6.47；最小的不平衡比出现在α取 0.8 时，比值为1.12。通过观察各表中纵向数值的变化规律，可以认为α越小则货流量不平衡比越大。这样的结果符合为了追求经济规模效应而把货流量集中于某些关键枢纽节点网络之上的客观情况。反之，如果α越大，即规模效益不显著，则对应的不平衡比就越小，说明追求经济规模效应会使Hub网络拥堵越严重，对控制Hub网络拥堵起到反作用。

4)Hub网络拥堵是轴辐式网络优化的重要因素之一。从表4可以看出，在不考虑拥堵情况下货流量不平衡比最大，比值为11.74。这是因为为了追求轴辐式网络的经济规模效应来降低总成本，使货流量都集中在某一关键枢纽节点上，然后通过此枢纽节点运输到目的地。但每个枢纽节点的能力水平有限，这样势必造成Hub网络严重拥堵反而大量地增加总成本。而考虑Hub网络拥堵的模型能够更好的平衡枢纽节点流量，这样可以平衡经济规模效应与Hub网络拥堵的矛盾，从而使总成本最小，也符合现实生活中的实际情况。

5)拥堵成本参数a和b对结果的影响。从表2～表4可以看出枢纽节点的选择和货流量不平衡比随拥堵成本参数a和b变化而变化。其中参数b代表非线性拥堵成本的水平，随着b的增大，总成本逐渐增加，而货流量不平衡比逐渐减少，这是因为由于拥堵成本的增加，货流量会分配到其他枢纽节点来缓解Hub网络拥堵，这说明拥堵成本函数对Hub网络货流量的分配起到了关键的作用。而当b=2.0时，最佳枢纽由7节点代替了原来的12节点，可能原因是Hub网络拥堵程度完全超过7节点的能力水平，对平衡经济规模效应和Hub网络拥堵起反作用，增加了总成本，就需要选择能力水平更高的枢纽节点来控制Hub网络拥堵。

4 结 语

在轴辐式网络背景下，枢纽节点通过集散货物，产生hub网络经济规模效应来降低成本。但这样就会造成干线运输上的拥堵，为此也会增加总成本。枢纽节点之间的拥堵对整个轴辐式网络造成严重的经济损失，已成为轴辐式网络优化的一大难题。针对轴辐式网络的干线运输的规模经济效应与拥堵矛盾问题，建立了基于干线运输拥堵成本的混合整数非线性模型，在保证轴辐式网络节点正常运输的前提下，通过确定枢纽节点和辐节点及流量分配，最大限度的平衡货物运输使总成本最小化。这对未来轴辐式网络优化中考虑干线运输拥堵具有重要的参考价值。后续研究可从以下几个方面进行：在考虑拥堵成本的同时考虑枢纽节点的容量限制的轴辐式网络优化，这样更加符合实际情况；将单分配模式改成多分配或者将规模经济系数改写为节点货量的函数以更好地体现规模经济效应。有关拥堵成本函数的参数的设定有待商榷，对于拥堵成本函数的研究未来仍将继续深入。

[1] O’ KELLY M E.A quadratic integer program for the location of interacting hub facilities [J].EuropeanJournalofOperationalResearch,1987,32(3):393-404.

[2] O’KELLY M E.Rectilinear minimax hub location problems [J].JournalofGeographicalSystems,2009,11(3):227-241.

[4] MEYER T,ERNST A T,KRISHNAMOORTHY M.A 2-phase algorithm for solving the single allocation-hub center problem [J].Computers&OperationsResearch,2009,36(12):3143-3151.

[5] LIN C C.The integrated secondary route network design model in the hierarchical hub-and-spoke network for dual express services [J].InternationalJournalofProductionEconomics,2010,123(1):20-30.

[6] ALUMUR S A,KARA B Y,KARASAN O E.Multimodal hub location and hub network design [J].Omega,2012,40(6):927-939.

[7] 陆化普,蔚欣欣,卞长志.OD 需求不确定的离散交通网络设计模型研究[J].公路交通科技,2011,28(5):128-132. LU Huapu,YU Xinxin,BIAN Changzhi.Model and algorithm of discrete network design problem under OD demand uncertainty [J].JournalofHighwayandTransportationResearchandDevelopment,2011,28(5):128-132.

[8] 翁克瑞,杨超.顺应潮流的轴辐式物流网络[J].物流技术,2006 (7):14-16. WENG Kerui,YANG Chao.On Hub-and-spoke logistics networks [J].LogisticsTechnology,2006(7):14-16.

[9] 翁克瑞.带固定轴线成本的轴辐式网络设计问题[J].运筹学学报,2012,16(1):88-96. WENG Kerui.The stability of the solutions of optimization hub and spoke network design problem with fixed hub arc costs [J].OperationsResearchTransactions,2012,16(1):88-96.

[10] 郭建华.主成分分析法在区域轴-辐式快运网络枢纽节点城市布局中的应用研究[J].公路交通科技(应用技术版),2009(3):178-181. GUO Jianhua.Applied research spoke express network hub nodes urban layout - principal component analysis in the area of the shaft [J].JournalofHighwayandTransportationResearchandDevelopment(ApplicationTechnologyEdition),2009(3):178-181.

[11] 崔小燕,李旭宏,毛海军,等.无容量约束单分配轴-辐式物流网络设计[J].交通运输系统工程与信息,2010,10(5):175-181. CUI Xiaoyan,LI Xuhong,MAO Haijun,et al.Design of uncapacitated hub-and-spoke logistics networks with single allocation [J].JournalofTransportationSystemsEngineeringandInformationTechnology,2010,10(5):175-181.

[12] 陈淑文.港口拥堵难题危及全球海运系统[J].中国远洋航务,2007(3):24-25. CHEN Shuwen.Port congestion problems threatening the global maritime system [J].MaritimeChina,2007(3):24-25.

[13] 寿建敏.港口拥堵催生多式联运和世界海运格局的变化[J].集装箱化,2005(9):41-43. SHOU Jianmin.Intermodal and port congestion spawned change the pattern of world seaborne [J].Containerization,2005(9):41-43.

[14] LEACHMAN R C,PAYMAN J.Congestion analysis of waterborne containerized imports from Asia to the United States [J].TransportationResearchPartE,2011,47(6):992-1004..

[15] FAN L,WILSON W W,DAHL B.Congestion,port expansion and spatial competition for US container imports [J].TransportationResearchPartE,2012,48(6):1121-1136.

[16] KIM K H,KIM K Y.An optimal routing algorithm for a transfer crane in port container terminals [J].TransportationScience,1999,33(1):17-33.

[17] GUO X,HUANG S Y.Dynamic space and time partitioning for yard crane workload management in container terminals [J].TransportationScience,2012,46(1):134-148.

[18] CHOO S,KLABJAN D,SIMCHI-LEVI D.Multiship crane sequencing with yard congestion constraints [J].TransportationScience,2010,44(1):98-115.

[19] CHEN G,GOVINDAN K,YANG Z Z.Managing truck arrivals with time windows to alleviate gate congestion at container terminals [J].InternationalJournalofProductionEconomics,2013,141(1):179-188.

[20] 林天倚.考虑拥堵与环境成本的轴辐式集装箱海运网络枢纽港选择[D].上海:上海交通大学,2013. LIN Tianyi.HubLocationProblemofHub-and-SpokeNetworkofLinerShippingServicewithCongestionandEnvironmentalCost[D].Shanghai:Shanghai Jiaotong University,2013.

[21] GROVE P G,O’KELLY M E.Hub networks and simulated schedule delay [J].PapersinRegionalScience,1986,59(1):103-119.

[22] GILLEN D,LEVINSON D.Full cost of air travel in the California corridor [J].TransportationResearchRecord:JournaloftheTransportationResearchBoard,1999,1662(1):1-9.

Hub and Spoke Network Optimization Based on Hub Network Congestion

YANG Bin, DENG Zhihui, HU Zhihua

(Logistics Research Center, Shanghai Maritime University, Shanghai 201306, P.R.China)

In the background of hub and spoke network, hub nodes generated the scale of economic effect to reduce costs by distribution cargo. Meanwhile, it would increase the likelihood of costs increase and Hub network congestion. Firstly, in order to ease the Hub network congestion and reduce its cost of economic loss, the congestion cost function associated with the node flow in the Hub and spoke network was proposed. Secondly, under the premise of ensuring the normal cargo transportation of the axis and radial network nodes, the balance between the economic effect caused by the scale of goods transport and the caused hub network congestion costs was maximized, and the mixed-integer nonlinear programming model was established to minimize transportation costs, construction costs and congestion costs. Finally, a case study was carried out to verify the influence of Hub network congestion on network optimization and the reasonableness of model, which had important reference value for balancing the scale economic effect and the Hub and spoke network optimization of Hub network congestion in the future.

traffic and transportation engineering; Hub and Spoke network; network optimization; Hub site; Hub network congestion; mixed-integer nonlinear

2014-08-15；

2014-11-08

国家自然科学基金项目(71171129)；上海市科委科研计划项目( 12510501600，11510501900，12dz1124802，14DZ2280200)

杨 斌(1975—)，男，山东青岛人，教授，博士，主要从事绿色物流等方面的研究。E-mail：binyang@shmtu.edu.cn。

10.3969/j.issn.1674-0696.2016.01.27

U492.3+32

A

1674-0696(2016)01-138-07