基于悬索桥主缆热物性参数试验的温度场研究
2016-05-25伟张亮亮钟
张 伟张亮亮钟 宁
(1. 重庆大学 土木工程学院, 重庆 400045;2. 重庆高速公路集团有限公司,重庆 401121)
基于悬索桥主缆热物性参数试验的温度场研究
张 伟1, 2,张亮亮1,钟 宁2
(1. 重庆大学 土木工程学院, 重庆 400045;2. 重庆高速公路集团有限公司,重庆 401121)
推导了主缆结构在芯部加热作用下温度场的稳态与瞬态解析解,采用与实际桥梁相同的试验模型,测试得到了主缆结构的表观热扩散系数与表观导热系数。在采用测试参数的基础上,通过对桥梁主缆温度场的有限元计算及与实桥主缆温度场实测结果的对比,证明了计算方法的精确和可靠,可用于悬索桥主缆设计、施工和运营阶段的温度场计算。
桥梁工程;主缆;热扩散系数;导热系数;非稳态;热传导
0 引 言
鱼嘴长江大桥全长1 438 m,桥梁布置为(12×35 +616 +7×56) m,主桥为616 m单跨双立铰简支悬索桥,是重庆及西南地区同类型桥梁中跨度最大的桥梁。上部结构主缆共2根,每根长度为1 098.4 m,主缆采用预制平行钢丝索股,每根主缆为65股,每股由127根平行镀锌高强钢丝组成,排列成近似正六边形。主缆钢丝采用φ5.20 mm,钢丝强度为1 670 Mpa。主缆外径分别为519 mm(索夹处)、525 mm(索夹外),主缆截面布置见图1。
大桥南岸为崖面,北岸为滩地,两岸环境条件差异很大,不均匀的日照和夜间散热,导致主缆温度场分布不仅沿索长和横桥向分布不均匀,主缆断面内温度也极不均匀,主缆温度场分布不对称且复杂。主缆的线形控制是鱼嘴长江大桥悬索桥施工控制的关键[1],虽然索股架设调整时都是在夜间温度稳定时进行,但是大量的实测数据表明,由于散热的边界条件不同,各索股之间的温度仍然会存在一定差别[2]。这种差别如果没有考虑,将会导致索股线形偏差,给紧缆带来较大困难,并会使成桥阶段索股之间有一定的拉力差,不利于主缆受力。
1 系数测试原理
根据主缆的受热特性,可将主缆温度场的变化视为热传导问题,按照傅里叶定律,柱坐标下的主缆非稳态热传导微分方程为:
(1)
式中:t为温度;τ为时间;λ为导热系数;ρ为材料密度;c为材料比热容。

图1 鱼嘴长江大桥主缆截面Fig.1 Cross-section of main cable of Yuzui Yangtze River Bridge
根据传热学理论可知,当需要确定悬索桥主缆或任何实际结构温度场时,前提条件是需要首先掌握实际结构的表观热物性参数,即采用国外的研究成果或通过模型试验的方法测定主缆各种状况下的表观热物性参数,然后根据边界条件,求解主缆热传导非稳态微分方程或采用数值分析的方法计算主缆的有限元模型[3]。
假定主缆材料为匀质各向同性材料,截面半径为r0。考虑到主缆沿轴向很长, 该情况可以看成沿半径方向的一维瞬态轴对称问题,假设热扩散系数a为常数,环境空气温度为T∞。令θ=T(r,t)-T∞该定解问题的数学表达式为:
τ=0,θ(r,0)=θ0=T0-T∞;
(2)
式中:a=λ/ρc,λ为主缆表观导热系数,ρ为主缆的等效密度,c为主缆的比热;q为单位长度加热功率;rg为加热管半径;r0为主缆半径,h为主缆表面对流换热系数。
根据传热学理论,定义毕奥数和傅里叶数为:
当F0>0.2以后,上式的解析解可以归纳如式(3)。
(3)
式(3)中前两项为稳态解,第3项为瞬态解。瞬态反应中,主缆中过余温度的对数值与时间成线性关系,将式(3)移项,对两边取对数,再对时间求导,得:
(4)
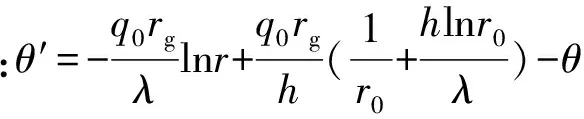
当F0≥0.2以后,物体中任意一点的温度与时间的关系,在半对数坐标上为一组彼此平行的直线,其斜率为m1,即m1只与温升速率有关。
从式(4)可知,通过直接测定主缆中温度的变化率,就可以换算得到主缆的热物参数。m1可以通过试验测试不同时间的温度得到,即:
(5)
于是待测物料的热扩散系数α可由式(6)获得,即:
(6)
μ1下式(7)的超越方程根的第1个根。
(7)
2 试验测试
为了对比和验证,主缆试验模型采用两种,缩小模型直径0.38 m和实际桥梁主缆的直径0.525 m。主缆空隙率分别为19.5%和17.1%。试验模型见图2。模型长度为2 200 mm,在主缆截面布置温度传感器测点,采用计算机自动采集温度数据。主缆的两端采用聚氨酯泡沫覆盖,以阻止端部热量损失[4]。采用PT100铂电阻温度传感器测试截面温度,该温度传感器性能稳定,精度和线性度较其他类型的要好。试验时采用220 V/110 V的高精度稳压电源。

图2 主缆试验模型Fig.2 Test model for main cable
2.1 稳态测试
本试验测试的是主缆整个截面的平均导热系数。试验一共设计了3个工况,其中模型1设计了2个工况(工况1:加热功率248 W;工况2:加热功率992 W);模型2设计了1个工况(工况3:加热功率500 W)。图3给出工况1下实测“温度-时间”曲线。

图3 工况1测点温度-时间曲线Fig.3 Temperature-time curve of measuing point in case 1
每种工况下的试验均测试了两次,试验测试结果见表1。可见各种工况计算得到的导热系数吻合较好。主缆在室温下加热测试得到的平均导热系数为1.2 W/(m·℃),一般钢材的导热系数在50 W/(m·℃)左右,可见主缆表观导热系数约为钢丝导热系数的1/40。比较工况1和工况2计算结果发现,两次计算结果差别很小,在3%以下,可认为主缆的温度对导热系数的影响很小,可以忽略不计。
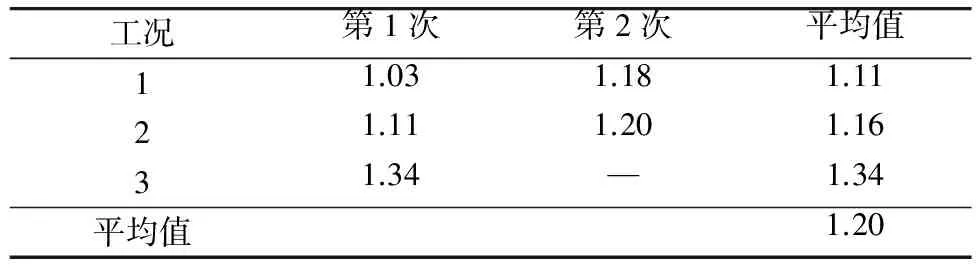
表1 表观导热系数测试结果
2.2 瞬态测试
瞬态测试方法的关键是温度数据的采集需要快速准确,保证采集到温度的变化率[5]。试验分为3个工况,工况1:加热功率248 W;工况2:加热功率992 W;工况3:加热功率500 W。试验测试的基本参数见表2。
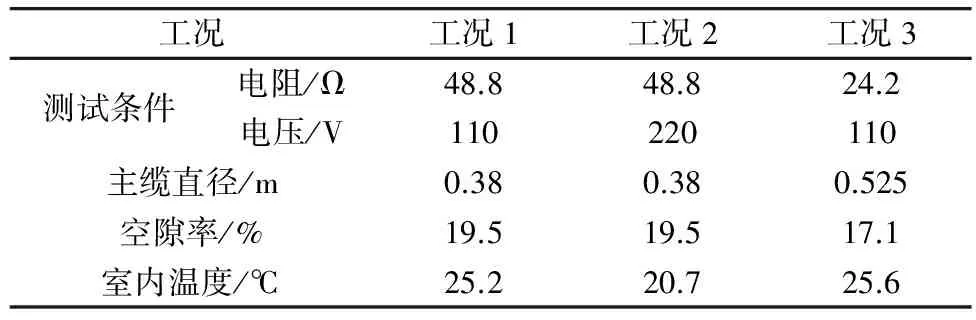
表2 试验测试基本参数
试验时,通过测试温度-时间曲线,当曲线斜率基本保持常数的时段为主缆系统达到准稳态的标准,工况1试验测试的主缆中部截面温度测点的温度随时间的变化见图4。由式(7)计算得到的工况1的斜率如图5。计算得到的直线斜率(-m)在工况1和工况2下均为-1.0×10-5,在工况3下计算斜率为-6.0×10﹣6。

图4 工况1中部测点温度-时间曲线Fig.4 Temperature-time curve of central measuring point in case 1
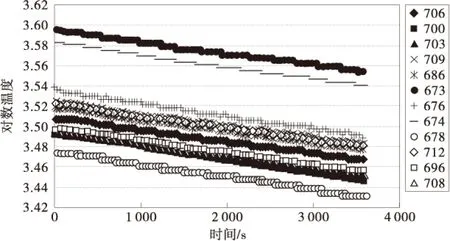
图5 工况1时间-对数温度曲线Fig.5 Time-logarithmic temperature curve of case 1
由前节理论和试验测试数据,采用数值方法计算μ值,计算各个工况的相关参数及热扩散系数如表3。
表3 计算各工况Bi,μ1,α
Table 3 Calculation ofBi,μ1andαin various cases

项目工况1工况2工况3Bi0.4970.4970.687μ10.940.941.1斜率m1.0×10-51.0×10-56.0×10-6热扩散系数α/(m2·s-1)4.0×10-74.0×10-73.48×10-7
经验算,在各工况的试验测试时,计算得傅立叶数F0=at/R2>0.2;故满足计算条件。综合两种模型3个工况,主缆在室温下加热测试得到截面平均热扩散系数为:3.74×10-7m2/s。
3 主缆传热学有限元计算模型
3.1 稳态验证
对实际测试得到数据进行计算验证[6],考虑主缆达到稳态的情况,取主缆截面为0.38 m的圆,主缆的实测平均热传导系数1.11 W/(m·℃),主缆中心加热功率248 W(112.7 W/m);边界采用第一类边界条件,即用实测的主缆外表面温度值计算。
主缆单元采用温度单元plane55[7]。实际计算结果如图6,温度实际测试值和计算值对比见表4。

图6 主缆计算结果Fig.6 Calculation results of main cable

表4 截面温度计算值与实测值对比
3.2 瞬态验证
对实际测试得到的数据进行计算验证,由模型试验得到的表观热扩散系数和主缆表面表观换热系数,计算主缆在瞬态情况下的温度场[8]。主缆与外界环境进行对流换热,忽略主缆对外热辐射散热,计算用试验实测的主缆表面换热系数,这样既可以验证表观热扩散系数是否准确可信,也验证了表面换热系数的准确性[9]。主缆计算模型采用温度单元plane55建模,计算基本参数和边界条件为:直径0.38 m;空隙率19.5%;环境温度20.7 ℃;温度变化等级9.1 ℃, 温度变化等级取瞬态计算的时段开始和结束时截面平均温度的差值;截面初始温度30 ℃; 等效比热508 J/(kg·K);等效密度6 320 kg/m3。主缆中心加热功率为451 W/m。
实际计算结果如图7,温度实际测试值和计算值对比见表5。
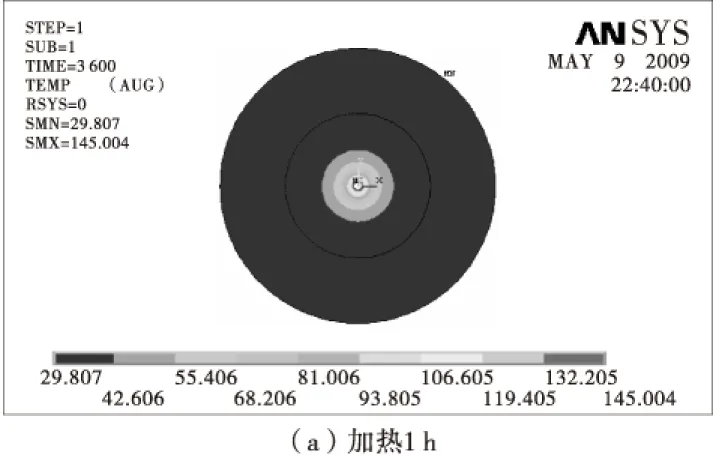
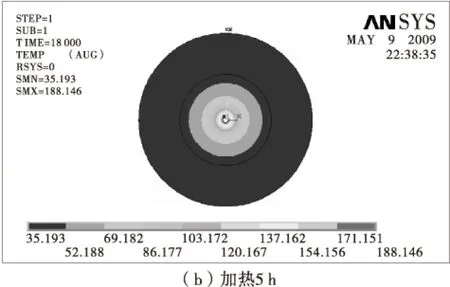

图7 温度场分布Fig.7 Temperature field distribution

表5 实测值及仿真分析结果对比
由表5可见,计算结果比实测值小,最大误差基本在10%以下。考虑到瞬态测试误差和计算误差,存在的误差在容许的范围内。该计算也同时验证了试验测试的自然对流条件下的换热系数的准确性。
综上所述,可见实测模型测点温度与仿真计算模型测点温度很接近,说明用实测得到的主缆模型热物性参数进行稳态下的主缆模型温度场仿真计算,结果能够反映实际结构的温度分布。
4 结 论
依托鱼嘴长江大桥,通过主缆模型的一系列试验测试,遵循传热学理论和实验传热学方法,计算得到主缆复合材料在室温下的热扩散参数、平均表观热扩散系数并对实际测试得到的数据进行计算验证。
1)主缆截面温度场计算值与实测结果对比表明,试验测试和计算方法可靠,具有足够的计算精度。
2)通过在计算模型中引入给定的边界条件和初始条件,能够得到主缆在特定环境条件下的温度场,该理论和方法可以用于悬索桥主缆设计、施工和运营阶段的温度场计算。
3)分析试验测试结果和理论计算,总结影响因素有主要以下两个方面:主缆结构的影响,主缆结构对热物性参数的影响主要表现在主缆的空隙率大小,以及主缆本身结构的均匀性上随着空隙率的减小,导热系数变大而热扩散系数有所变小;温度对热物性参数的影响,主缆截面的温度场与导热系数,主缆表观比热,密度以及表面换热系数相关,其中,主缆的比热容和导热系数对温度场的影响最大。
[1] 范立础,潘永仁,杜国华.大跨度悬索桥结构架设参数精细算法研究[J].土木工程学报,1999,32(6):20-25. FAN Lichu,PAN Yongren,DU Guohua.Research on long-span suspension bridge erected fine algorithm parameters [J].ChinaCivilEngineeringJournal,1999,32 (6):20-25.
[2] 潘永仁,范立础.悬索桥施工中主缆横截面平均温度实用计算法[J].同济大学学报(自然科学版),1998,26(2):114-119. PAN Yongren,FAN Lichu.The calculation method of suspension bridge main cable section in practical average temperature [J].JournalofTongjiUniversity(NaturalScience),1998,26(2):114-119.
[3] 张永水,罗红,王祖华.温度对悬索桥空缆线形的影响分析[J].重庆交通学院学报, 2005,24(6):21-24. ZHANG Yongshui,LUO Hong,WANG Zuhua.The analysis of temperature influence on empty shape of suspension bridge [J].JournalofChongqingJiaotongUniversity,2005,24(6):21-24.
[4] 张加晚.阳逻长江大桥温度场测试及主缆温度效应研究 [D].武汉:华中科技大学,2007. ZHANG Jiawan.ResearchonTemperatureFieldTestsWITYangtzeRiverBridgeandtheMainCableTemperatureEffects[D].Wuhan:Huazhong University of Science and Technology,2007.
[5] 白剑.悬索桥施工过程温度场测试及温度效应分析[D].西安:长安大学,2004. BAI Jian.SuspensionBridgeConstructionProcessTemperatureFieldTtestingandAnalysisofTemperatureEffect[D].Xi’an:Chang’an University,2004.
[6] ZELENTSOV Y A,ZELENTSOV V Y.An investigation of the relation between the temperature dependences of the initial unbalance and the output signal of resistance strain sensor bridge circuits [J].MeasurementTechniques,2007,50 (1):66-68
[7] 张国智,胡仁喜,陈继刚,等.ANSYS10.0热力学有限元分析实例指导教程[M].北京:机械工业出版社,2007. ZHANG Guozhi,HU Renxi,CHEN Jigang,et al.ExamplesoftheRmodynamicANSYS10.0FiniteElementAnalysisTutorial[M].Beijing:Mechanical Industry Press,2007.
[8] 林一宁,余屏孙,林亚超.悬索桥架设期间主缆温度测试研究[J].桥梁建设,1997(3):58-66. LIN Yi’ning,YU Pingsun,LIN Yachao.Testing of the main cable temperature during Suspension bridge erection [J].BridgeConstruction,1997(3):58-66.
[9] 王润富,陈国荣.温度场和温度应力[M].北京:科学出版社,2005. WANG Runfu,CHEN Guorong.TemperatureFieldandThermalStress[M].Beijing:Science Press,2005.
Temperature Field Research Based on Main Cable ThermalParameters of Suspension Bridge
ZHANG Wei1, 2, ZHANG Liangliang1, ZHONG Ning2
(1. School of Civil Engineering, Chongqing University, Chongqing 400045, P.R.China;2. Chongqing Expressway Group Co.,Ltd., Chongqing 401121, P.R.China)
The temperature field steady and transient analytical solutions of the main cable structure in heating of the core were deduced. The same test model with the actual bridge tested was used, and the apparent thermal diffusivity coefficient and thermal conductivity coefficient of the main cable structure were obtained. Based on the use of the test parameters, the proposed calculation method was proved to be accurate and reliable, which could be used for the temperature field calculation of the main cable of suspension bridge in design, construction and operational phase, by the the finite element calculation of temperature field of the bridge main cable and its comparison with the measured results of the real bridge main cable temperature field.
bridge engineering; main cable; thermal diffusivity coefficient; thermal conductivity coefficient; non-steady state; heat conduction
2014-03-19;
2014-09-23
张 伟(1978—),男,山东枣庄人,高级工程师,博士研究生,主要从事桥梁施工管理方面的研究。E-mail:19509256@qq.com。
10.3969/j.issn.1674-0696.2016.01.01
U448.25
A
1674-0696(2016)01-001-04
