基于不同拱脚形式下抗滑桩土拱效应研究

任永忠，马守才

(兰州工业学院 土木工程学院，甘肃 兰州 730050)

基于不同拱脚形式下抗滑桩土拱效应研究

任永忠，马守才

(兰州工业学院 土木工程学院，甘肃 兰州 730050)

目前针对抗滑桩桩间土拱拱脚形式的研究基本为桩身、桩侧摩阻力和两者同时参与(联合)3种形式。为了研究3种拱脚形式下土拱的受力机理及影响因素，采用土工有限元Plaxis V8.5对其进行数值研究，在研究过程中3种形式拱脚采用分别建模，为了体现桩侧与土体的摩擦特性，采用软件提供的界面单元来模拟。研究表明：悬臂式抗滑桩土拱的拱脚支撑力主要由桩身来提供，桩侧提供的支撑力有限；随着桩间距的增加，土拱不易形成，以桩身为拱脚的法向应力在以联合为拱脚的法向应力中所占比例逐渐减小。

岩土工程；抗滑桩；土拱效应；拱脚；桩间距；数值分析

0 引 言

在抗滑桩设计中桩间距的确定直接决定了其支挡的成败与否，抗滑桩桩间距过大，在滑坡推力作用下滑坡土体从桩间被挤出，起不到抗滑桩的支挡效果；反之，抗滑桩间距过小，造成不必要的工程浪费，为此许多学者针对合理桩间距进行了较为系统全面的分析研究。首先K.TERZAGHI[1]通过砂土的活动门试验验证了土力学领域中土拱效应的存在。D.L.WANG等[2]将土拱效应引入抗滑桩桩间距的确定中并提出了极限桩间距的存在。从此抗滑桩桩间距的确定多数采用土拱效应理论进行研究。文献[3-4]以桩侧摩阻力承担桩间滑坡土体的全部滑坡推力，并基于土拱静力平衡提出了最大桩间距的估算模型。王士川等[5]考虑土拱作用及桩断面间土体的摩阻力及黏着力的前提下对桩间块体进行稳定分析，在抗滑桩桩间距的上限解的基础上提出了下限解。周德培等[6-7]以桩身为土拱的拱脚，同时结合拱脚和跨中土体的强度破坏准则推导了桩间距的表达式。同时针对土拱的形成力学过程，分别从力学机制，引入数学分析方法和普氏理论等对土拱的拱轴线和桩间距进行了分析研究[8-11]。为了进一步分析研究，文献[12-14]分别采用室内离心试验、现场足尺试验的方法对桩间土体形成土拱的过程进行了详细的研究。由于试验不能研究土拱形成过程应力的变化，因此许多学者采用有限元或者颗粒流软件对其进行了深入的分析[15-21]。从以上文献的分析可以看出，均是在土拱拱脚假定为桩身或者桩身侧面摩阻力基础上研究其形成过程中桩身内力或应力的变化等要素，但是由文献[14]引用的工程实例来看，土拱的拱脚并非是桩身或桩侧摩阻力单独来参与，而是两者共同承担。为此笔者采用数值分析的方法对拱脚3种不同形式下的土拱进行深入地研究。

1 计算理论

1.1 桩身为拱脚时的土拱效应及桩间距

在滑坡推力作用下，抗滑桩以及桩间土均要发生横向位移，但是抗滑桩横向位移小于桩间土的横向位移，随着横向位移逐步增大，桩间土产生不同程度的剥落，距离抗滑桩较远的位置剥落深度较大，抗滑桩附近剥落深度较小，形成拱形的剥落曲线，在剥落过程中由于桩间土和抗滑桩之间横向位移不相等，最后形成土拱拱圈。文献[6]认为桩身为土拱的拱脚以限制桩间土体的横向位移发展。桩身为拱脚时土拱受力图见图1。

图1 桩身为拱脚时土拱受力Fig.1 Force diagram of taking pile body as skewback

为此假定文献[6]不考虑土拱内侧土体的抗滑力以及土拱拱圈的自重，同时认为桩后滑坡推力沿土拱长度方向是均匀分布的，建立了相应的计算模型。

土拱破坏强度条件为：

1)两桩侧面的摩阻力之和不小于桩间作用于土拱上的压力：

2(Fxtanφ+ct)=ql

(1)

式中：Fx为土拱破坏截面上水平分力；c，φ为滑坡土体的黏聚力和内摩擦角；t为土拱拱圈厚度；q为单位土层厚度的滑坡推力；l为桩间净距。

2)土拱跨中前缘土体M点的强度条件，基于Mohr-Colomb强度准则建立：

(2)

式中：参数物理意义同前。

3)土拱拱脚受压区土体不被破坏，因此须满足Mohr-Colomb强度准则：

Tcos(α+β)=ct+Tsin(α+β)tanφ

(3)

式中：T为土拱拱脚破裂面上的合力；α为土拱拱脚破裂面与水平方向的夹角；β为土拱拱脚破裂面上合力与水平方向的夹角；其他参数同前。

通过式(1)～式(3)联立求解可得：

(4)

式中：b为抗滑桩截面宽度，其他参数同前。

1.2 桩侧摩阻力为拱脚时的土拱效应及桩间距

桩侧摩阻力为拱脚时认为滑坡推力均传至抗滑桩两侧面上，由桩间土与桩侧面之间的摩擦阻力来提供平衡滑坡推力，为此基于以上的分析，文献[3]认为土拱的拱脚由桩侧面摩阻力来提供。桩侧摩阻力为拱脚时土拱受力见图2。

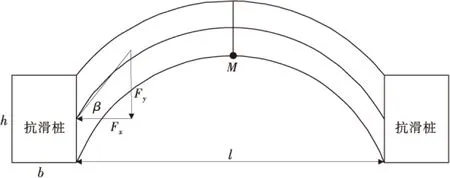
图2 桩侧摩阻力为拱脚时土拱受力Fig.2 Force diagram of taking side friction of pile as skewback

土拱破坏控制条件为：

1)桩侧面的摩阻力不小于作用在土拱上的单位厚度滑坡土体的推力：

2(Fxtanφ′+c′h)=ql

(5)

式中：c′，φ′为滑坡土体与桩侧面的黏聚力和内摩擦角；h为抗滑桩截面的高度；q为单位厚度滑坡土体的推力；l为抗滑桩净距。

2)土拱跨中前缘M点为单向受力状态，在土拱传力过程中为不利点，为此依据Mohr-Colomb强度准则建立方程：

(6)

式中：c，φ为滑坡土体的黏聚力和内摩擦角；β为土拱拱脚破裂面上合力与水平方向的夹角。

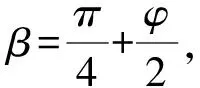
(7)

桩间净距式(7)为在不同的控制条件下而得，为此为保证土拱不被破坏，最终的桩间净距为l1和l2的最小值。

2 数值分析研究

采用Plaxis2D V8.5岩土分析有限元软件。土体本构关系采用Mohr-Coulomb，针对模型的选取，依据以往许多学者建立模型的尺寸而选定，桩采用矩形截面，截面尺寸b×h为1.5 m×2.0 m，l为桩的净距。模型尺寸依据研究问题的不同进行调整，但是研究区域距离荷载施加边界处假定为10h。在模型的上部施加均布荷载来模拟滑坡推力的作用。在此分析中最为关键的步骤为桩身或桩侧面为拱脚的模拟，为此通过设置板单元和约束相应方向的位移来实现，为了考虑滑坡土体与桩侧面摩擦特性，在板单元与土体之间设置界面单元，其界面强度因子Rinter=0.7。模型计算参数见表1，有限元计算模型见图3。

表1 模型计算参数

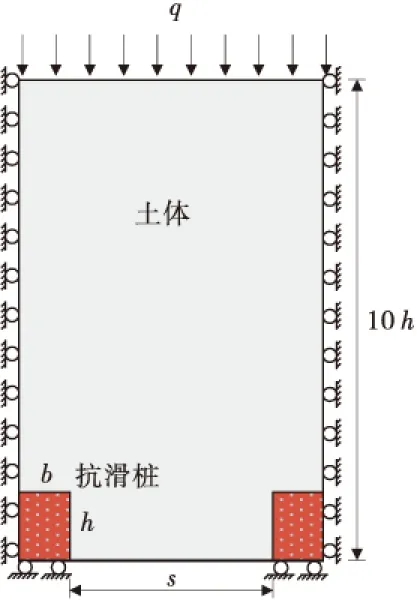
图3 计算模型Fig.3 Calculation model

为了研究不同拱脚形式下桩间土体形成土拱的过程，将桩分为不同形式，联合拱脚时直接采用模型桩考虑，桩侧摩阻力为拱脚时采用软件中提供的板单元，这是为了考虑桩间土与桩侧界面特性，桩身为拱脚时同样采用板单元，与桩侧为拱脚不同的是界面强度折减因子不同而已。

图4为不同拱脚形式下主应力拱的示意图。从图中可以看出，联合和桩身为拱脚时桩后土体形成了明显的主应力，而桩侧摩阻力为拱脚时主应力拱不是很明显。由此可知桩后主应力拱的形成主要靠桩身背侧的支挡作用而形成，桩侧摩阻力所参与形成的土拱占的比例很少，针对所占的比例不能一概而论，因为影响因素诸多。同时由实际工程可知，由于在自重作用下桩间土发生滑塌现象，因此以桩侧摩阻力为拱脚所形成的土拱就会更小。

图4 不同拱脚形式下主应力拱示意Fig.4 Schematic of principal stress of soil arching with the different forms of skewback

3 数值结果分析

3.1 应力分量σy分布曲线

在联合、桩身和桩侧不同的拱脚形式下桩间土在y方向上0，1，3，5，7 m主应力曲线如图5。

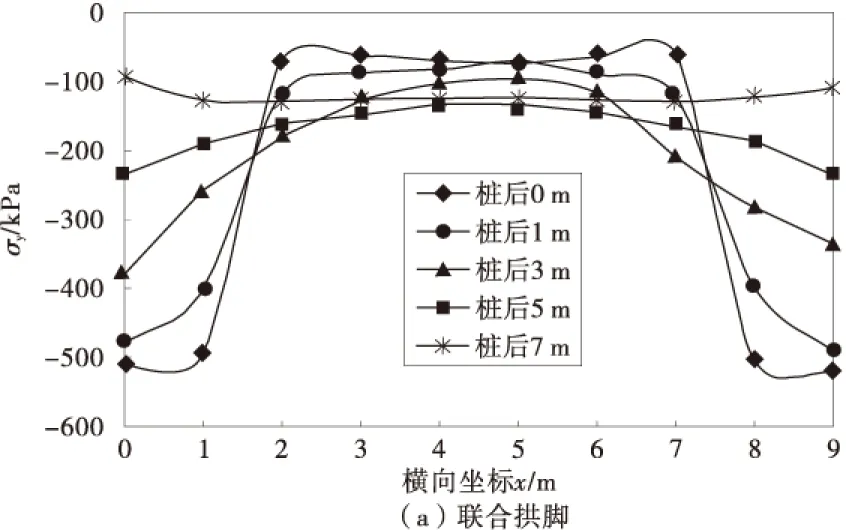
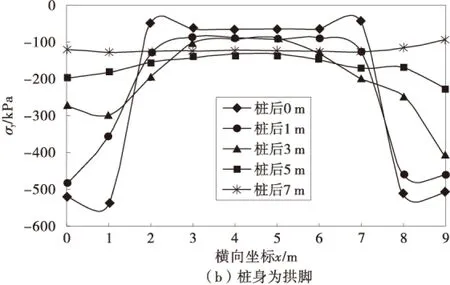
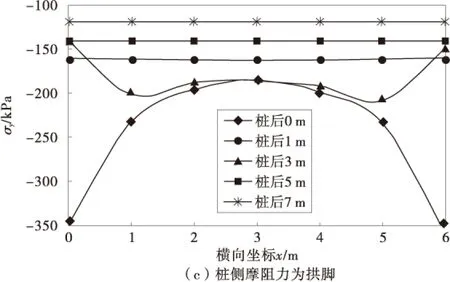
图5 不同剖面的应力σy分布曲线Fig.5 Stress distribution σy curves with different profiles

从图中可以看出有以下特点：①在不同的拱脚形式下靠近桩位置处均形成应力拱。由于本文的计算模型为悬臂式抗滑桩，在桩前没有坡前土体的抗力，桩间土体的滑塌仅为在自重应力作用而产生；②随着与桩身位置越远，桩间土的应力拱逐渐减弱，在桩后3 m的位置应力拱开始逐渐减小，到5 m和7 m的位置处基本为一条水平线。因此可知桩间土拱的拱高约为3m；③从图5(a)～图5(c)对比可知，联合拱脚和桩身拱脚的主应力曲线分布基本一致，仅在桩身位置处有所不同，而桩侧摩阻力为拱脚时在桩身位置处有明显的应力拱，在桩后其他位置处应力拱很微弱，在桩后1 m的位置处在桩侧位置处应力比其他位置处的应力都大，这是由于桩侧位置处摩阻力提供了反力，而其他位置由于桩间土体在重力作用下出现滑移，没有支撑力。

3.2 桩中心线处法向应力的分布

图6为桩中心线处法向应力的分布曲线。从曲线中可以看出，曲线均在成拱区域内急剧增大，距离桩身位置越远，曲线逐渐平缓。桩侧摩阻力为拱脚时在0～2.0 m范围内法向应力逐渐增大，在2.0 m的位置处达到了最大值。以桩身和桩侧为拱脚时的法向应力也是在桩后成拱区域出现最大值，同时两者出现最大值位置相近，进一步说明联合拱脚时以桩身提供的拱脚支撑力为主要部分，桩侧提供的支撑力较小。

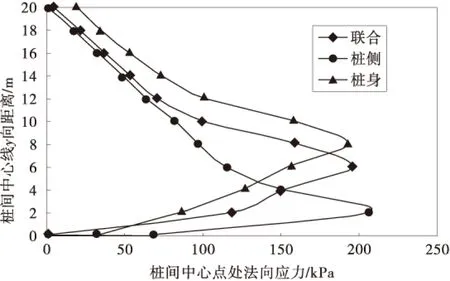
图6 桩中心线处法向应力Fig.6 Normal stresses at the center line of pile

4 影响因素的分析

4.1 黏聚力的影响

图7为桩中心线处法向应力随黏聚力的变化曲线。在联合、桩侧和桩身为拱脚的单一情况下研究桩中心线处法向应力随黏聚力的变化关系。从图中可以看出：3种不同的拱脚形式下的法向应力随着黏聚力的增大，土拱形状逐渐向中心部位收缩，土拱形状由三角形发展呈椭圆形和拱形，黏聚力在60 kPa以上对土拱的影响较小，在桩后的10 m位置以后黏聚力对土拱影响甚微；以桩侧摩阻力为拱脚的法向应力曲线土拱形成主要为三角形为主，土拱影响范围比其他两种形式都小，在本算例模型中桩截面的高度为2 m，其桩后影响范围约为6 m，在0～6 m范围内土拱效应和土体的应力偏转现象明显，在桩后6 m之后曲线变化很小。以桩身为拱脚时的法向应力变化曲线与联合拱脚曲线发展趋势基本一致，进一步证明了联合土拱中以桩身支撑为主，桩侧摩阻力提供的支撑反力较小。同时桩侧摩阻力仅在桩后一定范围内对土拱有影响，其影响深度有限，而桩身的支撑力对土拱的影响深度较深。

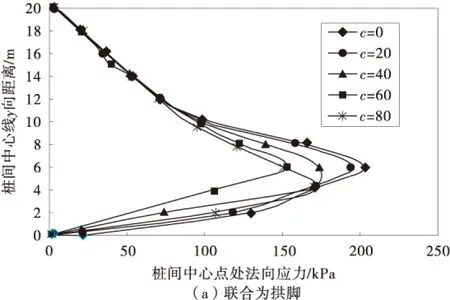
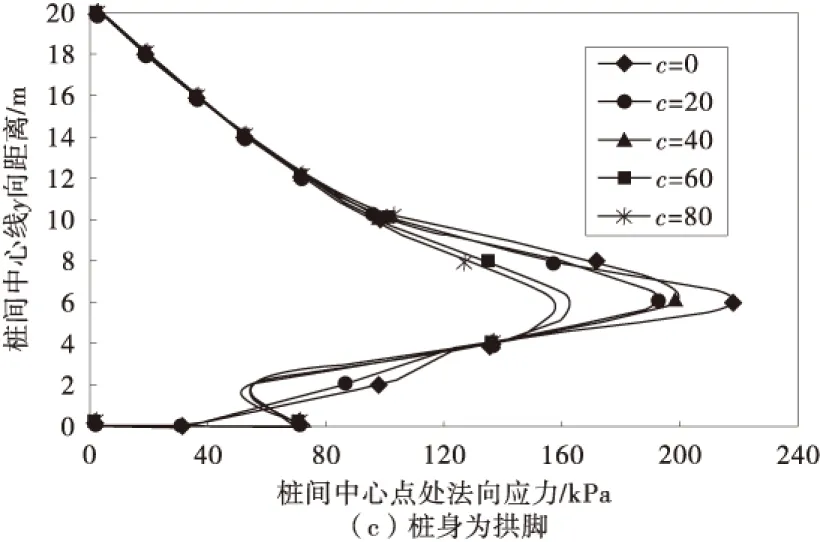
图7 桩中心点处法向应力随黏聚力的变化曲线Fig.7 Normal stresses changing with cohesion at the center point of the pile

4.2 桩间距的影响

桩间滑坡土体是否能形成土拱受诸多因素的影响，其中最为关键的两个因素为桩间距和桩截面宽度，为了研究这两个可变因素对土拱效应的影响，采用桩间距与桩截面宽度l/b来表征，在计算中l/b分别等于2，4，6，8。图8(a)为以联合为拱脚下桩间中心线法向应力随l/b的变化曲线；图8(b)为以桩身为拱脚下桩间中心线法向应力随l/b的变化曲线，因为以桩侧为拱脚情形下计算模型中不存在桩截面宽度，因此只给出联合和桩身两种情形下的变化曲线。从图中可知，随着l/b比值的增加，法向应力也逐渐增加，在桩后y=2～3m范围内应力急剧增大，应力偏转现象更为明显，但是应力偏转影响区域逐渐减小。其次以联合为拱脚是的法向应力大于以桩身为拱脚时的法向应力，随着l/b比值的增加，以桩身为拱脚时的法向应力约占联合拱脚法向应力的比例由88%变化至61%。同时随着l/b比值的增加，桩间土拱越难以形成，桩侧摩阻力对土拱形成的贡献更小。

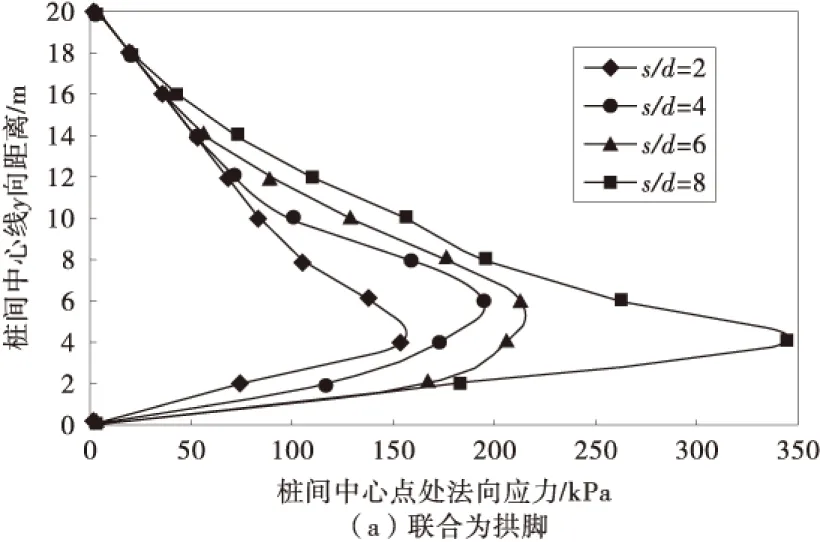
图8 桩中心点处法向应力随l/b变化曲线Fig.8 Normal stresses changing with l/b at the center point of the pile

5 结 论

1)桩间滑坡土体中土拱拱脚的支撑力由桩身和桩侧摩阻力两者共同来提供，但是主要由桩身来提供，桩侧摩阻力所提供的土拱支撑力较小，同时由于受到土体黏聚力和内摩擦角的影响，不易确定，因此拱脚支撑力理论计算中将其两者分开独立考虑欠妥。

2)桩间距对土拱效应的影响较大，随着桩间距的增大，土拱影响范围逐渐减小，但是桩间中心线上法向应力增加，土体应力偏转现象更明显，但是影响区域减小，同时随着桩间距的增大，桩身为拱脚所占联合为拱脚的法向应力也逐步减小。

3)黏聚力的增大，土拱越容易形成，但是当黏聚力增大到一定程度后土拱效应的形成受到其他的因素影响。

[1] TERZAGHI K.TheoreticalSoilMechanics[M].New York:John Wiley & Son,1943:66-76.

[2] WANG D L,YEN B C.Soil arching in slopes [J].JournalofGeotechnicalEngineeringDivision,ASCE,1974,104(GT4):493-496.

[3] 王成华,陈永波,林立相.抗滑桩间土拱力学特性与最大桩间距分析[J].山地学报,2001,19(6):556-559. WANG Chenghua,CHEN Yongbo,LIN Lixiang.Soil arch mechanical character and suitable space between one another anti-sliding pile [J].JournalofMountainScience,2001,19(6):556-559.

[4] 赵明华,陈炳初,刘建华.考虑土拱效应的抗滑桩合理桩间距分析[J].中南公路工程,2006,31(2):1-3,28. ZHAO Minghua,CHEN Bingchu,LIU Jianhua.Analysis of the spacing between anti-slide piles considering soil-arch effect [J].CentralSouthHighwayEngineering,2006,31(2):1-3,28.

[5] 王士川,陈立新.抗滑桩间距的下限解[J].工业建筑,1997,27(10):33-37. WANG Shichuan,CHEN Lixin.Anti-slide pile spacing of the lower limit equation [J].IndustrialConstruction,1997,27(10):33-37.

[6] 周德培,肖世国,夏雄.边坡工程中抗滑桩合理桩间距的探讨[J].岩土工程学报,2004,26(1):132-135. ZHOU Depei,XIAO Shiguo,XIA Xiong.Discussion on rational spacing between adjacent anti-slide piles in some cutting slope projects [J].ChineseJournalofGeotechnicalEngineering,2004,26(1):132-135.

[7] 周应华,周德培,冯君.推力桩桩间土拱几何力学特性及桩间距的确定[J].岩土力学,2006,27(3):455-457. ZHOU Yinghua,ZHOU Depei,FENG Jun.Geometrically mechanical characters of soil arch between two adjacent laterally loaded piles and determination of suitable pile spacing [J].RockandSoilMechanics,2006,27(3):455-457.

[8] 蒋良潍,黄润秋,蒋忠信.黏性土桩间土拱效应计算与桩间距分析[J].岩土力学,2006,27(3):445-450. JIANG Liangwei,HUANG Runqiu,JIANG Zhongxin.Analysis of soil arching effect between adjacent piles and their spacing in cohesive soils [J].RockandSoilMechanics,2006,27(3):445-450.

[9] 李邵军,陈静,练操.边坡桩-土相互作用的土拱力学模型与桩间距问题[J].岩土力学,2010,31(5):1352-1358. LI Shaojun,CHEN Jing,LIAN Cao.Mechanical model of soil arch for interaction of piles and slope and problem of pile spacing [J].RockandSoilMechanics,2010,31(5):1352-1358.

[10] 冯君,吕和林,王成华.普氏理论在确定抗滑桩间距中的应用[J].中国铁道科学,2003,24(6):80-82. FENG Jun,LV Helin,WANG Chenghua.Application of M.M.Promojiyfakonov theory to solution of distance between anti-slide piles [J].ChinaRailwayScience,2003,24(6):80-82.

[11] 吕庆,孙红月,尚岳全.抗滑桩桩后土拱形状及影响因素[J].哈尔滨工业大学学报,2010,42(4):629-633. LV Qing,SUN Hongyue,SHANG Yuequan.Shape of soil arch behind anti-slide piles and its major influence factors [J].JournalofHarbinInstituteofTechnology,2010,42(4):629-633.

[12] 杨明,姚令侃,王广军.桩间土拱效应离心模型试验及数值模拟研究[J].岩土力学,2008,29(3):817-822. YANG Ming,YAO Lingkan,WANG Guangjun.Study of centrifuge model tests and numerical simulation on soil arching in space of piles [J].RockandSoilMechanics,2008,29(3):817-822.

[13] 王成,王东,陈夏雨,等.桩间土拱效应离心模型试验研究[J].地下空间与工程学报,2012,8(1):33-36. WANG Cheng,WANG Dong,CHEN Xiayu,et al.Study on centrifuge model tests of soil arching effect between piles [J].ChineseJournalofUndergroundSpaceandEngineering,2012,8(1):33-36.

[14] 张永兴,董捷,黄治云.合理间距条件悬臂式抗滑桩三维土拱效应试验研究[J].岩土工程学报,2009,31(12):1874-1881. ZHANG Yongxing,DONG Jie,HUANG Zhiyun.Experimental investigation on three-dimensional soil arching effect between adjacent cantilever anti-slide piles with rational spacing [J].ChineseJournalofGeotechnicalEngineering,2009,31(12):1874-1881.

[15] 曹卫平,胡伟伟.桩承式加筋路堤三维土拱效应试验研究[J].岩土力学,2014,35(2):351-358. CAO Weiping,HU Weiwei.Experimental study of 3D soil arching in piled reinforced embankments [J].RockandSoilMechanics,2014,35(2):351-358.

[16] 刘钦,李地元,刘志祥,等.水平推力作用下抗滑桩间土拱效应影响因素的数值分析[J].中南大学学报(自然科学版),2011,42(7):2071-2077. LIU Qin,LI Diyuan,LIU Zhixiang,et al.Numerical analysis of influence factors on soil arching effect between anti-sliding piles under horizontal pushing loads [J].JournalofCentralSouthUniversity(ScienceandTechnology),2011,42(7):2071-2077.

[17] 陈福全,侯永峰,刘毓氚.考虑桩土侧移的被动桩中土拱效应数值分析[J].岩土力学,2007,28(7):1333-1337. CHEN Fuquan,HOU Yongfeng,LIU Yuchuan.Numerical analysis of soil arching effects in displaced passive piles considering lateral soil movements [J].RockandSoilMechanics,2007,28(7):1333-1337.

[18] 张建华,谢强,张照秀.抗滑桩结构的土拱效应及其数值模拟[J].岩石力学与工程学报,2004,23(4):699-703. ZHANG Jianhua,XIE Qiang,ZHANG Zhaoxiu.Arching effect of anti-sliding pile structure and its numerical simulation [J].ChineseJournalofRockMechanicsandEngineering,2004,23(4):699-703.

[19] 姜春林,李晋.微型抗滑桩土拱效应空间特征的细观力学分析[J].岩土力学,2012,33(6):1754-1760,1815. JIANG Chunlin,LI Jin.Mesomechanical analysis of spatial characteristics of soil arching effect on micro anti-slide pile aystem [J].RockandSoilMechanics,2012,33(6):1754-1760.

[20] 韩高孝,宫全美,周顺华.摩擦型岩土材料土拱效应微观机制颗粒流模拟分析[J].岩土力学,2013,34(6):1791-1798. HAN Gaoxiao,GONG Quanmei,ZHOU Shunhua.Analysis of microcosmic mechanism of soil arching in frictional geotechnical material by particle flow simulating [J].RockandSoilMechanics,2013,34(6):1791-1798.

[21] 向先超,张华,蒋国盛,等.基于颗粒流的抗滑桩土拱效应研究[J].岩土工程学报,2011,33(3):386-391. XIANG Xianchao,ZHANG Hua,JIANG Guosheng,et al.Soil arching effect of anti-slide piles based on particle flow method [J].ChineseJournalofGeotechnicalEngineering,2011,33(3):386-391.

Soil Arching of Anti-Slide Piles Based on Different Skewback Forms

REN Yongzhong, MA Shoucai

(College of Civil Engineering, Lanzhou Institute of Technology, Lanzhou 730050, Gansu, P.R.China )

At present, the research on the skewback forms of soil arching of anti-slide piles mainly focuses on 3 types of forms, including pile body, side friction of pile and the union of both. In order to research the bearing load mechanism and influencing factors of soil arching with three forms of skewback, the geotechnical analysis software package named Plaxis V8.5 was used to carry out numerical analysis. During the analysis, FEM models of three forms of skewback were established respectively. To reflect friction characteristics between side pile and soil, the interface element offered by the software was used to simulate. The results show that the pile body mainly provides the holding power for soil arching skewback of cantilever anti-slide piles, and the holding power offered by side pile is limited; with the increase of pile spacing, the soil arching is not easily formed and the proportion of normal stress when the pile body is skewback decreases gradually in the proportion of normal stress when pile body and side friction of pile are united as the skewback.

geotechnical engineering; anti-slide piles; soil arching; skewback; pile spacing; numerical analysis

2015-10-13；

2015-11-19

任永忠(1986—)，男，甘肃平凉人，博士，主要从事支挡结构以及滑坡防治工程的治理等研究。E-mail：renyz518@163.com。

10.3969/j.issn.1674-0696.2016.01.20

TU473

A

1674-0696(2016)01-101-06