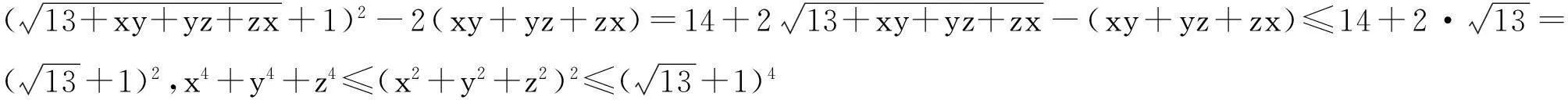2016年IMO不等式题的巧思妙证
2016-05-24南昌大学附属中学330047
中学数学研究(江西) 2016年5期
南昌大学附属中学 (330047) 周 辉
2016年IMO不等式题的巧思妙证
南昌大学附属中学(330047)周辉
本文中,笔者对新近出炉的一些国际数学奥林匹克中的不等式题潜心研究,精心证明,悉心撰写 , 以飨读者.
例1(2016年摩尔多瓦数学奥林匹克)已知a,b,c是满足a2+b2+c2+ab+bc+ca=6的正数,求a+b+c的最大值.



例3(2016年土耳其数学奥林匹克)已知x,y,z是正数,求证: x4y+y4z+z4x+xyz(x3+y3+z3)≥(x+y+z)(3xyz-1).
证明:由x3+2y3≥3xy2,y3+2z3≥3yz2,z3+2x3≥3zx2,得x3+y3+z3≥xy2+yz2+zx2,x4y+y4z+z4x+xyz(x3+y3+z3)≥x4y+y4z+z4x+xyz(xy2+yz2+zx2)=x(x3y+y2z3+1)+y(y3z+z2x3+1)+z(z3x+x2y3+1)-(x+y+z)≥3x2yz+3y2zx+3z2xy-(x+y+z)=(x+y+z)(3xyz-1).



例6 (2016年韩国数学奥林匹克)已知x,y,z≥0,(x+y-1)2+(y+z-1)2+(z+x-1)2=27,求x4+y4+z4的最大值和最小值.