超低空空投侧风安全边界确定方法

赵世伟, 孙秀霞, 刘日, 王栋, 徐光智

(空军工程大学 航空航天工程学院, 陕西 西安 710038)



超低空空投侧风安全边界确定方法

赵世伟, 孙秀霞, 刘日, 王栋, 徐光智

(空军工程大学 航空航天工程学院, 陕西 西安 710038)

摘要:执行超低空重装空投任务的大型运输机极易受到扰动风的影响从而威胁飞行安全。根据小扰动线性化方法,从载机安全性出发,提出侧风安全边界的确定方法:载机受扰后的瞬态响应峰值不能过大;稳定飞行时,舵面应能提供足够的操纵力和力矩,以补偿风效应产生的附加气动力和力矩。仿真计算结果表明,该方法对超低空空投条件具有良好的分析预测能力。

关键词:大型运输机; 超低空空投; 侧风扰动; 风强度安全边界

0引言

近年来,随着对空投准确性和任务能力要求的提高,大型运输机超低空重装空投以其投放精度高、可躲避敌方雷达探测等优势,日益引起军方的重视[1-2]。相对于常规飞行,超低空、低速重装空投的恶劣飞行条件使得飞机的抗干扰能力变差。已有的空投和风洞试验表明[3]:空投场地的扰动风对运输机的安全性和任务完成性的影响是不容忽略的。在所载重型设备向出舱口移动的过程中,飞机飞行状态极不稳定,甚至因受到低空大气扰动的影响导致产生灾难性的后果[4-8]。因此,对风扰动下的大型运输机重装空投的安全性能问题进行研究具有重要意义。

当前,针对运输机重装空投的动力学建模[4-6]、地面效应的影响[7-8]、控制律设计[8-10]、空投器材等相关方面的研究已取得了一定的成果。但关于大气扰动作用下的运输机重装空投的安全性及空投过程中扰动风安全边界的确定尚无专业性的研究。

本文从运输机的全量动力学方程出发,根据风扰动的作用结果,建立了侧风扰动下的运输机横侧向运动模型。从载机受扰后的瞬态响应峰值限制和舵面的静操纵能力限制出发,提出了安全约束条件。在此基础上,推导出了侧向扰动风安全边界确定方法。

1侧风扰动下的飞机横侧向运动建模

1.1横侧向模型的线性化

由空投运输机的全量动力学模型[6]可得,运输机空投时在基准运动状态下的横侧向运动方程为:

(1)

式中:Y为侧力;LA为滚转力矩;NA为偏航力矩;其余符号的定义参见文献[11]。

由于一般飞机的侧向偏离y和偏航角ψ不对飞行安全构成威胁,且作用于载机上的气动力与y和ψ无关,因此,在下面的线性化推导中不再考虑式(1)中的后两式。

将Y,LA和NA对基准运动的泰勒级数一阶展开得:

(2)

式中:rA,pA分别为载机相对大气的偏航角速度和滚转角速度;x*为x对*的偏导数,如Yβ为侧力Y对侧滑角β的偏导数。

(3)

与β,rA,pA,δr,δa相关的气动偏导数的意义与文献[11]相同。

大气扰动下,载机侧滑角变化量可表示为[4]:

(4)

为表示方便,引入如下动力系数:

(5)

将式(2)～ 式(5)代入式(1),可得载机横侧向运动的标准矩阵形式:

(6)

由线性系统知识可知,式(6)可写为一般形式如下:

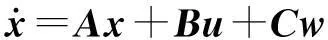
(7)

1.2线性化模型的验证

在基准运动状态下,对系统施加侧风vw=4 m/s、持续时间为1 s的脉冲扰动。横侧向非线性模型的仿真结果与线性化模型的仿真结果对比如图1所示(“□”表示施加侧向扰动风时刻)。

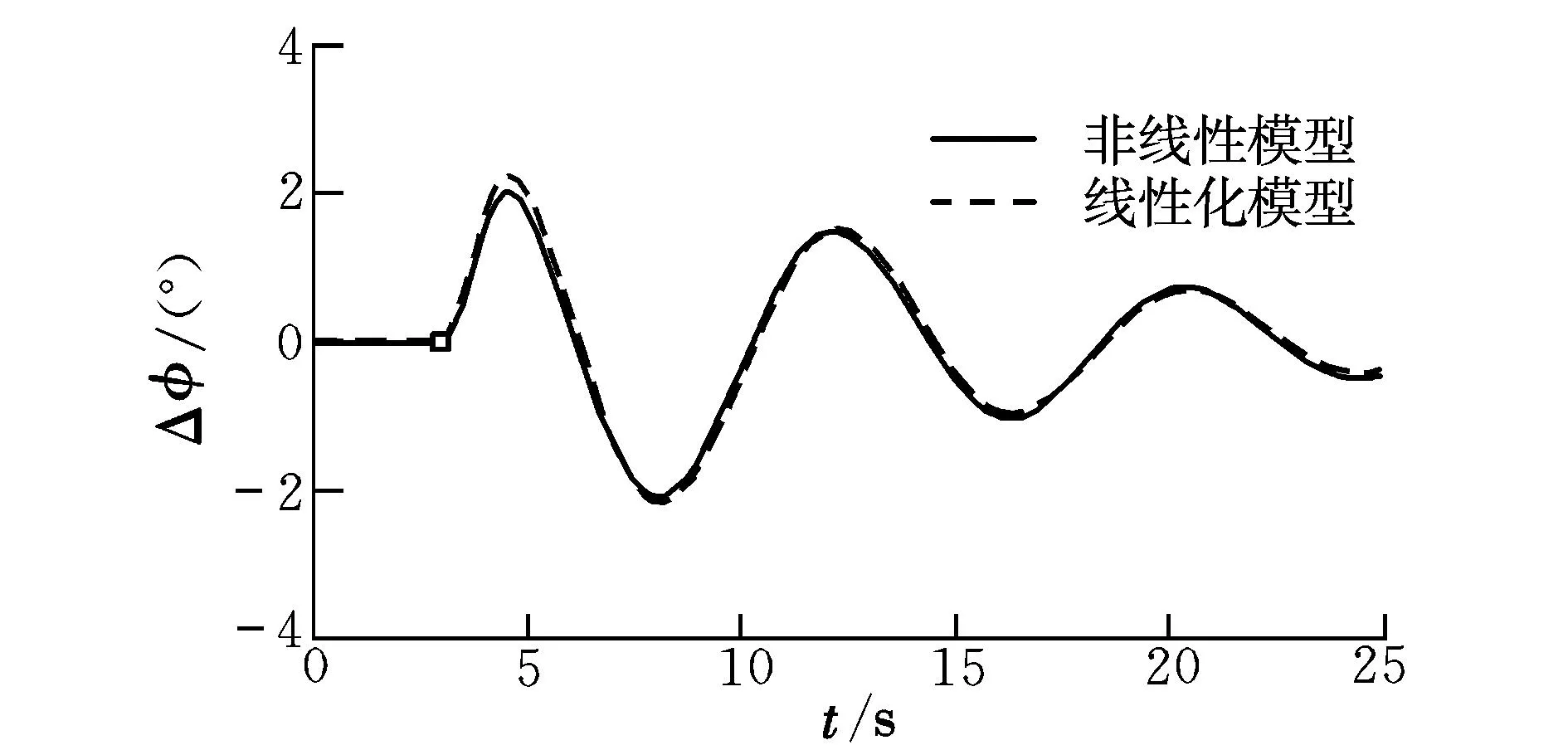
图1　滚转角响应对比Fig.1　Comparison of roll angle responses

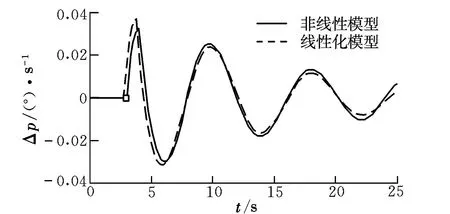
图2　滚转角速度响应对比Fig.2　Comparison of roll rate responses

可以看出,在相同的侧向扰动风作用下,基于非线性模型的横侧向响应与线性化模型的仿真结果具有较强的一致性。因此,利用线性化模型研究飞机的横侧向受扰特性是合理的。

2侧风强度安全边界确定

由大型运输机重装空投条件分析可知,若载机带货平飞过程中遭遇强侧风,从载机的安全性和任务完成性出发,需要满足以下两个约束条件:

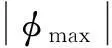
(2) 在侧风环境下,要保证载机航向稳定,副翼和方向舵应具备足够的静操纵力,能使载机带侧滑和倾斜稳定飞行。

要满足以上条件,取决于载机的阻尼特性和副翼及方向舵的静操纵能力。

2.1依据滚转角约束条件确定侧风强度安全边界

当只考虑侧风的扰动作用时,式(7)可简化为:

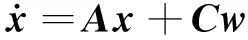
(8)

根据约束条件(1),侧风扰动时,载机滚转角的瞬态峰值应满足[9]:

(9)

由式(7)并利用卷积定理可得:

(10)

式中:eAt=Φ(t)=L-1[(sI-A)-1]为系统的状态转移矩阵;x(0)为载机初始状态;其余各符号含义同式(7)。则可分两种情况对滚转角φ(t)进行分析:

(1)若滚转角φ(t)在(0,5) s时间区间内有极值,则由极值存在的必要条件得:

(11)

对于右侧风φmax(vw)为正;反之为负。

(2)若在(0,5) s时间区间内滚转角单调变化,则滚转角的峰值发生在t=5 s时。将t=5 s代入式(10),即可得到滚转角峰值φmax(vw)。φmax(vw)是侧风vw的一元函数。

将上述得出的φmax(vw)代入式(9),即可求得滚转角安全性条件限制的侧风强度安全边界。

2.2依据舵面的静操纵能力限制确定侧风强度

安全边界

在货物解锁前,载机应处于稳定的定直平飞运动状态。若遭遇侧风,为使航迹速度对准预定空投区域,需要载机带侧滑和倾斜稳定飞行,如图3所示。

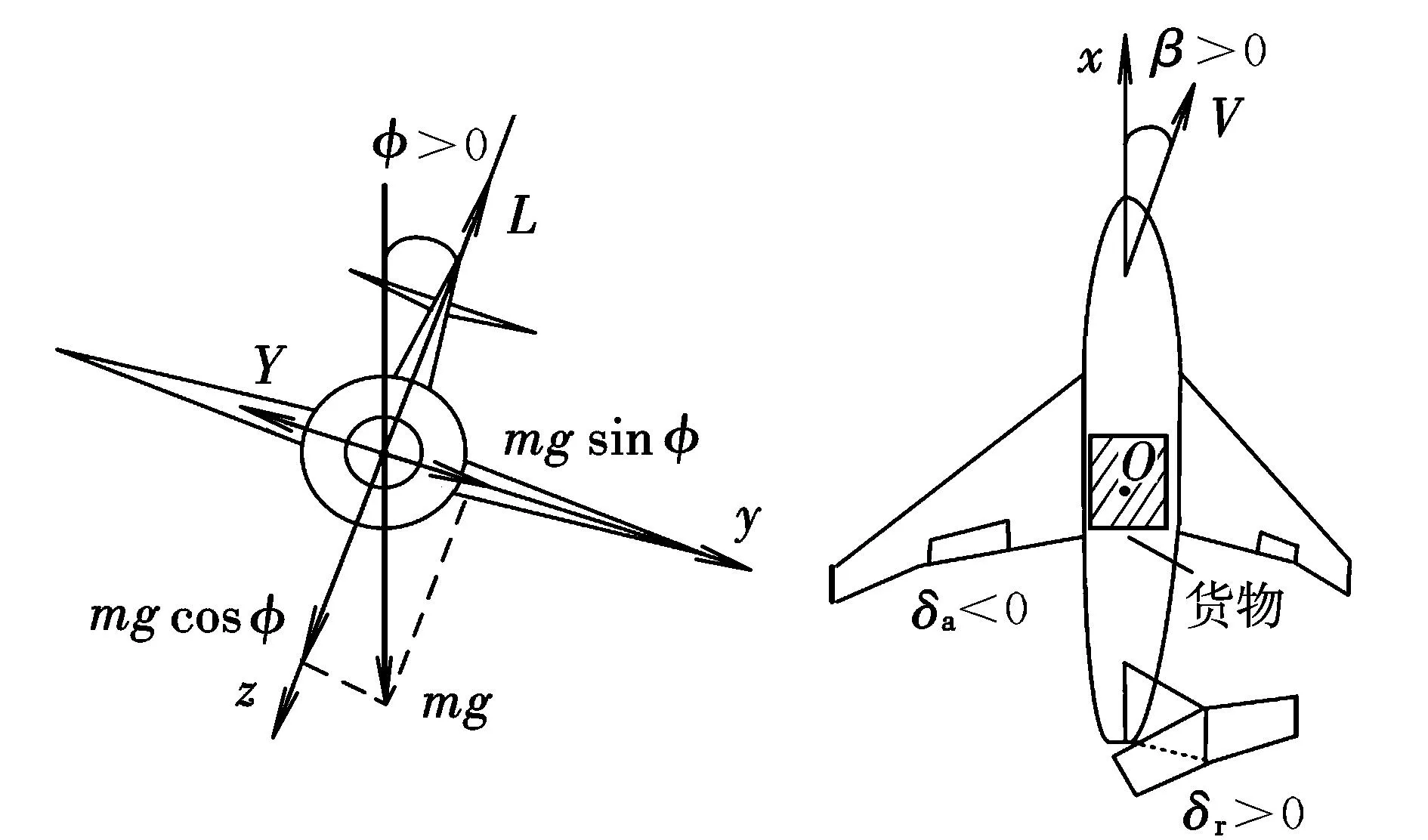
图3　定常直线侧滑飞行时作用在载机上的力Fig.3　Force on carrier in constant steady straight sideslip

可以看出：侧滑时的侧力通过倾斜载机,利用重力的分量来平衡;侧滑引起的横侧向力矩,需要副翼和方向舵偏转的操纵力来平衡:

(12)

式中:Clφ,Cnφ是与地面效应相关的气动导数[8];其余各符号含义参见文献[11]。

由铅垂方向的平衡条件可得mg≈L,从而可得mgsinφ≈Lsinφ,则式(12)可简化为:

(13)

在各气动导数为已知的情况下,上式包含4个未知数β,φ,δa,δr。将式(13)化为如下形式:

(14)

其中:

可见,载机定值侧滑飞行过程中所需的副翼偏转量δa、方向舵偏转量δr以及滚转角φ都与侧滑角β成正比。于是,根据约束条件(2)有:

(15)

式中:δr,max,δa,max分别为方向舵和副翼的最大偏转角;φmax为空投过程中载机滚转角的安全上界[9]。

则由式(14)和式(15)可确定侧滑角的允许边界:

(16)

由侧滑角与侧风的关系得:

(17)

则由式(16)、式(17)可确定侧风强度的安全边界为:

(18)

3仿真算例

以某大型运输机为例,在飞行速度80 m/s(中高空为110 m/s)、襟翼开度25°、载货质量8 000 kg、采用单列单投的方式进行空投的条件下,依据2.1中的约束条件,针对特定的空投任务,通过大量的仿真试验进行循环迭代,来确立满足约束条件(1)的安全边界,利用式(16)～式(18)求得满足约束条件(2)的安全边界。

从载机安全性考虑,取侧向扰动风安全边界为上述两者的较小者。计算得到在不同高度下满足载机安全性要求的侧向扰动风边界见表1。

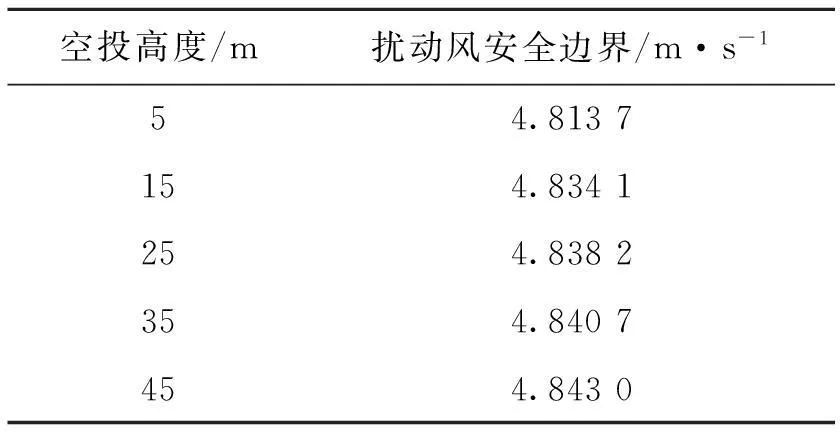
表1　某大型运输机在超低空的扰动风安全边界

对于在中高空执行空投任务的运输机,由于不存在翼尖触地的危险,因此,对侧向扰动风的安全约束只需要满足约束条件(2)即可。求得的侧向扰动风安全边界见表2。

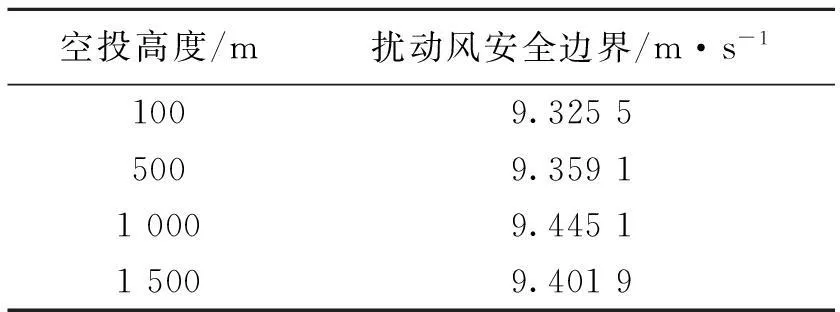
表2　某大型运输机在中高空的扰动风安全边界

根据以上计算所得的安全边界,对该运输机在不同高度进行空投时,受到侧向扰动风vw=4.8 m/s,vw=9.4 m/s两种情况进行仿真,其滚转角响应如图4和图5所示。

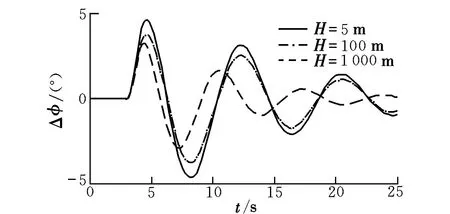
图4　vw=4.8 m/s时的滚转角响应Fig.4　Roll angle responses when vw=4.8 m/s

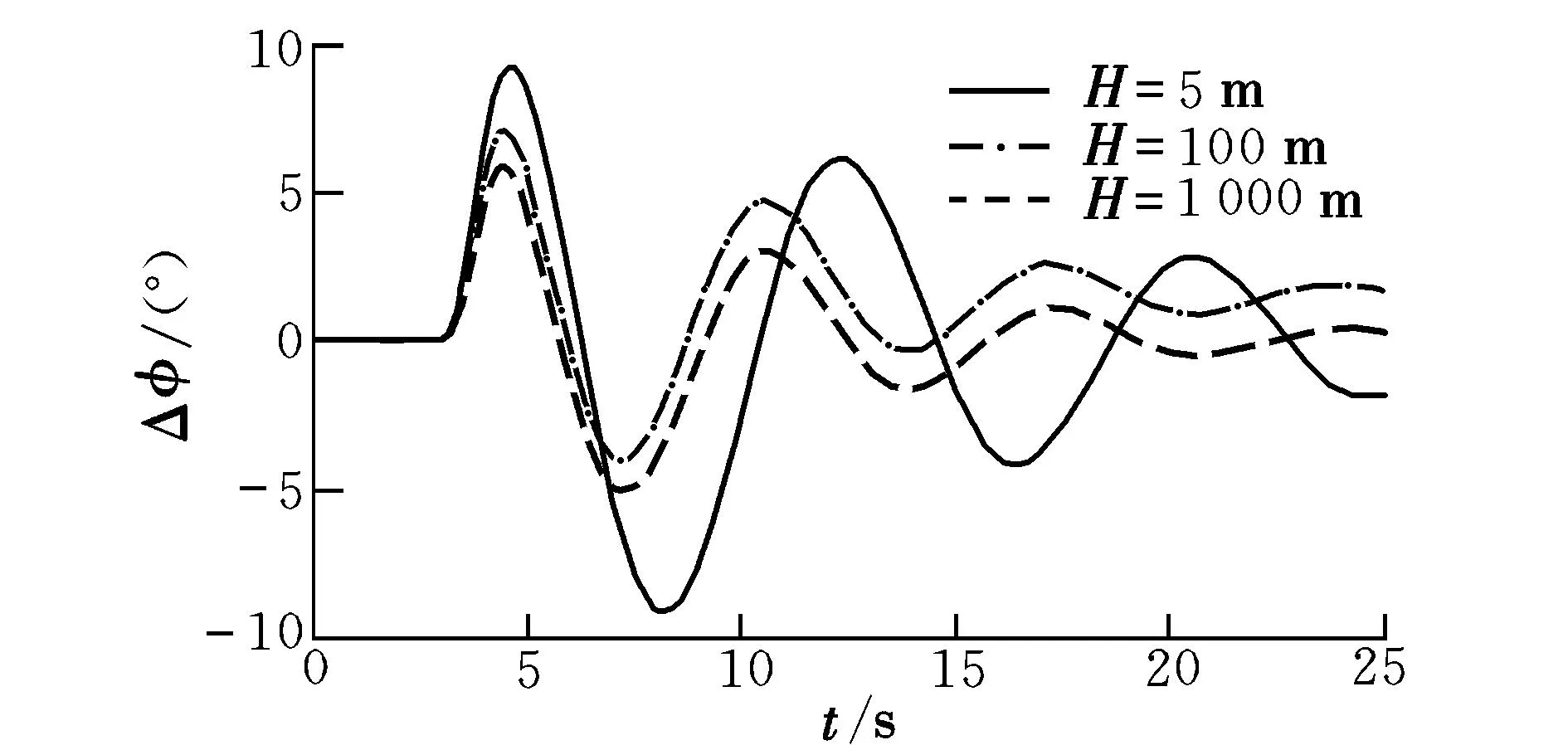
图5　vw=9.4 m/s时的滚转角响应Fig.5　Roll angle responses when vw=9.4 m/s

可以看出,相对于中高空执行空投任务的运输机,超低空空投载机所能承受的侧向扰动风更小。这是由于在中高空,影响运输机抗侧风能力的主要因素是升力系数等参数(由式(14)可以看出升力系数对抗侧风能力的影响),而随着空投高度的降低,地面效应对运输机产生的影响愈发显著。

4结束语

本文针对运输机超低空易受侧风扰动这一工程实际问题,提出了满足载机安全性的允许扰动侧风强度确定方法。通过对某大型运输机为实例的仿真计算,表明超低空空投的运输机对于扰动风更为敏感,因此对扰动风强度的研究是十分必要的。

参考文献：

[1]Michael Henry,Kristen Lafond.Gregory noetscher development of a 2,000～10,000 lbs improved container delivery system[R].AIAA-2009-2909,2009.

[2]郝广庆.国内外重装空投技术的现状和发展[C]//中国航空学会全国第10届安全救生学术交流会文集.杭州:湖北省科学技术协会,2006:115-118.

[3]Bury Y,Morton S,Charles R.Experimental investigation of the flow field in the close wake of a simplified C-130 shape a model approach of airflow influence on airdrop [R].AIAA-2008-6415,2008.

[4]Liu Ri,Sun Xiuxia,Dong Wenhan.Dynamics modeling and control of a transport aircraft for ultra-low altitude airdrop [J].Chinese Journal of Aeronautics,2015,28(3):478-487.

[5]刘日,孙秀霞,李大东,等.反馈线性化超低空空投抗侧风滑模控制律设计[J].应用科学学报,2014,32(11):311-318.

[6]冯艳丽.大型运输机重型货物出舱过程建模与控制[D].西安:西北工业大学,2009.

[7]刘日,孙秀霞,董文瀚,等.地面效应对超低空空投载机动力学特性的影响[J].飞行力学,2014,32(4):289-293.

[8]杨雨,陆宇平,戴正升.基于动态逆的超低空空投抗侧风控制器设计[J].飞行力学,2013,31(1):37-41.

[9]杨朝星.超低空空投飞行控制系统性能评估[D].南京:南京航空航天大学,2010.

[10]肖亚伦,金长江.大气扰动中的飞行原理[M].北京:国防工业出版社,1993:47-92.

[11]蔡满意.飞行控制系统[M].北京:国防工业出版社,2007.

(编辑：崔立峰)

Determination of safety-boundary of cross-wind for ultra-low altitude airdrop

ZHAO Shi-wei, SUN Xiu-xia, LIU Ri, WANG Dong, XU Guang-zhi

(Aeronautics and Astronautics Engineering College, AFEU, Xi’an 710038, China)

Abstract:A transport aircraft performing the task of ultra-low altitude airdrop is likely to be threatened by wind disturbance from the safety of the transport, a method to determine the safety-boundary of cross-wind disturbance for ultra-low altitude airdrop is proposed according to the small perturbations method: The transient peak attitude after disturbance should not be too large to influence the flying safety; and the control surface can provide enough operating force and moment to compensate the disturbance effect. The simulation results show that the method could effectively analyze and evaluate the airdrop conditions.

Key words:ransport aircraft; ultra-low altitude airdrop; cross-wind disturbance; wind strength safety-boundary

中图分类号：V212.1

文献标识码：A

文章编号：1002-0853(2016)01-0022-04

作者简介:赵世伟(1992-),男,甘肃庆阳人,硕士研究生,主要研究方向为飞机飞行品质;孙秀霞(1962-),女,山东潍坊人,教授,博士生导师,博士,主要研究方向为现代鲁棒控制和飞行控制。

基金项目:国家自然科学基金资助(60904038);航空科学基金资助(20141396012)

收稿日期:2015-05-11;

修订日期:2015-06-03; 网络出版时间:2015-10-14 17:18