考虑爬坡特性的短期风电功率概率预测
2016-05-23柯德平孙元章崔明建
甘 迪,柯德平,孙元章,崔明建
(武汉大学 电气工程学院,湖北 武汉 430072)
0 引言
近年来,随着风电并网规模的逐渐增大,风电的随机性和波动性对电网的冲击和威胁日益成为不可忽视的问题[1]。 风电功率短期概率预测[2-3]是解决这一问题的方法之一,其不仅能提供预测结果的波动范围,还能估计出每一个取值出现的概率,相比于确定性预测更能提供丰富的不确定信息,因此广泛应用于电力系统概率最优潮流计算[4-5]、电力系统静态安全评估[6-7]等研究领域中,有助于电力调度部门提前安排发电计划,以保证合格的电能质量,确保电力系统安全稳定运行。
目前常见的风电功率概率预测方法有:分位点回归法[8]、贝叶斯推断法[9]、上下边界估计 LUBE(Lower Upper Bound Estimation)法[10]和核密度估计 KDE(Kernel Density Estimation)法[11-12]等。 文献[8]建立了基于支持向量机和分位点回归的风电功率区间预测模型,通过支持向量机确定每一个分位点的回归函数。尽管该模型没有先验的分布假设,能提供稳定的预测信息,但需事先设定离散的不同分位点,模型得到的概率密度函数是离散的,对每一分位点建模也增加了模型复杂度。文献[9]提出一种分量稀疏贝叶斯学习方法,根据核方法和贝叶斯框架实现概率预测,但该模型需对风电功率的先验分布作出假设,引入了经验误差。文献[10]建立了基于神经网络和LUBE的预测区间估计模型,神经网络直接输出设定的置信度下估计区间的上下界,模型算法较简单实用,但该模型无法提供概率密度函数和累积密度函数,不确定信息表现方式单一。不同于上述方法,核密度估计是一种统计学非参数估计方法,该方法不限于事先定义的分位点,无需假设先验分布,能够提供每一个时间尺度的连续概率分布函数。文献[11]在神经网络点预测的基础上,通过一维核密度估计得到了较好的概率预测结果,但该模型在风电功率变化剧烈的时段误差较大,区间平均宽度与平缓段相比显著增加。这种风电功率变化剧烈的现象被称为“风电爬坡事件”[13-19],由于其强烈的随机性和波动性,降低了该时段风电功率预测的精度。
本文在一维核密度估计的基础上,通过考虑风电爬坡特性对预测时刻误差的影响,将一维核密度估计扩展为二维,提出一种改进的提前1 h风电功率概率预测方法。首先介绍了风电爬坡事件的定义和特性,提出一种互补组合预测思路,并采用具有较好时频局部特性的小波神经网络[20-21]建立风电功率确定性预测模型。然后根据风电功率预测误差和风电功率爬坡率的分布特点,对每一个功率分区建立二维核密度估计模型,由联合分布求取条件分布,得到风电功率的概率预测区间。仿真结果表明,本文模型能够有效提高风电功率概率预测质量,为风电功率概率预测提供了一种新的研究思路。
1 风电爬坡特性
1.1 风电爬坡事件
风电爬坡事件是指风电功率在短时间内急剧变化的现象,其包含3个关键特征:爬坡方向、爬坡时间和爬坡幅值。爬坡方向有2种:发生爬坡时风电功率增大为上行爬坡事件,反之为下行爬坡事件。爬坡时间和爬坡幅值分别为爬坡发生的持续时间和爬坡过程中风电功率的变化值。目前国际上并没有统一的爬坡数学定义,文献[14]列举了4种定义,这里介绍其中常用的2种。
定义 1:设 P(t)和 P(t+Δt)分别为 t时刻和 t+Δt时刻的风电功率值,TR为预先设定的阈值,一般取风电场额定装机容量的百分比。当满足

时判定风电爬坡事件发生。Zt+Δt为t+Δt时刻的爬坡率,反映了该时刻的爬坡严重程度。
定义2:设pt为风电功率信号,定义如下滤波信号

当时发生上行爬坡事件,当时发生下行爬坡事件,如图1所示。参数c为滤波阶数,一般取2或 5,本文取c=2。

图1 风电爬坡事件定义2示意图Fig.1 Schematic diagram of Definition 2 for wind power ramp event
在风电爬坡事件的研究中,定义1和定义2各有优势:定义1对原始信号建模,预测得到的信号受噪声影响较大,即使在风电功率平缓处预测误差也可能较大;定义2对滤波信号建模,虽然受噪声影响较小,信号更加平滑,能弥补定义1的缺陷,但定义2经过滤波后,难以有效探知爬坡拐点。
1.2 风电爬坡特性
风电爬坡事件是风电功率随机性和波动性的极端表现。由于该事件发生时段风电功率的非线性远远高于非发生时段,两时段风电功率时间序列的特性变化较大,因此未考虑爬坡特性的传统方法在预测爬坡发生时段的风电功率时往往误差较大。
本文从3个方面考虑风电爬坡特性对风电功率预测精度的影响,分别提出如下改进方法。
(1)风电爬坡事件发生时,风电功率信号的噪声显著增加,增加了预测的难度。因此,在进行风电功率确定性预测时,可结合风电爬坡事件2种定义的优势,提出如下互补组合预测思路:根据定义1从原始信号角度单步预测风电功率;根据定义2将原始信号变换为滤波信号,用单步预测替代多步预测提高预测精度,将滤波预测结果反变换得到风电功率预测结果。二者经线性加权平均计算,得到短期风电功率确定性预测结果。
(2)风电爬坡事件属于突发事件,其发生频率较低,这意味着对一般的风电功率时间序列而言,发生爬坡的序列长度占总序列长度的比例较小,爬坡区域的数据分辨率较低。因此在选择(1)中的确定性预测模型时,需充分考虑这一爬坡特性。小波神经网络(WNN)是一种基于小波分析的前馈神经网络,综合了小波变换和神经网络的优点,能够自适应地以高分辨率学习风电功率变化平缓的区域,以低分辨率学习风电爬坡区域,提高爬坡区域的风电功率预测精度,理论上比一般神经网络更适合考虑爬坡特性的风电功率预测。
(3)风电爬坡率是度量爬坡严重程度的指标,一般情况下,爬坡率越大,风电功率变化越快,非线性越强,预测误差越大。即非爬坡区域和爬坡区域的风电功率预测误差往往不同,前者一般小于后者。而一维核密度估计将二者合在一起估计,高估了非爬坡区域的误差,低估了爬坡区域的误差。因此,可以将传统的一维核密度估计扩展为二维,考虑风电爬坡率对误差分布的影响,求出风电爬坡率和风电功率预测误差的联合概率分布,以提高短期风电功率概率预测精度。
2 小波神经网络
设 WNN 的训练集为 D={(xi,yi),i=1,2,…,n},其中xiϵRk和yiϵR分别为模型输入和输出,则隐含层神经元数为K的WNN模型可表示为:

其中,wj为第j个隐含层与输出层的连接权值;ψj为小波基函数,本文取 Marlet函数,即 ψ(λ)=cos(1.75λ)×exp(-λ2/2);aj为 ψj的伸缩因子;wij为输入层与第j个隐含层的连接权值;bj为ψj的平移因子。WNN基于误差函数极小化原理,其3层拓扑结构如图2所示。

图2 3层WNN拓扑结构图Fig.2 Topology of three-layer WNN
3 二维核密度估计
核密度估计法一般在风电功率确定性预测的基础上,将预测功率分区,对每一分区估计预测误差分布[11]。误差e的概率密度函数为:

其中,N为样本数;h为带宽;K(·)为核函数。
当一维核密度估计扩展为二维时,设待预测时刻为t,建立t-1时刻的风电爬坡率Zt-1和风电功率预测误差et的二维核密度估计模型,其联合概率密度函数为:

其中,hZ和he分别为爬坡率和误差的带宽。
二维核密度估计求解风电功率概率预测问题的具体步骤如下。
步骤1 将风电功率的实际值ytrue和预测值y作为样本,计算出每一时刻t的预测误差et和该时刻已知的t-1时刻的风电爬坡率Zt-1。
步骤2 采用二次划分的方法,对风电功率预测值进行分区。首先对风电功率预测值等间隔划分,记ymin、ymax和Δy分别为风电功率预测值的最小值、最大值和差值,则划分区间Di和区段数d为:

上述一次划分的区间可能出现部分区间样本点过少的情况,为此可将部分相邻的区间合并,通过二次划分保证每一个区间均满足样本数目要求。
步骤3 对每一个Di,根据式(5)计算风电爬坡率Zt-1和风功率预测误差et的二维核密度估计,求出联合概率密度函数 f(Z,e)。
步骤4 由f(Z,e)计算出Zt-1=z时误差的条件概率密度函数f(et|Zt-1=z)。其方法是,找到与z最近的估计点(各估计点间距为带宽hZ),该点对应的误差断面经三次样条插值即可求出f(et|Zt-1=z)。
步骤5 对f(et|Zt-1=z)积分得到et的累积分布函数 F(et),根据风电功率预测值 yt和 yt-1,在给定的置信度下即可求出风电功率的置信区间。
4 风电功率概率预测模型
本文提出了一种短期风电功率概率预测模型,采用WNN实现风电功率确定性预测,并在其基础上采用二维KDE实现风电功率概率预测。模型流程图如图3所示,建模过程如下。
(1)将原始风电功率信号pt(表示为实际风电功率占总装机容量的比例,ptϵ[0,1])按式(2)滤波得到滤波信号,取c=2。
(2)依据定义1对pt建立WNN1单步预测模型,以t时刻及之前的风电功率值预测t+1时刻的风电功率,得到预测结果y1;依据定义2对建立 WNN2单步预测模型,以t-2时刻及之前的滤波值预测t-1时刻的滤波值,再根据式(2)反变换得到t+1时刻的风电功率预测结果y2。2个WNN模型的隐含层神经元数均设置为10。则组合风电功率确定性预测结果为 y=(y1+y2) /2。

图3 风电功率概率预测流程图Fig.3 Flowchart of probabilistic wind power forecasting
(3)根据y对功率分区,分区采用二次划分的方法,首先按0.1的步长对功率一次划分,得到10个分区,然后合并那些样本点过少的分区,使每一个分区满足样本个数要求。
(4)对每一个分区,计算其风电爬坡率Zt-1和风功率预测误差et的二维核密度估计,带宽范围均为0.005~0.015,核函数选择高斯核函数。根据联合概率分布求取条件概率分布,实现风电功率概率预测。
5 算例分析
5.1 模型评价指标
本文引入可信度、区间平均宽度和技巧得分3个概率预测评价指标来评价本文所提概率模型的有效性。
(1) 可信度[10],用于评价置信区间是否可信,即:

其中,R(1-α)为置信度 1-α 下的可信值;g 为样本的数目;ξ(1-α)为置信度1-α下实际风电功率值落入预测区间的个数。
(2) 区间平均宽度[3],用于评价概率预测聚集概率信息的能力,即:

其中,I(1-α)为置信度 1-α 下的区间平均宽度为第i个测试样本在置信度1-α下预测区间的宽度。
(3) 技巧得分[2],用于综合评价预测模型,即:


其中,SC为技巧得分;1-αi为置信度;Nα为分位点的个数;y*s为第 s 个样本的预测值;为置信度1-αi对应的分位数。
以上3个评价指标中,和I取值越小越好,SC取值越大越好。
5.2 数据描述
本文选择爱尔兰电力传输系统Eirgrid提供的爱尔兰地区某风电场群2014年1—7月的风电功率数据进行算例分析,风电总装机容量为2000 MW,时间分辨率为1 h,截取7个月内一段含5000 h的数据。为方便处理,将风电功率值均表示为占风电总装机容量的比例。二维核密度估计要求有较大的样本规模,以保证样本的统计规律趋近于总体的分布规律,因此将数据分为3个子集:前300个数据作为训练集,用于训练WNN确定性预测模型;其后4500个数据作为误差样本集,用于预测并生成二维核密度估计所需的误差样本;最后200个数据作为测试集,用于验证本文方法的有效性。
5.3 模型预测结果
图4和表1为短期风电功率确定性预测结果。为验证模型有效性,本文还采用只用一种定义建立WNN预测模型以及用BP神经网络[22]建立组合定义预测模型进行仿真作为对比。

图4 风电功率确定性预测结果Fig.4 Results of deterministic wind power forecasting

表1 预测结果对比Table 1 Comparison of forecasting results
由图4和表1可知,本文提出的WNN组合定义预测方法的平均绝对百分比误差(MAPE)为9.83%,小于BP组合定义预测、WNN定义1预测和WNN定义2预测,说明考虑爬坡特性的方法(1)和方法(2),即采用组合定义以及采用WNN建模均可有效提高风电功率确定性预测精度。
将误差样本集的风电功率预测值进行分区,首先以0.1的间隔进行一次划分,得到10个区段;将部分样本点过少的区段合并,经二次划分后得到6个区段,即 D1=[0,0.1)、D2=[0.1,0.2)、D3=[0.2,0.3)、D4=[0.3,0.4)、D5=[0.4,0.5)、D6=[0.5,1)。 分别计算每一个区段预测误差和风电功率爬坡率的联合概率分布。图5为第3区段经三次样条插值法得到的联合概率密度函数和联合分布函数图。

图5 第3区段二维概率分布Fig.5 Two-dimensional probability distribution in Section 3
遍历测试集的每一个点,根据其预测值选择功率分区及相应二维联合密度函数,根据对应的风电功率变化率计算条件概率密度函数,积分得到累积概率分布函数。按照置信度求出置信区间,将每一个点的区间包络线连接起来,即得到风电功率概率预测结果。为研究模型有效性,本文采用文献[11]的一维核密度估计作为对比。图6和图7分别为置信度90%和70%的概率预测结果。
由图6和图7可知,在相同置信度下,二维KDE和一维KDE均能有效实现风电功率的概率预测,但二维KDE的置信区间在多数情况下比一维KDE要窄,尤其在风电功率取极大极小值附近更为明显,说明本文模型能有效提高概率预测精度。

图6 概率预测结果(90%置信度)Fig.6 Results of probabilistic forecasting(90%confidence)
为定量验证模型有效性,本文计算了2种方法在不同置信度下的可信度和区间平均宽度,如表2所示。从表2可以看出,无论是可信度还是区间平均宽度,在相同置信度下,二维KDE基本优于一维KDE。说明与一维核密度估计相比,本文模型的概率预测结果具有更高的精度。

图7 概率预测结果(70%置信度)Fig.7 Results of probabilistic forecasting(70%confidence)
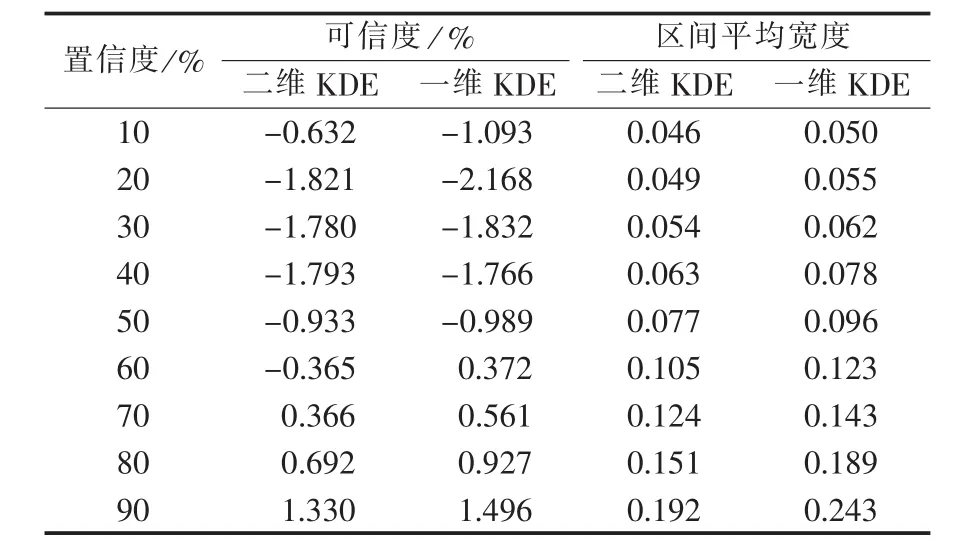
表2 可信度和区间平均宽度对比Table 2 Comparison of reliability and average interval width
本文还根据式(10)、(11)计算了2种方法的技巧得分,该指标综合考虑了可信度和区间平均宽度,可有效用于综合评价概率预测模型。经计算可得,二维KDE的技巧得分为-0.197,大于一维KDE的技巧得分-0.221,说明二维KDE的综合评价优于一维KDE,验证了本文模型的有效性和优越性。
综上所述,本文模型能够在保证置信区间可信的前提下,增加可信度,并减小区间宽度,改善风电功率概率预测的精度。
6 结论
本文提出了一种考虑风电爬坡特性的短期风电功率概率预测方法,首先根据风电爬坡事件的不同定义的优劣性提出组合预测思路,然后考虑到风电爬坡事件发生频率小、数据分辨率低的特性选择小波神经网络建立确定性预测模型,最后考虑到风电爬坡率与风电功率预测误差的关系建立了二维核密度估计概率预测模型,通过仿真算例验证了模型可有效提高风电功率概率预测精度。
参考文献:
[1]雷亚洲.与风电并网相关的研究课题[J].电力系统自动化,2003,27(8):84-89.LEI Yazhou.Studies on wind farm integration into power system[J].Automation of Electric Power Systems,2003,27(8):84-89.
[2]PINSON P,NIELSEN H A,MOLLER J K,et al.Non-parametric probabilisticforecastsofwind power:required propertiesand evaluation[J].Wind Energy,2007,10(6):497-516.
[3]SIDERATOS G,HATZIARGYRIOU N D.Probabilistic wind power forecasting using radial basis function neural networks[J].IEEE Transactions on Power Systems,2012,27(4):1788-1796.
[4]鲍海波,韦化.基于无迹变换的含大规模风电场电力系统概率最优潮流计算[J].电力系统自动化,2014,38(12):46-53.BAO Haibo,WEI Hua.Probabilistic optimal power flow computation in powersystemsincluding large-scale wind farms based on unscented transformation [J].Automation of Electric Power Systems,2014,38(12):46-53.
[5]李逸驰,孙国强,杨义,等.含经VSC-HVDC并网海上风电场的交直流系统概率最优潮流[J].电力自动化设备,2015,35(9):136-142.LI Yichi,SUN Guoqiang,YANG Yi,et al.Probabilistic optimal power flow of AC/DC system with offshore wind farm connected to grid via VSC-HVDC [J].Electric Power Automation Equipment,2015,35(9):136-142.
[6]张里,刘俊勇,刘友波,等.计及风速相关性的电网静态安全风险评估[J].电力自动化设备,2015,35(4):84-89.ZHANG Li,LIU Junyong,LIU Youbo,et al.Static security risk assessment of power system considering wind speed correlation[J].Electric Power Automation Equipment,2015,35(4):84-89.
[7]朱星阳,黄宇峰,张建华,等.基于随机潮流的含风电电力系统静态安全评估[J].电力系统自动化,2014,38(20):46-53,60.ZHU Xingyang,HUANG Yufeng,ZHANG Jianhua,et al.Static security assessment based on probabilistic load flow for wind power integrated power systems[J].Automation of Electric Power Systems,2014,38(20):46-53,60.
[8]李智,韩学山,杨明,等.基于分位点回归的风电功率波动区间分析[J].电力系统自动化,2011,35(3):83-87.LI Zhi,HAN Xueshan,YANG Ming,et al.Wind power fluctuation intervalanalysis based on quantile regression [J].Automation of Electric Power Systems,2011,35(3):83-87.
[9]杨明,范澍,韩学山,等.基于分量稀疏贝叶斯学习的风电场输出功率概率预测方法[J].电力系统自动化,2012,36(14):125-130,142.YANG Ming,FAN Shu,HAN Xueshan,et al.Wind farm generation forecastbased on componentialsparse Bayesian learning [J].Automation of Electric Power Systems,2012,36 (14):125-130,142.
[10]KHOSRAVI A,NAHAVANDI S.Combined nonparametric prediction intervals for wind power generation[J].IEEE Transactions on Sustainable Energy,2013,4(4):849-856.
[11]周松林,茆美琴,苏建徽.风电功率短期预测及非参数区间估计[J].中国电机工程学报,2011,31(25):10-16.ZHOU Songlin,MAO Meiqin,SU Jianhui.Short-term forecasting of wind power and non-parametric confidence interval estimation[J].Proceedings of the CSEE,2011,31(25):10-16.
[12]SCOTT D W.Multivariate density estimation:theory practice and visualization wiley series in probability and mathematical statistics[M].New York,USA:John Wiley and Sons,1992.
[13]SEVLIAN R,RAJAGOPAL R.Detection and statistics of wind power ramps[J].IEEE Transactions on Power Systems,2013,28(4):3610-3620.
[14]FERREIRA C,GAMA J,MATIAS L,et al.A survey on wind power ramp forecasting[R].Illinois,America:Argonne National Laboratory(ANL),2011.
[15]AWS Truewind.AWS Truewind’s final report for the Alberta forecasting pilot project[EB/OL].[2015-03-02].http://www.aeso.ca/downloads/Alberta_PP_Final_Report_AWST_Jun25.pdf.
[16]何成明,王洪涛,王春义,等.风电功率爬坡事件作用下考虑时序特性的系统风险评估[J].电力自动化设备,2016,36(1):35-41.HE Chengming,WANG Hongtao,WANG Chunyi,etal.Risk assessment considering time-sequence characteristics for power system with wind power ramp event[J].Electric Power Automation Equipment,2016,36(1):35-41.
[17]HWANG M Y,JIN C H,LEE Y K,et al.Prediction of wind power generation and power ramp rate with time series analysis[C]//Proceedingsof2011 3rd InternationalConference on Awareness Science and Technology.Dalian,China:[s.n.],2011:512-515.
[18]ZHENG H Y,KUSIAK A.Prediction of wind farm power ramp rates:a data-mining approach [J].JournalofSolar Energy Engineering,Transactions of the ASME,2009,131(3):111-118.
[19]GAN D,KE D P.Wind power ramp forecasting based on leastsquaresupportvectormachine[C]//2014 2nd International Conference on Energy Engineering and Environment Engineering.Hong Kong,China:[s.n.],2014:162-166.
[20]PINDORIYA N M,SINGH SN,SINGH SK.Anadaptive wavelet neural network-based energy price forecasting in electricity markets[J].IEEE Transactions on Power Systems,23(3):1423-1432.
[21]王贺,胡志坚,陈珍,等.基于集合经验模态分解和小波神经网络的短期风功率组合预测[J].电工技术学报,2013,28(9):137-144.WANG He,HU Zhijian,CHEN Zhen,et al.A hybrid model for wind powerforecastingbased on ensembleempiricalmode decomposition and wavelet neural networks[J].Transactions of China Electrotechnical Society,2013,28(9):137-144.
[22]KARNIOTAKIS G,STAVRAKAKIS G S,NOGARET E F.Wind power forecasting using advanced neural network models[J].IEEE Transactions on Energy Conversion,1996,11(4):762-767.
