特高压同塔双回线路故障测距算法
2016-05-23郝良霞徐玉琴
王 艳,郝良霞,徐玉琴
(华北电力大学 电气与电子工程学院,河北 保定 071003)
0 引言
同塔双回线路由于2回线路共用1个杆塔,具有所需出线走廊窄、占用良田少、建设速度快、经济效益显著等特点,因此在实际运行和规划建设中已大量应用,并将成为特高压输电的发展趋势。
特高压交流输电由于电压等级高、输送距离长、导线及杆塔结构变化,使得特高压电网的分布电容电流变大[1],分布电容在暂态过程中将引起各种高频自由振荡分量,幅值最大的高频分量的频率比超高压系统产生的高频分量更加接近工频,且通常是非整次谐波;线路时间常数大导致非周期分量衰减缓慢[2];双回线间的互感作用和存在跨线故障等因素,导致特高压故障电气特征发生了一定变化,给特高压同塔双回线路的故障测距带来了一定难度。传统的以集中参数线路模型得到的测距误差不能被现场接受,需要采用分布参数线路模型建模[1]。国内外的研究者对同塔双回输电线路的测距算法做了大量研究,取得了不少成果。现有的测距算法按原理可分为:基于工频量的故障测距法[3-4]、行波测距法[5-7]、人工智能测距法[8-10]和电压测距法。然而现有的基于工频量的故障测距方法不能直接应用于特高压同塔双回输电线路,需采用恰当的滤波算法提取工频分量来克服非常严重的暂态过程给故障测距带来的较大误差[11]。特高压同塔双回输电线路发生故障时暂态过程丰富,适合应用基于暂态行波信号的行波测距法,但需要配备专门的高速采样测量设备,硬件成本及二次侧改造成本较大。人工智能测距法目前还处于理论研究探索阶段,其实用化有待于进一步验证。电压测距法测距误差较大,没有在实际中得到应用。现有的测距算法按所需电气量信息的来源又可分为单端法[12-14]和双端法[15-17]。单端法实现简便,无需通信通道传送对端信息,但获取的信息量较少,受故障点过渡阻抗和对端系统运行参数的影响,定位精度不高。双端法从原理上消除了过渡阻抗和系统阻抗的影响,具有更高的精度。对出线较多的短线路,可以采用单端法以降低观测站设备复杂程度,提高可靠性;对出线少的长线路,则多使用精度较高的双端法。特高压同塔双回输电线路出线少、输送距离长,所以适合采用双端法。
本文采用将故障点作为已知、引入参考点与之匹配的思想,在此基础上构造双曲余弦双端测距函数,并提出一种利用测距函数幅值特性对特高压同塔双回线故障进行测距的新方法。其测距结果不受过渡电阻、分布电容、系统阻抗等因素的影响,测距速度快、精度高,适用于特高压同塔双回线路的整个故障期间。
1 特高压电网半波傅氏窄带滤波算法
电力系统保护与控制中,信号分析与处理多是基于正弦基波的。而特高压电网发生故障后,电压、电流信号含有衰减直流分量和各种谐波成分,需要进行滤波处理。文献[18]指出电网发生单相接地故障时,1000 kV系统的谐波含量明显高于500 kV系统,而且谐波成分中包含更多高次谐波,以3次、4次、6次、9次为主;相间故障时,1000 kV同塔双回输电线路中的谐波以3.5次、5.5次以及低于基波的非整次谐波为主。而传统的全波傅氏算法虽然可以完全滤除整次倍高次谐波,对非整次高频分量亦有一定的抑制作用,但不能滤除低于基波的非整次谐波和衰减非周期分量。差分全波傅氏算法能滤除直流分量和所有的整次谐波,但是对非整次谐波的抑制能力较弱。为此,本文从基波频率出发,利用零极点设置法,设计出一种适用于提取特高压电网基波信号的窄带数字滤波算法。
1.1 窄带滤波器
保留基波频率 50 Hz,ωp=2π×50=100π(rad/s),得极点 Ae±jωpTs;同时令幅频特性分别在低频 ωTs=0、高频 ωTs=π处截止,得零点ej0=1和ejπ=-1。 由z平面零-极点得到该窄带数字滤波器的传递函数为:
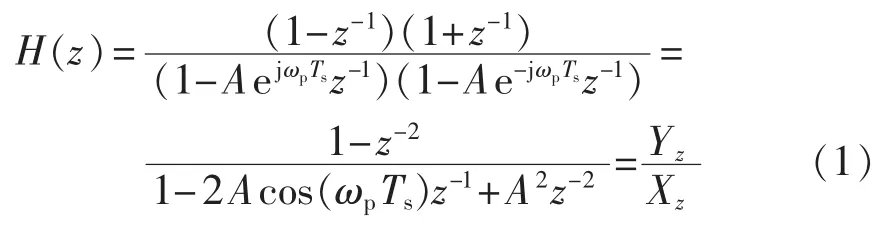
将窄带滤波器的传递函数转换为差分方程式:

其中,B1=2 Acos(ωpTs);B2=A2;A=2-cos(ΔωTs) -[cos2(ΔωTs)-4cos(ΔωTs)+3]1/2;Δω=2πΔf,Δf为幅值半值点处频率偏离值,由图1(a)可见,Δf越小,窄带滤波器滤波效果越好;Ts=0.02/N为采样间隔,N为每周期采样点数。
图1(b)为 Δf取 5 Hz、采样频率为 4.8 kHz时频率响应特性,其中K是50 Hz对应的幅值。K随Δf与采样频率变化而变化,当Δf与采样频率确定时,窄带滤波器的幅频响应特性确定,K值取值即是该幅频特性下基频所对应的幅值。由图1(b)可见该窄带滤波器能够完全滤除直流分量,对非整次低频分量和各高次谐波均有较好的抑制作用。
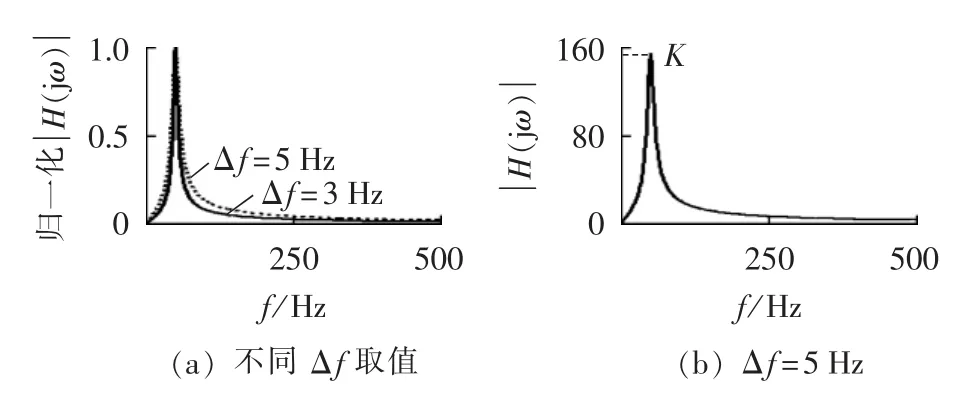
图1 频率响应特性曲线Fig.1 Frequency response characteristic curves
1.2 窄带滤波器的响应时间
由式(2)知窄带滤波器的滤波过程是一个递推计算的过程,方程的求解需用初值来启动,响应时延不确定。 当 y(1)=y(2)=0 时,窄带滤波器的响应时间如图 2(a)所示;当 y(1)和 y(2)的值越接近输出的稳定值,滤波的响应时延就越短。由此可见,要缩短窄带滤波器的响应时间,对差分方程求解初值的计算至关重要。
半波傅氏算法可以完全滤除奇次倍高次谐波,对非整次高频谐波有抑制作用,在故障后10 ms即可进行计算,相对于全波傅氏算法的时延减少了半个周期。由半波傅氏算法的实虚部幅频特性可知,实部计算对低频分量的抑制效果较好,受衰减非周期分量影响很小,并且当输入信号为基频信号x1(t)=cos(ωpt+φ)或 x2(t)=sin(ωpt+φ)时,半波傅氏算法实部计算结果正好等于输入信号初值,因此,半波傅氏算法实部计算能够较为准确地给出窄带滤波算法的计算初值。但应该注意的是,需要根据窄带滤波器幅频特性曲线对通带中心频率50 Hz的放大系数K,对初值进行幅值调整。故本文采用半波傅氏算法的2个数据窗计算得到2个基波分量的实部Re1和Re2,令 y(1)=KRe1,y(2)=KRe2,从 y(3)开始,采用式(2)的差分方程,由此实现的滤波算法的响应时间见图2(b)。这种算法的数据窗仅为基波半个周期加上1个采样间隔Ts。滤波输出在略超过10 ms时就趋于稳定,响应时延较图2(a)大幅减少。
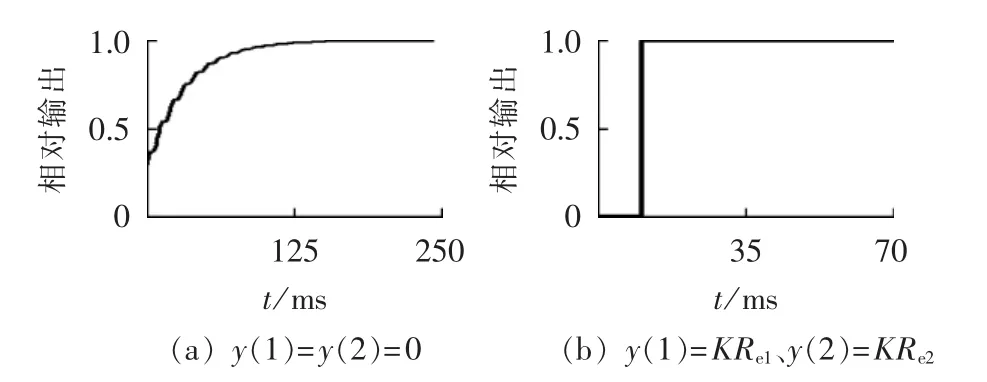
图2 滤波器响应时间Fig.2 Response time of filters
2 特高压同塔双回线路故障测距原理
2.1 构造测距函数
特高压同塔双回线路存在相间互感与线间互感,耦合效应严重,故先利用六序分量法对线路两端电气量进行解耦,可得6个独立的序分量。
图3为同塔双回线路同正序故障分量序网图。由于特高压同塔双回线路输电距离长、分布电容大,故采用分布参数线路模型,其线路阻抗与故障距离呈双曲正切函数关系,如式(3)所示。

其中,IMfT1为由M侧母线流向故障点的同正序电流故障分量;UfT1为故障点f处同正序电压故障分量;γT1、ZcT1分别为同塔双回线同正序传播常数、波阻抗;lMf为f点到M侧距离;lM为由M侧同正序系统等值阻抗2Z1sM决定的虚拟等值线路长度,其与2Z1sM的函数关系为 lM=atanh(2Z1sM/ZcT1) /γT1。

图3 同正序故障分量序网图Fig.3 Homotopic positive-sequence fault component network
同理可得:

其中,INfT1为由N侧母线流向故障点的同正序电流故障分量;lMN为N侧到M侧距离;lN为由N侧同正序系统等值阻抗2Z1sN决定的虚拟等值线路长度,其与 2Z1sN的函数关系为 lN=atanh(2Z1sN/ZcT1) /γT1。
由式(3)和式(4)可得:
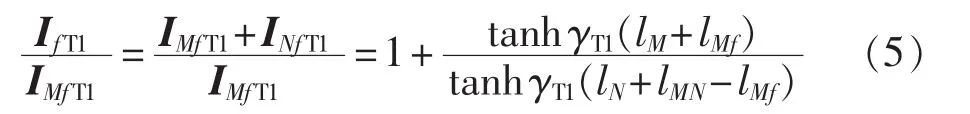
其中,IfT1为流入故障点的同正序电流故障分量。
另根据图3的长线电报方程得:
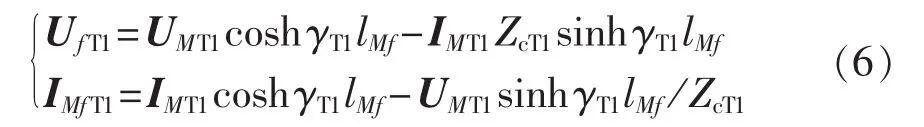
其中,UMT1、IMT1分别为M侧保护测量到的同正序电压、电流故障分量。将UMT1=-IMT1ZcT1tanhγT1lM代入式(6)得:

将式(5)、式(7)左右相乘得:
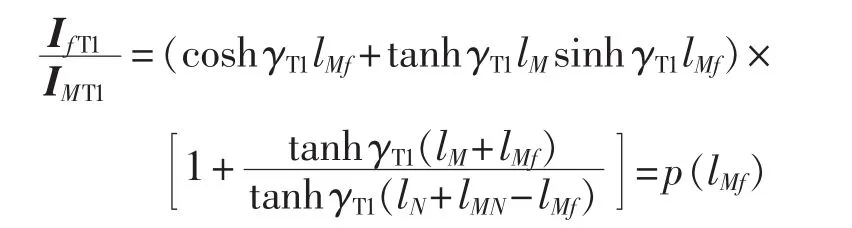
即:

其中,p(lMf)为同正序电流故障分量分配系数。
当故障发生后,故障位置客观上是存在但未知的。为了找到故障位置,引入一参考点d,其等值序网络如图4所示。
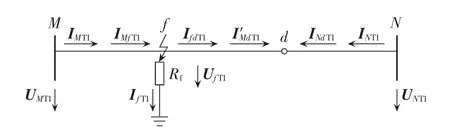
图4 同塔双回线路同正序等值序网图Fig.4 Homotopic positive-sequence equivalent model of double-circuit lines on same tower
由图4知:

由长线电报方程可得参考点d的同正序电流计算值式(10)和实际值式(11):

其中,IMdT1、INdT1分别为根据长线方程由M、N侧同正序量推算出的d点两侧的同正序电流量;I′MdT1为M侧流向d点的实际同正序电流量;lfd为f点到d点距离,lfd=lMd-lMf。
联立式(6)、(9)、(10)、(11)得:
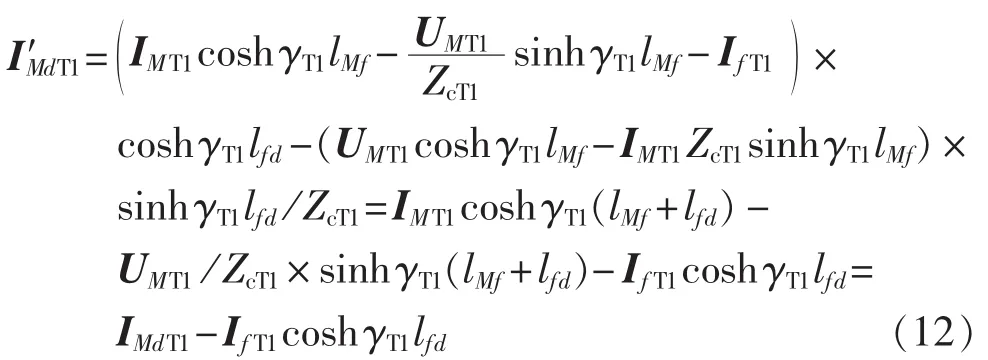
在d点又有:

将式(12)代入式(13),整理得:

同理,当f点位于d点右侧时式(14)仍成立。
将式(8)与式(14)等式两侧对应相除得到一构造函数g(lMd)即为特高压同塔双回线路的测距函数,见式(15)。
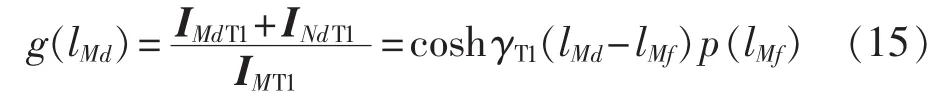
2.2 故障测距方法
对于特高压同塔双回线路,当发生故障后,故障点位置f保持不变,即lMf不变。当同塔双回线路参数且系统阻抗给定时,p(lMf)为一定值,测距函数g(lMd)幅值大小取决于双曲余弦函数 coshγT1(lMd-lMf)的幅值特性。而双曲余弦函数是偶函数,存在最大值点。由双曲余弦函数幅值特性可知,当lMf=lMd,即参考点d与故障点f重合时,其幅值最大。利用双曲余弦函数的这个特性即可进行故障点定位。
具体故障测距方法如下:
a.利用半波傅氏窄带滤波算法提取特高压同塔双回线路两端保护安装处的电压、电流基波分量,进行六序解耦后得线路两端的同正序基波电压、电流故障分量;
b.令lMd=0,以步长ΔS=1 km逐次递增,依次计算测距函数g(lMd)幅值,直至被保护线路全长;
c.搜索测距函数幅值最大点,即为故障点,该点至线路保护安装处的距离为故障距离。
lMd取值从线路出口处开始,根据测距精度的需要,步长ΔS可以取1 km,甚至更小;步长ΔS取值越小,测距精度越高,但是计算量将剧增,因此实际应用时ΔS的取值应综合考虑计算速度和测距精度。实际应用中,为了实现长线路的快速准确测距,需要同时兼顾计算速度和测距精度,可采用如下变步长的方法来达成:测距函数g(lMd)关于lMd=lMf偶对称且在lMd=lMf时取得最大幅值,当参考点d位于故障点f左侧时,测距函数幅值随着lMd的增大呈现增大的趋势,而当参考点d位于故障点f右侧时,测距函数幅值随着lMd的增大呈现减小的趋势。基于此,首先lMd以较大步长ΔS1(如ΔS1=50 km),依次计算测距函数g(lMd)幅值,将故障点锁定在测距函数最大和次大(或2个最大)幅值对应的2个相邻点间,此时线路故障范围长度缩短到ΔS1;然后在该故障范围内将搜索步长缩小为ΔS2(如ΔS2=10 km),再对锁定的线路范围重复以上步骤直到所得线路区间长度小于某一给定值;最后根据实际的线路长短和精度要求确定该区间步长 ΔSn(ΔSn为 1 km、0.5 km 或 0.1 km),计算该区间内各点处测距函数幅值,幅值最大点至线路保护安装处的距离即为测距结果。
3 对测距原理的分析
对测距原理的分析结果如下。
a.不受分布电容电流影响。基于分布参数模型,将特高压同塔双回线路参数物理特性准确地呈现于模型中,因此不受分布电容电流的影响。
b.不受系统阻抗影响。当特高压同塔双回线路参数与系统阻抗给定时,p(lMf)为一定值,不影响测距结果。而故障发生后,随着时间的推移,运行方式可能发生变化,但该过程是一个缓慢过程,而本文所提方法测距快速,即在故障发生的短暂时间内系统运行方式认为不变,因此该测距方法基本不受系统阻抗的影响。
c.不受过渡电阻影响。本文所提方法利用测距函数幅值最大特性进行故障定位,该特性原理上与过渡电阻无关,因此不受过渡电阻的影响。
d.不受故障类型影响。同正序基波分量在特高压同塔双回线路任何故障类型中都存在,因此该方法不受故障类型的影响,对特高压同塔双回线路各种故障都可用其进行准确测距,且适用于同塔双回线故障后的整个故障期间。
e.不受负荷电流影响。由于采用线路两端同正序基波故障分量进行测距,理论上与负荷电流无关,基本不受负荷电流的影响。
f.不受线路上固有高抗影响。超、特高压输电线路对地电容大,为了补偿线路的容性充电功率、控制无功潮流、稳定网络运行电压、限制潜供电流等,一般要安装并联电抗器。对于线路一端或两端装有并联电抗器的系统,上文推导过程中的IMT1、INT1分别为M、N侧并联电抗器安装出口处的同正序电流故障分量,lM(lN)为由 M(N)侧同正序系统等值阻抗2Z1sM(2Z1sN)与并联电抗器同正序电抗并联后的总阻抗对应的虚拟等值线路长度。当线路中间接有并联电抗器时,由于实际系统中并联电抗器安装位置是确定的,可以利用长线方程求出并联电抗器安装处的电气量,后将并联电抗器安装处等效为线路一端,再应用本文测距原理进行测距。
4 仿真验证
本文利用MATLAB搭建一电压等级为1000kV、长为600 km的同塔双回线路系统模型。线路参数借鉴皖南—浙北线路参数[19]:r1=0.00819277 Ω /km,x1=0.254 819 28 Ω /km,c1=0.014 698 80 μF /km;r0=0.159 036 14 Ω /km,x0=0.896 987 95 Ω /km,c0=0.008 07229 μF /km;rm=0.15530120 Ω /km,xm=0.56265060 Ω /km,cm=0.00259036 μF /km。
同塔双回线路故障分为接地故障和不接地故障,其类型如表1所示。本文分别对表1中22种故障类型进行测距仿真,其相对测距误差的计算公式为:。
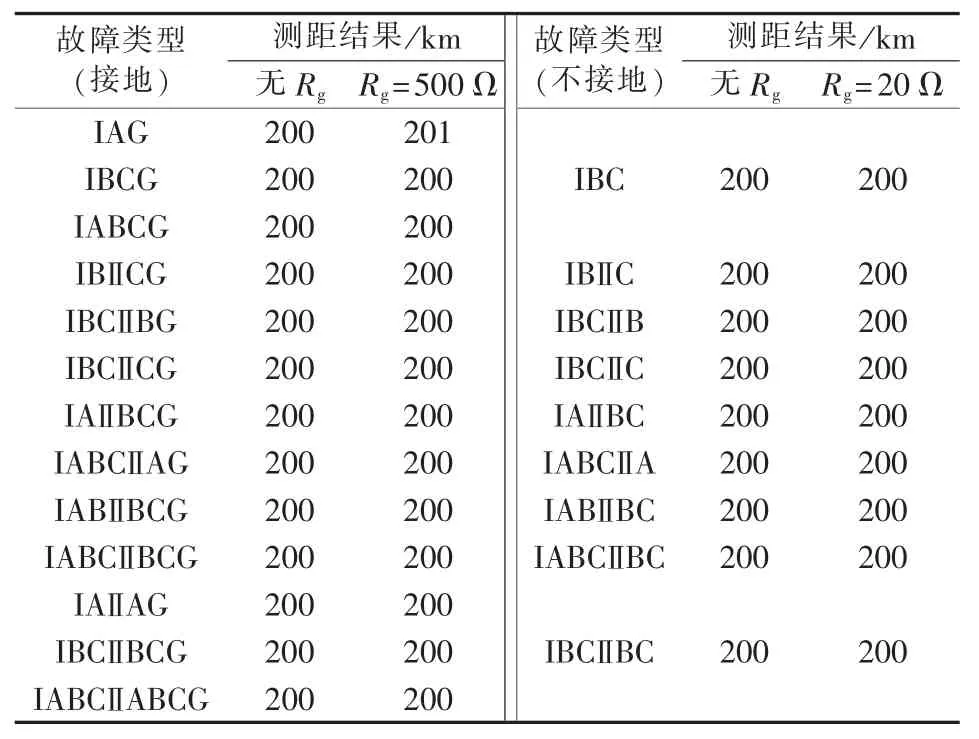
表1 过渡电阻对不同故障类型测距的影响Table1 Influence of transition resistance on fault location for different fault types
表1是特高压同塔双回线路在200 km处发生各种类型故障时(ΔS取1 km时)的测距结果。由表1可知,故障发生在距线路首端200 km处时,本文所提测距方法不受故障类型及过渡电阻Rg影响,具有很高的测距精度。
表2是特高压同塔双回线路在不同位置处发生故障时(ΔS取1 km时)的测距结果。由表2可知,本文所提测距方法不受故障位置影响,具有很高的测距精度。
由于同塔双回线故障种类众多,而文章篇幅有限,现只给出几种故障情况下,测距结果随故障位置、过渡电阻、负荷电流变化的测距误差。
图5、图6分别将故障位置和过渡电阻对IAG、IABⅡBC故障测距结果的影响清楚地呈现于三维图中。由图5、图6可见该故障测距方法受故障位置、过渡电阻和故障类型的影响很小,满足测距精度的要求。

表2 故障位置对不同故障类型测距的影响Table2 Influence of fault position on fault location for different fault types
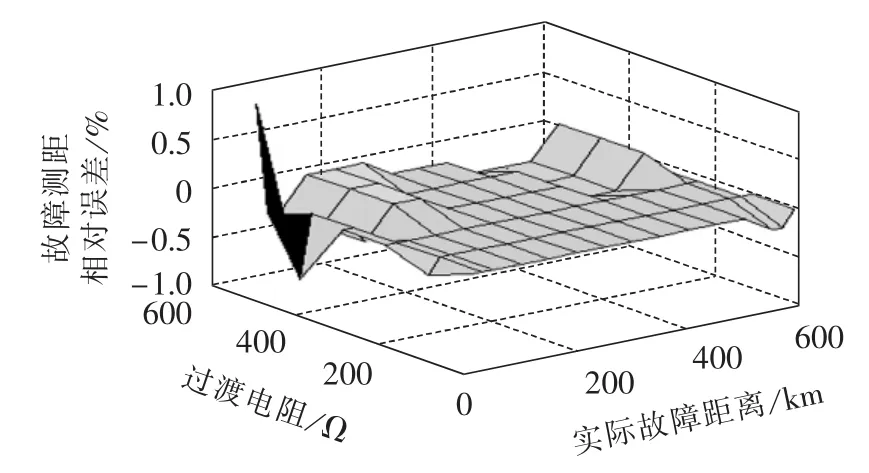
图5 故障位置和过渡电阻对IAG故障测距结果的影响Fig.5 Influence of fault position and transition resistance on IAG fault location
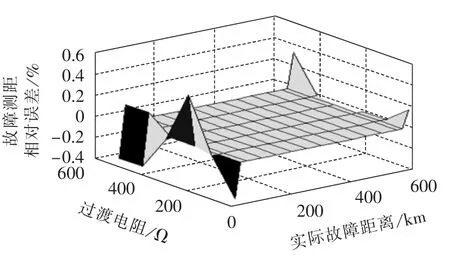
图6 故障位置和过渡电阻对IABⅡBC故障测距结果的影响Fig.6 Influence of fault position and transition resistance on IABⅡBC fault location
图7绘出了故障位置和负荷电流对IBⅡC故障测距结果的影响状况,可见该故障测距方法受故障位置和负荷电流的影响很小,满足测距精度的要求。图8呈现了过渡电阻和负荷电流对IBCⅡBCG 495 km处故障测距结果的影响。由图8可见该故障测距方法不受过渡电阻和负荷电流的影响,具有很高的测距精度。
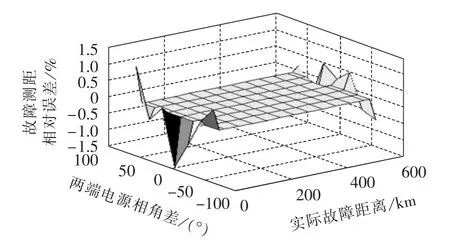
图7 故障位置和负荷电流对IBⅡC故障测距结果的影响Fig.7 Influence of fault position and load current on IBⅡC fault location

图8 过渡电阻和负荷电流对IBCⅡBCG 495 km处故障测距结果的影响Fig.8 Influence of transition resistance and load current on location of IBCⅡBCG 495 km fault
为了分析本文算法的测距性能,表3在实际故障距离为 20 km、120 km、300 km、420 km、510 km 情况下对本文算法与特高压工频测量阻抗法[20]的测距结果进行对比分析,表3中已将文献[20]中的测量阻抗值相应地换算为测量距离。比较两者的测距结果可知:文献[20]所提工频阻抗法在无过渡电阻或过渡电阻较小时能够实现准确测距,在过渡电阻较大或者线路近端故障时测距误差较大;而本文的测距算法基本不受过渡电阻和故障位置的影响,能够实现精确测距。

表3 工频阻抗法和本文方法故障测距结果Table 3 Results of fault location by power-frequency impedance algorithm and proposed algorithm
5 结语
在分布参数模型基础上,本文提出了一种特高压同塔双回线路故障测距新算法,原理上避免了分布电容电流对故障测距的影响。此算法是基于测距函数幅值特性提出的,由双曲余弦函数幅值特性可知,当且仅当所取参考点与故障点匹配时,测距函数的幅值最大,因此,本文测距方法在原理上不存在伪根。测距结果受过渡电阻、系统阻抗、故障类型、故障位置和负荷电流等因素的影响很小,具有很高的测距精度,能够满足现场应用的要求。
参考文献:
[1]王宾,董新洲,薄志谦,等.特高压长线路单端阻抗法单相接地故障测距[J].电力系统自动化,2008,32(14):25-29.WANG Bin,DONG Xinzhou,BO Zhiqian,et al.An impedance fault location algorithm for UHV long transmission lines with single-line-to-ground faults[J].Automation of Electric Power Systems,2008,32(14):25-29.
[2]王伟,余锐,陈愚,等.特高压输电线路保护故障测距的应用研究[J].电力系统保护与控制,2013,41(19):40-46.WANG Wei,YU Rui,CHEN Yu,et al.Application research of fault location of UHV transmission line protection[J].Power System Protection and Control,2013,41(19):40-46.
[3]宋国兵,索南加乐,许庆强,等.基于双回线环流的时域法故障定位[J].中国电机工程学报,2004,24(3):24-29.SONG Guobing,SUONAN Jiale,XU Qingqiang,et al.A novel time-domain algorithm for locating faults on parallel transmission lines by circulating current[J].Proceedings of the CSEE,2004,24(3):24-29.
[4]索南加乐,吴亚萍,宋国兵,等.基于分布参数的同杆双回线单线故障准确测距原理[J].中国电机工程学报,2003,23(5):39-43.SUONAN Jiale,WU Yaping,SONG Guobing,et al.New accurate fault location algorithm for parallel lines on the same tower based on distribute parameter[J].Proceedings of the CSEE,2003,23(5):39-43.
[5]徐高,龚庆武,李勋,等.基于原子分解和行波自然频率的单端故障测距方法[J].电力自动化设备,2014,34(5):133-138.XU Gao,GONG Qingwu,LIXun,etal.Single-terminalfault location based on atomic decomposition and natural frequency of traveling wave[J].Electric Power Automation Equipment,2014,34(5):133-138.
[6]覃剑,黄震,邱宇峰,等.基于小波变换的同杆并架双回线双端行波故障测距[J].电力系统自动化,2004,28(5):51-55.QIN Jian,HUANG Zhen,QIU Yufeng,et al.Wavelet transform based double terminal method of traveling wave fault location in double-circuit parallel transmission line[J].Automation of Electric Power Systems,2004,28(5):51-55.
[7]邬林勇,何正友,钱清泉.一种提取行波自然频率的单端故障测距方法[J].中国电机工程学报,2008,28(10):69-75.WU Linyong,HE Zhengyou,QIAN Qingquan.A singleended fault location method using traveling wave natural frequency[J].Proceedings of the CSEE,2008,28(10):69-75.
[8]郭付军,林军.用多个对应的后向神经网络进行同杆双回线故障识别及测距的模式[J].电网技术,2002,26(10):14-17.GUO Fujun,LIN Jun.Iden tification and location of fault on double circuit tower by multi-corresponding BP ANN method[J].Power System Technology,2002,26(10):14-17.
[9]毛鹏,孙雅明,张兆宁.基于神经网络原理的高压架空输电线路故障测距模型的研究[J].电力系统及其自动化学报,1999,11(3):66-73.MAO Peng,SUN Yaming,ZHANG Zhaoning.The model study of fault location system for high voltage overhead transmission line based on hierarchical distributed nerual networks[J].Proceedings of the CSU-EPSA,1999,11(3):66-73.
[10]余晓丹,刘众仆,王钢,等.应用模糊神经网络实现故障测距[J].中国电力,1998,31(3):10-13.YU Xiaodan,LIU Zhongpu,WANG Gang,et al.Application of fuzzy neural network on fault location[J].Electric Power,1998,31(3):10-13.
[11]薛士敏,贺家李,李永丽.特高压输电线路负序方向纵联保护[J].电力系统自动化,2007,31(18):50-53.XUE Shimin,HE Jiali,LI Yongli.Pilot protection of ultra-highvoltage transmission lines with negative sequence directional comparison[J].Automation of Electric Power Systems,2007,31(18):50-53.
[12]许飞,董新洲,王宾,等.新型输电线路单端电气量组合故障测距方法及其试验研究[J].电力自动化设备,2014,34(4):37-42.XU Fei,DONG Xinzhou,WANG Bin,et al.A novel fault location algorithm of single terminal electric quantity combination for transmission lines[J].Electric Power Automation Equipment,2014,34(4):37-42.
[13]粟小华.基于平行双回线单端实时数据的准确故障测距实用新方法[J].继电器,2001,29(5):5-7.SU Xiaohua.A new and practical method for fault location based on single-end real time data in paralleled double circuit line[J].Relay,2001,29(5):5-7.
[14]束洪春,刘振松,彭仕欣.同塔双回线电弧故障单端测距算法[J].电力自动化设备,2008,28(12):11-14.SHU Hongchun,LIU Zhensong,PENG Shixin.Single terminal arc fault location for two parallel transmission lines on same tower[J].Electric Power Automation Equipment,2008,28(12):11-14.
[15]索南加乐,宋国兵,许庆强,等.利用两端非同步电流的同杆双回线故障定位研究[J].中国电机工程学报,2004,19(8):99-106.SUONAN Jiale,SONG Guobing,XU Qingqiang,etal.Fault location algorithms for parallel transmission lines using two terminals nonsynchronized current data[J].Proceedings of the CSEE,2004,19(8):99-106.
[16]夏经德,张向聪,黄新波,等.基于纵向阻抗的双端量故障测距新算法[J].电力自动化设备,2015,35(10):133-139.XIA Jingde,ZHANG Xiangcong,HUANG Xinbo,etal.Fault locating based on longitudinal impedance according to dualterminal variables[J].Electric Power Automation Equipment,2015,35(10):133-139.
[17]张金虎,徐振宇,杨奇逊.基于双端量的串联补偿线路单相接地故障测距算法[J].电力自动化设备,2015,35(4):121-125.ZHANG Jinhu,XU Zhenyu,YANG Qixun.Single-phase grounding faultlocation algorithm based on dualterminal variables for line with series compensation [J].Electric Power Automation Equipment,2015,35(4):121-125.
[18]刘振亚.特高压交流输电技术研究成果专辑[M].2009版.北京:中国电力出版社,2011:73-74.
[19]周春霞,余越,赵寒,等.特高压同塔双回线路零序电流补偿系数整定对接地距离保护的影响研究[J].电网技术,2012,36(12):106-111.ZHOU Chunxia,YU Yue,ZHAO Han,et al.Influence of zerosequence current compensation coefficient setting on earth-fault distance protection fordouble circuitUHVAC transmission lines on the same tower[J].Power System Technology,2012,36(12):106-111.
[20]焦彦军,侯仰栋,章政杰,等.基于分布参数的特高压交流双回长线路距离保护[J].电网技术,2008,32(2):119-123.JIAO Yanjun,HOU Yangdong,ZHANG Zhengjie,et al.Distance protection of UHV AC double-circuit long transmission line based on distributed parameters[J].Power System Technology,2008,32(2):119-123.
