基于拉丁超立方采样技术的半不变量法随机潮流计算

黄 煜，徐青山 ，卞海红，刘建坤

（1.东南大学 电气工程学院，江苏 南京 210096；2.南京工程学院 电力工程学院，江苏 南京 211167；3.江苏省电力公司电力科学研究院，江苏 南京 210003）

0 引言

新能源发电作为解决能源危机和环境污染等问题的有效手段，近年来在我国得到了大力发展。由于可再生能源发电（如风电、太阳能光伏发电等）具有很大的不确定性，再加上分布式电源、负荷及源荷之间的关联影响，未来电网将呈现复杂的高维随机特性，给系统运行控制、优化调度带来更大的挑战。因此，加快建立适应新环境的电网分析和评估方法具有重要意义［1-2］。

潮流计算是电力系统运行分析和规划设计的基础。常规潮流往往难以全面反映系统中不确定因素的影响；而随机潮流通过概率统计的方法得到系统稳态运行的宏观统计信息［3］，是解决这一问题的重要工具。在其基础上应用自回归滑动平均（ARMA）模型和时移技术［4-5］、Copula函数或者基于相关系数矩阵的Cholesky分解等方法可以处理随机变量间的相关性问题，以适应未来新环境下电网运行分析的特点及需求。

目前，随机潮流的计算方法大致可分为3类：模拟法、近似法和解析法。模拟法在保证样本规模足够大的情况下能够获得很高的精度，且原理简单、适用性广。但其最大的缺点是耗时巨大，无法对规模庞大的系统进行在线潮流计算。文献［6］通过K均值聚类的方法对不同时段的样本点合并聚类，能够有效地减小计算规模。文献［7］改进了相应的采样技术，在不影响精度的情况下，大幅减少了样本的数量。尽管上述方法可以显著缩短模拟法的耗时，但仍无法从根本上解决问题。近似法是利用随机变量的数字特征（如期望、方差、原点矩等）来近似描述所求状态量的统计特性，常见的包括一次二阶矩法（FOSMM）、点估计法（PEM）［8］等。 这类方法计算速度较快，但当考虑输入变量相关性时，计算会非常复杂且高阶矩的误差较大。解析法先将非线性潮流方程简化处理，得到随机变量间的线性关系，再用卷积运算求得状态量的概率分布，整个过程只需一次计算就能快速得到结果。为了避免复杂的常规卷积运算，可以采用文献［9］中的快速傅里叶变换（FFT）或者半不变量法［10-13］。解析法最大的问题在于各输入变量之间必须保证相互独立，这与电网的实际情况不符；而且简化后的潮流模型会对计算精度造成一定的影响。

本文提出一种可考虑输入变量相关性的基于拉丁超立方采样技术的半不变量法CM-LHS（Cumulant Method based on Latin Hypercube Sampling）计算随机潮流。通过拉丁超立方采样和Nataf变换得到具有相关性的输入变量的随机序列，结合半不变量和原点矩的关系计算其半不变量，以解决复杂输入变量的半不变量难以用数值方法求解的问题。利用Cholesky分解使输入变量之间满足线性独立的前提，并引入分段线性化潮流模型以减小计算误差。对IEEE 30和IEEE 118节点测试系统的仿真结果进行分析，验证了所提方法的准确性、快速性和实用性。

1 计及相关性的输入变量样本的产生

1.1 拉丁超立方采样

拉丁超立方采样（LHS）本质上是一种分层采样，其目的是使样本点均匀分布并覆盖整个采样空间［14］。LHS自1979年由M.D.Mckay等学者提出以来，现已广泛应用于多个领域。与简单随机采样相比，其优势如下：①为覆盖同样大小的样本空间，LHS的采样规模更小；②LHS的稳健性更好。传统的LHS方法主要分为采样和排序2步。

a.采样。设有 n 个输入随机变量 X1、X2、…、Xn，采样规模为N，其中任意一个随机变量Xk的累积分布函数为：

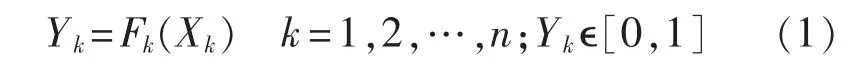
将Yk的取值区间N等分并取各区间中点作为Yk的采样值，则Xk的第l个采样值可由反函数得到。

将每个随机变量的N个采样值排成一行，形成n×N阶的初始采样矩阵S。

b.排序。排序是为了降低相互独立的随机变量样本之间的相关性影响，一般用Gram-Schmidt序列正交化的方法［7］将初始采样矩阵S的元素重新排列，使样本间的相关性趋于最小，但其只适用于随机变量相互独立的情况。

1.2 Nataf变换和相关性处理

LHS是实现单一随机变量采样的有效方法，但对于有多个随机变量的情况，需要先进行相关性分析。理论上，随机变量之间的关联影响可用联合分布函数完整、唯一地描述。但实际工程中，往往已知的是各随机变量的边缘分布，它们之间的联合概率分布却较难拟合。而Nataf变换以随机变量的边缘分布和相关系数矩阵为基本信息，结合Nataf分布理论［15-16］和 Cholesky 分解［17-18］的线性变换，可实现关联非正态随机变量和独立标准正态随机变量之间的转换，从而避开了正面求解联合概率分布的困难。

设 RX= ［ρij］为输入随机变量 X1、X2、…、Xn的相关系数矩阵，ρij为随机变量Xi和Xj的相关系数，表达式为：

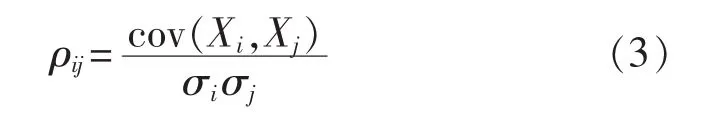
其中，σi、σj分别为随机变量 Xi、Xj的标准差。

由等概率边缘变换引入标准正态随机变量Z1、Z2、…、Zn，其相关系数矩阵 RZ= ［ρ′ij］。

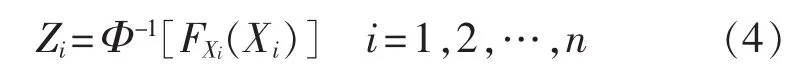
其中，Φ（·）为标准正态分布的累积分布函数。ρij和 ρ′ij具有如下的经验公式：

其中，变系数 F（ρij）取决于 Xi、Xj的分布，具体计算式可参考文献［19］。

在确定了相关系数矩阵后，对其进行Cholesky分解，即RZ=LLT，其中L为下三角矩阵。若标准正态随机向量满足：

其中，Y=［y1，y2，…，yn］T为独立标准正态随机向量。则可以证明［15］，Z*的相关系数矩阵为 RZ。 对 Z*采样得到样本矩阵（N 为样本数），定义的顺序矩阵为LS（LS为与相对应的n×N阶矩阵，每一行为从整数1到N的一个排列，对应着中相应行的元素的大小顺序）。设n个输入随机变量X1、X2、…、Xn通过LHS形成的样本矩阵为X*=按顺序矩阵LS重新排列，得到最终样本矩阵S′。若为任意无穷小量）［20］，意味着S′与原样本矩阵 X非常接近，即S′的相关系数矩阵近似为RX。

上述方法综合了LHS的优点并利用Nataf变换处理相关性，能够快速有效地产生计及相关性的输入随机变量的样本，为后续半不变量法随机潮流计算奠定基础。

2 半不变量法随机潮流计算

2.1 分段线性化潮流模型

非线性潮流方程包括节点注入功率方程和支路潮流方程，采用交流线性化模型，将其在基准运行点处进行泰勒展开并忽略2阶及以上的高次项，整理得：

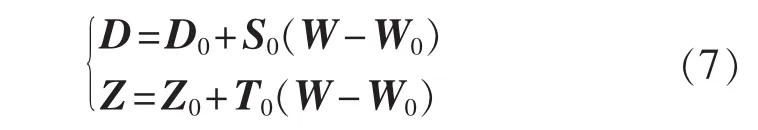
其中，W为节点注入功率向量；D和Z分别为状态向量（电压幅值和相角）和支路潮流向量（支路有功和无功）；下标0表示基准运行点（期望值）；S0和T0为灵敏度矩阵其中J0为雅可比矩阵，G0=（∂Z /∂D）|D=D0。

由于新能源的大规模接入以及系统关联性和复杂度的增长，输入变量的变化范围通常很大，采用单点线性化模型会引起较大的截断误差［21-23］。因此，在其基础上，引入潮流方程的分段线性化模型。

设Ptot为系统总的有功功率，有：

其中，NL为PQ节点个数；Pi为节点i的负荷有功；NG为PV节点个数为接入节点j的发电机输出的有功功率。

由于负荷功率和新能源出力均为随机变量，可知Ptot也是随机变量，其概率密度函数（PDF）可根据式（8）得到。图1大致给出了Ptot的PDF曲线，将其等间距地划分为T个区域，T一般取6～8。图1中μ为总有功功率的期望（均值）。

图1 总有功功率的PDF曲线Fig.1 PDF of total active power

在每个区域内选取相应的基准运行点，并将潮流方程在各点处分别线性化：

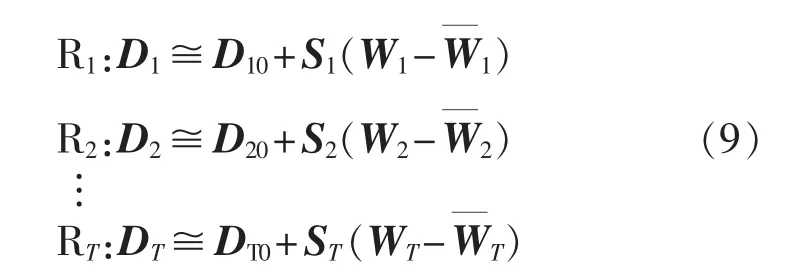
其中，Si为区域 Ri（i=1，2，…，T）对应的灵敏度矩阵；为区域 Ri的基准功率向量。的求解步骤如下：

a.由第1节中介绍的LHS方法产生输入随机变量的样本矩阵 Sn×N；

b.根据式（8）计算各样本向量［wj1，wj2，…，wjn］T（j=1，2，…，N）的 Ptot，并判断其所对应的区域；

c.将属于同一区域的样本取平均值，即得到区域 Ri的基准功率向量

将代入式（10）的节点功率方程，即可以得到区域Ri的基准运行点向量Di0。

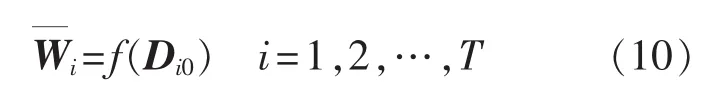
2.2 输入变量的半不变量求取

若已知输入变量的概率分布，采用常规数值方法对其进行数学推导可求得半不变量的解析式。对于服从正态分布或离散分布的随机变量，该方法能准确高效地得到其半不变量。然而对于分布函数较为复杂甚至未知的输入变量，其半不变量解析式难以推导，因此提出一种基于LHS的方法来计算其半不变量。

在输入变量X分布已知的情况下，根据其分布函数由 LHS 技术得到 N 个样本｛xs1，xs2，…，xsN｝，分别计算每个样本的各阶原点矩αv：

再由半不变量和原点矩的关系［24］，求出其各阶半不变量 γv：

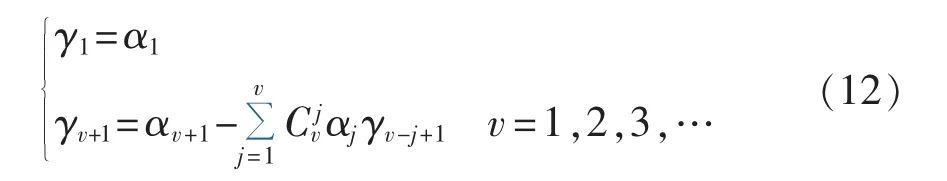
其中为组合数。一般取前7阶半不变量就能保证较高的计算精度。

当输入变量X分布函数未知时，可以根据其实测离散历史数据，利用经验分布函数u=Fe（X）和LHS技术求解半不变量，主要步骤如下。

a.对输入变量 X的离散历史数据 X=［x1，x2，…，xn］按从小到大的顺序进行排列，得到新的样本向量

b.通过式（13）得到输入变量X的经验分布函数 u=Fe（X）：

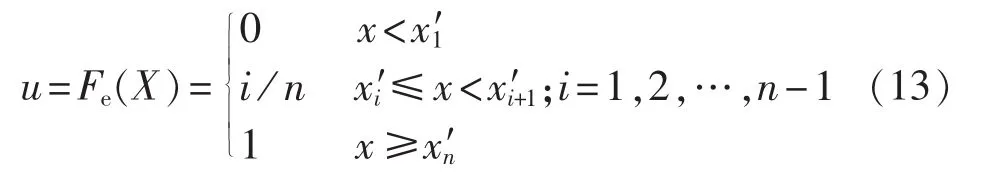
c.由X的经验分布采用LHS技术得到最终的样本向量［xs1，xs2，…，xsN］，再通过式（11）、（12）计算其各阶半不变量。

2.3 考虑输入变量相关性的半不变量计算

为了简化分析，先不考虑各节点注入功率之间的相关性，则节点i注入功率的随机变量ΔWi可表示为：

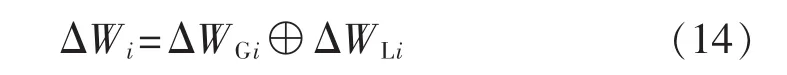
其中，“⊕”表示卷积运算；ΔWGi和ΔWLi分别为节点i的发电机功率和负荷功率的随机变量。

利用半不变量的齐次性和可加性［25］，将式（14）的卷积运算转换为半不变量的代数运算，可以大幅减少计算量。节点i注入功率的k阶半不变量为：

假设采用单点线性化的潮流模型，由式（7）可以推算得到状态变量ΔD与支路潮流ΔZ的各阶半不变量：

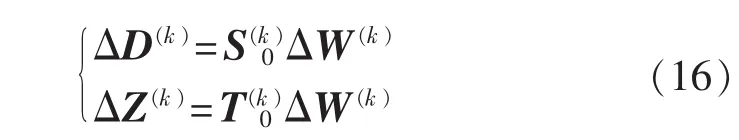
其中分别为矩阵S0和T0中各元素的k次幂所构成的矩阵。

半不变量法中独立性的前提条件是由卷积的性质所决定的，若要计及各节点注入功率的相关性，必须先将其表示为不相关的随机变量的线性组合。

设随机向量 Y=［y1，y2，…，yn］T满足：

其中，W为具有相关性的节点注入功率向量；G为其相关系数矩阵RWCholesky分解后的下三角矩阵。可以证明 y1、y2、…、yn为不相关的随机变量：

通过式（17）可以将具有相关性的输入变量W表示为不相关的随机变量Y的线性组合：

根据式（19），求得不相关变量Y的k阶半不变量 ΔY（k）。 在其基础上修正式（16），可得：

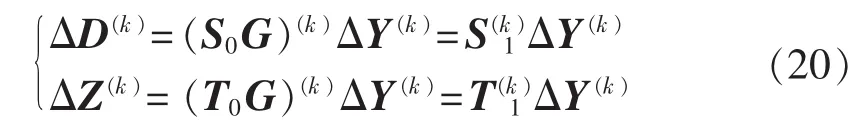
对于本文采用的分段线性化模型，不同的输入样本向量Wi所对应的灵敏度矩阵Si0、Ti0也不同，导致式（20）中的齐次关系被破坏了。针对这一难题，文献［26］通过半不变量的定义，详细推导出了分段线性函数因变量的半不变量与自变量分布之间的定量关系。再结合半不变量的可加性，可以求得潮流方程分段线性化后状态变量ΔD和支路潮流ΔZ的各阶半不变量。

2.4 Cornish-Fisher级数展开

当已知待求输出变量的半不变量后，通过级数展开的方法可以计算其概率分布，主要有Gram-Charlier级数、Edgeworth 级数、Cornish-Fisher级数等。与前2种级数相比，Cornish-Fisher级数在拟合非正态分布变量的概率分布时具有较好的收敛性和更高的精度。因此，本文采用Cornish-Fisher级数展开的方法。设α为待求输出变量z的分位数，则 z（α）为：

其中，z（α）=F-1（α）；ξ（α）=Φ-1（α）；γz，k为输出变量 z的k阶半不变量。由式（21）可直接计算出待求输出变量 z的累积分布函数（CDF）F（z）。

3 算法流程

综合以上分析，本文所提的考虑输入变量相关性的CM-LHS流程如图2所示，其主要由三部分组成：具有相关性的输入变量样本的产生、分段线性化潮流模型的处理以及改进后的半不变量法随机潮流计算。

4 算例分析

4.1 仿真参数与建模

为了说明本文所提CM-LHS算法的准确性和快速性，以IEEE 30节点系统为例进行仿真测试计算。如图3所示，算例中2个总装机容量均为10 MW的小型风电场分别接入节点29和30，它们的风速服从尺度参数为8.09、形状参数为2.17的双参数Weibull分布，且具有相关性，相关系数矩阵为：

风电场均采用恒功率因数控制方式，其输出特性可表示为：

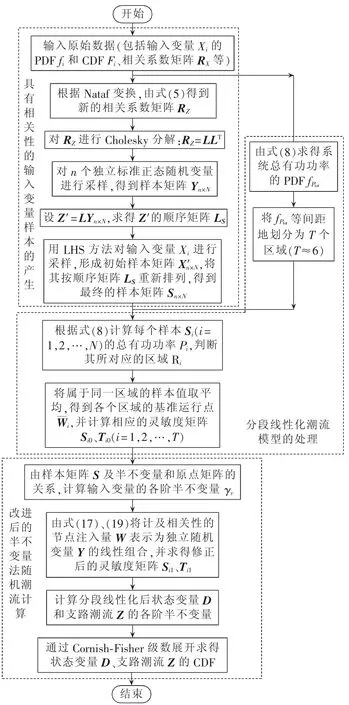
图2 考虑输入变量相关性的CM-LHS流程Fig.2 Flowchart of CM-LHS considering correlation between input variables

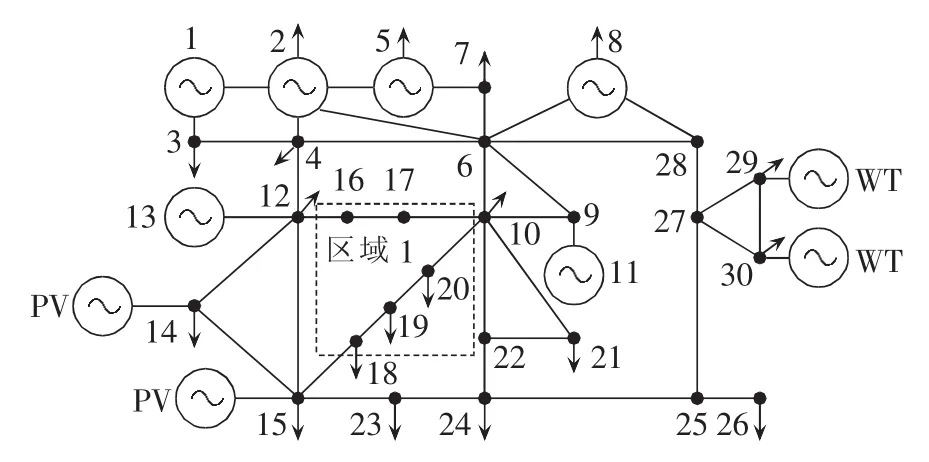
图3 IEEE 30节点测试系统Fig.3 IEEE 30-bus test system

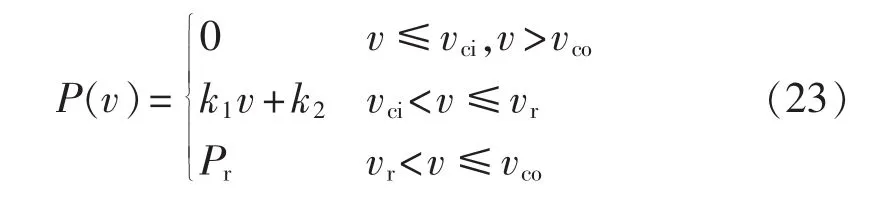
其中，k1=Pr/（vr-vci）；k2=-k1vci；Pr为风电场额定容量；vci、vr和vco分别为切入、额定和切出风速，分别为3 m /s、13 m /s和 20 m /s。

节点14和15还接有2个容量规格相同的太阳能光伏电站，其最大输出有功为1.5 MW，输出无功为0 Mvar，输出有功近似满足Beta分布：

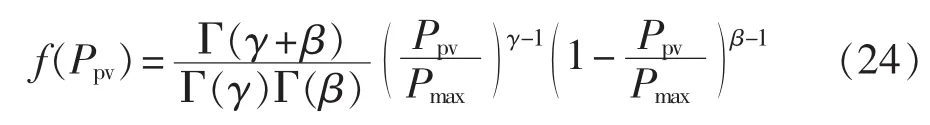
其中，Ppv和Pmax分别为光伏电站输出功率和最大功率；γ和β为形状参数，取γ=β=0.9。2个光伏电站的出力具有相关性，相关系数矩阵为：

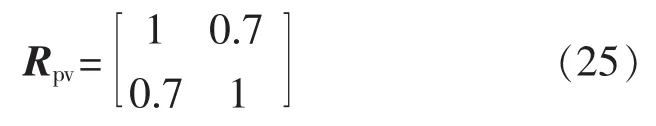
系统负荷服从正态分布，具体参数见文献［27］。其中区域1内的负荷具有相关性，包括节点16—20，其相关系数矩阵（按节点号从小到大）为：

根据算例参数模型及CM-LHS算法的流程，用MATLAB R2010b编制相应的程序，在配置Intel Core i3 CPU、主频2.53 GHz、内存2 GB的计算机上运行。

4.2 仿真结果与误差分析

以蒙特卡罗仿真（MCS）法所得结果作为参照，比较其他随机潮流算法的计算精度。取样本个数N=1000，分别求得各输出变量（节点10电压幅值、相角，支路 19-20 有功、无功）的期望和标准差［17］，作为基准值。为了综合全面地评估本文所提方法的准确性，引入相对误差与方差和的根均值ARMS（Average Root Mean Square）2项指标。其中相对误差主要反映本文方法所得结果与基准值的偏离程度：

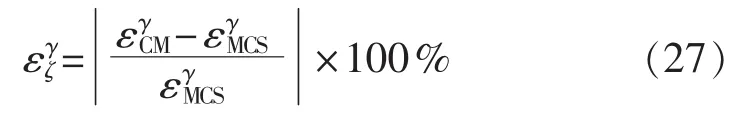
其中为相对误差指标；γ为输出变量类型（包括电压U、相角θ、有功P、无功Q）；ζ为随机变量的数字特征（包括期望 μ和标准差σ）。ARMS指标则用于衡量输出变量概率分布的计算精度，其定义为［28］：

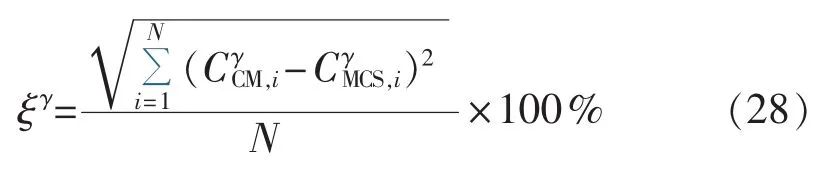
其中，ξγ为 ARMS 指标分别为本文CM-LHS方法和MCS法所得输出变量CDF上第i个点的值；N为CDF上的取点数，即样本个数。

表1给出了各输出变量相对误差的平均值和最大值为了分析本文所采用的分段线性化模型对计算精度的影响，将其与用单点线性化方程得到的误差结果进行比较。不同输出变量ARMS指标的平均值和最大值如表 2所示，其中样本点数N=1000。

表1 输出变量的相对误差指标Table 1 Relative errors of output variables %

表2 输出变量的ARMS指标Table 2 ARMS of output variables%

分析表1、表2可知，采用本文所提的分段线性化方法计算结果的精度明显高于传统的单点线性化方法，系统不确定程度越大，其优势越明显。且最大相对误差和最大 ARMS 指标均小于 2%，表明所提方法能够在考虑输入变量相关性的前提下准确反映输出变量概率分布的统计特性。

考虑风电、光伏的接入规模对所提算法的影响，对不同风电渗透率时系统误差进行测试，并与常规半不变量法比较，如图4所示。

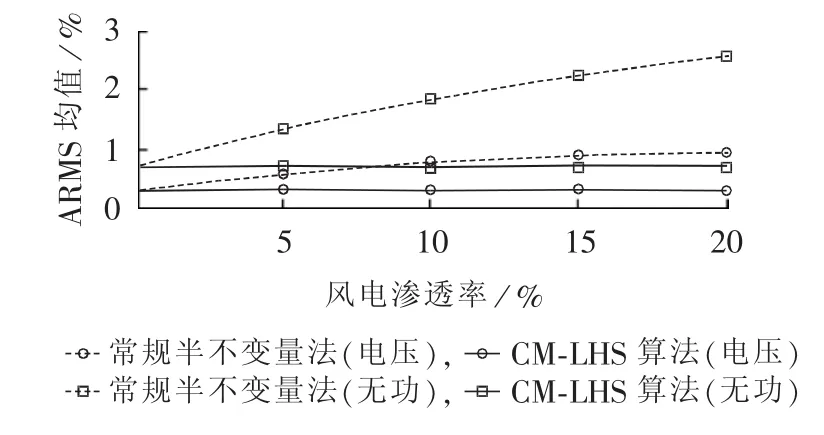
图4 不同风电渗透率的系统ARMS值Fig.4 Curve of ARMS vs.wind power penetration rate

由图4可见，随着风电比重的增加，常规半不变量法所得节点电压和支路功率的ARMS值逐步增大，而本文算法基本保持不变，能一直维持较高的精度。说明所提算法的稳定性好，可适用于大规模新能源并网的随机潮流分析。

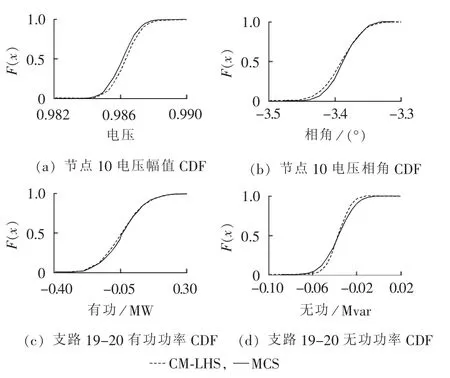
图5 不同输出变量的CDFFig.5 CDF of different output variables

图5给出了CM-LHS和MCS算法计算得到的不同输出变量的CDF（包括节点10电压幅值、相角，支路19-20有功和无功），图中电压幅值为标幺值。其中节点10和支路19-20都离新能源电站较近，受其出力波动的影响也较大，然而图5中通过本文方法得到的分布曲线依然能够保持较高的精度。

评估一个算法的有效性，除精度以外还必须考虑其计算耗时。表3比较了3种随机潮流算法在同精度级别下的计算时间，其中MCS方法的耗时远高于LHS方法和本文所提的CM-LHS，LHS方法虽然显著地提升了采样效率，但仍无法避免确定性潮流计算过程中的反复迭代。而CM-LHS综合了LHS方法的采样优势和半不变量法速度快的特点，耗时最少。以上仿真结果及分析验证了所提方法的准确性和快速性，进而可用来分析评估系统的静态安全性能。

表3 不同算法的计算时间Table 3 Calculating time of different algorithms

为了验证所提方法对大型网络系统的实用性，以IEEE 118节点系统为例进行分析，网络结构和线路参数详见文献［27］。假设系统负荷均服从高斯分布，标准差为均值的10%，不计负荷间的相关性。在节点2、39、52分别接入3座装机容量为150 MW、200 MW及350 MW的大型风电场，对应的相关系数为0.2、0.1和0.6，建模方式及参数同4.1节。

分别用MCS方法和CM-LHS进行测试，采样规模N=1000，得到所有输出变量的误差结果如表4所示。由表4可见，在网络规模和风电渗透率均较大的情况下，CM-LHS仍能准确地对系统运行特性进行评估（与相同采样规模的MCS方法相比）。以支路40-56的无功为例，如图6所示，CM-LHS和10000次采样的MCS方法得到的概率分布曲线大致相同，但耗时仅有7.42 s，约为后者的1/100，计算效率提升显著。

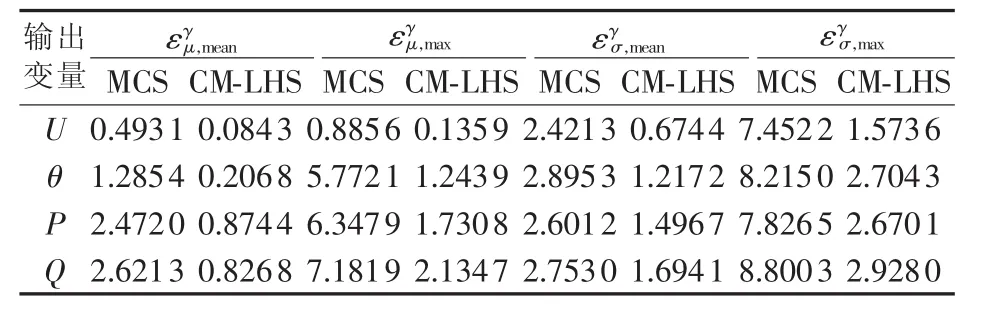
表4 IEEE 118节点系统2种方法输出变量的误差比较（N=1000）Table 4 Comparison of relative errors between two algorithms for output variables of IEEE 118-bus system（N=1000）%

图6 支路40-56注入无功概率分布Fig.6 Probabilistic distribution of reactive power injection to Line 40-56

5 结论

针对目前大多数随机潮流方法不能同时兼顾计算精度和耗时以及在处理相关性问题等方面的不足，本文提出一种考虑输入变量相关性的CM-LHS。该算法具有以下特点：（1）利用LHS技术提高采样效率，结合Nataf变换可方便地得到任意关联输入变量的样本；（2）采用分段线性化模型减小了潮流方程线性化引起的截断误差；（3）通过LHS所得样本计算出复杂输入变量的半不变量，解决其难以用常规数值方法求解的问题；（4）保留了半不变量法计算速度快的优势，并利用Cholesky分解克服其只能处理独立变量的局限。

算例测试结果验证了所提方法的准确性、快速性和实用性，能够较好地适应新环境下电网运行分析的要求。

［1］董朝阳，赵俊华，文福拴，等.从智能电网到能源互联网：基本概念与研究框架［J］.电力系统自动化，2014，38（15）：1-11.DONG Zhaoyang，ZHAO Junhua，WEN Fushuan，etal.From smartgrid to energy internet：basic concepts and research framework［J］.Automation of Electric Power Systems，2014，38（15）：1-11.

［2］赵海，蔡巍，王进法，等.能源互联网架构设计与拓扑模型［J］.电工技术学报，2015，30（11）：30-36.ZHAO Hai，CAI Wei，WANG Jinfa，et al.Energy internet architecture design and topology model［J］.Transactions of China Electrotechnical Society，2015，30（11）：30-36.

［3］ALLAN R N，AL-SHAKARCHI M R G.Probabilistic techniques in AC load-flow analysis［J］.Proceedings of the Institution of Electrical Engineers，1977，124（2）：154-160.

［4］XIE Kaigui，ROY B.Considering wind speed correlation of WECS in reliability evaluation using the time-shifting technique［J］.Electric Power System Research，2009，79（4）：687-693.

［5］范荣奇，陈金富，段献忠，等.风速相关性对概率潮流计算的影响分析［J］.电力系统自动化，2011，35（4）：18-22.FAN Rongqi，CHEN Jinfu，DUAN Xianzhong，et al.Impact of wind speed correlation on probabilistic load flow［J］.Automation of Electric Power Systems，2011，35（4）：18-22.

［6］丁明，李生虎，洪梅.电力系统概率分析中的K均值聚类负荷模型［J］.电力系统自动化，1999，23（19）：51-54.DING Ming，LIShenghu，HONG Mei.The K-means cluster based load model for power system probabilistic analysis ［J］.Automation of Electric Power Systems，1999，23（19）：51-54.

［7］彭寒梅，曹一家，黄小庆，等.基于组合抽样的含分布式电源随机潮流计算［J］.电力自动化设备，2014，34（5）：28-34.PENG Hanmei，CAO Yijia，HUANG Xiaoqing，et al.Probabilistic load flow calculation based on combination sampling for power system containing distributed generations［J］.Electric Power Automation Equipment，2014，34（5）：28-34.

［8］CARAMIA P，GARPINELLIG，VARILONE P.Pointestimate schemes for probabilistic three-phase load flow［J］.Electric Power System Research，2010，80（2）：168-175.

［9］ALLEN R N，LEITE DE S A M，BURCHETT R C.Evaluation methods and accuracy in probabilistic load flow solutions ［J］.IEEE Transactions on Power Apparatus and Systems，1981，100（5）：2539-2546.

［10］郭效军，蔡德福.不同级数展开的半不变量法概率潮流计算比较分析［J］.电力自动化设备，2013，33（12）：85-90.GUO Xiaojun，CAI Defu.Comparison of probabilistic load flow calculation based on cumulant method among different series expansions［J］.Electric Power Automation Equipment，2013，33（12）：85-90.

［11］程卫东.含风电场电力系统的概率潮流［D］.北京：华北电力大学，2010.CHEN Weidong.Probabilistic load flow for power grid containing wind farms［D］.Beijing：North China Electric Power University，2010.

［12］VILLANUEVA D，FEIJÓO A E，PAZOSJL.Ananalytical method to solve the probabilistic load flow considering load demand correlation using the DC load flow［J］.Electric Power Systems Research，2014，110（5）：1-8.

［13］KABIR M N，MISHRA Y，BANSAL R C.Probabilistic load flow for distribution systems with uncertain PV generation ［J］.Applied Energy，2016，163：343-351.

［14］MCKAY M D，BECKMAN R J，CONOVER W J.A comparison of three methods for selecting values of input variables in the analysis of output from a computer code ［J］.Technometrics，1979，21（2）：239-245.

［15］陈雁.含大规模风电场电力系统的运行与规划方法研究［D］.武汉：华中科技大学，2012.CHEN Yan.Study on the operation and planning of power system with large-scale wind farms［D］.Wuhan：Huazhong University of Science&Technology，2012.

［16］韩海腾，高山，吴晨，等.基于Nataf变换的电网不确定性多点估计法［J］.电力系统自动化，2015，39（7）：28-34.HAN Haiteng，GAO Shan，WU Chen，et al.Multi-point estimation method for power grid uncertainty based on Nataf transformation［J］.Automation of Electric Power Systems，2015，39（7）：28-34.

［17］石东源，蔡德福，陈金富，等.计及输入变量相关性的半不变量法概率潮流计算［J］.中国电机工程学报，2012，32（28）：104-113.SHI Dongyuan，CAI Defu，CHEN Jinfu，et al.Probabilistic load flow calculation based on cumulant method considering correlation between input variables［J］.Proceedings of the CSEE，2012，32（28）：104-113.

［18］EDWIN Haesen，CINDY Bastiaensen，JOHAN Driesen.A probabilistic formulation of load marginsin powersystemswith stochastic generation［J］.IEEE Transactions on Power Systems，2009，24（2）：951-958.

［19］吕大刚.基于线性化Nataf变换的一次可靠度方法［J］.工程力学，2007，24（5）：79-86.LÜ Dagang.First order reliability method based on linearized Nataf transformation［J］.Engineering Mechanics，2007，24（5）：79-86.

［20］MICGAEL S.Large sample properties of simulations using Latin hypercube sampling［J］.Technometrics，1987，29（2）：143-151.

［21］DA LEITE SILVA A M，ARIENTI V L.Probabilistic load flow by a multilinear simulation algorithm［J］.IEE Proceedings CGeneration，Transmission and Distribution，1990，137（4）：276-282.

［22］CARPINELLI G，DI V V，VARILONE P.Multi-linear Monte Carlo simulation forprobabilisticthree-phaseload flow ［J］.European Transactions on Electrical Power，2007，17（1）：1-19.

［23］GUIDO C，PIERLUIGI C.Multi-linear Monte Carlo simulation method for probabilistic load flow of distribution system with wind and photovoltaic generation systems［J］.Renewable Energy，2015，76：283-295.

［24］胡泽春，王锡凡，张显，等.考虑线路故障的随机潮流［J］.中国电机工程学报，2005，25（24）：26-33.HU Zechun，WANG Xifan，ZHANG Xian，etal.Probabilistic load flow method considering branch outages［J］.Proceedings of the CSEE，2005，25（24）：26-33.

［25］刘苏琴.考虑风电机模型的电力系统随机潮流计算［D］.南京：东南大学，2007.LIU Suqin.Probabilistic load flow in power system containing wind farms［D］.Nanjing：Southeast University，2007.

［26］朱星阳，刘文霞，张建华.考虑大规模风电并网的电力系统随机潮流［J］.中国电机工程学报，2013，33（7）：77-85.ZHU Xingyang，LIU Wenxia，ZHANG Jianhua.Probabilistic load flow method considering large-scale wind power integration［J］.Proceedings of the CSEE，2013，33（7）：77-85.

［27］CHRISTIE B R.Power system test casearchive ［EB/OL］.（2010-01-10）［2015-12-20］.http：∥www.ee.washington.edu /research/pstca.

［28］ZHANG P，LEE S T.Probabilistic load flow computation using the method of combined cumulants and Gram-Charlier expansion［J］.IEEE Transactions on Power Systems，2004，19（1）：676-682.