孤岛模式下光储直流微电网变功率控制策略

杨小龙，程启明，褚思远，张 强，黄 山

（上海电力学院 自动化工程学院，上海 200090）

0 引言

随着我国经济的发展，能源短缺与环境污染两大难题日益突出，发展清洁能源、保障能源安全是解决这两大难题最有效的途径［1-2］。然而太阳能、风能等清洁能源无法集中利用，为了更有效地利用这些清洁能源，微电网应运而生。微电网是将分布式电源、负荷和储能装置、变流器等有机整合在一起的小型发配电系统［3-5］，依据供给电能的类型，微电网可分为直流微电网、交流微电网和交直流混合微电网［6-10］。由于大电网与绝大多数负载都属于交流系统，所以交流微电网得到了较快的发展。然而直流微电网系统结构简单、能量转换少、供电质量高，相比交流微电网更有优势［11-13］，因此在如海岛、偏远的山区等地方因无法与大电网并网，直流微电网的运行更有效。本文选择以孤岛模式下的光储直流微电网为研究对象，并着重研究其控制策略。

目前直流微电网主要采用电压分层控制策略来控制其直流母线电压。文献［14］采用了分级控制，能够分层实现微电网的控制；文献［15］采用直流母线信号控制策略，通过采用直流母线信号实现微电网的最优控制；文献［16］采用自适应调节下垂系数，能够提高电池的运行效率。然而上述控制策略都没有考虑到因母线电压波动而导致控制策略频繁切换的情况。为解决母线电压波动对分层控制的影响，文献［17］在储能系统的充电模式和放电模式之间增加了空闲模式；文献［18］采取电压滞环控制。但是无论是增加空闲模式还是采取电压滞环控制都会造成控制延时而导致控制策略误切换的发生。

通过上述文献可知，直流微电网分层控制的主要思路为：电压是判定系统功率是否平衡的重要指标，通过检测电压是否恒定可以判定系统功率是否平衡，以直流母线电压的幅值为判定基准，将微电网的控制策略设置为不同工作模式［19］。然而分层控制以电压为判定基准就会不可避免地受到母线电压的影响，而直流微电网在正常运行时母线电压并非绝对的直流而是小范围内波动的，而且微电网不同模式切换时也会对母线电压造成一定的冲击，这些母线电压波动可能会导致微电网不同工作模式间的频繁切换，若通过增加蓄电池空闲模式或采取电压滞环控制等策略来解决这种状况，又会造成微电网控制的延时等一些新的问题。

为了解决电压分层控制问题，本文创新地提出了变功率控制方法。此方法以功率为判定基准，以铅酸电池的CIEMAT模型［20］为基础，利用微电网当前各个分布式单元输入输出功率，控制微电网工作于不同的控制策略。并根据光伏电池输出功率与负荷所消耗的功率差，控制蓄电池充放电功率的方向与大小，使微电网内功率能够保持平衡，进而使直流母线电压能够保持稳定。仿真结果验证了本文所提变功率控制方法的正确性，且其控制性能优于常用的电压分层控制方法。

1 常用的分层控制及其存在的问题

分层控制是当前直流微电网的控制策略中研究最广泛的控制策略。分层控制是将母线电压分为若干等级，然后根据母线电压的等级将微电网分为若干工作模式，通过各工作模式的切换使母线电压保持稳定。

孤岛模式下光储微电网某种分层控制策略见表1。表中，MPPT表示最大功率点跟踪。由表可知，分层控制将直流微电网的母线电压用4个阈值分为5个工作区域。在理想条件下，该分层控制能够很好地实现功率的平衡和电压的稳定。但实际上，直流微电网的母线电压并非严格的直流恒定值，电压会在小范围内波动且波动的频率较高，这将会导致微电网工作模式之间的误切换。产生电压波动的因素有微源、变流器、控制装置和负载等多种。

表1 光储微电网分层控制策略Table 1 Hierarchical control of photovoltaic-battery microgrid

下面以光伏的Boost变换器为例来说明变流器对电压的影响。

Boost变换器的拓扑结构如图1所示。

图1 Boost变换器拓扑结构Fig.1 Topological structure of Boost converter

在Boost变换器中，各电流与电压变化曲线如图2所示。由图可见，在Boost变换器中无论是电流ie还是输出电压uo，都是波动的而非绝对直流。

图2 Boost变换器的参数变化曲线Fig.2 Parameter variation curves of Boost converter

如果不考虑其他因素，Boost变换器中电容C与输出电压uo的关系如图3所示。图中，C1＞C2。

由图3可见，当电容C较大时，输出电压uo的波动较小，但此时Boost变换器稳定输出的延迟时间较长，而电网对各个变换器的瞬时性有较高的要求，即电容C不可能太大，因此输出电压uo的波动范围不可能很小或消失。

图3 Boost变换器中输出电压uo曲线Fig.3 Curves of output voltage uoof Boost converter

按表1所述的分层控制策略进行控制仿真，其直流母线电压的变化曲线如图4所示。

图4 分层控制时直流母线电压的变化曲线Fig.4 Variation curve of DC bus voltage in hierarchical control

由上面分析可知，直流微电网中的母线电压波动是无法消除的。分层控制以电压大小作为微电网工作模式切换的依据，母线电压在给定值附近上下高频波动，这将会使微电网在2种工作模式间高频切换，这种高频切换既会导致微电网内部大量能量的耗散，也会损害各个器件的寿命。由图4可见，母线电压会在52 V、54 V、56 V和58 V附近频繁波动，这些波动会使微电网的工作模式之间产生非正常的切换，相对于其他电压阈值，母线电压以52 V为中值上下波动时，将会导致某些负载频繁通断；而母线电压在54 V附近上下波动时，将会导致蓄电池反复进行充放电工作，这种情况可能会导致负载或蓄电池的损坏。 由图 4 中的子图（a）、（b）、（d）可见，这些非正常的工作模式之间的切换会对母线电压正常变化产生一定的冲击。

增加蓄电池空闲模式或采取电压滞环控制等策略可以解决这些问题，但是无论是蓄电池空闲模式还是电压滞环控制都会造成微电网正常工作模式间切换的延迟，这些延迟可能会造成图4中子图（e）所示的后果，即当微电网由模式1需要切换到模式2时，由于微电网动作的延迟，微电网由模式1经模式2直接切换到模式3，由于微电网需要在模式2正常运行而非模式3，所以微电网需要再由模式3切换到模式2，导致微电网在模式2与3之间波动切换，最终稳定在模式2。

此外，直流微电网内光伏电池输出的功率随外界条件的变化而变化，如24 h内光照强度从最弱到最强，然后再逐渐变成最弱，在理想条件下，光伏电池输出的电能也从最少到最多再逐渐减到最少，在这段时间内微电网的工作模式有可能从模式5逐渐切换到模式1，然后再逐渐切换到模式5。即在理想条件下24 h内微电网的工作模式需要切换8次，光伏电池的控制策略需要变换2次，蓄电池的控制策略需要变换6次。如果天气或者负载发生变化，这个时间间隔还要减少。微电网的工作模式或者说各个分布式单元的正常切换也会对微电网造成一定的冲击，如图4中子图（c）所示，而对分层控制而言，切换的次数太多也是其另一个不足之处。

2 本文提出的变功率控制方法

2.1 变功率控制系统的拓扑结构

针对上述电压的分层控制缺点，本文提出了直流微电网的变功率控制，为便于分析，本文采用孤岛式光储直流微电网，其拓扑结构图如图5所示，本系统由直流母线、光伏电池、储能装置、负荷、变流器和控制系统组成。

图5 变功率控制时孤岛式光储直流微电网结构框图Fig.5 Block diagram of islanded photovoltaic-battery DC microgrid in variable power control

图中，IPV为光伏电池输出电流；UPV为光伏电池输出电压；Ubus为直流母线电压；PPV为光伏电池输出功率；Pbattery为蓄电池输出功率；Pload为负荷功率；αM为MPPT控制模块输出的Boost电路的占空比；αB为恒压控制模块输出的Boost电路的占空比；α为光伏系统Boost电路实际占空比，当光伏系统采用MPPT控制时α=αM，当光伏系统采用恒压控制时α=αB。光伏电池输出低压直流电能，Boost变换器将光伏电池输出的电能转换为高压直流电能，并输出到直流母线上；蓄电池用于平抑光伏输出电能的波动，其充、放电状态与直流母线之间的功率流向为双向，通过双向DC/DC变换器与直流母线连接；微电网中负荷包括直流负荷与交流负荷2种，直流负荷通过DC/DC变换器与直流母线相连，交流负荷通过DC/AC变换器与直流母线相连；控制系统包括光伏电池的控制策略、蓄电池的控制策略和负荷的控制策略，本文重点研究了光伏电池和蓄电池的控制策略以及上述3种控制策略的配合。

2.2 变功率控制时微电网的4种工作模式

在图5所示的孤岛式光储直流微电网中，各分布式单元的控制策略主要包括光伏发电系统的控制策略、储能系统的控制策略、负载逐渐切除策略。直流微电网的工作模式是由上述3种控制策略之间相互配合构成，具体配合方式见表2。表中为光伏电池采用MPPT控制时输出的功率；分别为蓄电池的极限充电功率和极限放电功率。

表2 直流微电网的工作模式Table 2 Operating modes of DC microgrid

从表2可知，直流微电网的变功率控制是以功率为基准将微电网分为4种工作模式。

模式 1说明光伏电池最大发电功率除了负载消耗一部分，剩余的功率仍然超过蓄电池的极限功率。为了防止微电网内功率出现冗余，光伏电池采取恒压控制，使

模式 2说明光伏发电功率大于负载消耗功率，且剩余的功率在蓄电池的极限功率内。此时光伏采取MPPT控制，并需要根据ΔP′改变蓄电池的充电功率，使PPV-Pload=Pbattery_c。

模式 3说明光伏发电功率无法满足负载的消耗，需要蓄电池放电，且蓄电池需要放出的功率不超过其极限。为了维持功率的平衡需要根据ΔP′改变蓄电池放电功率，使Pload-PPV=Pbattery_d。

模式 4说明光伏电池发电功率严重不足，蓄电池需要放出的电能超过其极限放电功率。为了防止微电网内部出现严重功率缺额，需要根据负荷等级不同逐渐切除一部分负荷，使

2.3 3种分布式单元的控制策略

2.3.1 光伏电池的控制策略

光伏电池的控制原理如图5所示。由图可见，光伏电池分别工作于2种控制策略，即MPPT控制或恒压控制。

当光伏电池输出功率较少或蓄电池充电功率没有达到极限时，光伏电池采用MPPT控制输出其最大功率；而当光伏电池输出功率过多或蓄电池的充电功率达到极限时，需要减少光伏电池的输出功率，此时光伏电池采用恒压控制［19］。

2.3.2 蓄电池的控制策略

在直流微电网中蓄电池的控制是整个微电网协调控制的重心，因此本文重点研究了蓄电池充放电的控制方法。本文蓄电池采用CIEMAT模型［20］，见图6。图中，n为串联单体数量，Ubattery为蓄电池电压，Ibattery为蓄电池电流，Ebattery为电动势，R为蓄电池内阻。

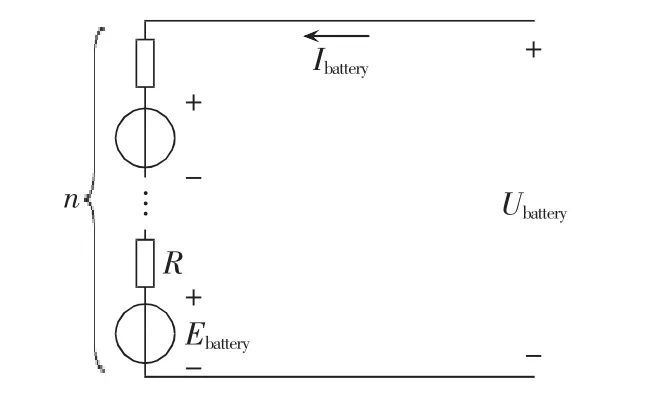
图6 蓄电池的CIEMAT模型结构Fig.6 Structure of battery CIEMAT model

在上述蓄电池的CIEMAT模型中，蓄电池充电功率为：

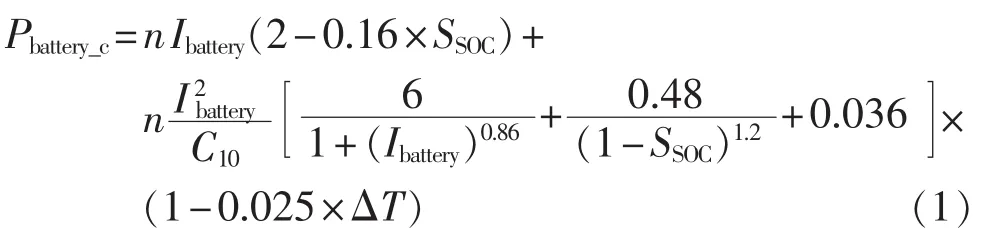
蓄电池放电功率为：

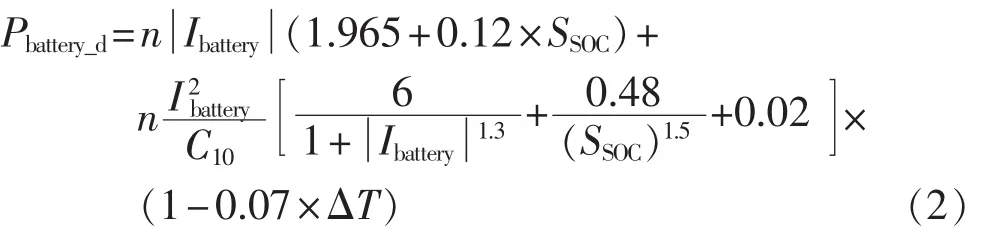
其中，ΔT=T-25℃，T为环境温度；SSOC为荷电状态（也称剩余电量），它为电池的剩余电量与其容量的比值，其取值为0～1；Ibattery为蓄电池电流，当蓄电池充电时 Ibattery＞0，当蓄电池放电时 Ibattery＜0；C10为蓄电池10 h率容量，单位为 A·h。

然而若要蓄电池安全高效地工作，就必须对蓄电池的充放电电流进行限制，设蓄电池的最大充电电流为最大放电电流为

如果直流微电网采用如表1所示的分层控制，当系统进入模式2或模式5时，如果蓄电池采用恒流充放电，由式（1）、（2）可知，当 SSOC、T 不变时蓄电池充放电功率恒定，即微电网在模式2或模式5内无论母线电压及系统功率如何变化，蓄电池的充放电功率都保持恒定，即蓄电池充电功率不能随着母线电压的升高及系统内剩余功率的增多而增多，这就导致蓄电池对微电网功率的调节功能显得比较生硬不够灵活。

本文的蓄电池采取变功率控制，其中蓄电池的充放电功率是由光伏发电功率与负荷功率所决定，并由母线电压的额定变化值作为补充，并且根据蓄电池充放电功率的大小决定蓄电池的工作状态。即：如果则说明蓄电池的充放电功率没有达到极限，此时蓄电池工作于非极限充（放）电状态；如果则说明蓄电池的充放电功率达到了极限，此时蓄电池工作于极限充（放）电状态，而且通过调节蓄电池与微电网系统的各个参数使

根据上述分析，本文所采取的蓄电池控制原理如图7所示。由图可见，蓄电池主要采用非极限变功率控制和极限变功率控制2种控制模式。

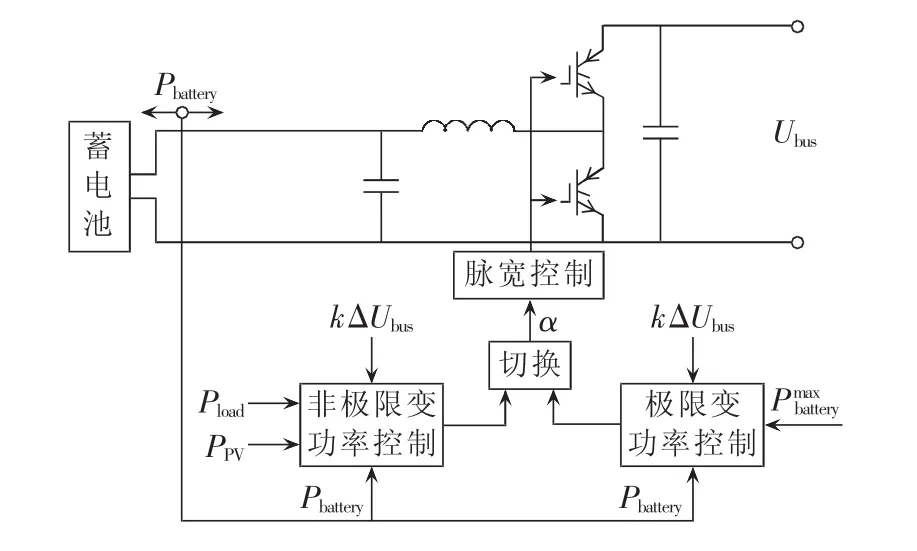
图7 蓄电池控制原理框图Fig.7 Schematic diagram of battery control

（1）非极限变功率控制。

非极限变功率控制的控制算法框图如图8所示。图中，αc为蓄电池充电时双向DC/DC电路中Buck电路的占空比；αd为蓄电池放电时双向DC/DC电路中Boost电路的占空比。非极限变功率控制的原理为：通过公式计算蓄电池充放电功率的给定值，然后使蓄电池工作在给定值附近以调节微电网功率的平衡。

图8 非极限变功率控制算法框图Fig.8 Block diagram of non-limit variable power control algorithm

当PPV＞Pload时，蓄电池工作于充电状态且Pref_battery_c=PPV－Pload。此时如果母线电压升高，则说明微电网内功率因计算、测量有误差而导致微电网内还有冗余功率，此时应该增加蓄电池充电功率，即为：

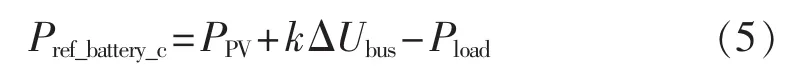
其中，ΔUbus为母线额定电压变化量；k为母线电压转换为冗余功率的系数。

当PPV＜Pload时，蓄电池工作于放电状态且Pref_battery_d=Pload－PPV。此时如果母线电压升高说明微电网内有冗余功率，此时应该减少蓄电池放电功率，即为：

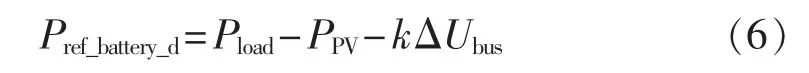
（2）极限变功率控制。

从式（5）、（6）可知，蓄电池的充放电极限功率随着SSOC、T的变化而变化，蓄电池极限功率控制主要是通过SSOC、T和蓄电池最大允许充放电电流计算其极限功率，再加上因误差而导致的电压变化的修正，控制蓄电池充放电功率，使蓄电池始终安全稳定地工作于极限功率下。其控制算法框图如图9所示。

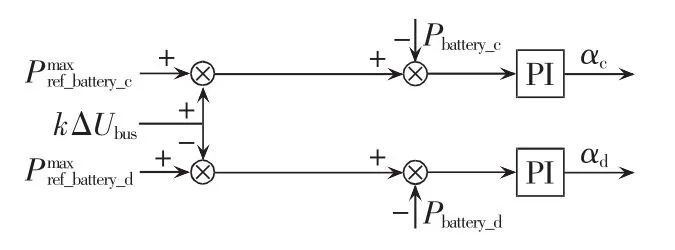
图9 极限变功率控制算法框图Fig.9 Block diagram of limit variable power control algorithm

2.3.3 负荷的控制策略

由于蓄电池的放电功率具有极限值，如果光储微电网中光伏输出功率与蓄电池极限放电功率之和依旧小于微电网系统的负荷功率，即此时微电网的发电功率无法满足负荷的消耗，所以此时微电网中的功率将无法达到平衡，这将导致整个微电网系统处于不稳定状态。

因此当微电网总的极限输出功率小于负荷功率时，需要采取如图5所示的控制策略，通过断路器逐渐切除负荷使得进而保证微电网功率的平衡。

3 仿真验证

为了验证上述控制策略的有效性和可行性，本文在MATLAB/Simulink中搭建了直流微电网变功率控制的模型并进行了一系列仿真。

3.1 直流微电网的稳定性仿真

图10为当光伏电池的输出功率具有较大波动时直流微电网的母线电压和冗余功率（Pex=PPV-Pload-Pbattery）的变化曲线。图中，当t=5 s时光伏电池的输出功率由70 W突变为175 W。

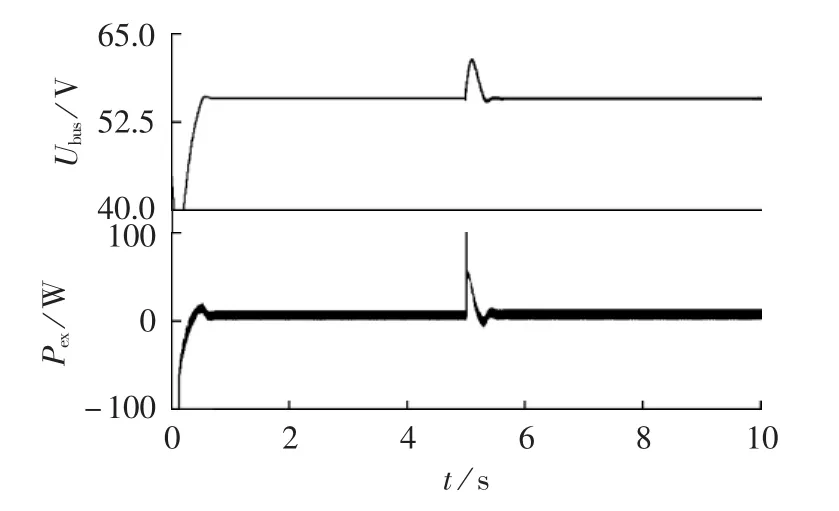
图10 光伏输出功率突变时微电网各参数变化曲线Fig.10 Parameter variation curves of Boost converter during photovoltaic power output mutation

图11为当负荷有较大波动时，直流微电网的母线电压和冗余功率的变化曲线。图中，当t=5 s时直流微电网的负荷功率由120 W突变为200 W。

图11 负荷突变时微电网各参数变化曲线Fig.11 Parameter variation curves of Boost converter during load power mutation

由图10、图11可以看出，无论是光伏电池输出功率的突变还是直流微电网负荷的突变，在突变后，直流微电网的母线电压都稳定在额定值附近，这说明直流微电网系统的母线电压能保持稳定；而且在突变后直流微电网的冗余功率都约等于零，这说明直流微电网系统的功率能保持平衡。

由此可知，光伏功率和负荷突变时微电网能够保持稳定。

3.2 冗余功率系数k对微电网影响仿真

图 7—9 及式（5）、（6）中的微电网冗余功率系数k的正确取值对微电网母线电压偏离额定值的大小以及微电网稳定性都有重要的影响。

图12为冗余功率系数k不同时直流母线电压的变化曲线（图中 k′=Pload/（0.01Ubus））。图中，在 t=5 s时光伏电池输出功率突然增大，蓄电池由变功率放电模式变为变功率充电模式。

由图12可见，在微电网工作模式发生变化时，只有当k≈k′时，微电网直流母线电压才稳定在额定值附近，此时微电网母线电压的偏离较小，微电网具有较好的稳定性；而无论当k≪k′时还是当k≫k′时，微电网母线电压都有一段偏离其额定值比较大的区域，且当k≫k′时（即k过大时）微电网系统的稳定性较差。因此，只有当k≈k′时，微电网工作的稳定性及微电网运行效果才比较好。

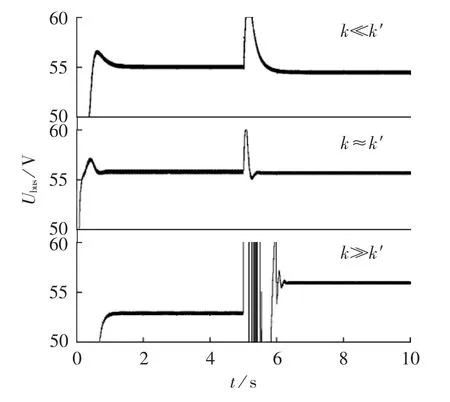
图12 冗余功率系数k不同时直流母线电压的变化曲线Fig.12 Variation curve of DC bus voltage for different values of redundant power coefficient k

3.3 1 d内直流微电网各参数的变化趋势仿真

为了更鲜明且更简便地说明变功率控制的优点，本文根据1 d内太阳的变化在20 s内模拟了1 d内光照强度S的变化趋势，其变化曲线如图13所示。在仅光照强度变化时光伏电池输出功率的变化情况如图14所示。

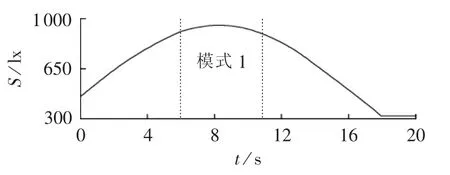
图13 光照强度变化曲线Fig.13 Variation curve of light intensity

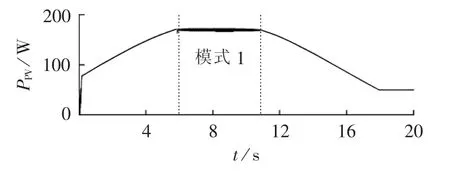
图14 光伏电池的输出功率变化曲线Fig.14 Variation curve of photovoltaic cell output power

图14中，当t=6～10.9 s时，系统处于模式1状态，此时光伏电池工作于恒压控制模式下，而其他时间则工作于MPPT模式下。

当微电网负荷都是较大功率负荷时，如果微电网工作在模式4，此时需要切除负荷，由于负荷都较大，切除一部分负荷时微电网负荷功率会突然减小，这就使得微电网蓄电池放电功率减小，微电网退出工作模式4，而重新进入工作模式3。微电网内部光伏负荷功率差（ΔP′=PPV-Pload）、蓄电池输出功率及负荷功率变化曲线如图15所示。

由图15可得如下结论：

图15 负荷较大时微电网各功率参数变化曲线Fig.15 Power parameter variation curves of microgrid with heavy load

（1）当 t=0～2.4 s时，ΔP′＜0，光伏电池输出功率不能满足负荷的消耗，此时Pbattery＞0，蓄电池工作在非极限变功率放电模式，系统工作在模式3；

（2）当 t=2.4～6 s时，ΔP′＞0，光伏电池输出功率大于负荷的消耗功率，此时Ibattery＜0，蓄电池工作在非极限变功率充电模式，系统工作在模式2；

（3）当t=6～10.9 s时，由于蓄电池充电功率达到极限，此时蓄电池工作在极限变功率充电模式，光伏电池工作于变压控制模式，且由于此时微电网负荷不变，此时光伏输出功率不变，系统工作在模式1；

（4）当t=10.9～14 s时，由于光伏输出功率的减小，蓄电池的充电功率减小，使得蓄电池退出极限变功率充电模式，此时蓄电池工作在非极限变功率充电模式，系统工作在模式2；

（5）当 t=14～16.8 s时，ΔP′＜0，光伏电池输出功率不能满足负荷的消耗，此时Pbattery＞0，蓄电池工作在非极限变功率放电模式，系统工作在模式3；

（6）当t=16.8～17 s时，蓄电池充电功率达到极限，蓄电池工作在极限变功率放电模式，此时微电网切除一部分负荷，使负荷功率Pload减小，由于负荷功率的减小，蓄电池放电功率减小，使得蓄电池退出极限变功率放电模式，工作在非极限变功率放电模式，系统工作在模式4；

（7）当t=17～18 s时，随着光伏输出功率的减小，蓄电池放电功率逐渐增加，系统工作在模式3；

（8）当t=18～20 s时，蓄电池放电功率达到极限，由于光强的恒定光伏输出功率不变，此时不需要切除负荷，所以负荷不变，系统工作在模式4。

当微电网具有较小负荷时，如果微电网蓄电池放电功率达到极限，微电网工作于模式4，此时需要切除负荷时，可以逐渐切除小功率负荷，使蓄电池放电功率始终维持在极限值附近，这样就使得微电网始终工作于模式4。微电网蓄电池充放电功率曲线和负荷曲线如图16所示。

图16 负荷较小时微电网各功率参数变化曲线Fig.16 Power parameter variation curves of microgrid with light load

3.4 变功率控制的优势

以大功率负荷为例，当光照强度按照如图13所示的曲线变化时，图17为直流微电网在采用2种不同控制控制策略时蓄电池输出功率变化曲线。图中，Pbattery＜0表示充电；Pbattery＞0表示放电。由图可见，微电网在采用变功率控制时蓄电池的输出功率曲线明显优于采用分层控制时蓄电池的输出功率曲线。其主要原因在于：在同样条件下，分层控制时蓄电池工作模式切换的次数明显多于变功率控制时蓄电池工作模式的切换次数，而蓄电池工作模式每切换一次都会对蓄电池正常工作产生一定影响。

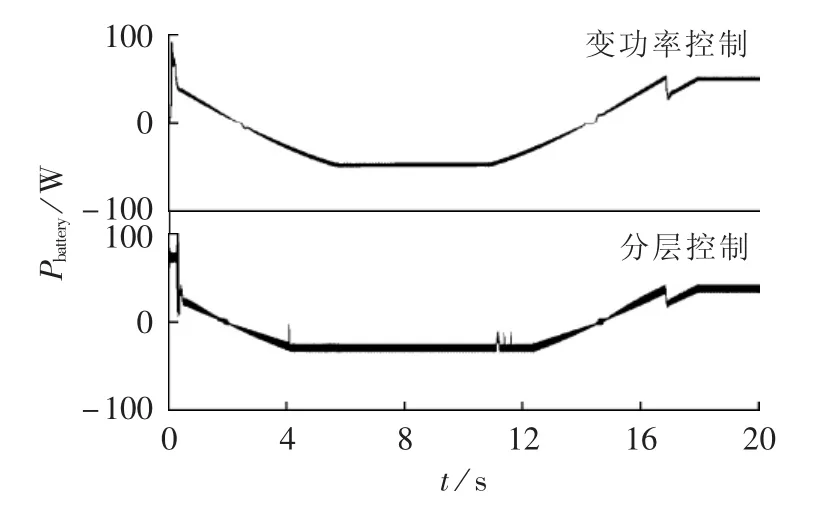
图17 2种不同控制策略下蓄电池输出功率变化曲线Fig.17 Variation curve of battery output power by two control strategies

图18为直流微电网在采用2种不同控制策略时母线电压变化曲线，其中母线电压的变化代表了直流微电网母线电压的稳定性。

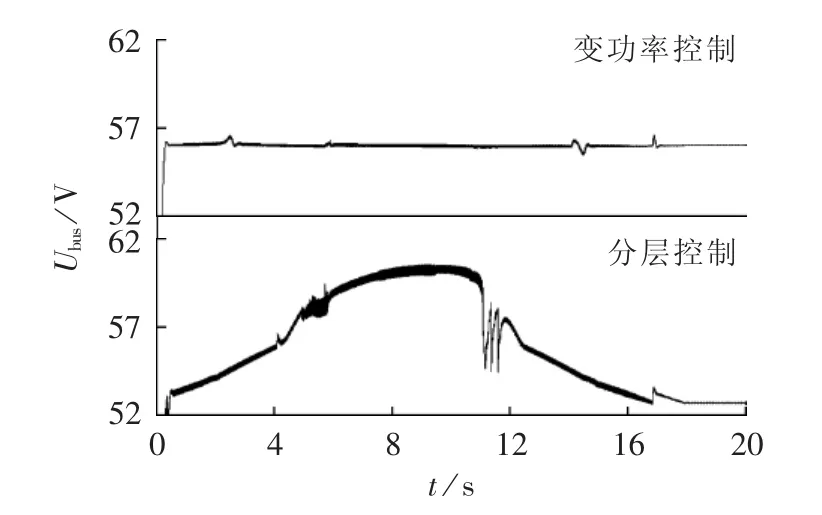
图18 2种不同控制策略下直流微电网母线电压变化曲线Fig.18 Variation curve of DC bus voltage of DC microgrid by two control strategies

图19为直流微电网在采用2种不同控制策略时冗余功率变化曲线，其中冗余功率的大小代表了直流微电网功率的平衡性。

图19 2种不同控制策略下直流微电网冗余功率变化曲线Fig.19 Variation curve of redundant powers of DC microgrid by two control strategies

由图17—19可知，当直流微电网分别采取变功率控制和分层控制时，蓄电池的切换次数N、母线电压波动的大小冗余功率波动的大小如表3所示。

表3 变功率控制和分层控制时微电网各参数值Table 3 Parameters of microgrid in variable power control and hierarchical control

由表3可知，无论是蓄电池充放电的次数、母线电压波动的大小还是微电网冗余功率波动的大小，变功率控制都明显小于分层控制，即蓄电池使用寿命、微电网母线电压的稳定性、微电网功率的平衡性，变功率控制都明显优越于分层控制。

4 结论

本文通过分析直流微电网中以电压为基准将控制策略分为不同模式的分层控制策略的不足之处，创新地提出了以功率为基准将控制策略分为不同模式的变功率控制策略以实现微电网内功率的平衡和电压的稳定。最后通过仿真验证了本文所提的变功率控制方法明显优于常用的分层控制方法，并可得出以下结论：

（1）蓄电池采用变功率充放电控制，能够实现微电网内部功率的平衡；

（2）将直流微电网母线电压差加入到蓄电池充放电的给定值计算公式中，能够消除因计算误差或测量误差导致微电网内功率的不平衡；

（3）实现微电网内功率的平衡就能实现直流微电网母线电压的稳定。

［1］郑永伟，陈民铀，李闯，等.自适应调节下垂系数的微电网控制策略［J］.电力系统自动化，2013，37（7）：6-11.ZHENG Yongwei，CHEN Minyou，LI Chuang，et al.A microgrid control strategy based on adaptive drooping coefficient adjustment［J］.Automation of Electric Power Systems，2013，33（7）：6-11.

［2］武星，殷晓刚，宋昕，等.中国微电网技术研究及其应用现状［J］.高压电器，2013，49（9）：142-149.WU Xing，YIN Xiaogang，SONG Xin，et al.Research on microgrid and its application in China［J］.High Voltage Apparatus，2013，49（9）：142-149.

［3］李斌，宝海龙，郭力.光储微电网孤岛系统的储能控制策略［J］.电力自动化设备，2014，34（3）：8-15.LI Bin，BAO Hailong，GUO Li.Strategy of energy storage control for islanded microgrid with photovoltaic and energy storage systems［J］.Electric Power Automation Equipment，2014，34（3）：8-15.

［4］HATZIARGYRIOU N，ASAND H，IRAVANI R，et al.Microgrids［J］.IEEE Power and Energy Magazine，2007，5（4）：78-94.

［5］薛贵挺，张焰，祝达康.孤立直流微电网运行控制策略［J］.电力自动化设备，2013，33（3）：112-117.XUE Guiting，ZHANG Yan，ZHU Dakang.Operationalcontrol strategy of stand-alone DC microgrid［J］.Electric Power Automation Equipment，2013，33（3）：112-117.

［6］BRACALE A，CARAMIA P，CARPINELLI G，et al.Optimal control strategy of a DC micro grid［J］.International Journal of Electrical Power&Energy Systems，2015，67（3）：25-38.

［7］LIU Xiong，WANG Peng，LOH P C.A hybrid AC/DC microgrid and its coordination control［J］.IEEE Transactions on Smart Grid，2011，2（2）：278-286.

［8］白园飞，程启明，吴凯，等.独立交流微电网中储能电池与微型燃气轮机的协调控制［J］.电力自动化设备，2014，34（3）：65-70.BAI Yuanfei，CHENG Qiming，WU Kai，et al.Coordinated control of storage battery and microturbinin islanded AC microgrid［J］.Electric Power Automation Equipment，2014，34（3）：65-70.

［9］周稳，戴瑜兴，毕大强，等.交直流混合微电网协同控制策略［J］.电力自动化设备，2015，35（10）：51-57.ZHOU Wen，DAI Yuxing，BI Daqiang，et al.Coordinative control strategy for hybrid AC-DC microgrid［J］.Electric Power Automation Equipment，2015，35（10）：51-57.

［10］李玉梅，查晓明，刘飞，等.带恒功率负荷的直流微电网母线电压稳定控制策略［J］.电力自动化设备，2014，34（8）：57-64.LI Yumei，ZHA Xiaoming，LIU Fei，et al.Stability control strategy for DC microgrid with constant power load［J］.Electric Power Automation Equipment，2014，34（8）：57-64.

［11］施婕，郑漳华，艾芊.直流微电网建模与稳定性分析［J］.电力自动化设备，2010，30（2）：86-90.SHI Jie，ZHENG Zhanghua，AI Qian.Modeling of DC micro-grid and stability analysis［J］.Electric Power Automation Equipment，2010，30（2）：86-90.

［12］吴卫民，何远彬，耿攀，等.直流微网研究中的关键技术［J］.电工技术学报，2012，27（1）：98-106.WU Weimin，HE Yuanbin，GENG Pan，et al.Key technologies for DC microgrids［J］.Transactions of China Electrotechnical Society，2012，27（1）：98-106.

［13］王毅，张丽荣，李和明，等.风电直流微网的电压分层协调控制［J］.中国电机工程学报，2013，33（4）：16-24.WANG Yi，ZHANG Lirong，LI Heming，et al.Hierarchical coordinated control of wind turbine-based DC microgrid ［J］.Proceedings of the CSEE，2013，33（4）：16-24.

［14］GUERRERO J M，VASQUEZ J C，MATAS J，et al.Hierarchical control of droop-controlled AC and DC microgrids-ageneral approach toward standardization［J］.IEEE Transactions on Industrial Electronics，2011，58（1）：158-172.

［15］支娜，张辉，邢小文.直流微电网协调控制策略研究［J］.西安理工大学学报，2012，28（4）：421-426.ZHI Na，ZHANG Hui，XING Xiaowen.DC microgrid coordinated control strategy research［J］.Journal of Xi’an University of Technology，2012，28（4）：421-426.

［16］刘家赢，韩肖清，王磊，等.直流微电网运行控制策略［J］.电网技术，2014，38（9）：2356-2362.LIU Jiaying，HAN Xiaoqing，WANG Lei，et al.Operation and control strategy of DC microgrid［J］.Power System Technology，2014，38（9）：2356-2362.

［17］秦文萍，柳雪松，韩肖清，等.直流微电网储能系统自动充放电改进控制策略［J］.电网技术，2014，38（7）：1827-1834.QIN Wenping，LIU Xuesong，HAN Xiaoqing，et al.An improved controlstrategy ofautomaticcharging/dischargingofenergy storage system in DC microgrid［J］.Power System Technology，2014，38（7）：1827-1834.

［18］范柱烽，毕大强，任先文，等.光储微电网的低电压穿越控制策略研究［J］.电力系统保护与控制，2015，43（2）：6-12.FAN Zhufeng，BI Daqiang，REN Xianwen，et al.Low voltage ride-through control of the photovoltaic/battery micro-grid system［J］.Power System Protection and Control，2015，43（2）：6-12.

［19］毕大强，范柱烽，解东光，等.海岛光储直流微电网自治控制策略［J］.电网技术，2015，39（4）：886-891.BI Daqiang，FAN Zhufeng，XIE Dongguang，et al.Autonomous control strategy of island DC microgrid with photovoltaic and storage system［J］.Power System Technology，2015，39（4）：886-891.

［20］ACHAIBOU N，HADDADI M，MALEK A.Lead acid batteries simulation including experimental validation［J］.Journal of Power Sources，2008，185（2）：1484-1491.