管拱型钢波纹管涵洞有限元计算分析

李祝龙，曹 彪，梁养辉，姜 涛，郭力源

(1. 重庆交通大学 土木工程学院， 重庆400074；2. 中交第一公路勘察设计研究院有限公司 西安中交环境工程有限公司， 陕西 西安 710075)

管拱型钢波纹管涵洞有限元计算分析

李祝龙1,2，曹 彪1，梁养辉2，姜 涛1，郭力源2

(1. 重庆交通大学 土木工程学院， 重庆400074；2. 中交第一公路勘察设计研究院有限公司 西安中交环境工程有限公司， 陕西 西安 710075)

为拓展钢波纹管的应用型式，运用大型有限元分析软件建立合理的力学有限元模型，对管拱型钢波纹管涵洞的受力变形进行了计算分析。运用有限元法分析得出管拱型钢波纹管涵洞土体受力变形规律。在建立的有限元模型中，通过施加公路-Ⅰ级荷载分析得出，填土高度对不同的拱顶角度的管拱型钢波纹管的周向等效应力、最大等效应力、横向位移、竖向位移的变化规律，确定了最优管型。对管拱型钢波纹管涵洞在公路工程中的发展、运用具有重要现实指导意义。

道路工程；管拱型钢波纹管涵洞；有限元；拱顶角度；填土高度

0 引 言

将钢板卷曲成波纹一直被熟知，这能够增强其刚度和强度。第一轧钢厂建于英国1784年，波纹钢板已经被生产出来。钢波纹管运输方便，该结构涵洞施工简单、工期短、在修筑过程中对地基扰动小、对基础要求较低、适应地基变形性能好等诸多优点。轴向波纹存在能更好地分散荷载的集中应力，使其具有良好的抗拉、抗剪和抗疲劳能力，更好的发挥钢结构的优势。尤其适用于边远地区或多年冻土、软土、膨胀土和湿陷性黄土等特殊地基区域的道路涵洞工程。因此，钢波纹管涵洞在我国具有广阔的应用前景[1-3]。

钢波纹管涵洞在我国交通工程中的应用已经比较广泛，截面型式几乎全部都是圆形，至今鲜有其它截面型式出现。放眼国外钢波纹管涵洞的应用则有着较多截面型式。其中，管拱型结构是比较具有优势的一种管型结构。该结构净空较小，具有水力优势，可做涵洞、下水道、立交桥、雨水管等[4-5]。为丰富我国钢波纹管的截面型式，需要对不同的截面型式的钢波纹管涵进行有限元模拟计算分析。笔者通过对管拱型钢波纹管的有限元计算分析得出了该截面型式的钢波纹管应力分布规律和横向、竖向位移规律；研究了管周土体的应力分布现象；得出最优管拱截面型式。为该结构在工程实际中的应用给出了一定的指导性意见。

1 管拱钢波纹管的截面型式

管拱钢波纹管横截面型式由3组不同半径的圆弧波纹钢板组成，其中包括半径Rt的顶部圆弧波纹钢板；半径Rc的腰部圆弧波纹钢板，左右各一块；半径Rb的底部圆弧波纹钢板[4]。同样的3组圆弧波纹钢板不同的拱顶角度(θ)可以设计出不同的截面型式，见图1。

图1 管拱截面示意Fig.1 Sectional schematic of pipe-arch corrugated steel pipe

2 有限元模型的建立

为达到和满足计算结果接近实际的要求，运用有限元软件建立与现场实际情况相接近的模型。同时把一些不可能模拟的情况进行了一定的简化。假定钢波纹管和土体共用相同的节点，不考虑土体与涵洞的接触问题[2]。在圣维南原理的基础上选取5个波长的局部管体进行建模，土体和砂砾按照弹性体进行计算[6-7]。

将波纹管的单元类型取为壳体单元，将土体单元取为六面体8节点实体单元。划分有限元单元网格的顺序为：先划分波纹钢管，钢管的单元划分为四边形，并应使每个单元的长宽比接近于1[8]，见图2。后划分波纹管周边的土体，土体划分成接近于正六面体的单元。在该结构中使用壳体单元可以非常接近地模拟涵洞受力[2，8]。整体涵洞模型见图3。

图2 局部管体网格划分Fig.2 Meshing of partial tube

图3 整体涵洞模型Fig.3 Model of culvert

2.1 材料属性与参数选择

有限元模型取Rt=4.043 m，Rc=1.390 m，Rb= 9.190 m，拱顶角度θ分别取135°,150°,165°,180°[9]。钢波纹管波形选用152×51，波峰、波谷曲率半径R=29 mm，壁厚t=6 mm，钢管壁取shell63四节点壳体单元。所选材料参数见于表1。

表1 材料参数Table 1 Material parameters

2.2 计算理论依据

3 应力分布云图

按照(DB15/T654—2013)《公路波纹钢管(板)桥涵设计与施工规范》进行填土。图4为钢波纹管涵洞顶部填土高度为0.6,1.0m的涵洞钢管应力分布云图。从图4可以看出，填土高度0.6m时钢波纹管波峰、波谷最大应力都出现在顶部。填土高度为1m的管拱钢波纹管的最大应力出现在管拱左、右两侧腰部圆弧部分的波谷(从外侧看)处。最小应力出现在底部圆弧的波谷处。波峰处最大应力出现在拱顶圆弧的正上方。说明低填方在公路-Ⅰ级荷载[12]的作用下钢波纹管的顶部应力增加，且填方越低管顶应力增加越明显。

图4 钢波纹管应力云图Fig.4 Stress cloud of arch corrugated steel culvert

图5填土高度为1，3，5，15，25 m时土体等效应力云图。从图5可以看出，填土高度为3，5，15，25 m管拱钢波纹管涵洞的土体最大应力同样出现在管子左、右两侧腰部圆弧部位处。同时，涵管最大应力也出现在该部位，工程运输中也是比较容易撞击到涵管该部位，所以应加强运输安全保护。工程施工拼装填土过程中应加强该部位应力监测。

图5 不同填土高度土体等效应力云图Fig.5 Equivalent stress cloud of different soil filling height

埋式管道垂直土压力本质是管道本身与两侧土体刚度的不同引起了管顶垂直土压的变化[13]。从图5反映了填土高度变化对土体等效应力影响，可以看出，公路-Ⅰ级荷载对下部土体的影响较小。管子底部两侧较中间部位的土压力大。根据截面型式为圆形的钢波纹管施工过程，管子两侧楔子部分既土体压力最大处是土体最难压实部位。从图5看出，管子上方的土压力表现出大写字母“M”形状的变化规律，即在相同的一层土体内等效应力从左向右为先增大后减小再增大最后减小。管周土体最大等效应力分布在腰部圆弧钢板的下部，填土高度越低管周的等效应力值越小，随着填土高度的增加腰部圆弧下部的等效应力也随之增大，因此在施工过程中要注意这楔形部分的土体密实度。可用水密法进行密实，也可以换填级配碎石。

4 有限元计算结果及分析

钢波纹管模型关于1 #点，12 #点轴线对称(如图6)。

图6 管周节点编号Fig.6 The number around the tube

取模型的一半作为研究对象。在有限元中按照单元节点划分管周的编号，即把单元划分得足够精细。在选取节点编号时使得1 #～6 #各点之间夹角为15°，6 #～10 #各点之间夹角为10°，10 #～11 #点夹角为15°，11 #～12 #点夹角为50°。抽取波峰和波谷对应的点，从上到下依次为1 #～12 #，抽取管周所标注点的等效应力值，分析所标注点的应力大小。应力变化在腰部圆弧处变化较复杂，因此该部位较稠密，顶部、底部较稀松。

4.1 钢波纹管周的等效应力

通过对135°，150°，165°，180°拱顶角度的管拱型波纹管进行了有限元计算分析。得出管周等效应力、最大的等效应力、竖向变形、横向变形分别随着填土高度和拱顶角度变化规律，见图7。

图7 不同拱顶角度下波谷管周等效应力Fig.7 Equivalent stress diagram at trough of different vault radian

从图7各图可以看出相同的规律，随着测点编号的变化，填土高度为0.6，1.0 m的管周波谷应力表现为先减小后增大再减小的趋势。3，5，15，25 m填土高度管周波谷应力变化曲线的趋势是先增大后减小再增大最后减小。说明随着填土高度增加荷载对波纹管顶部的应力作用减弱。从图7看出，在4 #～6 #点，高填方的波谷应力值出现一段减小的趋势，这和图5的观察是相对应的，说明由于该部分土体向下的压力作用在钢波纹管上造成的。从图7(a)～图7(c)中看出最高点出现在7 #点附近。在图7(d)的最高点出现在8 #点附近。说明随着填土增加波谷“应力重心”向下部移动。同时看出，管底的应力值很小不影响结构的安全与稳定性。

图8 不同拱顶角度下波峰管周等效应力Fig.8 Equivalent stress diagram at crest of different vault radian

从图8各图中可以看出波峰处的应力值表现出相同的比较活跃的波动性。在低填方下管周波峰等效应力波动幅度较高填方小，呈现出在2×107Pa上下波动。在高填方的作用下从1#点到12#点应力曲线表现出“骆驼峰”的形状趋势，随着填土高度的增加峰值越大，并且，前峰值大于后峰值，前峰值随着填土高度的增加从5 #位向6 #位移动。结合图7可以得知，这两个峰值出现在波谷等效应力峰值的两侧位置。说明波峰和波谷的存在使钢波纹管具有较大的惯性矩，在受力时波峰和波谷可以同时承受外部荷载。

4.2 钢波纹管的最大等效应力

从图9中可以看出，随着填土高度的增加不同拱顶角度管拱最大等效应力表现为先减小后变大，在填土高度为1m时达到最小值。表明在填土高度低于1 m时荷载对最大等效应力起到控制作用，填土高度大于1 m时填土高度对最大应力起到控制作用。相对于填土荷载，车辆荷载对涵管的最大等效应力的影响减弱。

图9 最大等效应力与填土高度曲线Fig.9 The maximum equivalent stress of filling height

从图10看出，在相同填土高度的情况下，填土高度0.6 m时最大等效应力随拱顶角度增大而减小，这时最大等效应力出现在拱顶部，较填土1 m时最大等效应力大。填土高度1 m时最大等效应力随着填土高度增加先减小后增大，在拱顶角度为165°时达到最小值。填土高度大于3 m时最大等效应力随拱顶角度增大而增大，说明较小拱顶角度有利于高填方，并且，135°拱顶角度的管拱型波纹管较其它拱顶角度波纹管都具有较低的最大等效应力值。说明拱顶圆弧不是将力垂直传递到腰部圆弧连接处，而是在x轴上有有分力，并且随着拱顶角度的增加这种分力越大，但这种增加不是线性的，有一定的收敛性。

图10 最大等效应力与拱顶角度曲线Fig.10 The maximum equivalent stress of vaulting radian

4.3 钢波纹管的最大横向位移

随着填土高度的增加横向位移增大，见图11。其中拱顶角度为150°时其增长率最大，180°时增长率最小，说明横向位移的变化不是单一因素，而是拱顶弦长和x轴向分力共同作用的结果。

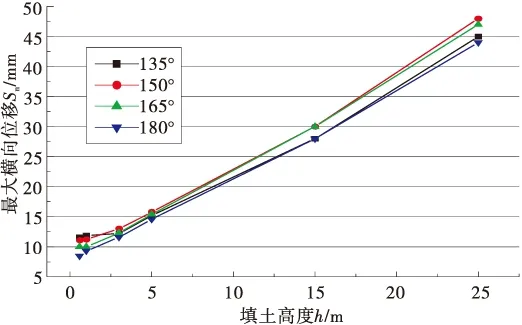
图11 最大横向位移与填土高度曲线Fig.11 The maximum lateral displacement of filling height

在填土高度小于5 m时横向位移随拱顶角度增大而减小，填土高度大于3 m时横向位移先增大后减小，在拱顶角度150°附近存在一个最大值，见图12。说明填土高度在5 m以上时拱顶弦长和x轴向分力同时作用使得拱顶角度为150°的钢波纹管横向位移最大。

图12 最大横向位移与拱顶角度曲线Fig.12 The maximum lateral displacement of vaulting radian

4.4 钢波纹管的最大竖向位移

从图13可以看出，随着填土高度的增加竖向位移呈现出先增大后减小的趋势，填土高度为1 m取得最小值。拱顶角度135°的管拱的竖向位移较其它拱顶角度的管拱更高；同时，拱顶角度165°的管拱竖向位移较其它拱顶角度的管拱更低。说明，拱顶角度165°的管拱在抵抗竖向变形方面具有优势。

一定填土高度下竖向位移随着拱顶角度变大竖向最大位移先下降后增加。可以看出，填土高度超过5 m时最大竖向位移与横向位移变化规律是相反的，见图12、图14。对于受压的波纹钢圆管，其横向直径方向增加越大竖向直径方向变化也就随着减小越大。但是从图14中却发现最大竖向位移减小。说明，拱顶竖向变形由拱顶弦长和x轴向分力两方面导致。

图13 最大竖向位移与填土高度曲线Fig.13 The maximum vertical displacement of filling height

图14 最大竖向位移与拱顶角度曲线Fig.14 The maximum vertical displacement of vaulting radian

5 结 论

1)低填方时土体等效应力在荷载处比较集中，对下部土体的影响较小。高填方时管周土体最大等效应力在腰部圆弧底部，该部位的夯实与否是影响管拱波纹管安全性的关键之一。

2) 填土高度为0.6，1.0 m的管周波谷应力表现为先减小后增大再减小的趋势。填土高度大于等于3 m管周波谷应力变化曲线较活跃。在高填方时随着节点号的增加波峰应力曲线出现两个峰值，前峰值大于后峰值。这两个“骆驼峰”峰值出现在波谷等效应力峰值的两侧位置。填土高度大于0.6 m时管拱型钢波纹管最大应力出现在腰部圆弧处，并且最大等效应力随着填土高度增大而增大。135°拱顶角度的管拱型钢波纹管在最大等效应力方面有良好的优势。

3) 随着填土高度的增加横向位移增大。在填土高度小于5 m时横向位移随拱顶角度增大而减小，填土高度大于3 m时横向位移随拱顶角度先增大后减小，在拱顶角度150°附近存在一个最大值。管拱型钢波纹管具有良好的抵抗横向变形的能力，其中拱顶角度180°钢波纹管最佳。

4) 随着填土高度的增加竖向位移呈现出先增大后减小的趋势，填土高度为1 m取得最小值。拱顶角度165°的管拱在抵抗竖向变形方面具有优势。一定填土高度下竖向位移随着拱顶角度变大竖向最大位移先下降后增加。

5) 等效应力的大小是约束钢波纹管应用的主要方面之一。钢波纹管适应地基变形的能力较强，在直径的2 %变化范围内都是允许的。所以最优管型为拱顶角度为135°的截面形式。管拱型钢波纹管在腰部易形成较大的应力值，对管拱型钢波纹管的应用具有很大的限制。比较好地解决办法就是把该部位设计成双层波纹钢板。

[1] 李萌,杨帆.上埋式管涵竖向土压力计算方法[J].桥隧机械&施工机械化,2011,28(6): 70-73. LI Meng,YANG Fan. Calculating method of vertical earth pressure for positive buried culvert[J].BridgeandTunnelMachinery&ConstructionTechnology,2011,28(6): 70-73.

[2] 李祝龙.公路钢波纹管涵洞设计与施工技术[M].北京:人民交通出版社,2007. LI Zhulong.DesignandConstructionofCorrugatedSteelCulverts[M].Beijing:China Communications Press,2007.

[3] 陈昌伟.波形钢板结构及其在公路工程中的应用[J].公路,2000(7): 48-54. CHEN Changwei.The usage and the structure of corrugated steel plate in highway engineering[J].Highway,2000(7):48-54.

[4] Purdum R L.HandBookofSteelDrainage&HighwayConstruction

Products[M].2nd ed. Kentucky, United States: The Lakeside Press, 1971.

[5] 尹航.覆土波纹钢板拱桥力学性能分析及设计方法研究[D].北京：北京交通大学，2008. YIN Hang.MechanicsBehaviorandDesignaboutBuriedCorrugatedSteelArchBridge[D].Beijing:Beijing Jiaotong University,2008.

[6] 刘百来,李祝龙,汪双杰.钢波纹管涵洞力学性能的有限元分析[J].西安工业学院学报,2006,26(1):83-86. LIU Bailai,LI Zhulong,WANG Shuangjie.The accuracy of finite element analysis about the mechanical performance of corrugated steel culvert[J].JournalofXi’anInstituteofTechnology,2006,26(1): 83-86.

[7] 刘百来,李祝龙,史永高,等.半刚性波形梁护栏受侧面碰撞的有限元仿真[J].西安工业大学学报,2007,27(3):187-290. LIU Bailai,LI Zhulong,SHI Yonggao,et al. Finite element simulation of side crashed semi-rigid guardrail of w-beam[J].JournalofXi’anTechnologicalUniversity,2007,27(3):187-290.

[8] 王艳丽,李祝龙,吴大中.钢波纹管涵洞的薄壳效应[J].公路交通科技,2008,25(5):86-90. WANG Yanli,LI Zhulong,WU Dazhong. Thin shell effect of corrugated steel culvert performance[J].JournalofHighwayandTransportationResearchandDevelopment,2008, 25(5):86-90.

[9] 李祝龙,梁养辉,黄志福，等.低路堤荷载作用下钢波纹板拱桥应变的测试研究[J].武汉理工大学学报(交通科学与工程版),2013,37(5):939-942. LI Zhulong,LIANG Yanghui,HUANG Zhifu,et al. Experimental study on strain of corrugated steel arch bridge under loader load in low embankment[J].JournalofWuhanUniversityofTechnology(TransportationScience&Engineering),2013, 37(5):939-942.

[10] 杨桂通.弹塑性力学引论[M].北京：清华大学出版社,2004. YANG Guitong.IntroductiontoElasticityandPlasticity[M].Beijing: Tsinghua University Press,2004.

[11] 骆志红.大直径钢波纹管涵有限元计算分析[J].交通科技,2011(1):40-42. LUO Zhihong. Finite element analysis of major diameter corrugated steel culvert[J].TransportationScience&Technology, 2011(1):40-42.

[12] 刘伟,汤连生,张庆华.车辆动载下路基土竖向动应力及扩散规律[J].重庆交通大学学报(自然科学版),2012,31(4):799-802. LIU Wei,TANG Liansheng,ZHANG Qinghua.Research on dynamic stress of subgrade soil under vehicle loads and its diffused rule[J].JournalofChongqingJiaotongUniversity(NaturalScience), 2012,31(4):799-802.

[13] 冯丽.考虑土-结相互作用的覆土波纹钢板圆管涵的力学性能分析[D].北京:北京交通大学,2009. FENG Li.MechanicsBehavioraboutBuriedCorrugatedSteelCulvertsConsideringSoil-structureInteraction[D].Beijing:Beijing Jiaotong University,2009.

Finite Element Analysis of Arch-shaped Steel Corrugated Tubular Culvert

LI Zhulong1,2,CAO Biao1, LIANG Yanghui2, JIANG Tao1, GUO Liyuan2

(1. School of Civil Engineering,Chongqing Jiaotong University, Chongqing 400074, P.R.China；2. CCCC Xi’an Environmental Engineering Co.,Ltd., CCCC First Highway Consultants Co.,Ltd., Xi’an 710075, Shaanxi, P.R.China)

In order to expand the application of corrugated steel tubular culvert, a computation analysis on the loading deformation of arch-shaped steel corrugated tubular culvert was carried out by a reasonable mechanical finite element model established by use of large-scaled finite element analysis software. The law of loading deformation of the arch-shaped steel corrugated tubular culvert was obtained by finite element analysis. Among the finite element models set up, the variation law of surrounding equivalent stress, maximum equivalent stress, lateral movement, vertical displacement of the arch-shaped steel corrugated tube under the forces of filling height acting on different vault radian were computed by imposing loads of rating I for highway. Thus the optimal tube shape was determined , which is practical and important and may guide the development and application of the arch-shaped steel corrugated tubular culvert.

highway engineering；arch-shaped corrugated steel tubular culvert; finite element; radian vault; filling height

10.3969/j.issn.1674-0696.2016.04.07

2015-03-19；

2015-06-20

吉林省交通厅科技计划项目(2014-4-1-11)

李祝龙(1972—)，男，江苏姜堰人，高级工程师，博士，主要从事道路工程方面的研究。E-mail：lizhulong2004@126.com。

U416.1

A

1674-0696(2016)04-029-06