一种新的自适应变异粒子群优化算法在PMSM参数辨识中的应用

黄 松, 田 娜, 纪志成,2

(1. 物联网工程学院, 江南大学， 江苏 无锡 214122； 2. 轻工过程先进控制教育部重点实验室, 江南大学， 江苏 无锡 214122)

一种新的自适应变异粒子群优化算法在PMSM参数辨识中的应用

黄 松1, 田 娜1, 纪志成1,2

(1. 物联网工程学院, 江南大学， 江苏 无锡 214122； 2. 轻工过程先进控制教育部重点实验室, 江南大学， 江苏 无锡 214122)

高精度辨识永磁同步电机参数是进行控制器设计的基础。本文借鉴遗传算法中变异操作的思想，提出了一种基于自适应变异概率的混合变异粒子群优化算法，并将其应用于永磁同步电机参数辨识问题。本文首先在dq坐标系下建立永磁同步电机参数辨识模型，然后将该算法和几种变异粒子群算法用于永磁同步电机参数辨识，并在Matlab/Simulink中进行了对比验证。实验结果表明，该算法能提高定子电阻、d轴电感、q轴电感和转子磁链等参数的辨识精度，为提高永磁同步电机电机控制器性能提供了保证。

粒子群算法; 变异概率; 永磁同步电机; 参数辨识

1 引言

永磁同步电机(PMSM)广泛用于柔性制造系统、风力发电和精密伺服系统等。但是，它的物理参数容易受到温度、定子电流和磁通饱和等因素的影响，获得准确可靠的物理参数是永磁同步电机系统稳定可靠运行的关键。精确的电机参数和先进的控制思想是设计电机控制器的基础，电机参数准确程度直接影响控制器控制性能的好坏。因此，需要研究相应的辨识算法来估计准确的电机参数信息。

将递推最小二乘法[1]、扩展卡尔曼滤波器法[2]和神经网络辨识方法[3]等传统方法应用于电机参数辨识时，需要对电机模型进行复杂的变换，因此，这些方法对具有非线性时变特征的参数和多参数的辨识还相当困难。近年来，许多智能优化算法如蚁群算法、遗传算法和粒子群算法等[4-7]被引入到电机参数辨识中，取得了很好的效果。文献[4]将粒子群算法用于感应电机的参数辨识中，仿真证明粒子群算法的辨识精度比蚁群算法更高。文献[5]提出了平均最好位置和柯西变异相结合的改进粒子群算法，对永磁同步电机定子绕组的电阻、电感和磁链进行辨识，实验证明该辨识方法搜索精度高，稳定性好。文献[6]提出了一种双模态自适应小波粒子群的永磁同步电机多参数识别与温度监测方法。文献[7]提出用蚁群矢量移动算法同时辨识永磁同步电动机负载运行时的转动惯量和负载转矩。

本文介绍了一种新的自适应变异概率的混合变异粒子群优化算法，并将其应用于PMSM的参数辨识。本文首先建立了永磁同步电机的非线性参数模型，采用矢量控制的永磁同步电机得到电机实际电压电流数据，利用新的自适应变异概率的混合变异粒子群优化算法辨识了电机模型的定子绕组电阻、dq轴电感和永磁磁链等参数。

2 PMSM数学模型

2.1 PMSM模型

本文中忽略 PMSM 的磁场饱和、铁损和涡流损耗，PMSM dq坐标系的电压方程和磁链方程分别为：

(1)

(2)

式中，ud、uq为d,q轴上的电压分量；id、iq为d,q轴上的电流分量；ψd、ψq为d,q轴上的磁链；R为定子绕组电阻；Ld、Lq为d,q轴上的等效电枢电感；ψf为永磁铁产生的磁链；υ为电气角度转速；在PMSM模型中，p={R,Ld,Lq,ψf}是需要辨识的参数。

当id=0时，对dq轴电流进行解耦，使定子电流只有q轴交流分量，在电机电流处于稳态时，将式(2)代入式(1)并进行离散化可得：

(3)

由于有四个参数需要辨识，在电机电流稳态时通过在短时间内注入一个id≠0的d轴电流，得到另一个二阶电机dq轴模型为：

(4)

综合式(3)和式(4)，得到一种四阶PMSM电机dq轴辨识模型为：

(5)

则构造PMSM辨识模型的适应度函数如下：

(6)

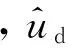
2.2 矢量控制方法

本文中采用id=0的控制方法对永磁同步电机进行控制。该控制策略可实现dq轴电流解耦。图1为永磁同步电机矢量控制框图。

图1 永磁同步电机矢量控制图Fig.1 Diagram of vector control on PMSM

3 基本粒子群算法

粒子群算法是由美国心理学家Kennedy和电气工程师Eberhart博士在1995年提出的。该算法通过定义带有速度和位置的粒子来搜索问题空间，通过种群中粒子的个体最优位置和全局最优位置指导下一代粒子速度和位置的更新, 使种群收敛于全局最优位置。基本粒子群算法的速度和位置公式如下:

(7)

(8)

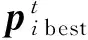
在本文中, 选用现在比较常用的线性惯性权重更新公式：

w=wmax-t(wmax-wmin)/M

(9)

式中，wmax、wmin分别表示惯性权重取值的上下限；M为总迭代次数；本文中,wmax、wmin分别取值为0.9、0.4。

4 自适应变异概率的混合变异粒子群算法(AMPSO)

4.1 自适应变异概率和全局最优混合变异

(10)

(11)

式中，α用来调节变异概率变化快慢, 为一常数, 取值范围为[2, 4]。

gbest=pg(1+0.5randn)

(12)

柯西变异公式为：

Cauchy=tan(π(rand-0.5))

(13)

gbest=pg(1+0.5Cauchy)

(14)

式中，pg表示全局最优位置和全局次优位置中随机的一个；Cauchy为柯西分布的随机数。

全局最优混合变异策略(mut1)的伪代码如下：

Begin

Obtainthebestpositiongbest

and the second best positionpsec

Ifrand<0.5

pg=gbest

Else

pg=psec

End

gbest=pg*(1+0.5*randn);

End

Cauchy=tan(π*(rand-0.5));

gbest=pg*(1+0.5*Cauchy);

End

End

4.2 最差个体最优的自适应小波变异

在4.1节所述混合变异策略中，利用了全局最优和次优极值进行变异，而没有利用较差个体最优。在种群中，较差个体最优对粒子的指导作用有限，因而，对较差个体最优进行变异有利于加快群体的收敛速度。本文采用自适应小波变异来改进最差个体最优，从而加快群体的进化速度。其母波函数为:

(15)

本文选择 Morlet 小波, 公式如下:

(16)

小波幅值ψ(x)随着参数a的增加而不断地减少,为了自适应调节小波幅值ψ(x)，本文提出自适应参数a，其表达式为:

a=kt+a0

(17)

式中,k和a0为正常数,文中k设定为10,a0设定为 5。

求出最差个体m第j维的个体最优位置pmjbest，最差个体最优的自适应小波变异策略(mut2)如式(18)和式(19)所示：

(18)

(19)

4.3 AMPSO算法辨识PMSM参数的实现

在PMSM模型中，p={R,Ld,Lq,ψf}是需要辨识的参数，将其设置为粒子的位置，AMPSO算法辨识PMSM模型参数的实现步骤如下：

(1) 初始化粒子群算法参数(每个粒子速度和位置)，根据公式(5)求出理想的dq轴电压{ud0,uq0,ud,uq}，计算PMSM辨识模型的适应度函数f(p)，求出pibest和gbest。

(2) 判断算法是否满足停止条件, 是, 执行步骤(6)；否, 执行步骤(3)～步骤(5)。

(3) 根据式(7)～式(9)更新粒子的速度和位置。

(4) 根据4.1节和4.2节的变异策略mut1和mut2进行变异。

(5)根据式(5)求出理想的dq轴电压{ud0,uq0,ud,uq}，计算PMSM辨识模型的适应度函数f(p)，更新pibest和gbest。

(6) 输出最优的辨识参数p={R,Ld,Lq,ψf}和最优适应值f(p)， 算法运行结束。

5 实验验证与结果分析

5.1 实验设置

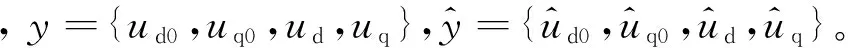
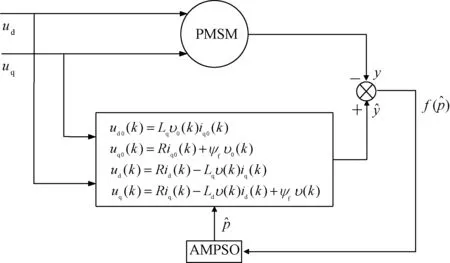
图2 永磁同步电机多参数辨识模型Fig.2 Multiple parameter identification model on PMSM

表2 五种PSO算法的适应值比较Tab.2 Fitness comparison among five PSO variants on PMSM

表3 五种PSO算法的 PMSM 参数辨识结果比较Tab.3 Parameter results comparisons among five PSO variantson PMSM

本文借鉴了其他四种算法来进行对比，四种算法分别为耗散粒子群优化算法(DPSO)[8]、自组织分层粒子群优化算法(HPSO)[9]、微分进化混合粒子群优化算法(MPSO)[10]和速度差分变异粒子群优化算法(VDMPSO)[11]。实验参数设置如下： 种群规模均为30，w=0.7、c1=c2=2、α=3。为了减少实验统计误差，所有实例独立运行20次，最大迭代次数为100。

表1 电机设计参数Tab.1 Design parameters of PMSM

5.2 试验结果与分析

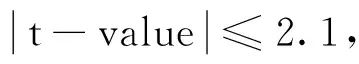
从表2中可知，AMPSO算法优化的适应值的平均值、最大值、最小值、方差和t-value值均优于DPSO、HPSO、MPSO和VDMPSO，证明AMPSO算法对PMSM参数辨识效果要好于其他四种算法。从平均消耗时间来看，AMPSO算法和其他四种算法相比没有明显优势。从表3中可知，AMPSO算法辨识电机参数的平均值、方差和t-value值的绝对值均比其他四种算法小，说明AMPSO算法对PMSM多参数辨识精度稳定性高，辨识结果与真实值无明显差异，具有98%的置信度。

图3为PMSM多参数辨识模型适应值收敛曲线，图4～图7为参数辨识过程的收敛曲线。

图3 PMSM 多参数辨识模型适应值收敛曲线Fig.3 Fitness convergence curves of five PSOs on parameter identification model of PMSM

图4 PMSM电机绕组电阻辨识曲线Fig.4 Winding resistance identification curves of five PSOs on PMSM

图5 PMSM d轴电感辨识曲线Fig.5 d inductance identification curves of five PSOs on PMSM

图6 PMSM q轴电感辨识曲线Fig.6 q inductance identification curves of five PSOs on PMSM

图7 PMSM永磁磁链辨识曲线Fig.7 Rotor flux identification curves of five PSOs on PMSM

图4～图7中纵轴分别代表五种算法对PMSM的绕组电阻、d轴电感、q轴电感和永磁磁链的计算结果。从图3～图7可以看出，AMPSO算法解决PMSM参数辨识问题的收敛精度有明显提高。

6 结论

本文针对PMSM参数辨识问题，提出了一种自适应变异概率的粒子群算法。针对永磁同步电机多参数辨识问题， AMPSO能够准确地辨识出永磁同步电机定子电阻、d轴电感、q轴电感和永磁磁链，在电机参数辨识中具有良好的性能。通过仿真实验，证明该方法对PMSM参数辨识具有精度高、稳定性好的特点。

[1] 何晋伟, 史黎明(He Jinwei, Shi Liming). 一种基于静态特性的直线感应电机参数辨识方法(An identification method for linear induction motor parameter based on static characteristics)[J]. 电工电能新技术(Advanced Technology of Electrical Engineering and Energy), 2009, 28(4):50-53.

[2] Bolognani S,Tubiana L,Zigliotto M. Extended Kalman filter tuning in sensorless PMSM drives[J].IEEE Transactions on Industry Applications, 2003, 39(6): 1741-1747.

[3] 汪镭, 周国兴, 吴启迪(Wang Lei, Zhou Guoxing, Wu Qidi). 神经网络辨识方案在异步电机传动系统参数辨识中的应用讨论(Application of Hopfield neural network in asynchronous motor parameters’ identification)[J]. 电工电能新技术(Advanced Technology of Electrical Engineering and Energy), 2001, 20(2):58-63.

[4] 陈振锋，钟彦儒，李洁(Chen Zhenfeng, Zhong Yanru, Li Jie). 感应电机参数辨识三种智能算法的比较(Comparison of three intelligent optimization algorithms for parameter identification of induction motors)[J]. 电机与控制学报(Electric Machines and Control), 2010, 14(11):7-12.

[5] 傅小利，顾红兵，陈国呈，等(Fu Xiaoli, Gu Hongbing, Chen Guocheng, et al.). 基于柯西变异粒子群算法的永磁同步电机参数辨识(Permanent magnet synchronous motors parameters identification based on Cauchy mutation particle swarm optimization)[J]. 电工技术学报(Transactions of China Electrotechnical Society), 2014, 29(5):127-131.

[6] 刘朝华，周少武，刘侃，等(Liu Zhaohua, Zhou Shaowu, Liu Kan, et al.). 基于双模态自适应小波粒子群的永磁同步电机多参数识别与温度监测方法(Permanent magnet synchronous motor multiple parameter identification and temperature monitoring based on binary-modal adaptive wavelet particle swarm optimization)[J]. 自动化学报(Acta Automatica Sinica), 2013, 39(12):2121-2130.

[7] 王少威，万山明，周理兵，等(Wang Shaowei, Wan Shanming, Zhou Libing,et al.). 利用蚁群算法辨识PMSM伺服系统负载转矩和转动惯量(Identification of PMSM servo system’s load torque and moment of inertia by ant colony algorithm)[J]. 电工技术学报(Transactions of China Electrotechnical Society), 2011, 26(6):18-25.

[8] Xie X F, Zhang W J, Yang Z L. A dissipative particle swarm optimization[A]. Proceedings of the IEEE International Conference on Evolutionary Computation [C]. Honolulu, USA,2002.1456-1461.

[9] Ratnaweera A, Halgamuge S, Watson H C. Self-organizing hierarchical particle swarm optimizer with time-varying acceleration coefficients[J]. IEEE Transactions on Evolutionary Computation, 2004, 8(3):240-255.

[10] Zhang W J, Xie X F. DEPSO: Hybrid particle swarm with differential evolution operator[A]. Proceedings of IEEE International Conference on System, Man and Cybernetics [C]. Washington D C, USA, 2003.3816-3821.

[11] 江善和，王其申，江巨浪(Jiang Shanhe, Wang Qishen, Jiang Julang). 一种速度差分变异的粒子群优化算法(Particle swarm optimization algorithm based on velocity differential mutation)[A]. 中国控制与决策会议(Chinese Control and Decision Conference) [C]. 2009. 1860-1865.

Study of PMSM parameter identification using particle swarm optimization with adaptive mutation probability

HUANG Song1, TIAN Na1, JI Zhi-cheng1,2

(1. School of Internet of Things Engineering, Jiangnan University, Wuxi 214122, China; 2. Key Laboratory of Advanced Process Control for Light Industry, Ministry of Education, Jiangnan University, Wuxi 214122, China)

Permanent magnetic synchoronous motor (PMSM) is a kind of strong nonlinear dynamic system.The identification of the parameters in PMSM is the foundation for the design of its controller. The parameter identification problem of PMSM presents excessive complexity due to the intercoupling of parameters. It is hard to obtain high precision estimated parameter values using the conventional method and no effective approach has been developed to identify five parameters of PMSM precisely and rapidly to date. In this paper, inspired by the idea of mutation operator in genetic algorithm, an adaptive mutation probability and hybrid mutation strategy is introduced to particle swarm optimization and then applied to parameter identification model of PMSM. Firstly, parameter identification model of PMSM is established under the dqcoordinateandthencomparedwithseveralmutationPSOsinMatlab/Simulink.Experimentalresultsshowthatthisalgorithmisabletoimprovetheidentificationaccuracyofstatorresistance, dinductance, qinductance,rotorfluxandsoon,guaranteeingthecontrollerperformanceofPMSM.

particle swarm optimization; mutation probability; PMSM; parameter identification

2015-03-04

国家自然科学基金 (61572238)、 国家高技术研究发展计划 (2014AA041505) 资助项目

黄 松(1984-)， 男， 湖北籍， 博士研究生， 从事电力电子与电机控制的研究； 田 娜(1983-)， 女， 河北籍， 博士后， 从事智能算法和智能控制技术的研究。

TP18;TM

A

1003-3076(2016)06-0067-07