永磁同步电机控制参数设计方法

邱腾飞， 温旭辉， 赵 峰， 王永兴

(1. 中国科学院电工研究所， 北京 100190; 2. 中国科学院大学, 北京 100049; 3. 中国科学院电力电子与电气驱动重点实验室， 北京 100190; 4. 电驱动系统大功率电力电子器件封装技术北京市工程实验室， 北京 100190)

永磁同步电机控制参数设计方法

邱腾飞1,2， 温旭辉1,3,4， 赵 峰1,3,4， 王永兴1,3,4

(1. 中国科学院电工研究所， 北京 100190; 2. 中国科学院大学, 北京 100049; 3. 中国科学院电力电子与电气驱动重点实验室， 北京 100190; 4. 电驱动系统大功率电力电子器件封装技术北京市工程实验室， 北京 100190)

磁场定向控制(FOC)由于其良好的解耦性、较小的转矩脉动和容易实现等优点，成为最广泛使用的永磁同步电机控制方法。电流环参数设计是磁场定向控制的关键。本文通过对电流环进行分析，采用传递函数分析的方法，在考虑交叉耦合的条件下推导控制参数与电流控制性能的关系，给出控制参数的优化选取原则。

永磁同步电机； PI参数设计； 矢量控制

1 引言

永磁同步电机(PMSM)具有高转矩/惯量比、高功率密度、高效率、体积小、响应快、运行可靠等优点，近年来在电动汽车上的应用越来越普及[1,2]。

由于永磁同步电机数学模型具有多变量、强耦合以及非线性等特点，所以控制较为复杂。交流电机在同步旋转坐标系上的电流id、iq之间存在耦合，在负载变化时，耦合项将影响 dq 轴电流响应，恶化电机转矩响应速度[3]。磁场定向控制(FOC)由于其良好的解耦性、 较小的转矩脉动和容易实现等优点，成为最广泛使用的永磁同步电机控制方法[4]。基于FOC，有多种弱磁控制策略，其中电压调节法由于不依赖参数，简单易行，成为实际应用中的首选。

本文通过对电流环进行分析，采用传递函数分析的方法，在考虑交叉耦合的条件下推导控制参数与电流控制性能的关系，给出控制参数的优化选取原则。

2 PMSM矢量控制

永磁同步电机坐标定义如图1所示。两相静止坐标系中的α轴与三相坐标系中的A轴重合。两相旋转坐标系的d轴与电机转子N极重合，且随着转子以ωe的角频率同步旋转。

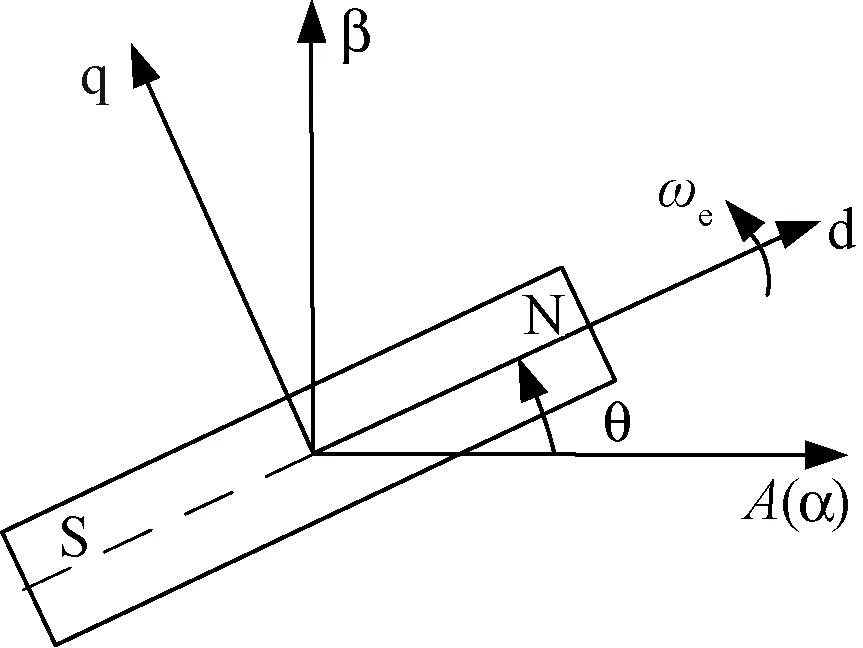
图1 PMSM坐标系定义Fig.1 Definition of coordinate system

在两相旋转坐标系下，电机电压方程可以表示为:

(1)

式中，R为定子电阻；λf为永磁体磁链；ud、uq为dq轴定子电压；id、iq为dq轴定子电流；Ld、Lq为dq轴定子电感。

PMSM的电磁转矩可表示为[5]：

(2)

式中，p为电机极对数。

根据式(1)可知，PMSM是一个多变量、强耦合、非线性的系统。经过坐标变换，可以将电机定子电流解耦为励磁电流分量和转矩电流分量，通过分别控制电机dq轴电流即可实现对电机转矩的控制[6]。PMSM矢量控制框图如图2所示。当分别给定dq轴电流指令后，矢量控制系统通过两个PI调节器实现dq电流的独立控制。

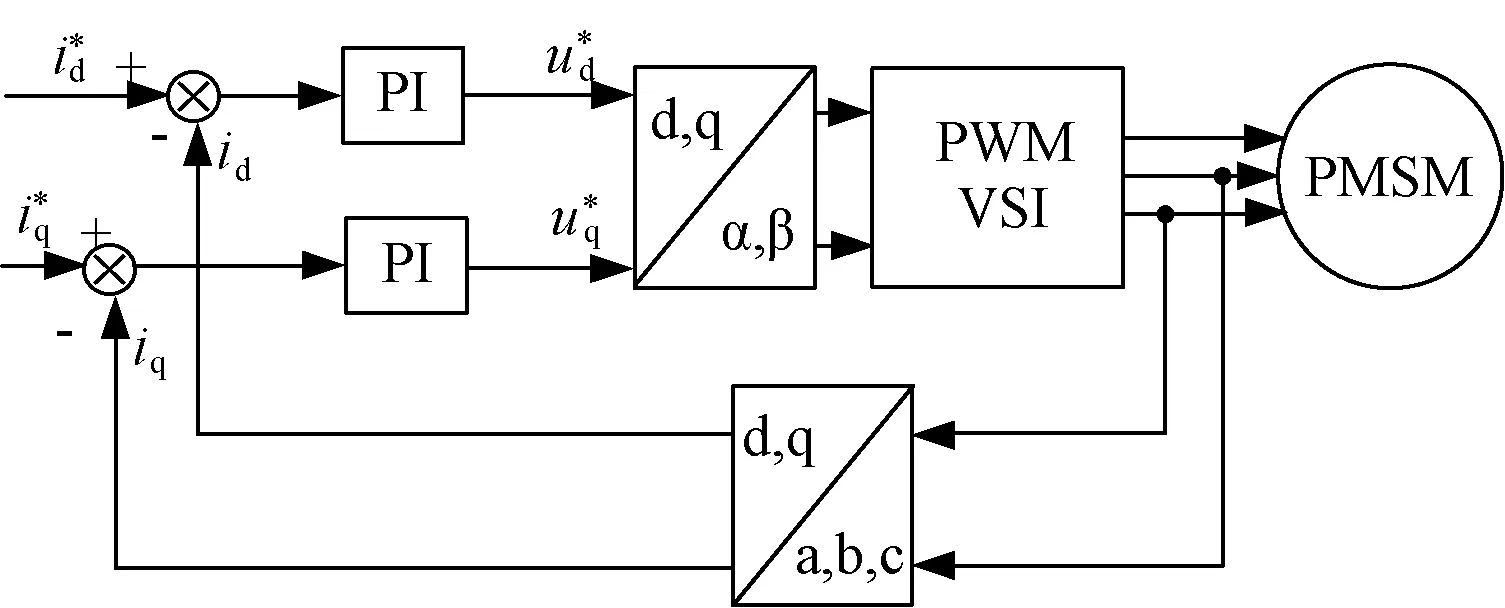
图2 PMSM矢量控制框图Fig.2 Vector control system of PMSM

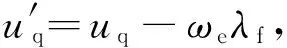
(3)

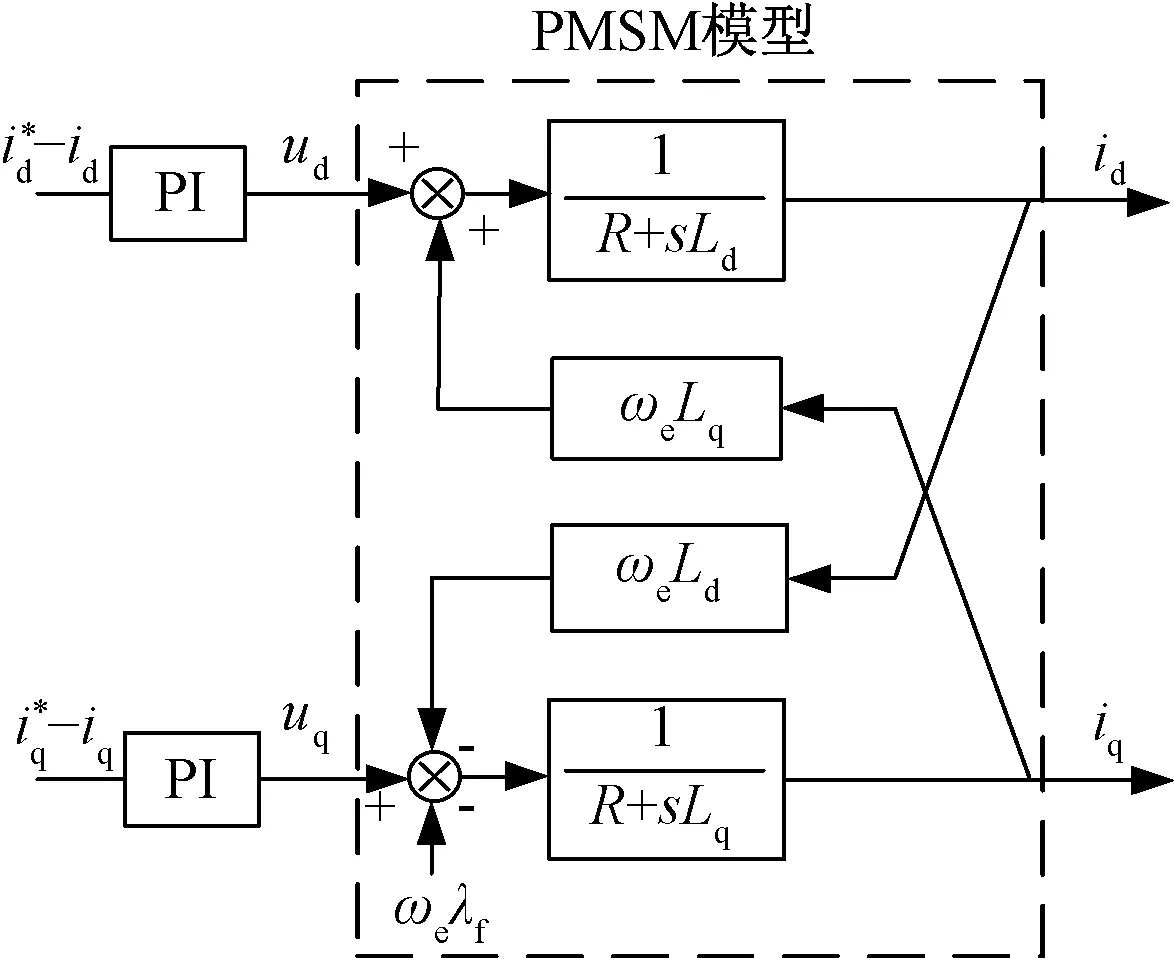
图3 永磁同步电机电流环传递函数框图Fig.3 Transfer function block diagram of PMSM

根据式(3)可将dq轴电流表示为电压及电机参数的函数：

(4)

Pm(s)=s2LdLq+R(Ld+Lq)s+R2+ωeLdLq

(5)

dq轴电压由电流误差经过PI调节器产生，有

(6)

式中，kpd和kpq分别为dq轴PI调节器比例系数；kid和kiq分别为dq轴PI调节器积分系数。

结合式(4)和式(6)可以得出电流环闭环传递函数矩阵：

(7)

式中

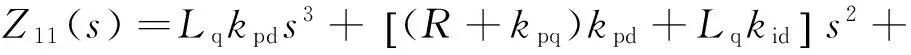
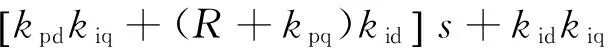
Z12(s)=ωeLq(kpds2+kids)

Z21(s)=-ωeLd(kpqs2+kiqs)

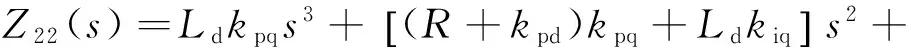
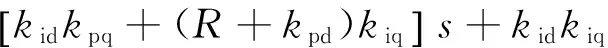
P(s)=LdLqs4+(LdR+LqR+Ldkpq+Lqkpd)s3+

(Rkid+Rkiq+kidkpq+kiqkpd)s+kidkiq

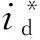
3 电流环控制参数设计

3.1 交叉耦合影响因素分析

dq电流间的交叉耦合的存在，降低了电流环控制性能，增加了PI参数的设计难度。本节通过分析电流环传递函数矩阵，推导出PI参数对交叉耦合效应的影响，进而得出以降低交叉耦合为目标的PI参数设计依据。

电机参数如表1所示。根据表1参数绘制出电机在不同转速时的幅频特性曲线，如图4所示。其PI控制参数分别为：kpd=kpq=2，kid=kiq=50。下面将对图4的结果作具体分析。

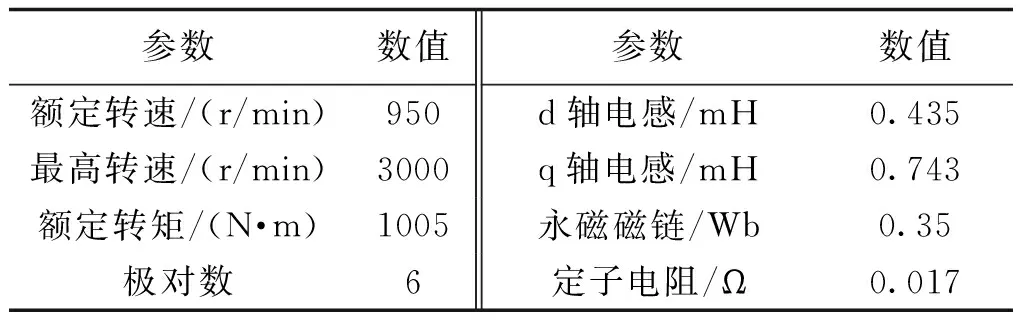
表1 电机参数Tab.1 Specifications of tested PMSM

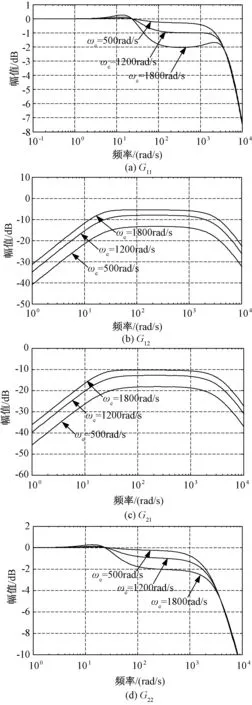
图4 不同转速时的系统波特图(kpd=kpq=2，kid=kiq=50)Fig.4 Bode plot of PMSM with different speeds(kpd=kpq=2，kid=kiq=50)

在低频段(ωe<10rad/s)，有

(8)

式(7)可近似简化为：

(9)

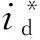
在中频段(10rad/s<ωe<103rad/s)，由于|G12|和|G21|将随着转速的增加而增大，因而交叉耦合的影响将随着转速的增加而更加明显。G12和G21在中频段的带通特性，表明电机dq轴电流在动态过程中更容易受到交叉耦合的影响。此外，G11和G22在中频段的增益将随着转速的增加而降低，这将进一步恶化dq轴电流的动态控制能力。

(10)

(11)

(12)

分析式(11)和式(12)可知，耦合函数的最大值将随着转速的升高而增大，即系统交叉耦合将随着转速的升高而增加。ki参数不影响系统的交叉耦合程度，而增大kp参数可以降低系统的耦合程度，使系统能够具有较高的抗耦合能力。

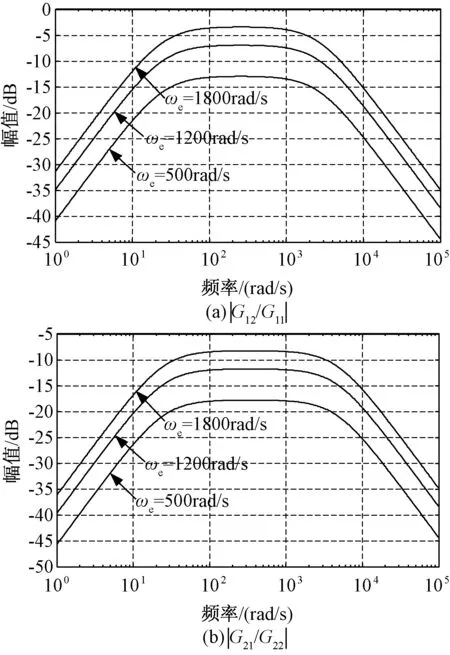
图5 不同转速时的耦合函数幅频响应Fig.5 Bode plot of coupling function

3.2 系统带宽

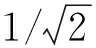
为便于求解系统带宽，可将式(7)进行简化。简化后的系统传递函数应和原函数保持相同的高频特性。忽略分子分母中的低次分量，G11和G22可简化为：

为验证简化的有效性，可分别绘制出简化前后的波特图，如图6所示。当ω>500rad/s时，简化前后的曲线基本重合，表明该简化方法可以用于分析系统的带宽。对式(13)和(14)求解，可得到函数G11和G22的带宽如式(15)所示。

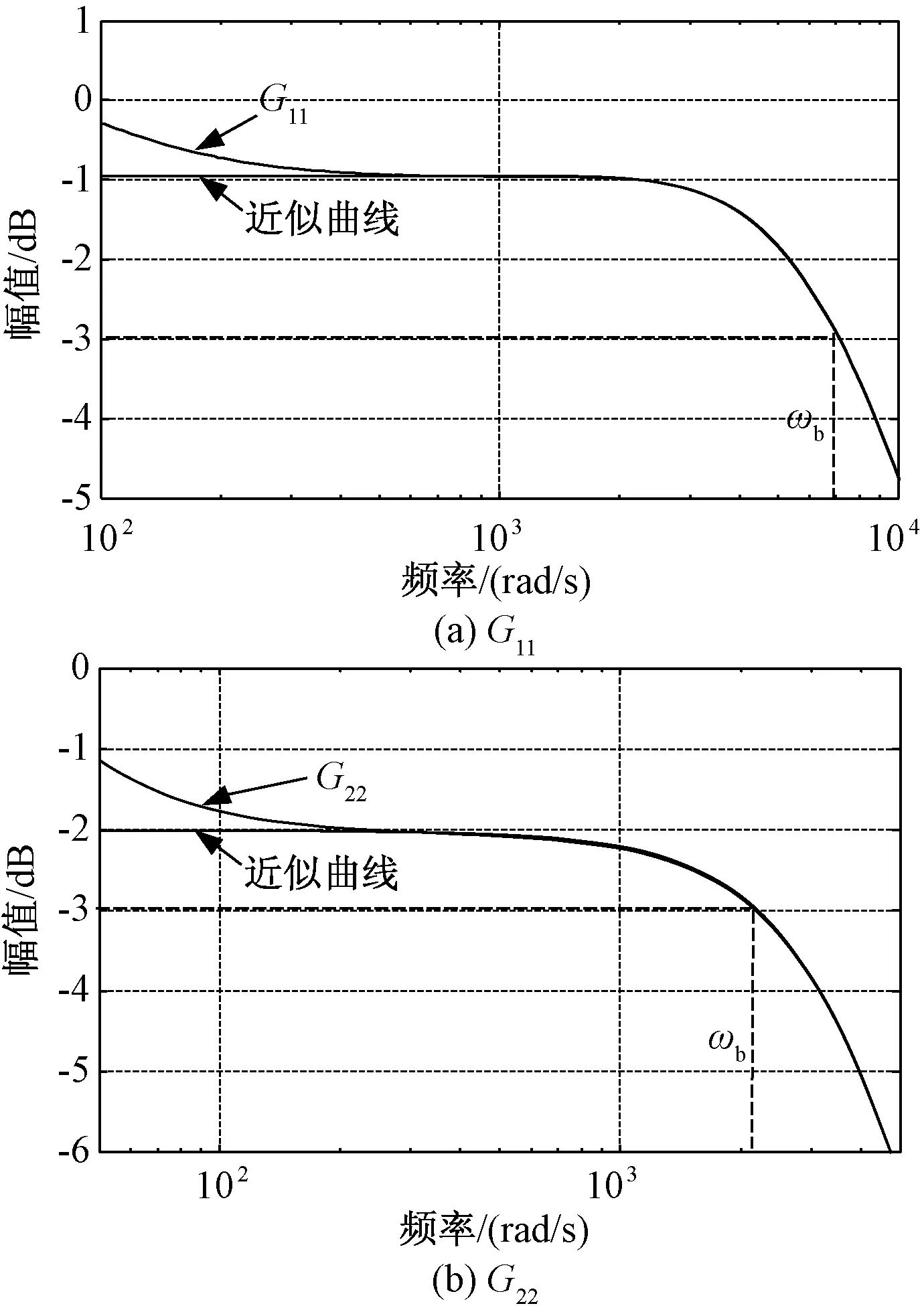
图6 高频段传递函数近似结果Fig.6 Bode plot of high-frequency section

(15)

式中

(16)

由式(15)可知，系统带宽将受到kp和ωe的影响，而不受ki的影响。根据图4可知，ωe并不改变系统带宽，因而可认为系统带宽仅受kp参数的影响。改变kp参数，可得到系统带宽的变化规律，如图7所示，该图为控制系统带宽设计提供了参数选择依据。由图7可知，G11的带宽主要受到kpd的影响而受kpq的影响较小；同样，G22的带宽主要受到kpq的影响而受kpd的影响较小。

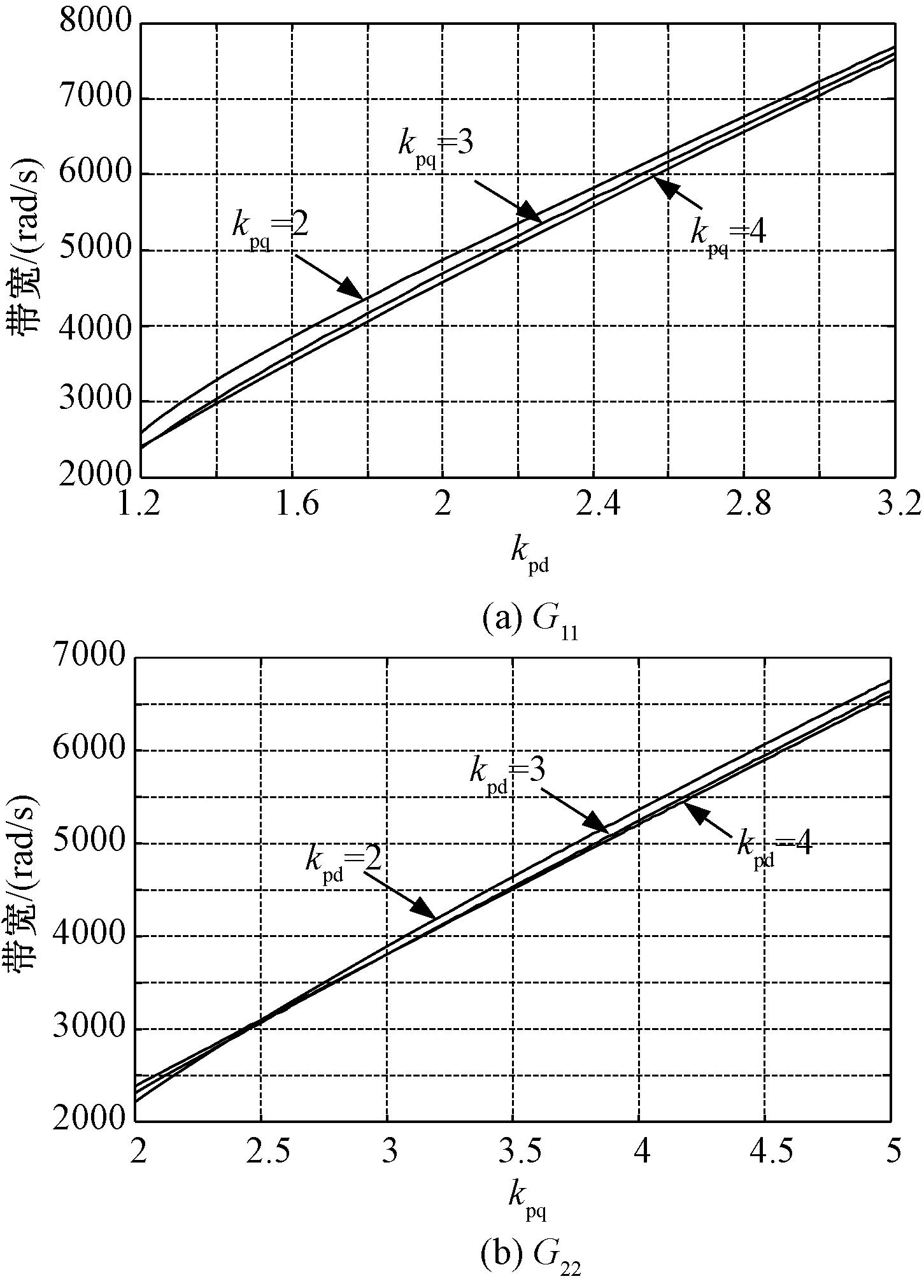
图7 系统带宽随Kp变化规律Fig.7 Bandwidth of PMSM with different speeds

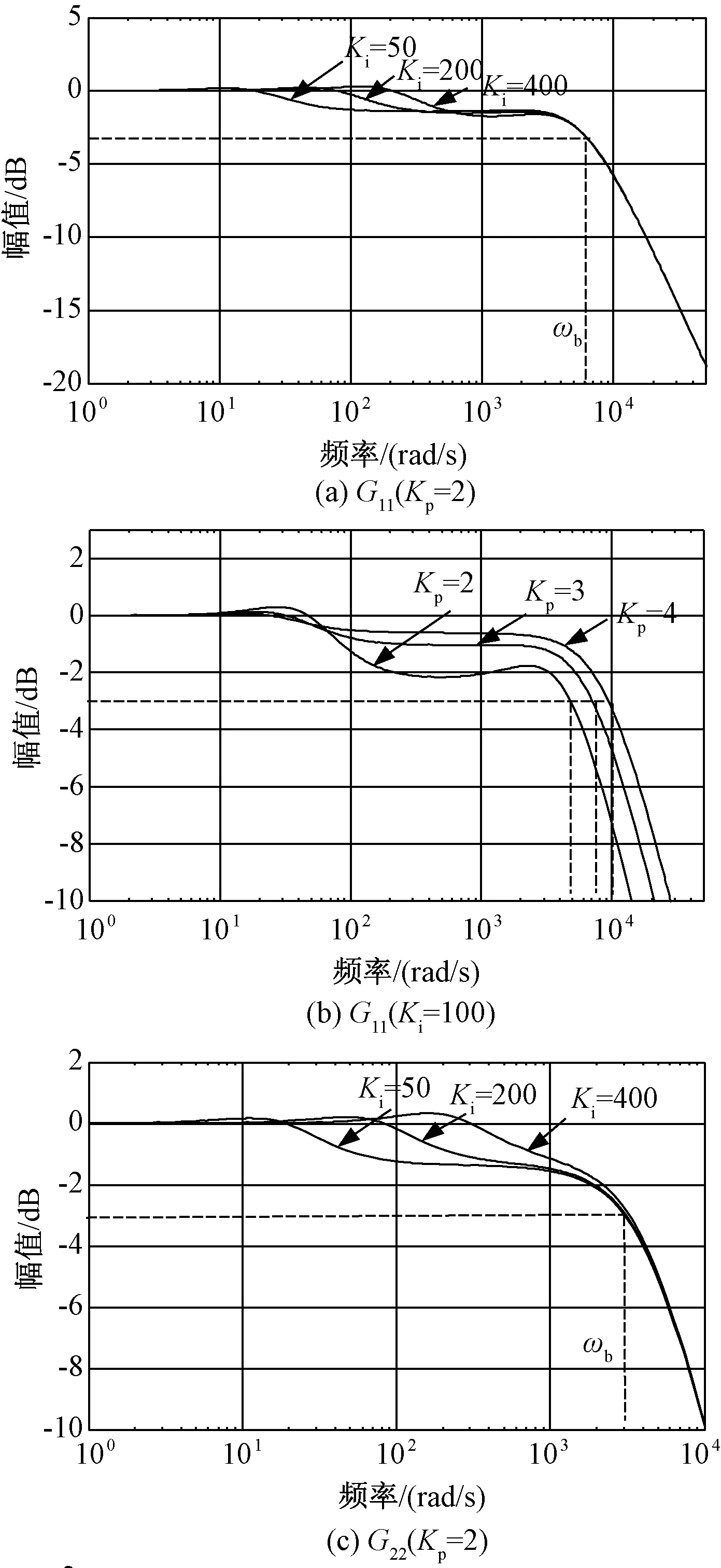
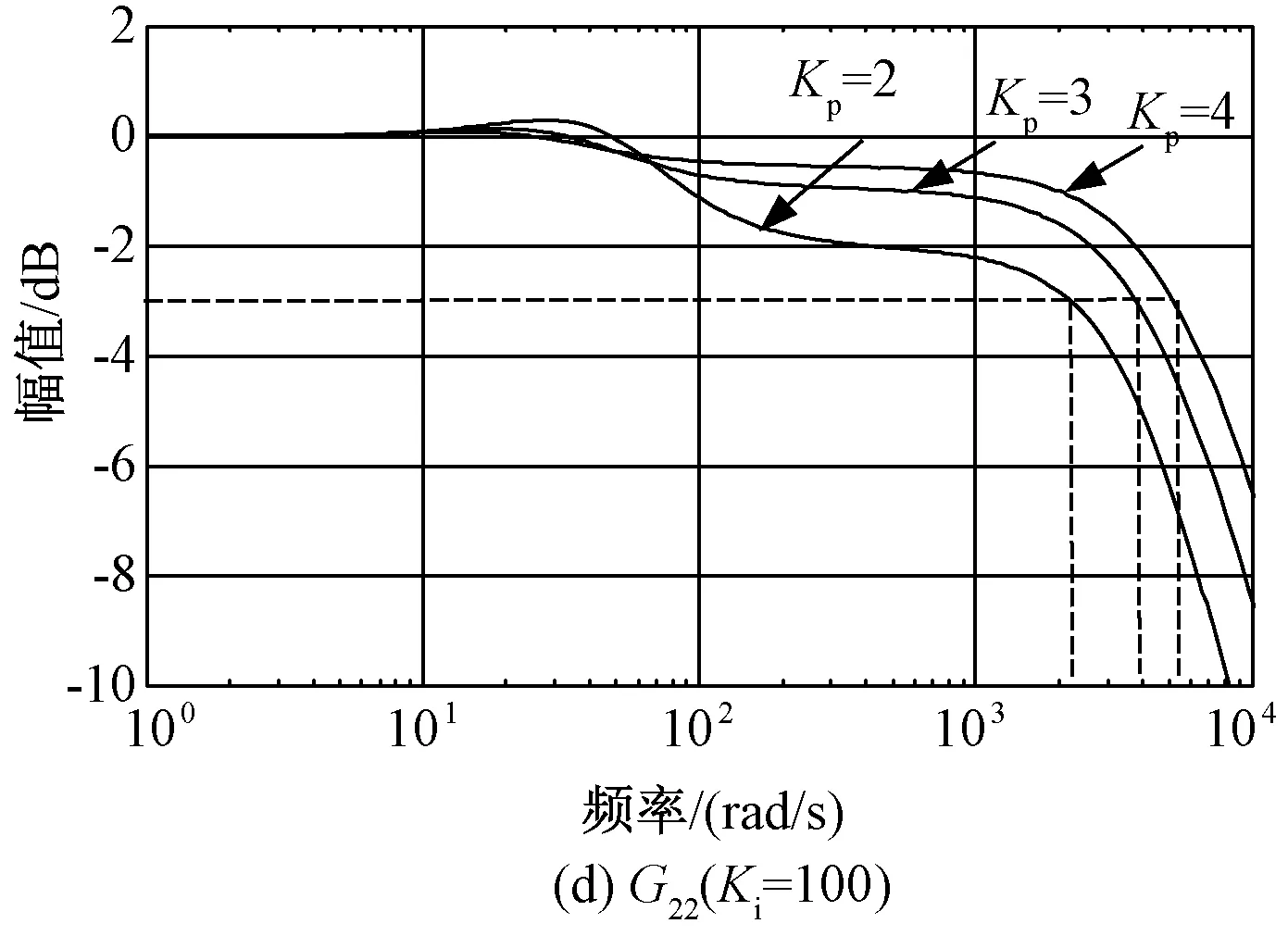
图8 不同PI参数对系统带宽的影响Fig.8 Bandwidth of PMSM with different PI parameters

改变不同的PI参数，可绘制出系统幅频特性，如图8所示。为简化分析，令kpd=kpq=Kp，kid=kiq=Ki。由图8可知，当保持Kp不变时，Ki参数的变化并不改变系统带宽；随着kp的增大，系统带宽将逐渐增加。

选择ωb时，既要满足系统高动态性能，又要考虑到高频干扰的抑制，尤其是抑制PWM开关频率的干扰。假设开关频率是5kHz，系统带宽可选定为ωb=5000rad/s。

3.3 中频段衰减

分析图4可知，G11和G22幅值在中频段(10rad/s<ω<103rad/s)将产生衰减，且衰减幅值随着转速的升高而增大。中频区衰减虽然未影响系统带宽，但是将降低系统的动态跟踪能力。本节将针对中频段衰减进行研究，分析其产生的原因及影响因素。

为便于分析，可将式(7)进行简化，简化后的传递函数应和原函数保持相同的中频段特性。G11和G22可简化为：

(17)

为验证简化的有效性，可分别绘制出简化前后的波特图，如图9所示。当10rad/s<ω<103rad/s时，简化前后的曲线基本重合，表明该简化方法可以用于分析系统的中频段衰减。

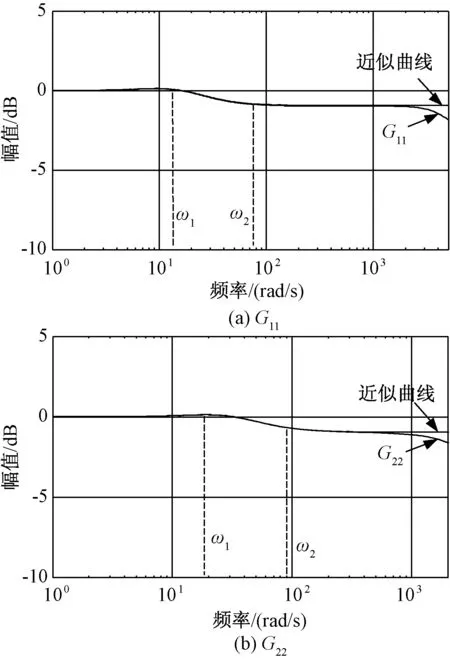
图9 中频段传递函数近似结果Fig.9 Bode plot of medium-frequency section

式(17)所示的传递函数可以看作二阶微分环节和二阶积分环节的串联。根据自动控制原理，系统波特图将在两个特征频率点处出现转折，特征频率点如式(18)和式(19)所示。在ω2>ω>ω1区间，幅频曲线将以-40dB/dec的斜率下降，即产生中频段衰减；当ω>ω2时，由于二阶微分环节的作用，幅频曲线将逐渐与横坐标平行。

(18)

(19)

(20)

式中，ω1和ω2为特征频率；ζ为阻尼系数。

为降低中频段衰减的影响，应尽量使ω1和ω2向右移动。由式(18)和(19)可知，在保持系统带宽不变 (即kp保持不变) 的条件下，应尽量增大ki参数。但是由式(20)可知，ki参数过大而kp较小时，将导致系统阻尼系数过小，从而导致系统出现振荡。为保证系统稳定，选择ζ=0.9。

分析图8可得出PI参数对中频段增益的影响。由图8(a)为例，当ki较小时，系统中频段衰减较大；随着ki参数的增大，系统中频段增益逐渐增加。但当ki过大而导致阻尼系数过小时，系统将出现较高的谐振峰值。

4 仿真验证

按照3.2节的设计方法选取ωb=5000rad/s,ζ=0.9，可计算得到PI参数分别为：kpd=2.2，kpq=3.7，kid=kiq=200。利用设计得到的参数可绘制出系统波特图，如图10所示。对比图4和图10可知，优化后的dq轴系统带宽均为5000rad/s；G12和G21的最高幅值由-5dB降低至-10dB，表明系统交叉耦合得到抑制；系统中频衰减由-2dB提高至-1dB，系统动态性能得到提升。

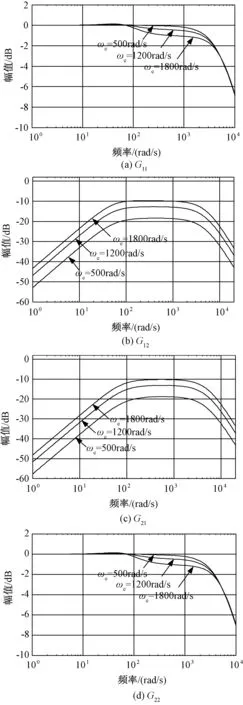
图10 不同转速时的系统波特图(kpd=2.2， kpq=3.7，kid=kiq=200)Fig.10 Bode plot of PMSM with different speeds(kpd=2.2， kpq=3.7，kid=kiq=200)

5 实验验证

图11为不同PI参数时的电流阶跃实验结果。实验中电机转速为3000r/min，dq轴电流指令在0.2s时刻均发生100A的突变。由于系统带宽和中频段增益的提高，图11(b)所示的电流响应速度明显优于图11(a)。

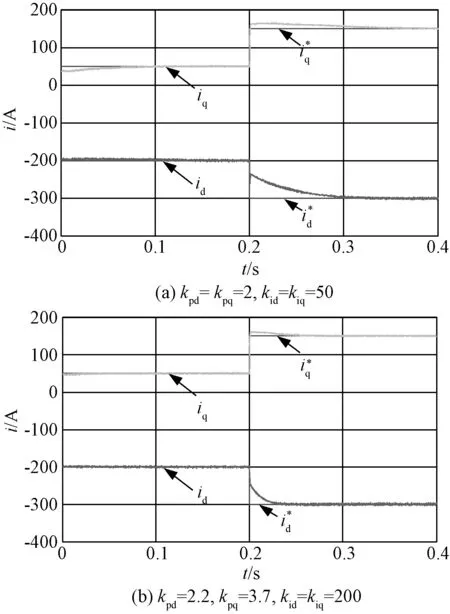
图11 不同PI参数时的电流阶跃波形Fig.11 Simulation results in current transient state

6 结论

本文通过对PMSM传递函数的分析，得出了PI参数选取的依据。与已有文献不同，本文采用了多输入多输出系统的分析方法，利用一个2×2矩阵实现了电机系统的数学描述。该模型具有更高的准确性，同时能够体现系统的交叉耦合效应。PI参数设计原则如下：

(1)系统交叉耦合程度与电机转速成正比，与kp参数成反比。因此，为了降低交叉耦合，应尽量增大kp参数。

(2)系统带宽与kp参数成正比，但不受ki参数和转速的影响。通过选择kp参数可使系统得到合理的带宽，从而保证系统的动态性能。

(3)随着转速的升高，系统传递函数将在中频段产生衰减。通过提高系统ki参数可以降低中频衰减进而提高系统的动态性能，但是过高的ki参数将使传递函数产生较大的谐振峰值，从而引起系统振荡。

[1] 中国电工技术学会电动车辆专业委员会(Electrical Vehicle Committee，China Electrotechnical Society). 我国电动汽车市场化进程中相关问题综述(Annual report on technical and industrial development of electric vehicle power supply and drive in China) [J]. 电工电能新技术(Advanced Technology of Electrical Engineering & Energy), 2015, 34(7): 1-10.

[2] Pillay P, Krishnan R. Modeling, simulation, and analysis of permanent-magnet motor drives-I: The permanent-magnet synchronous motor drive [J]. IEEE Transactions on Industry Applications, 1989, 25(2): 265-273.

[3] Pillay P, Krishnan R. Modeling of permanent magnet motor drives [J]. IEEE Transactions on Industrial Electronics, 1988, 35(4): 537-541.

[4] 唐任远 (Tang Renyuan).现代永磁电机理论设计(Modern permanent magnet machines theory and design)[M]. 北京:机械工业出版社 (Beijing: China Machine Press), 1999.

[5] Boussak M, Jarray K. A high-performance sensorless indirect stator flux orientation control of induction motor drive [J]. IEEE Transactions on Industrial Electronics, 2006, 53(1):41-49.

[6] Morimoto S, Sanada M, Takeda Y. Wide-speed operation of interior permanent magnet synchronous motors with high-performance current regulator [J]. IEEE Transactions on Industry Applications, 1994, 30(4): 920-926.

Design strategy of control parameters for permanent magnet synchronous motor

QIU Teng-fei1,2, WEN Xu-hui1,3,4, ZHAO Feng1,3,4, WANG Yong-xing1,3,4

(1. Institute of Electrical Engineering, Chinese Academy of Sciences， Beijing 100190， China;2. University of Chinese Academy of Sciences， Beijing 100049， China;3. Key Laboratory of Power Electronics and Electric Drive, Beijing 100190， China;4. Beijing Engineering Laboratory of Electrical Drive System & Power Electronic Device Packaging Technology, Beijing 100190，China)

Field oriented control (FOC) has become the most widely used method of permanent magnet synchronous motor because of its good decoupling, small torque ripple and easy realization. Current loop parameter design is the key of field oriented control. In this paper, the relationship between the control parameters and the performance of current control is deduced with the method of transfer function analysis. The optimal selection principle of control parameters is given.

permanent magnet synchronous motor (PMSM); PI parameter design; vector control

2015-12-07

邱腾飞 (1990-), 男, 山东籍, 博士研究生, 研究方向为电力电子与电力传动； 温旭辉 (1963-)， 女， 四川籍， 研究员， 博士生导师， 主要从事电机驱动与电力电子技术研究。

TM341

A

1003-3076(2016)06-0060-07