基于概率潮流的主动配电网储能配置与控制设计

肖园园， 杨艺云， 高立克， 吴丽芳， 俞小勇

(广西电网有限责任公司电力科学研究院， 广西 南宁 530023)

基于概率潮流的主动配电网储能配置与控制设计

肖园园， 杨艺云， 高立克， 吴丽芳， 俞小勇

(广西电网有限责任公司电力科学研究院， 广西 南宁 530023)

分布式电源的高间歇性使电网承受较大的功率波动，而结合储能技术的主动配电网能充分发挥分布式电源与主动负荷间协调效益，对分布式电源的稳定运行起到重要作用。本文基于Monte Carlo概率理论研究分布式电源接入后的概率潮流，通过概率统计方法来处理系统随机运行状态，并据此对储能系统进行最优容量配置。以电池储能系统为例，根据其出力特征与约束条件，设计一套含多种状态模式的控制策略。在DIgSILENT PowerFactory中验证该配置与控制方案能有效抑制逆向潮流、提高电压质量和降低网损，并实现削峰填谷。

概率潮流； 主动配电网； 电池储能系统； 容量配置； 运行控制策略

1 引言

高渗透率的分布式电源(Distributed Generation, DG)发展为传统配电网带来了功率短时剧烈波动、双向潮流难以管控等问题，主动配电网(Active Distribution Network, ADN)可以通过对多种分布式能源与主动负荷的协调控制，完善分布式能源接入后的潮流管理，实现配电层级的功率平衡[1]。储能系统(Energy Storage System, ESS)因同时具备充放电能力，能在配电层级平抑分布式电源出力波动，是实现主动配电网灵活功率主动调节的重要手段之一[2,3]。同时，储能系统兼具削峰填谷、 消纳逆向潮流等性能，在提高经济性、改善电能质量、缓解配电变压器过载压力等方面都能发挥积极作用。

将储能系统应用到配电网的功率主动调节能力，会受网络潮流的约束与分布式电源出力不确定性的影响；并且储能系统的充放电状态又会影响配电网潮流，其迅速的充放电响应将使配电网的动态过程更为复杂；此外，目前储能系统造价较高，其容量需结合经济性进行合理配置。因此，对储能系统进行合理的配置与控制，使其能满足主动配电网投资与调节能力的需求，针对这方面的研究很有必要[4-7]。

文献[8]从含风电接入的配电网的安全运行角度分析了储能系统的功能与容量配置，未考虑ESS充放电特征；文献[9]针对储能装置的特点，设计工作状态及控制策略，保证含分布式电源接入的系统内部功率；文献[10]从经济性角度分析储能系统容量配置与变电站扩容的协调规划，得出ESS能提高系统总体效益的结论；文献[11-13]分别采用概率潮流和动态规划方法配置ESS，研究分布式能源接入后对配网削峰填谷作用，但仅涉及ESS的控制约束条件。

主动配电网中的储能容量配置是对配电变压器容量的积极补充。本文针对主动配电网中分布式电源的出力不确定性，并基于概率潮流的计算结果，优化ESS容量配置；且根据选用的电池储能系统(BESS)的出力特征与约束条件，结合配电网运行参数，设定强制、协调与空闲三种受控状态对BESS充放电模式进行配置研究。利用DIgSILENT PowerFactory仿真工具，有效验证本文所提的配置与控制方案能提高电能质量及削峰填谷。

2 概率潮流与概率分布模型

2.1 主动配电网中的概率潮流计算

概率潮流方法是采用概率模型来表示主动配电网中的间歇性DG与负荷，以解决DG出力不确定性而导致的运行状态表述问题。即通过概率统计方法来处理系统随机运行状态，为主动配电网的安全调度运行提供更全面的决策信息。

本文采用Monte Carlo原理的概率潮流算法，对DG类型和出力特征进行分类和取样，计及不同类型的负荷，将样本随机组合并进行潮流计算，从潮流解中统计出潮流分布情况。

2.2 光伏发电系统概率模型

光伏发电系统的发电功率主要由光照强度决定且受多种因素制约，但因地面光照强度的随机性，光伏发电系统的发电功率也是随机的，发电功率存在较大波动，但整体上仍有规律可循。

理想情况下一日内地面太阳光照射强度可满足如下关系：

(1)

式中，Emax为一天最大光照强度；T为太阳光光照时间；t0为一天开始日照时间。

实际情况下，太阳光透过大气层照射到地面，会受到随机地表空气阻碍的影响。文献[14]提出，在一定的时间范围内，地面实际光照强度可看作是Beta分布，其概率密度如下：

(2)

式中，e和emax分别为该时段内实际和最大光照强度；α、β均为Beta分布参数。光伏电池将光能转换为电能，则该组光伏电池输出功率为：

P=ηPVeS

(3)

式中，ηPV为光伏电池转换效率；S为光伏电池有效辐照面积。

根据式(2)和式(3)可知，光伏电池的输出功率也呈Beta分布，其概率密度为：

(4)

式中，Pmax=SηPVemax为光伏电池最大功率。

2.3 风力发电系统概率模型

风力发电系统输出功率的大小直接取决于随机风速的变化，本文采用威布尔分布建立风速的概率模型，其概率密度函数为：

(5)

式中，v为风速；k、c分别为威布尔分布的形状参数与尺度参数。

目前，在配电网中广泛使用的变速恒频风电机组的发电功率与风速的函数关系为：

(6)

式中，k1=Pr/(vr-vi)；k2=-k1vi；vi、vr、vo分别为风力发电机切入风速、额定风速、切出风速；Pr为额定功率。

结合式(5)和式(6)可建立风力发电系统概率模型，当风速v落在(vi,vr)区间时，风力发电系统的输出功率与风速v近似威布尔分布。

2.4 负荷概率模型

配电网负荷变化与所在地区的经济活动密切相关，具有一定的周期性和规律性。图1为某地区典型民用负荷与商业负荷变化曲线[15]。

图1 典型居民/商业日负荷曲线Fig.1 Load curves for residential and commercial use in typical day

负荷曲线只反映负荷总的变化趋势，而实际电力负荷是由人的社会活动决定的，因此也具有随机性和独立性。本文用正态分布表示电力负荷波动的特性，其负荷概率模型为：

PL(t)=P1(t)+ΔP(t)

(7)

式中，PL(t)表示负荷在t时刻的有功功率；P1(t)为t时刻基础日负荷值；ΔP(t)为t时间负荷随机波动值。在主动配电网计算概率潮流时，可使用预测算法将负荷预测值作为负荷概率模型中的基础值使用。

3 电池储能系统特性

3.1 储能系统的设置与性能

与抽水蓄能电站、超级电容器、飞轮等储能装置相比，电池储能系统(如铁锂电池、钠硫电池、氧化还原液流电池等)采用新型蓄电池技术，对地理条件和体积的限制小，能量比更高，响应迅速，且商业化程度高[16]。因此本文选择电池储能系统作为储能研究对象。BESS一般由电池模块、变流器、滤波装置及并网变压器组成，并配备一套电池管理系统。以辐射状配电网络为例的主动配电网中，分布式电源与BESS的典型接入位置如图2所示。

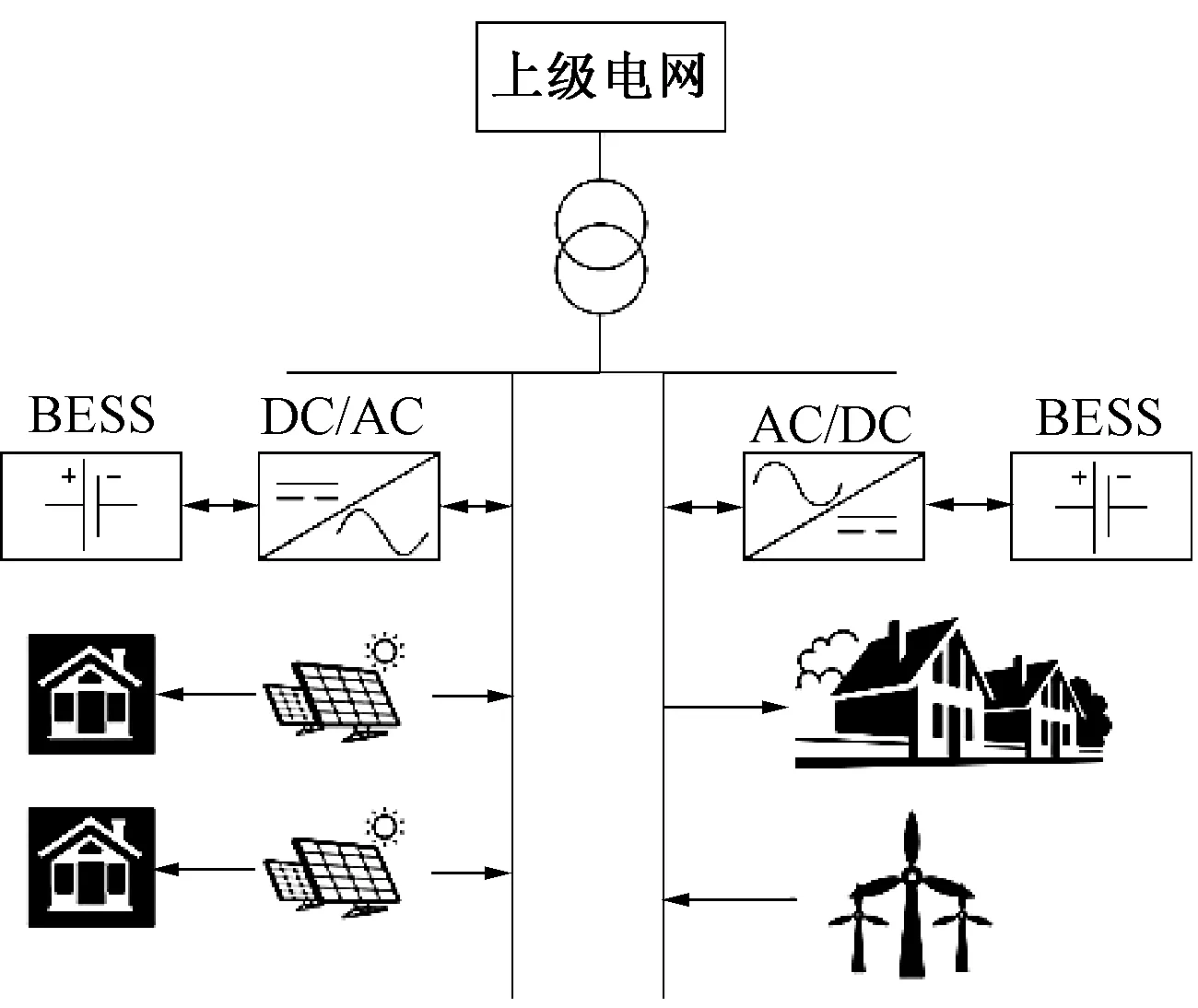
图2 ADN中BESS典型接入位置Fig.2 Typical integration position for BESS in ADN

其中，BESS通常接于配电网变电站低压二次侧，共包含充电、放电与空闲三种工作模式，在控制策略中设置调用情景。光伏、风电等多种分布式电源可以根据出力范围灵活选择接入位置。

3.2 放电模式

(1)变量函数

工作在削峰放电模式下的BESS将维持额定功率范围内的恒定功率输出[17]，放电功率由配变和DG的总功率与目标值的差额决定[18]。

理论上BESS在给定时刻t的视在功率SD(t)(kV·A)需达到：

(8)

式中，PL(t)、QL(t)分别表示负荷在t时刻的有功和无功功率；PT(t)、QT(t)分别表示配电变压器在t时刻的有功和无功功率。

将式(8)求导，得到：

(9)

式中，SL(t)、cosφ分别表示负荷在t时刻的视在功率和功率因数；ST(t)、cosθ分别表示配电变压器在t时刻的视在功率和功率因数。

式(9)左侧的导数值为零，可以得出：

(10)

式(10)表明配变功率因数需与负载相同。工作于这种控制状态下的BESS放电发出的有功功率PD(t)与无功功率QD(t)表示为：

(11)

(2)约束条件

实际工作中的BESS也会受到安装配置的额定功率与额定容量等条件约束，因此，实际能发出的有功功率PD,op(t)和无功功率QD,op(t)为：

(12)

式中，SB,rated表示BESS的视在功率(kV·A)；ES，min表示BESS存储电量下限；Δt表示单个时段的持续时间，E(t-1)与E(t)分别表示t时刻前后一时间段的储能电量(kW·h)；η表示BESS的充放电效率，因为实际运行的电池在充放电过程中总会有一定损耗。E(t-1)与E(t)的关系表示为：

(13)

3.3 充电模式

BESS的充电行为一般发生在光伏等DG产能较大、负荷水平处于低谷状态等电能盈余的时刻，不仅可以补充消耗的电能，也可以实现对逆向潮流的吸收。充电状态下的无功功率为零。Δt时段内的充电功率表示为：

PC(t)=max[-λST,rated-PL(t),0]

(14)

式中，λ表示允许的逆向潮流比例参数，可以在控制策略中设定；ST,rated为额定功率。实际充电时，需考虑额定功率与电量的约束：

(15)

式中，PC,op(t)为实际BESS的实际充电功率；EB,rated为额定电量。

4 储能系统配置与控制设计

4.1 BESS配置原则

BESS容量配置是为了获取满足配功率控制目标要求的最小补偿容量，确定所需的最大充放电功率作为其额定功率，保证BESS连续稳定运行的功率输出。

为满足功率控制目标需求，首先应确保BESS的充放电功率足够维持功率平衡、抑制功率波动，且尽量减小初始投资、保证经济性。即应在运行效果较优的情况下尽量减少BESS配置的放电功率。本文提出的BESS配置原则建立在第2节含分布式电源的Monte Carlo概率潮流基础上，根据BESS工作模式，将BESS的受控状态分为：

(1) 强制状态。包含强制充电和强制放电。前者定义发生逆向潮流概率较大、配变二次侧过载概率较小的系统状态，如午间光伏出力高峰时段；后者定义发生逆向潮流概率较小、配变二次侧过载概率较大的系统状态，如晚间用电高峰时段。

(2) 协调状态：发生逆向潮流越限与配变二次侧过载的概率均较小，如深夜时段，根据系统需求，BESS进行充放电切换。

(3) 空闲状态：除状态(1)和状态(2)之外。

根据主动配电网的控制需求，取一合理的置信水平如98%，即可根据BESS未接入时某自然日下的概率潮流计算结果得到其配置方案。在BESS配置阶段考虑功率与电量的理论值，以式(16)取置信水平内的最大值作为BESS配置，通过计算每日总充放电电量和BESS工作在充放电的时段数，绘制其概率累积曲线。实际配置时，需考虑到模块化生产的BESS容量值的离散性。

(16)

式中，SC,max、SD,max分别表示最大充、放电视在功率；EB,Rev表示剩余电量；EC,max、ED,max分别表示最大充、放电量；EC,min表示最小充电量。

4.2 控制设计

配置与控制流程如图3所示。在根据概率潮流配置BESS后，以实际安装的BESS容量作为运行控制的约束条件，并设定如下三种状态：

(1)强制状态。当逆向潮流比例达到参数λ时，BESS切换至强制充电状态，充电功率与剩余电量如式(15)所表示；当进入用电高峰、变压器过载概率达到置信水平时，切换至强制放电状态，充电功率与剩余电量如式(12)和式(13)所表示。

(2)协调状态。指定一个系统建议的协调状态切换容量Ectr。当BESS电量低于Ectr时进入协调充电状态，此时有功功率PC,op(t)如式(17)所示，直至电量充满或判断其进入其他状态。

(17)

当BESS电量高于Ectr时，以有功功率PD,op(t)(如式(18)所示)为其放电，直至电量至设定的最低值或判断其进入其他状态。

(18)

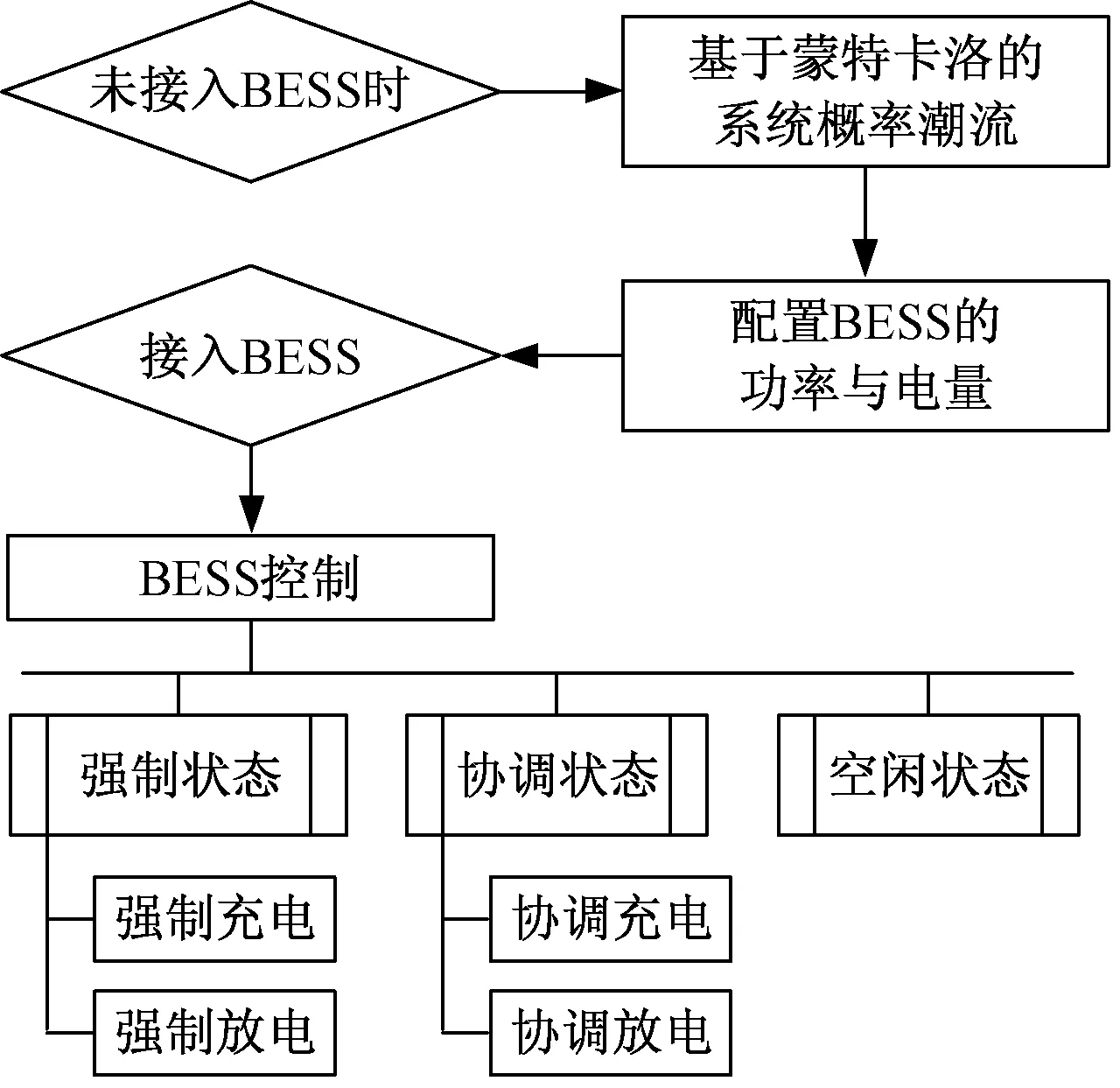
图3 BESS配置与控制流程Fig.3 Configuration and control flow for BESS

5 算例分析

5.1 算例说明

本文在CIGRE-C6.04.02工作组给出的模型系统上进行仿真，该系统额定基准电压为20kV，其他数据参照文献[18]所述，其网络结构如图4所示。该测试系统中的联络开关S1、S2、S3处于打开状态，不考虑系统网络拓扑结构重构的情况，在节点8处接入BESS，最大充放电功率为2MW。使用基于Monte Carlo抽样的概率潮流计算方法对测试系统进行仿真验证。

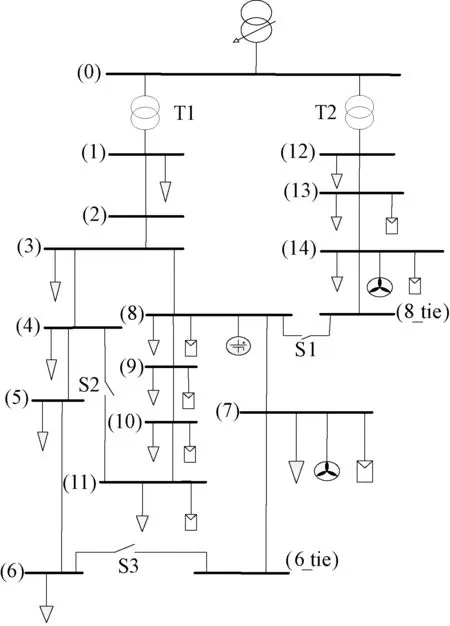
图4 CIGRE工作组系统接线图Fig.4 CIGRE-defined system connection diagram

根据本文采用的BESS配置流程，分3种方案对该测试系统进行仿真：①方案1，不考虑DG和BESS，只考虑负荷随机波动；②方案2，考虑DG和负荷的随机波动，未配置BESS；③方案3，考虑DG和负荷随机波动，并按第4节所述配置和控制BESS。

该测试系统中，风力发电系统风机型号为GW70/1500，单个风机额定功率为1500kW，6台机组并联运行，切入风速3m/s，额定风速12m/s，切出风速25m/s；光伏发电系统太阳能电池组件型号为CHN96M 270W，最大功率电流5.45A，最大功率电压49.50V，光电转换效率16.09%，光伏发电系统最大发电功率0.95MW。本文采用的气象数据以国家气象局网站发布的广西某市2014年历史天气数据为基础进行模拟。

5.2 仿真结果

图5 BESS对逆向潮流的影响Fig.5 Influence of BESS for reverse flow

首先比较方案2和方案3在DG发电功率最大时，BESS对配电网发生逆向潮流的影响。选取2条典型线路line1-2和line3-8，t=13:00时，DG出力最大，发生逆向潮流的概率如图5所示。

未配置BESS时，当DG出力达到最大，line3-8和line1-2必然会发生反向潮流，尽管由于上游负荷的存在，吸收了部分line3-8的反向功率，line1-2的反向潮流变小，但是由于反向潮流的存在，仍然会对上游变压器T1的保护开关产生作用，影响保护配置的效果。配置BESS后，显著降低了系统发生反向潮流的概率，line1-2在500次抽样结果中未发生反向潮流，BESS对系统安全稳定运行产生积极作用。

BESS在吸收系统反向潮流的同时也可以改善系统电压的波动。风电系统发电时需吸收无功，同时负荷的无功也具波动性，因此，对于含DG的配电网，电能质量是配置BESS时需要考虑的一个重点。三种方案下节点8处的电压波动情况如图6所示。

图6 节点8电压幅值波动曲线Fig.6 Voltage magnitude curves of node 8

从图6可以看出，合理的BESS配置能够改善系统电压幅值的波动，防止发生电压越限，DG与BESS组合使用可以为电力用户提高更好的电力服务。

传统配电网电力峰谷差仅由电力负荷的变化决定，在接入DG后，特别是光伏发电系统，有明显的发电峰值期，当DG的发电容量比较大时，必然会给配电网带来新的峰谷差。图7比较了方案2和方案3节点8处的有功功率潮流。可见由于BESS的存在，节点8处有功潮流波动得到抑制，上游变压器工作在一个相对平稳的负荷水平，整个配电网处于一个比较稳定的状态，这对于配电网降低损耗具有重要意义。

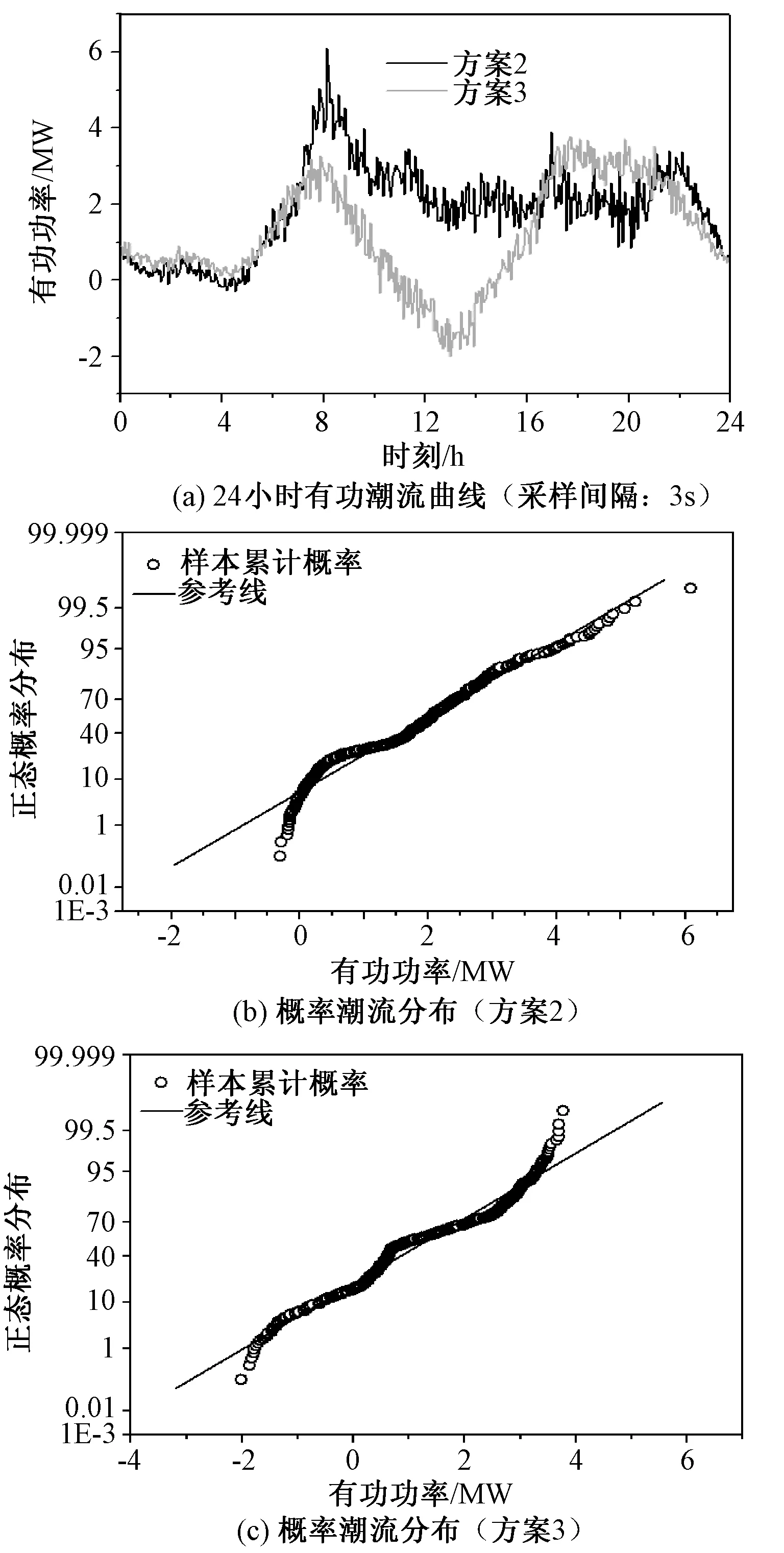
图7 节点8有功潮流曲线与概率分布Fig.7 Power flow curves and its probability distribution of node 8

表1针对三种方案中在一天时间跨度内该测试系统总的网络损耗进行了比较。可以看出，DG接入配电网后降低了电能远距离传输产生的线路损耗，再接入合理配置的BESS后，BESS削峰填谷的作用可以进一步降低网络损耗，有助于配电网的经济运行。

表1 系统网络损耗Tab.1 Power loss of system

5.3 分析与比较

在配电网中安装BESS是解决分布式电源随机波动导致难以并网的有效方法之一。与基于平抑分布式电源功率波动的储能控制设计思路不同，本文提出的基于概率潮流的储能配置与控制设计方法，通过对配电网概率潮流进行计算，根据发生逆向潮流的比例作为储能系统充放电控制主要的判断依据，重点保护上游配电变压器，避免出现功率倒送，防止保护误动作，对储能系统的响应速度与跟踪速度要求不高。仿真结果表明，采用本文提出的控制方法能够有效维持电压稳定，抑制反向潮流，降低网络损耗，对配电网安全运行具有重要意义。

6 结论

本文以基于Monte Carlo抽样的概率潮流方法，计算含常见DG类型与容量的主动配电网概率潮流，并据此结果对储能系统进行合理配置。根据BESS出力特性与约束条件，拟定包含强制充放电、协调充放电和空闲状态的控制方案，并预设判断依据和控制策略。通过在DIgSILENT PowerFactory中建模仿真，验证本文提出的储能系统配置与控制方法可以抑制逆向潮流，提高电压质量，平抑峰谷，降低系统网损。

[1] 范明天, 张祖平, 苏傲雪, 等 (Fan Mingtian, Zhang Zuping, Su Aoxue, et al.). 主动配电系统可行技术的研究 (Enabling technologies for active distribution systems) [J]. 中国电机工程学报 (Proceedings of the CSEE), 2013,33 (22): 12-18, 5.

[2] 余昆, 曹一家, 陈星莺, 等 (Yu Kun, Cao Yijia, Chen Xingying, et al.). 含分布式电源的地区电网动态概率潮流计算 (Dynamic probability power flow of district grid containing distributed generation) [J]. 中国电机工程学报 (Proceedings of the CSEE), 2011, 31(1): 20-25.

[3] 刘东, 陈云辉, 黄玉辉, 等 (Liu Dong, Chen Yunhui, Huang Yuhui, et al.). 主动配电网的分层能量管理与协调控制(Hierarchical energy management and coordination control of active distribution network) [J]. 中国电机工程学报(Proceedings of the CSEE), 2014, 34(31): 5500-5506.

[4] 王成山, 于波, 肖峻, 等 (Wang Chengshan, Yu Bo, Xiao Jun, et al.). 平滑微电网联络线功率波动的储能系统容量优化方法 (An energy storage system capacity optimization method for micro grid tie-line power flow stabilization) [J]. 电力系统自动化 (Automation of Electric Power Systems), 2013, 37(3):12-17.

[5] 尤毅, 刘东, 钟清, 等 (You Yi, Liu Dong, Zhong Qing, et al.).主动配电网储能系统的多目标优化配置(Multi-objective optimal placement of energy storage systems in an active distribution network) [J]. 电力系统自动化(Automation of Electric Power Systems), 2014, 38(18): 46-52.

[6] 丁明, 徐宁舟, 毕锐 (Ding Ming, Xu Ningzhou, Bi Rui). 负荷侧新型电池储能电站动态功能的研究(Dynamic model of new-type battery energy storage system at demand side) [J]. 电力自动化设备 (Electrical Power Automation Equipment), 2011, 31(5): 1-7.

[7] 刘琳，陶顺，肖湘宁，等(Liu Lin，Tao Shun，Xiao Xiangning，et al.). 分布式发电及其对配电网网损的影响分析 (Distributed generation and its impact on network loss of power system) [J]. 电工电能新技术 (Advanced Technology of Electrical Engineering and Energy), 2012, 31(3): 16-19.

[8] Atwa Y M, El-Saadany E F. Optimal allocation of ESS in distribution systems with a high penetration of wind energy [J]. IEEE Transactions on Power Systems, 2010, 25(4): 1815-1822.

[9] 董博, 李永东, 郑治雪 (Dong Bo, Li Yongdong, Zheng Zhixue). 分布式新能源发电中储能系统能量管理(Application of expert system and visualization in grid maintenance scheduling) [J].电工电能新技术 (Advanced Technology of Electrical Engineering and Energy), 2012, 31(1): 22-25, 96.

[10] 李振文, 颜伟, 刘伟良, 等 (Li Zhenwen, Yan Wei, Liu Weiliang, et al.). 变电站扩容和电池储能系统容量配置的协调规划方法 (Coordinated planning of substation expansion and BESS sizing) [J]. 电力系统保护与控制(Power System Protection and Control), 2013, 41(15): 89-96.

[11] Hans B, José D. A probabilistic method for energy storage sizing based on wind power forecast uncertainty [J]. IEEE Transactions on Power Systems, 2011, 26(3):1651-1658.

[12] P Pinson, G Papaefthymiou, B Klockl, et al. Dynamic sizing of energy storage for hedging wind power forecast uncertainty [A]. IEEE Power & Energy Society General Meeting [C]. 2009. 1-8.

[13] 鲍冠南, 陆超, 袁志昌, 等 (Bao Guannan, Lu Chao, Yuan Zhichang, et al.). 基于动态规划的电池储能系统削峰填谷实时优化 (Load shift real-time optimization strategy of battery energy storage system based on dynamic programming) [J].电力系统自动化(Automation of Electric Power Systems), 2012, 36(12): 11-16.

[14] Karaki S H, Chedid R B. Probabilistic performance assessment of autonomous solar-wind energy conversion systems [J]. IEEE Transactions on Energy Conversion， 1999, 14(3): 766-772.

[15] Kadurek P, Kling W L, Ribeiro P F, et al. Electricity demand characterization for analyzing residential LV distribution networks [A]. 2013 IEEE Grenoble PowerTech[C]. 2013. 1-5.

[16] 丁明, 张颖媛, 茆美琴, 等 (Ding Ming, Zhang Yingyuan, Mao Meiqin, et al.). 包含钠硫电池储能的微网系统经济运行优化 (Economic operation optimization for microgrids including Na/S battery storage) [J]. 中国电机工程学报 (Proceedings of the CSEE), 2011, 31(4): 7-14.

[17] 钟宇峰 (Zhong Yufeng). 微电网中电池储能系统的动态优化调度及可靠性建模问题研究 (Research on operation optimization and reliability modeling of battery energy storage system in micro grid) [D]. 杭州: 浙江大学 (Hangzhou: Zhejiang University), 2014.

[18] Nikolaos P. Voltage control in MV distribution networks with a large share of distributed renewable generation [D]. Delft: Delft University of Technology, 2013.

tanφ(t)=tanθ(t)

BESS configuration and control design for ADN based on probabilistic load flow

XIAO Yuan-yuan， YANG Yi-yun， GAO Li-ke， WU Li-fang， YU Xiao-yong

(Guangxi Power Grid Electric Power Research Insititute, Nanning 530023, China)

With the high-penetration of the intermittent distributed generation (DG), the grid will endure great power fluctuation. However, high efficiency of DGs and active load can be achieved by the active distribution network (ADN). The configuration and operation schedule of the battery energy storage system (BESS) will help the ADN staying in a relatively steady state. Probabilistic power flow, comparing with the deterministic power flow, can provide more information about the possible future conditions of the power system. The characters of the key point nodes are analyzed, and the possible ranges are identified. After the optimal configuration of BESS based on the Monte Carlo probabilistic load flow, a control schedule with multi-modes is designed by the characters of the system. The model is simulated in PowerFactory and proved to be a good solution to help restraining reverse power flow, improving voltage quality and decreasing network loss, also with load shifting ability.

probabilistic load flow; active distribution network; battery energy storage system; capacity configuration; operational control schedule

2015-07-28

肖园园(1987-)， 女， 湖南籍， 工程师， 硕士研究生， 主要研究方向为电力系统运行分析与控制、 新能源应用技术等。 杨艺云(1975-)， 男， 广西籍， 高级工程师， 主要研究方向为新能源应用技术、 智能电网及需求侧新技术。

TM911；TN710

A

1003-3076(2016)06-0074-07