基于QoS参数的电力线信道状态映射方法

胡正伟，谢荣圆，谢志远

（华北电力大学 电子与通信工程系，河北 保定 071003）

0 引言

电力线通信 PLC（Power Line Communication）技术是智能电网和室内宽带接入所采用的重要的通信方式之一。经过国内外相关研究机构和学者的研究，电力线通信技术取得了快速的发展［1-3］。但由于电力线信道受到噪声干扰、阻抗匹配、信号衰减、负载多样性且具有时变性等因素的影响，再加上电力线通信网络结构复杂，导致了电力线通信可靠性问题一直未能得到很好的解决，在一定程度上制约了电力线通信技术的应用。此外，随着智能电网技术的发展，配电网通信业务大量涌入，对数据业务的可靠性和有效性等指标提出了更高的要求。因此，研究基于电力线通信技术实现数据业务的有效传输具有重要的实用价值。

数据传输的可靠性依赖于信道状态，目前研究者针对电力线信道特性的研究主要集中在信道的衰减、阻抗等物理特性［4-11］及噪声［12-16］等，这些物理参数虽然能反映电力线信道的状态，但无法与基于服务质量QoS（Quality of Service）参数的业务传输指标需求之间建立直观的联系。

为了解决上述物理参数表示信道状态存在的问题，本文提出了基于QoS参数的电力线信道状态映射方法。本文方法具有以下优点：可以将映射得到的电力线信道的QoS参数与业务的QoS参数进行比较，从而验证当前电力线信道状态是否具备相关业务的传输能力；中继技术已被广泛认为可有效提高电力线通信的可靠性及通信距离，本文方法可以有效支持以QoS参数为约束条件的路由搜索算法，为在网络层开展电力线通信的组网研究提供了一定的参考。

本文根据已有文献对电力线信道的物理参数的研究，对信道的误码率、信道容量、时延及时延抖动等QoS参数进行了分析，确定了各QoS参数的取值或概率分布。在此基础上，通过合理地设置工作频带、衰减因子、背景噪声、发送功率等条件，基于OPNET建立了包含误码率、信道容量、时延及时延抖动4个QoS参数的电力线信道状态模型，并进行了相关仿真分析，验证了本文方法的可行性和有效性。

1 电力线信道状态的物理特性分析

1.1 衰减特性分析

电力线信道的信号衰减由耦合衰减和线路衰减两部分组成，理论上可以将耦合器内阻做得相当小，因此可认为电力线信道的衰减主要取决于线路衰减。

假设发送节点的功率为PT（单位：dB），接收节点的功率为 PR（单位：dB），距离衰减因子为 PL（单位：dB／km）。接收功率PR与传输距离d的关系可表示为：

式（1）中的各功率转换至以W为单位时有：

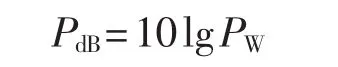
其中，PdB和PW分别为以dB和W为单位的功率。

若使用功率单位W，则接收功率和发送功率的关系为：

1.2 幅度衰落分析

本文引用文献［17］给出的幅度衰落模型。

频率选择性衰落和信号的相干带宽有关，如果相干带宽大于信号带宽，则信道呈现频率平坦衰落，否则呈现选择性衰落。当电力线网络拓扑分支数量较少时，有较大的相干带宽［18-19］，此时可假设信号带宽小于相干带宽，即假设信道为平坦衰落信道。

文献［17］提出，如果发送节点到目的节点有N跳，其衰落幅度为 h1、h2、…、hN，当每跳的通信频率不同时，每跳幅度衰落都是独立同分布的，且服从lognormal分布，第 i（i=1，2，…，N）跳的衰落幅度 hi满足的概率密度函数表达式为：

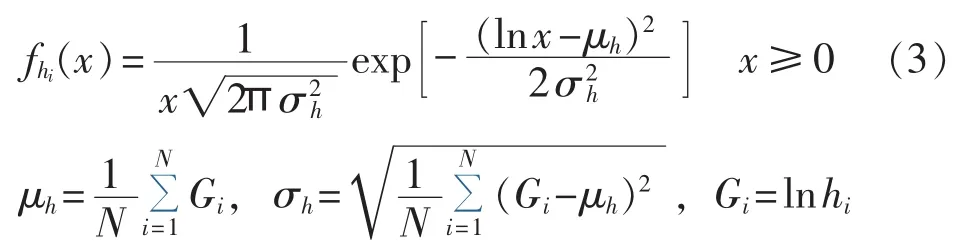
hi的 m 阶矩表示为 E=exp当=1 时，有 μh=-

因为每跳幅度衰落之间满足独立同分布，所以当发送节点和目的节点的跳数N=1时，式（3）可简化为：

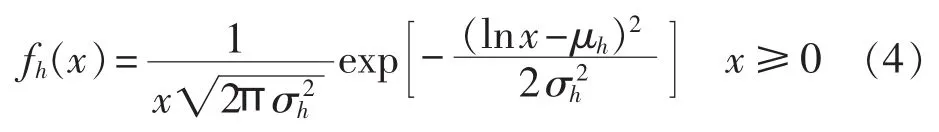
1.3 噪声分析

电力线信道噪声主要由背景噪声和脉冲噪声造成，且脉冲噪声和背景噪声随时间变化是相互独立的［20］。为了研究噪声在电力线通信系统中的影响，本文参考文献［21］给出的包含背景噪声和Bernoulli-Gaussian脉冲噪声的统计模型。假设N跳节点中第i跳的总噪声采样值为zi，则有：

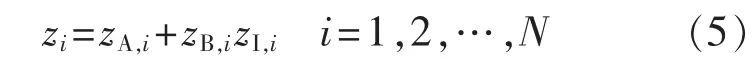
其中，zA，i和 zI，i分别为具有均值为 0 的背景噪声（加性高斯白噪声（AWGN））采样值和脉冲冲击噪声采样值，方差分别为为具有参数 p 的Bernoulli随机序列，且 p 与 zA，i和zI，i相互独立。

每跳的噪声采样值是独立同分布的随机变量，第i跳噪声采样值的概率密度函数可表示为：

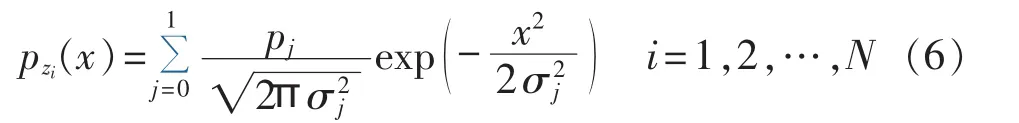
其中

如果每个节点传输信号的频率不同，并且节点间满足一定距离，则可以认为各跳噪声之间满足独立同分布。假设N0为整个链路的平均噪声功率，N0，i为第i跳的噪声平均功率，则有：

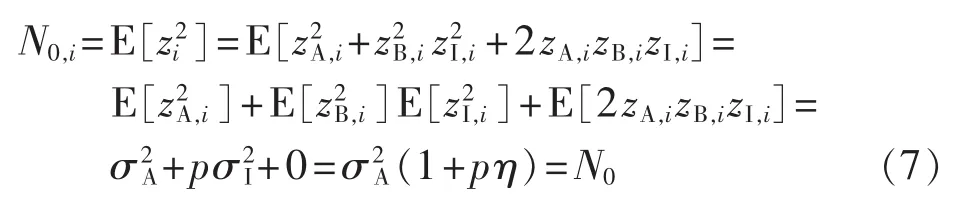
其中式（7）的推导采用 Bernoulli随机分布特性，即 E（X2）=02×（1-p）+12×p=p。

由式（7）可知，任意跳的噪声平均功率与源节点和目的节点间的跳数无关，当源节点到目的节点为单跳时的噪声平均功率也为N0。

1.4 信噪比分析

假设第i跳的瞬时信噪比为γi，则：

其中，PR，i为第i跳接收节点的功率。

当发送节点到目的节点为单跳时，式（8）可简写为：

由文献［17］可知，衰落幅度hi服从 log-normal分布，则信噪比γi服从log-normal分布：

单跳时，信噪比的概率分布函数表达式为：

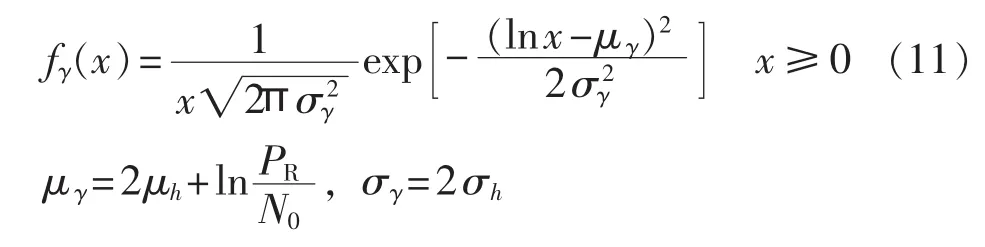
2 基于QoS参数的电力线信道状态模型

QoS是衡量一个通信网络业务传输能力优劣的标准之一。QoS指标包括：时延、时延抖动、丢包率、带宽、吞吐率等。与专用通信网络相比，电力线信道的时变特性更增加了保证业务QoS的难度。

图1为本文提出的电力线通信信道状态的QoS参数模型示意图，该模型包含误码率、信道容量、时延和时延抖动4个QoS参数。

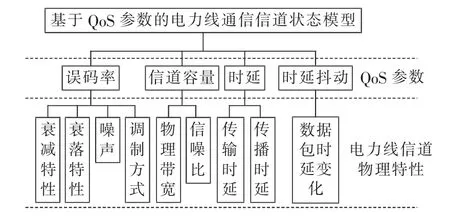
图1 基于QoS参数的电力线信道状态模型Fig.1 PLC channel status model based on QoS parameters

2.1 误码率

误码率是衡量数据在规定时间内数据传输精确性的指标。决定误码率的因素包括信道的衰减特性、衰落特性、噪声以及调制解调方式。本文将电力线通信信道的衰减、幅度衰落、噪声干扰、调制解调方式等因素通过数学推导等效为电力线通信信道的误码率。

根据1.4节所得瞬时信噪比的概率密度函数可得到不同调制方式下的误码率，当以二进制进行编码时，误比特率Pe即为误码率［22］。当存在多跳情况时，Pi，e表示第 i跳的误码率。

a.当调制方式为移频键控（FSK），且采用相干解调方式时，有：

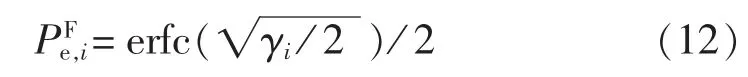
根据文献［23］给出的误差函数的近似表达式：

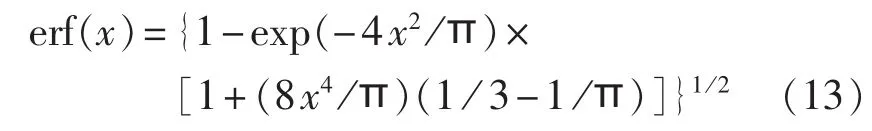
可知互补误差函数 erfc（x）=1-erf（x）。

将近似表达式和互补误差函数代入式（12），得调制方式为FSK时误码率的近似表达式为：

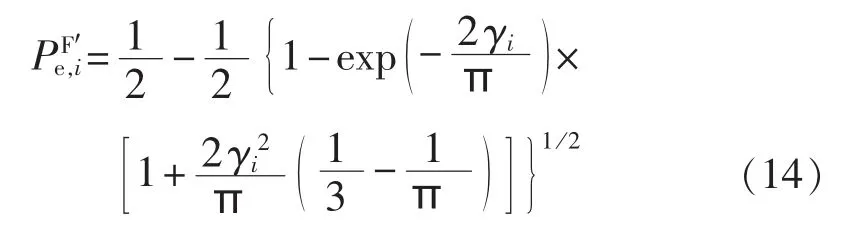
b.当调制方式为二进制相移键控（BPSK）时，误码率的表达式和近似表达式分别如式（15）、（16）所示。

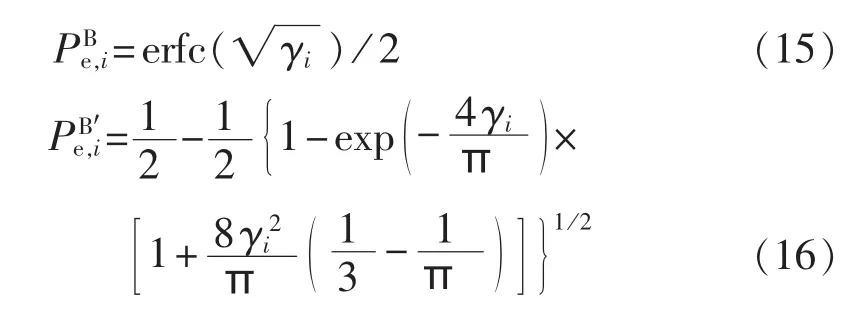
c.当调制方式为正交相移键控（QPSK）时，误码率的表达式和近似表达式分别如式（17）、（18）所示。

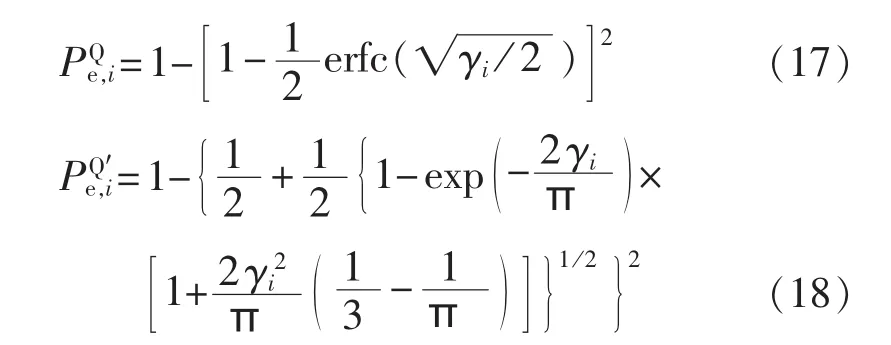
2.2 信道容量

信道容量即理论最大传输速率。单跳时，根据香农公式，得信道容量C=Bln（1+γ），其中B为物理带宽。因此可根据信噪比γ的概率分布函数式（11）求出信道容量C的概率分布特性。

2.3 时延

通信网络的数据包时延主要包括传输时延、传播时延和队列时延3个部分。传输时延与包长度和传输速率有关；传播时延与介质和传输距离有关；队列时延与队列类型、容量、网络状态有关，在反映信道的物理状态时，可不考虑队列时延。

定义τ（t）、τT（t）、τP（t）分别为数据包总时延、传输时延和传播时延，则有：

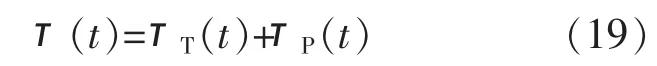
（1）传输时延τT（t）。

传输时延由包长度和信道传输速率决定。定义Spacket为包长度，C（t）为传输速率，则发送时延τT（t）=电力线信道特性决定了传输速率C（t）具有时变性，在Spacket一定的情况下，发送时延完全依赖于传输速率 C（t）。单跳时，若 C（t）取香农定理的极限值，即 C（t）=Bln（1+γ），则τT（t）=

（2）传播时延τP（t）。

传播时延取决于电信号的传播速率与传输距离。电信号的传播速率为：

其中，c0为光速；εr、μr分别为导线的介电常数和磁导率。

传输距离为d时，传播时延可表示为：

2.4 时延抖动

时延抖动即时延的变化，在电力线信道中，介质和通信节点固定，在包长度相等的情况下，时延抖动与传输速率有关。

若定义 Δτ（t）为时延抖动，则 Δτi，i-1（t）=τi（t）-τi-1（t），其中τi（t）和τi-1（t）分别表示第 i个数据包的总时延。

3 仿真模型

为了验证本文所提方法的可行性和有效性，建立了具备特定电力线通信信道状态的P2P电力线通信系统，并分析了相关QoS参数。图2为本文建立的P2P电力线通信系统示意图，系统中包含主节点和从节点2个节点，这2个节点都具备接收和发送功能。

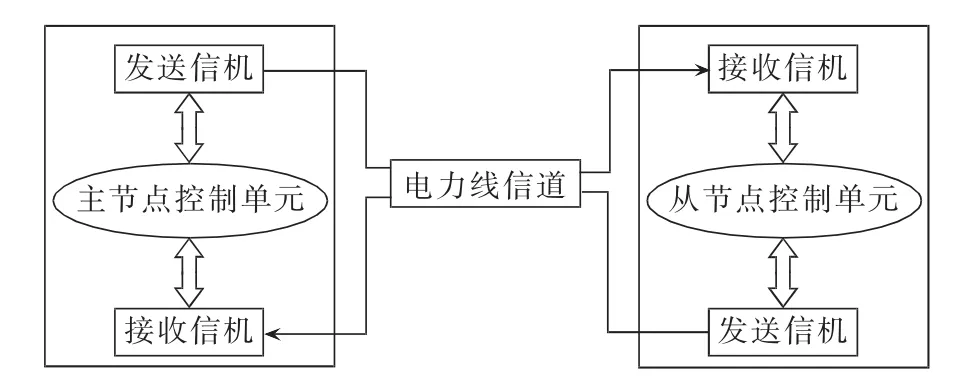
图2 P2P电力线通信系统Fig.2 P2P PLC system

3.1 主节点

数据传输由主节点发起，主节点经电力线信道向从节点发送一个命令数据包，当收到从节点返回的数据包后，主节点开始发送下一个数据包。如果主节点发送一个数据包后，在规定的时间间隔内未收到从节点返回的数据包，则认为本次通信失败，主节点重新发送该传输失败的数据包，直到发送成功后，才开始发送下一个数据包，即采用自动重传机制。

3.2 从节点

在没有收到主节点发送的数据包时，从节点处于空闲状态。当从节点接收到主节点发来的数据包后，立即向主节点返回一个数据包。

3.3 电力线信道

为了模拟实际的电力线信道状态，需要设置合理的相关物理参数。

（1）工作频带。

根据文献［18］，在 30kHz～100MHz带宽室内电力线通信信道中，相干系数为0.9时90%的测试信道的相干带宽的取值范围为［65.5，691.5］kHz，相干带宽的最小值为32.5 kHz。因此本文选择的物理带宽为25 kHz。当实际通信的物理带宽超过25 kHz时，可以将整个频带以25kHz进行划分，采用正交频分复用（OFDM）实现多载波通信。由于OFDM的每个载波频率不同，每个载波的幅度衰落也服从log-normal分布［21］。本文选择的电力线的频率范围为70～95 kHz。

（2）衰减因子。

电力线信道中信号随距离衰减的取值一般在［40，100］dB／km［17，24-25］范围内。 为了验证本文方法在不同衰减因子下的特性，选取距离衰减因子PL，best=40 dB／km 和 PL，worst=100 dB ／km 作为仿真条件。

（3）噪声功率。

为了确定噪声的功率，需要确定3个参数和η。文献［25］给出了计算电力线AWGN的公式：

其中，f为频率。

在频带70～95 kHz范围内的AWGN可以近似计算［25］为：

选择不同的参数p和η，可以表示不同发生概率和不同幅度的脉冲噪声。考虑信道中存在严重的脉冲噪声时，根据文献［17］，参数 p 设置为 3.27×10-3，参数η设置为10。将参数p、η和代入式（7）可求得：N0，best=4.23×10-14W，N0，worst=4.03×10-11W。

（4）信噪比分布函数。

根据文献［17］将参数 σh设置为 0.69，则 μh=

根据式（11）可得：

其中，PR可由式（2）求得，故信噪比γ的分布函数可求得。

（5）其他参数。

在图2中的电力线通信系统模型中，除了需要确定上述电力线信道特性参数外，还需要设置的参数如表1所示。

表1 其他参数设置Table 1 Setting of other parameters

4 仿真验证及结果分析

4.1 衰减与噪声功率条件设置

相干带宽、噪声功率、衰减因子等参数的设置可能会导致仿真结果存在偏差，考虑到电力线信道由于受很多因素的影响而具有一定的不确定性，这些偏差的存在在一定范围内是允许的。

根据第3节的分析，为了对比不同衰减特性和噪声功率对QoS参数的影响，设置了如表2所示的4种衰减参数和噪声功率参数作为仿真条件。分析比较C1与C2、C3与C4的结果可以得到衰减参数对相关QoS参数的影响，分析比较C1与C3、C2与C4的结果可以得到噪声功率对相关QoS参数的影响。

4.2 QoS 参数分析

（1）误码率。

表3为不同仿真条件及不同调制方式下误码率的统计特性。由表3可见，在相同的信道状态下，BPSK的误码率最小，QPSK的误码率最高。C1条件下，采用BPSK、FSK和QPSK调制方式时，90%的电力线信道的误码率分别不超过 8.0×10-15、6.3×10-8和 1.3×10-7。

表3 误码率统计数据Table 3 Statistic data of BER

（2）信道容量。

在仿真条件C1—C4中，上行信道和下行信道设置为相同的状态，因此每个仿真条件的上行信道和下行信道具有相同的信道容量。表4为不同仿真条件下的信道容量的统计特性，图3为信道容量的概率密度。由表4和图3可以发现，较好的信道状态具有较大的信道容量且信道容量的分布范围较小。当业务的QoS指标参数可以用一段时间来衡量时，可以使用与信道容量的平均值进行比较。

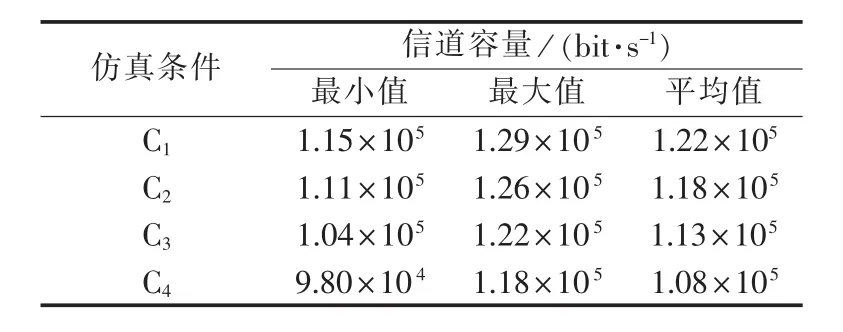
表4 信道容量统计数据Table 4 Statistic data of channel capacity

图3 信道容量的概率密度Fig.3 Probability density of channel capacity

（3）时延。

时延的数值取决于信道容量和数据包的长度。由于主节点和从节点发送的数据包的长度不同，时延的分析需考虑数据包的传输方向。表5为时延参数的统计数据，图4为主节点到从节点和从节点到主节点的时延参数的概率密度。由仿真数据可以发现，信道状态较好时，时延较小并且时延分布的范围较小。

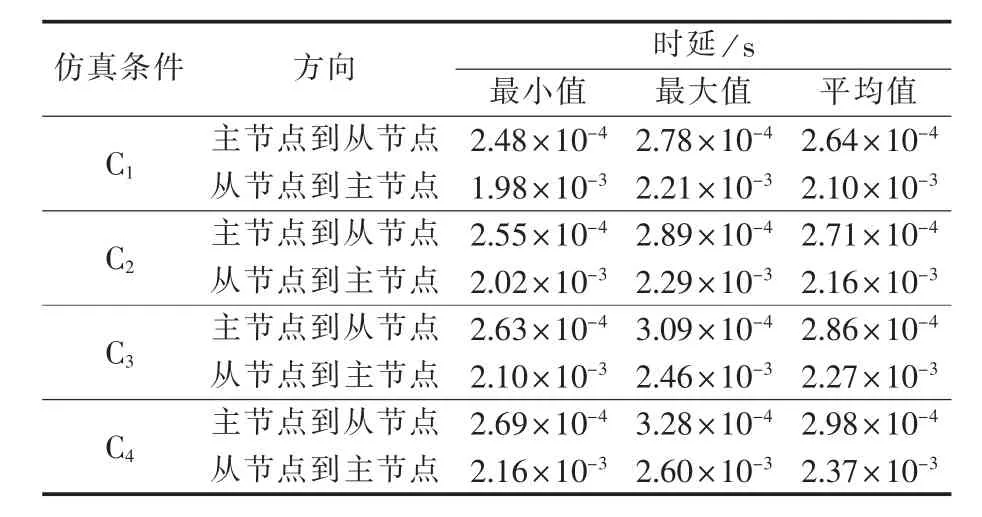
表5 时延统计数据Table 5 Statistic data of time delay

（4）时延抖动。

时延抖动取决于时延，因此同样需考虑数据包的传输方向。表6为时延参数的统计数据，图5为主节点到从节点、从节点到主节点的时延参数的概率密度。由仿真数据可以发现，信道条件较好时，时延抖动的分布范围相对较小。

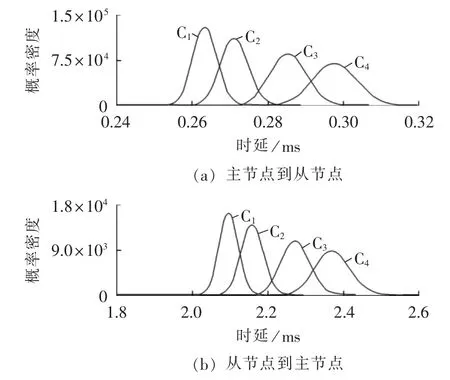
图4 时延的概率密度Fig.4 Probability density of time delay

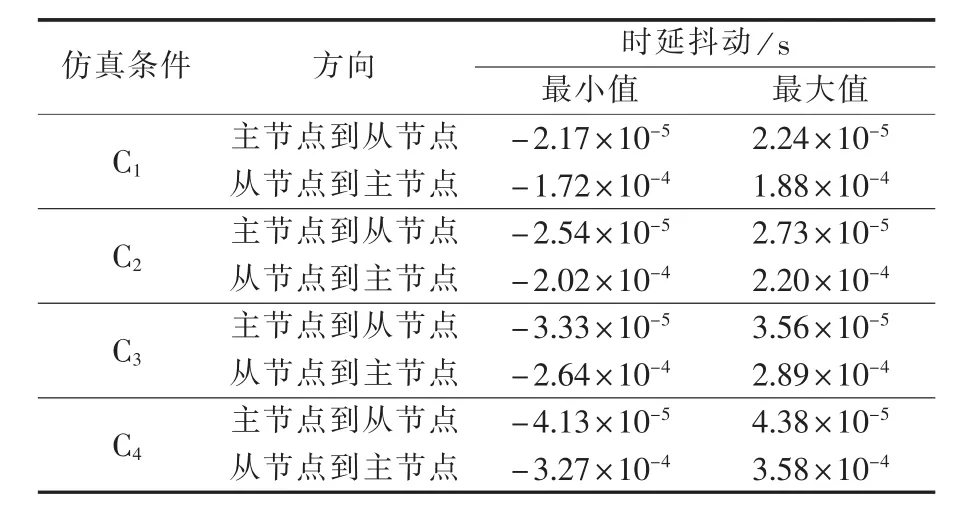
表6 时延抖动统计数据Table 6 Statistic data of delay jitter

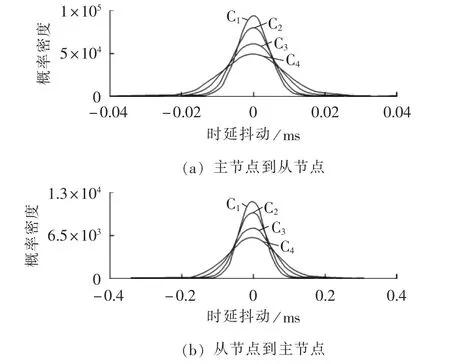
图5 时延的概率密度Fig.5 Probability density of delay jitter

5 结论

通过对具备特定电力线信道状态的P2P电力线通信系统模型的仿真分析，说明了本文所提方法可以将不同电力线信道状态映射为与业务传输相关的QoS参数，验证了本文方法的可行性和有效性。本文为研究基于电力线通信技术现实业务传输提供了一种参考方法，同时，为进一步在网络层研究基于QoS参数的路由选择机制研究提供了技术支持。

此外，本文研究主要存在以下不足：

（1）本文仿真实例中设定的电力线信道状态只是依据已有参考文献的相关统计结果，未能针对实际的电力线通信信道状态进行在线测量；

（2）信道容量只考虑香农定理的上限值，属于理想的情况，实际的信道容量受多种条件的影响，如需考虑信道编码和调制解调方式等；

（3）实际的数据包时延需要考虑队列时延。针对以上不足，需进一步开展的工作包括：

（1）设计电力线通信硬件平台，可以进行电力线信道状态的实时测量，并且能够映射为对应的QoS参数；

（2）在硬件平台的基础上，结合特定的配电网络，研究基于电力线通信实现具备QoS参数需求的业务传输的关键技术。

参考文献：

［1］KHALILK，GAZALETM G，CORLAY P，etal.AnMIMO random channel generator for indoor power-line communication［J］.IEEE Transactions on Power Delivery，2014，29 （4）：1561-1568.

［2］MATANZA J，ALEXANDRES S，RODRÍGUEZ-MORCILLO C.Advanced metering infrastructure performance usingEuropean low-voltage power line communication networks［J］.IET Communications，2014，8（7）：1041-1047.

［3］ARTALE G，CATALIOTTI A，COSENTINO V，et al.Medium voltage smart grid：experimental analysis of secondary substation narrow band power line communication［J］.IEEE Transactions on Instrumentation and Measurement，2013，62（9）：2391-2398.

［4］GUZELGOZ S，CELEBI H B，ARSLAN H.Statistical characterization of the paths in multipath PLC channels［J］.IEEE Transactions on Power Delivery，2011，26（1）：181-187.

［5］GALLIS.A novelapproach to the statisticalmodeling of wireline channels［J］.IEEE Transactions on Communications，2011，59（5）：1332-1345.

［6］BARMADA S，MUSOLINO A，RAUGI M.Innovative model for time-varying power line communication channel response evaluation［J］.IEEE Journal on Selected Areas in Communications，2006，24（7）：1317-1326.

［7］黄文焕，戚佳金，黄南天，等.低压电力线载波通信传输线参数测试与分析［J］. 电力自动化设备，2008，28（4）：41-44.HUANG Wenhuan，QI Jiajin，HUANG Nantian，et al.Experiment and analysis of transmission line parameter for carrier wave communication over low-voltage power line［J］.Electric Power Automation Equipment，2008，28（4）：41-44.

［8］GALLI S，BANWELL T.A novel approach to accurate modeling of the indoor power line channel-part Ⅱ：transfer function and channel properties［J］.IEEE Transactions on Power Delivery，2005，20（3）：1869-1878.

［9］SARTENAER T，DELOGNE P.Deterministic modeling of the（shielded） outdoor power line channel based on the multiconductor transmission line equations［J］.IEEE Journal on Selected Areas in Communications，2006，24（7）：1277-1291.

［10］AMIRSHAHI P，KAVEHRAD M.High-frequency characteristics of overhead multiconductor power line for broadband communications［J］.IEEE Journal on Selected Areas in Communications，2006，24（7）：1292-1303.

［11］ZIMMERMANN M，DOSTERT K.A multi-path signal propagation model for the power line channel in the high frequency range［C］∥Proceedings of 3rd International Symposium on Power Line Communications and Its Applications.Lancaster，UK：［s.n.］，1999：45-51.

［12］LIU Siqian，GOU Bei，LI Hongxiang，et al.Power-line communication channel characteristics under transient model［J］.IEEE Transactions on Power Delivery，2014，29（4）：1701-1707.

［13］RABIE K M，ALSUSA E.Effective noise cancellation using single-carrier FDMA transmission in power-line channels［J］.IEEE Transactions on Power Delivery，2014，29（5）：2110-2117.

［14］GIANAROLI F，PANCALDI F，VITETTA G M.The impact of statisticalnoise modeling on the error-rate performance of OFDM power-line communications［J］.IEEE Transactions on Power Delivery，2014，29（6）：2622-2630.

［15］MILIOUDIS A N，SYRANIDIS K N，ANDREOU G T，et al.Modeling of medium-voltage power-line communication systems noise levels［J］.IEEE Transactions on Power Delivery，2013，28（4）：2004-2012.

［16］ALSUSA E，RABIE K M.Dynamic peak-based threshold estimation method for mitigating impulsive noise in power-line communication systems［J］.IEEE Transactions on Power Delivery，2013，28（4）：2201-2208.

［17］ANKIT D，MALLIK R K，SCHOBER R.Performance analysis of a multi-hop power line communication system over log-normal fading in presence of impulsive noise［J］.IET Communications，2015，9（1）：1-9.

［18］TLICH M，ZEDDAM A，MOULIN F，etal.Indoorpower-line communications channel characterization up to 100 MHz-partⅡ：time-frequency analysis［J］.IEEE Transactions on Power Delivery，2008，23（3）：1402-1409.

［19］ANTONIALI M，TONELLO A M，LENARDON M，et al.Measurements and analysis of PLC channels in a cruise ship［C］∥IEEE International Symposium on Power Line Communications and Its Applications.St Louis，Missouri，USA：IEEE，2011：102-107.

［20］GOTZ M，RAPP M，DOSTERT K.Power line channel characteristics and their effect on communication system design ［J］.IEEE Communications Magazine，2004，42（4）：78-86.

［21］DUBEY A，MALLIK R K，SCHOBER R.Performance analysis ofa powerlinecommunication system employing selection combining in correlated log-normalchannelsand impulsive noise［J］.IET Communications，2014，8（7）：1072-1082.

［22］樊昌信，曹丽娜.通信原理［M］.北京：国防工业出版社，2007.

［23］VEDDER J D，何克明.误差函数及其反函数的简单近似［J］.物理实验，1989，9（3）：114-115.

［24］HOOIJEN O G.A channel model for the residential power circuit used as a digital communications medium ［J］.IEEE Transactions on Electromagnetic Compatibility，1998，40（4）：331-336.

［25］HOOIJEN O G，VINCK A J H.On the channel capacity of a European-style residential power circuit［C］∥IEEE International Symposium on Power Line Communications and Its Applications.St Louis，Missouri，USA：IEEE，1998：31-44.